考虑不平衡力与扰动力的深沟球轴承动力学模型

欧旭鹏，张义民，张 凯，王一冰

（沈阳化工大学装备可靠性研究所，辽宁 沈阳 110142）

1 前言

滚动轴承作为旋转机械的一个重要组成部分，对整个系统的运行起着决定性的作用。为了更加准确了解轴承的运行状态，通常建立滚动轴承动力学模型。动力学模型不但可以分析轴承的载荷和转速随时间变化的工作状态，并且可以更好的描述轴承动态响应特征。建立准确地动力学模型，可以进一步了解轴承在运行过程中的接触振动机理[1]。

最早，文献[2]考虑了轴系和支承结构的弹性变形，提出了故障轴承拟静力学分析方法；文献[3]对实际润滑的球型分离器和球的运动进行了全面的综合分析。文献[4]对轴承运转过程中的振动进行研究。研究表明了，轴承运行噪声和不稳定运行的最根本原因是变柔度振动；文献[5]提出了新的动力学模型，模型中考虑了轴承各元件尺寸变化、滚道曲率等因素；文献[6]考虑了轴承装配误差以及径向间隙的影响，分析了转速变化对轴承振动的关系；文献[7]以Hertzian接触变形理论为基础，建立了2自由度缺陷动力学模型，来模拟内、外圈单点缺陷，研究了局部故障下的动态特性；文献[8]建立了深沟球轴承内圈和外圈表面局部故障的2自由度动力学模型，分别得到了内、外圈表面单故障的深沟球轴承的振动响应；文献[9]考虑了表面粗糙度对滚道缺陷的径向加载双列轴承准静态载荷分布和刚度的影响，建立了2自由度的动力模型。

以上研究学者们从不同研究方向建立动力学模型。然而，不平衡力与扰动力对轴承的影响在动力学模型中却鲜见研究，为了更加准确地揭示振动响应的机理，考虑了轴承受到不平衡力与运行产生的扰动力的影响，并且在建立模型时考虑了轴承产生共振部分，建立轴系−内圈−外圈−轴承座四自由度传递深沟球轴承振动的解析模型。

对深沟球SKF6205 −RS为研究对象建立模型，采用四阶变步长的Runge −Kutta法对动力学方程式进行求解，得到了振动响应时域信号以及频域信号，并对结果进行了细化傅里叶处理，最后与西储大学轴承实验结果进行了比较，验证了模型的正确性和可靠性。

2 深沟球轴承动力学模型的建立

2.1 简化模型

深沟球轴承非线性动力学模型简图，如图1 所示。基于Hertzian接触理论，建立滚动轴承动力学模型。在建立模型时，进行如下假设：滚动体是等距均匀分布在内圈且进行纯滚动运动；不考虑润滑、油膜作用；忽略滚动体惯性效应、陀螺运动以及热效应引起的零件变形的影响等。

图1 深沟球轴承模型简化Fig.1 Simplified Model of Deep Groove Ball Bearing

2.2 接触刚度

Hertzian总接触刚度kn，是由滚道的接触几何形状决定的，总载荷—位移等效系数由滚动体与内圈和外圈的接触等效刚度kni，kno综合求得［10］。

2.3 径向变形

设x轴正方向与x轴正方向上方θio(t)的第一个滚珠夹角为θo，第i个滚子经过t时间后转过的角度为θi，即：

式中：x(t)、y(t)—内外圈的相对位移量；

Cr—径向间隙。

2.4 Hertzian接触力

轴承的内外圈滚道与球滚动体之间的接触形式为点接触。根据Hertzian接触理论，非线性载荷−位移关系为：

式中：Hi(t)—判断滚动体与滚道是否接触的参数。

如今，驾驶人也可跨省缴纳交通罚款啦。除了营业网点外，还可以通过手机银行等线上渠道付款。符合条件的，当事人还可以委托他人代处理。

2.5 阻尼力

对阻尼采用不同的计算方法：轴承接触阻尼的主要来源是滚动轴承与内外滚道之间存在的润滑膜，第i个滚子的接触阻尼力可以表示为：

2.6 不平衡力

轴承运行时的不平衡力受力分析，如图2所示。

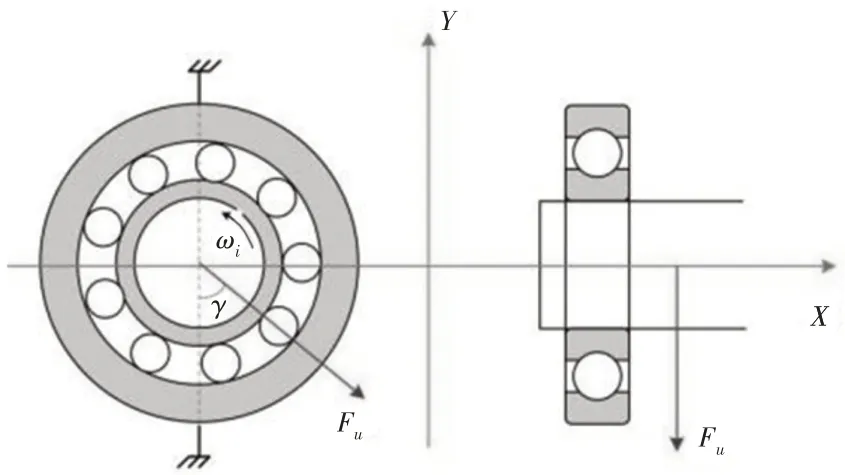
图2 不平衡力受力分析Fig.2 Force Analysis of Unbalanced Force

滚动轴承受到转轴不平衡力将产生受迫振动，其振动频率为转轴的旋转频率，产生的不平衡力为：

2.7 扰动力

在轴承运行时，由于承载滚子数在变化，导致内圈会受到轴系产生较小的扰动力，扰动力为：

式中：Nc—承载滚子数（不是总滚子数）；

F—细小扰动力；

ωb—滚子自转角速度。

3 动力学方程的建立

根据前面简化的轴承系统模型，在建立模型时，考虑了不平衡力以及扰动力，以及轴系—内圈，外圈—轴承座的非线性耦合关系。以X轴、Y轴为横纵坐标，轴承内外圈在4个方向建立了4自由度的动力学方程，如式（12）所示。

式中：mi—轴承内圈及轴系的等效质量；

mo—轴承外圈的等效质量；

kox、koy—轴承与轴承座之间的支撑刚度；

kix、kiy—轴承轴系之间的刚度；

cox、coy—轴承轴承座之间的支撑阻尼；

cix、ciy—轴承与轴系之间的阻尼。

4 数值计算及实验验证

4.1 数值模拟

对SKF6205−RS深沟球轴承为研究对象进行模拟验证。采用4阶Runge−Kutta对式（12）进行求解，获得深沟球轴承的振动响应结果。其中步长为1∕12000s，位移初始值为1×10−6m，速度初始值为0m∕s，外载荷为Wx=550N，Wy=650N，SKF6025−RS 轴承参数以及运行参数，如表1所示。

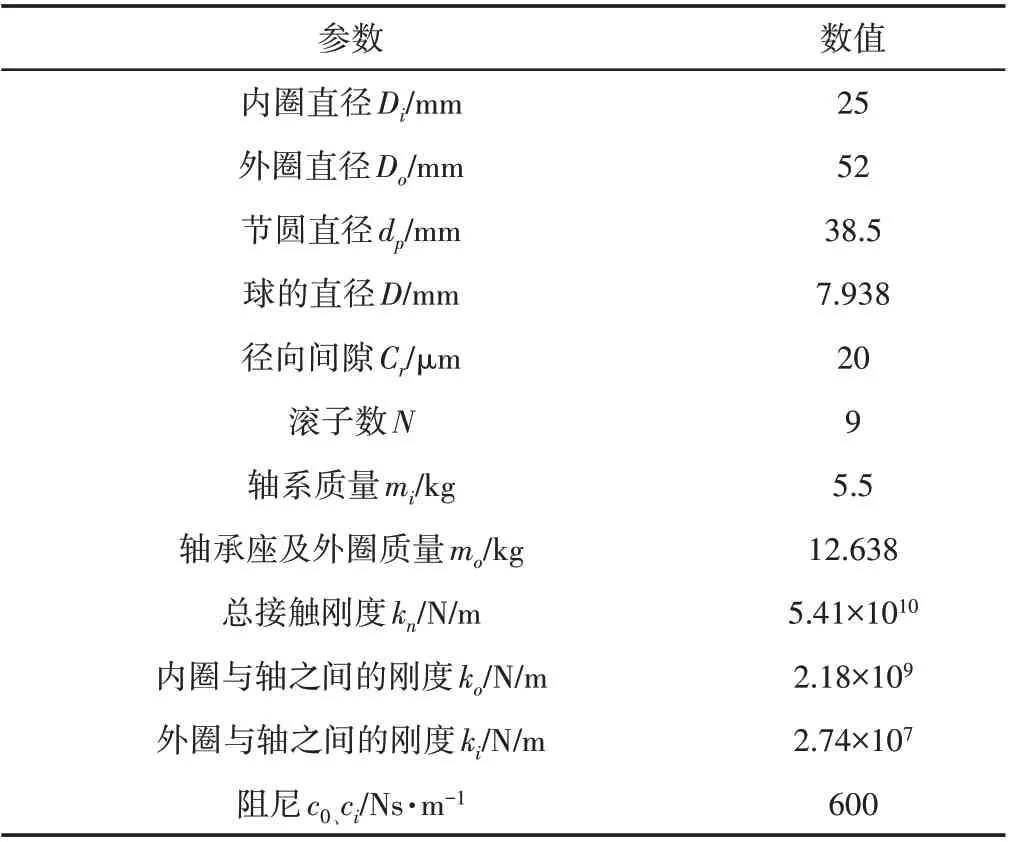
表1 SKF6025-RS轴承参数以及运行参数Tab.1 SKF6025-RS Bearing Parameters and Operating Parameters

动力学方程模拟得到的时域图，如图3（a）所示。由于初值原因在前期有一定幅值的冲击；时域信号快速傅里叶变化得到的频域图，如图3（b）所示。可以看出共振频率分别为1065Hz，2102Hz，（0～350）Hz的细化傅里叶变化得到的频谱图，如图3（c）所示。

图3 数值模拟结果Fig.3 Numerical Simulation Results

其中，29.17Hz 为转轴频率，58.59Hz 为二倍转频频率，104.7Hz 为滚动体通过外圈的频率，208.7Hz 为二倍频；158.2Hz为滚动体通过内圈的频率，315.7Hz为二倍频；262.2Hz为滚动体通过外圈频率和通过内圈频率之和，30.75Hz为转轴不平衡力激励的转频，68.85Hz为细小扰动力激励的频率。

4.2 实验及结果分析

试验轴承选取了SKF6205 −2RS深沟球轴承，试验采样频率为12kHz。轴承详细参数，如表1所示。转速在1750rpm下的时域图，由于运行环境、轴承自身运行中噪声以及其它力的影响，时域信号中有轻微冲击，如图4（a）所示。该转速下的频域图，如图4（b）所示。由于滚动轴承的通过频率都在低频段，中频段反应出轴承或结构零件的共振频率成分，因此选取了中、低频段，在图4（b）中，中频段（1～2.5）kHz 中有两个明显突起，分别是1065Hz、2102Hz，这与数值模拟傅里叶变化以后的图4（b）中1065Hz 和2100Hz左右的凸起很接近，这说明了本文的模型在考虑共振部分的因素是很有必要的。对（0～350）Hz采用细化FFT，细化FFT以后的频谱图，如图4（c）所示。从图中可以看出几个重要的旋转频率和通过频率，不平衡力激励频率为30.03Hz，与仿真结果是相一致的，68.12Hz为扰动力激励频率，与仿真结果是一致的，外圈通过频率为104.6Hz，内圈通过频率157.1Hz 等，希尔伯特调解图，如图4（d）所示。

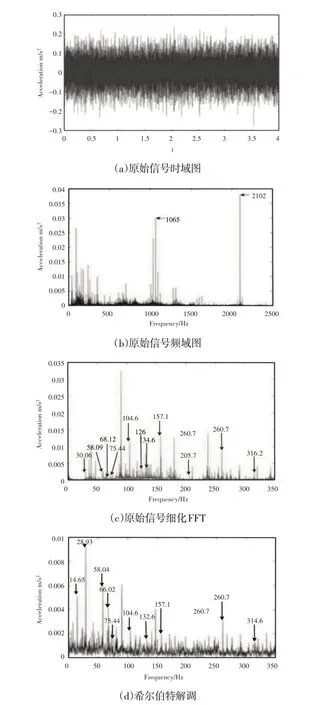
图4 转速1750rpm的实验结果Fig.4 Experimental Results with a Rotation Speed of 1750rpm

经过对振动信号希尔伯特解调以后，可以清晰地观察到轴承运行过程中的旋转频率和通过频率。转频为28.93Hz，跟理论值29.11Hz有点误差，这是由于转轴产生的不平衡力的原因；58.09Hz为二倍频，与理论值58.33Hz是基本吻合的；图中，1∕2fi为14.65Hz，这是轴回振动，可能是由于润滑不良引起的。

4.3 共振带频域分析

在建立模型时，考虑了中频段的共振因素。将模拟结果与试验结果结合分析。模型中其他参数不变，（1）改变Hertzian 接触刚度kn的值，代入系统模型方程中，kn= 3.0 × 1010，kn= 6.0 ×1010的频域图，如图5（a）、图5（b）所示。

结果发现改变kn时，1065Hz左右的共振频率，会发生变化，这就说明实验中1065Hz处的共振频率就是由轴承内部的刚度引起的；（2）改变轴承与轴承座之间的刚度kox的值，kox= 9 × 108的频域图，如图5（c）、图5（d）所示。

图5 改变参数的频域图Fig.5 Frequency Domain Diagram of Changing Parameters

2102Hz 左右的共振频率，会发生变化，说明实验中的2102Hz处的共振是由轴承与轴承座之间的刚度引起的共振。上述研究结果表明，提出的模型的主要贡献是获得的加速度频谱与实验测量所得的加速度频谱基本相一致。

模型真实模拟轴承共振现象，且模拟与试验频谱中的共振频率是一致的。结果证明，在一定的误差范围之内，提出的模型具有正确性和准确性的。

5 结论

本研究考虑了内圈受到轴系不平衡力以及扰动力的影响，建立4自由度深沟球轴承动力学模型。通过所建模型及实验对比结果表明，不平衡力及扰动力激励频率相一致，中频段的共振频率也是相一致的。通过定量分析得到试验中频段频率1065Hz是由Hertzian接触刚度引起的，2102Hz是由轴承外圈与轴承座的支撑刚度引起的。通过数值模型仿真与实验测试结果对比，结果吻合度较好，说明该模型的准确性和可靠性较好。