潜孔式弧门不同开度泄流时支臂稳定性分析

余星睿，杨光明，刘 良

(1.河海大学能源与电气学院，江苏南京211100；2.中水淮河规划设计研究有限公司，安徽合肥230601)

0 引 言

弧形闸门支臂属于大跨薄壁结构，这类结构的极限承载力主要取决于结构的稳定承载能力，结构的稳定性分析方法主要有特征值屈曲和非线性屈曲分析，因此对支臂结构进行屈曲分析很有必要。特征值屈曲分析能够快速、简单地求解出理想化弹性结构的临界屈曲荷载和屈曲模态，其屈曲模态亦可作为非线性屈曲分析时施加的初始缺陷[1]。弧形闸门支臂在实际制造、安装、运行等方面会产生初始缺陷，对支臂进行含初始缺陷的非线性屈曲分析，可更好地衡量结构的失稳特性。

针对闸门支臂的稳定性问题，国内部分学者进行了较多的研究。章继光等[2]考虑材料弹塑性影响，基于屈曲挠角法理论研究了弧门支臂空间屈曲荷载的求解方法及影响因素。曹青等[3]运用屈曲问题的有限单元法，采用NASTRAN软件对弧门支臂的屈曲荷载影响因素进行了探讨。丁峰等[4]等结合工程实例，利用ANSYS对弧门支臂进行特征值屈曲分析，研究了支臂夹角，支臂臂杆、立柱、斜撑杆等截面尺寸参数对屈曲临界荷载的影响。

综合分析国内外各类弧形闸门事故，可以发现大多都是因弧形闸门开启泄流时支臂失稳从而导致破坏，因此对闸门开启泄流时的支臂稳定性进行研究具有重要的理论价值和现实意义[5]。本文结合工程实例，采用ANSYS对不同开度泄流工况下的闸门支臂进行特征值屈曲分析，并首次考虑支臂的初始缺陷进行非线性屈曲分析，为实际工况下闸门运行稳定性数值模拟分析提供了借鉴。

1 结构稳定性分析控制方程

根据势能驻值原理，可得结构在平衡状态下的方程[6]

([KE]+[KG]){U}={P}

(1)

式中，[KE]为结构弹性刚度矩阵；[KG]为结构几何刚度矩阵；{U}为节点位移向量；{P}为节点载荷向量。

上式也可作为几何非线性稳定分析平衡方程，为得到随遇平衡状态，系统势能的二阶变分应为0，有

([KE]+[KG]){δU}=0

(2)

因此有

([KE]+[KG])=0

(3)

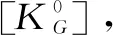
(4)

写成特征值的形式为

([KE]+λi[KG]){φi}=0

(5)

式中，λi为第i阶的特征值；{φi}为λi的特征向量，是该阶临界屈曲荷载下结构的失稳模态，各阶临界屈曲荷载为λi[P0]

2 支臂特征值屈曲分析

2.1 工程实例

某溢洪道工作闸门为双主横梁斜支臂圆柱铰潜孔弧形钢闸门，闸门尺寸为9.86 m×8.202 m，设计水头26.1 m，闸门底槛高程263.42 m，支铰中心高程270.43 m。支臂结构主要由上、下支臂，支臂腹杆和斜撑杆组成，各构件焊接相连，形成稳固的A 字形整体，闸门支臂结构三维模型如图1所示。其中上、下支臂采用箱型截面组合梁，支臂腹杆和斜撑杆分别采用36b号和20a号槽钢。

图1 弧形闸门支臂结构三维模型

2.2 支臂特征值屈曲求解流程

(1)建立支臂有限元模型。单独构造闸门支臂结构模型，支臂整体所用材料为Q235A钢，材料密度为7 850 kg/m3，弹性模量E=2.06×105MPa，泊松比υ=0.3。采用壳单元Shell181对支臂进行划分，划分得到单元73 234个，节点416 876个，生成支臂有限元模型如图2所示。

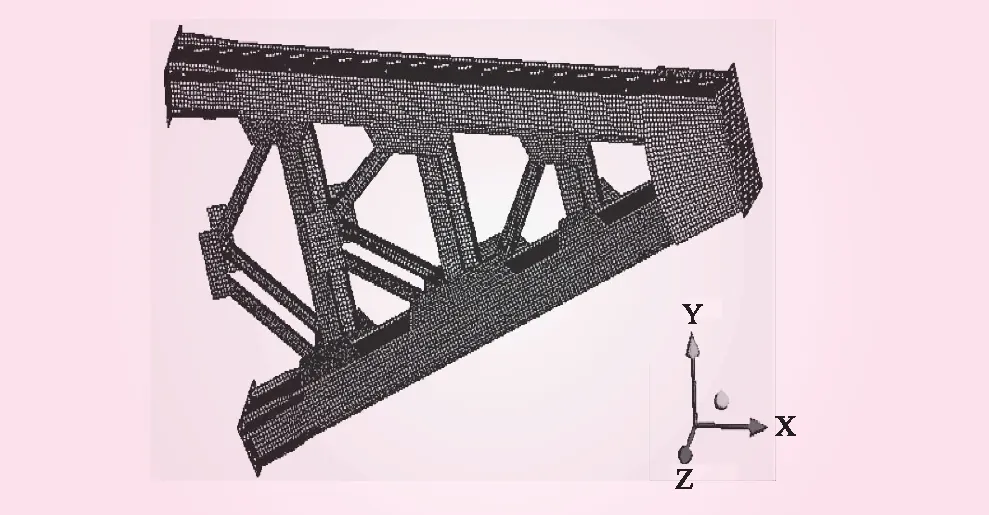
图2 弧形闸门支臂有限元模型

(2)施加约束和荷载。具体施加方式：支臂后端连接板位置沿x、y、z方向位移均为0，绕x、y方向转动约束为0；上、下支臂前端连接板沿y、z方向的位移为0。在水压力作用下支臂承受轴向荷载，轴力方向沿支臂轴线指向支铰中心，不同开启工况对应的轴向荷载不同。本文选取闸门开度(指闸门某一开启角度和全开启角度的比值)为0(开启瞬间)、0.05、0.1、0.2、0.3、0.45、0.6、0.8共8种开启工况对上、下支臂进行荷载计算，所得各开度上、下支臂轴向荷载分别为3 203.7、4 271.3、2 665.7、2 819.1、1 949.7、2 460.4、1 500.4、2 417.8、1 111、2 365.7、1 637.4、2 237.3、1 219.4、1 237、1 082.3、1 061.6 kN，然后根据荷载值进行不同开度下支臂特征值屈曲分析。

(3)设置求解选项并计算。首先设置静力学计算选项，然后将静力学分析模块与屈曲分析模块耦合，激活屈曲分析预应力选项，提取的特征值取前6阶，并指定前6阶对应的扩展模态，以便提取支臂结构的临界屈曲荷载和屈曲模态特征。

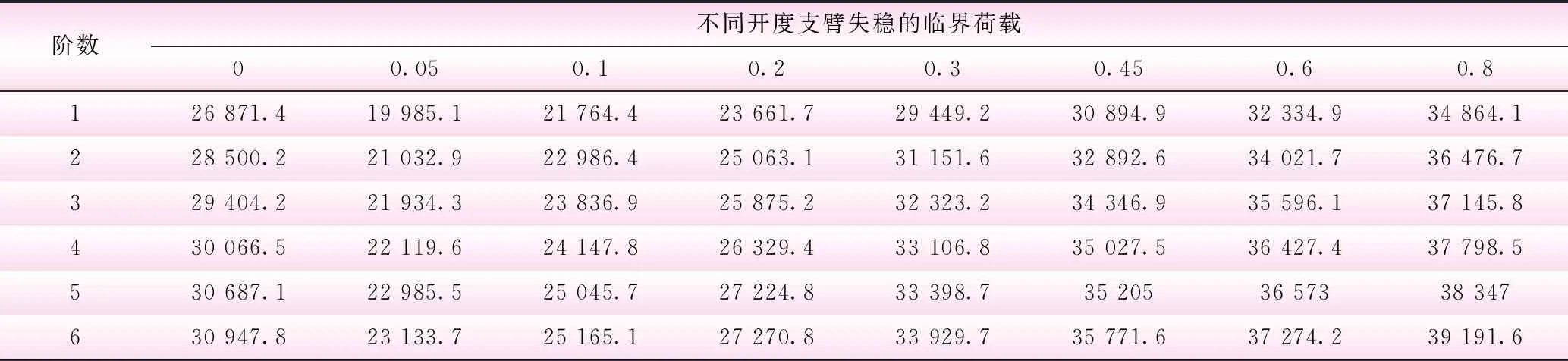
表1 各开度下支臂失稳的临界荷载 kN

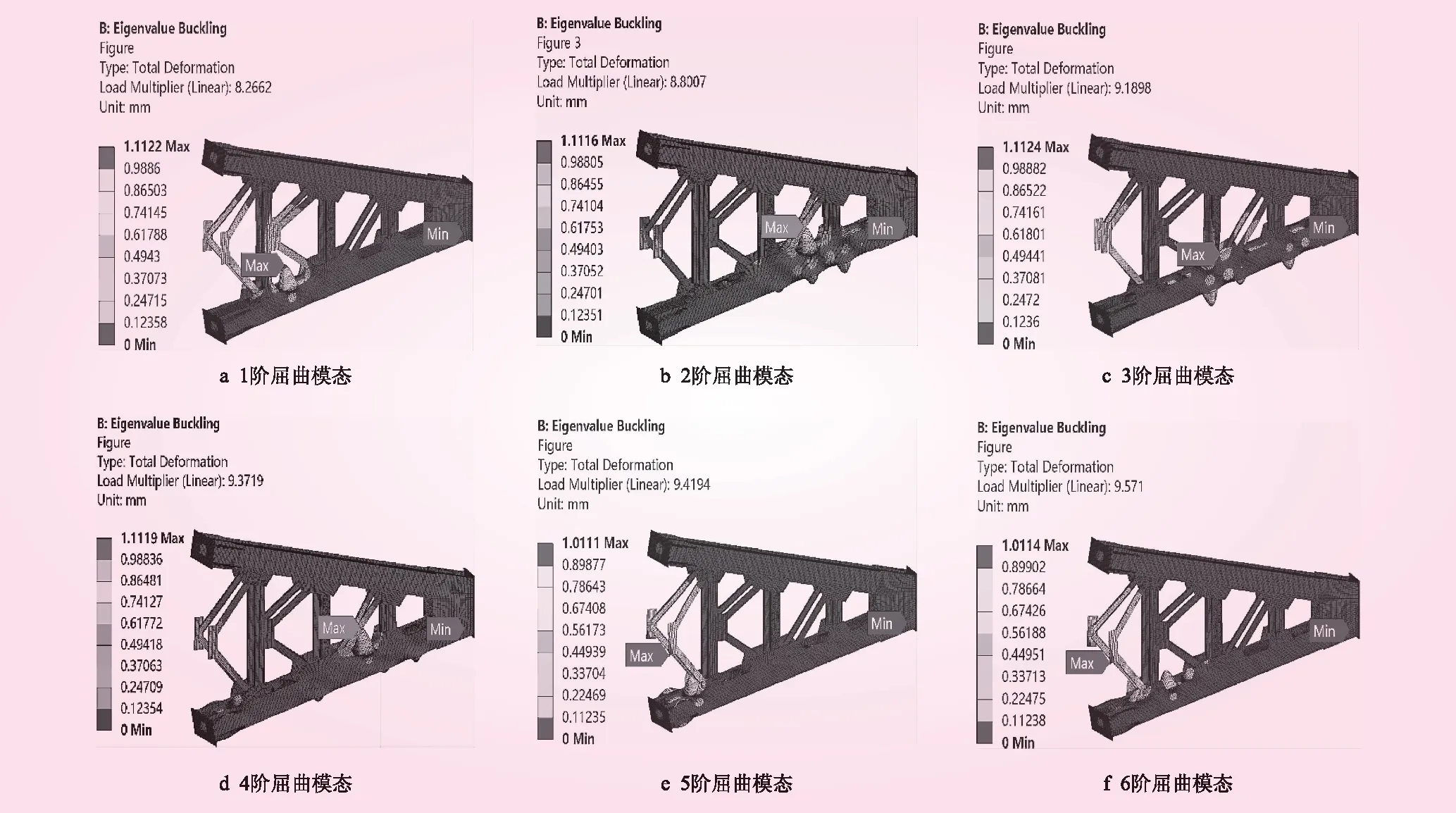
图4 闸门开启瞬间支臂前6阶屈曲模态云图

2.3 支臂特征值屈曲计算结果分析

通过ANSYS计算可以得到各开度工况下支臂失稳的临界荷载与对应的失稳模态，整理各开度下支臂前6阶临界屈曲荷载结果列于表1中，图3为各开度工况下支臂各阶临界屈曲荷载变化曲线。

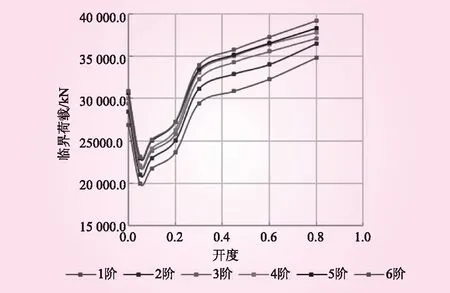
图3 不同开度下支臂各阶临界屈曲荷载变化曲线

闸门支臂在开启瞬间和开度为0.05时的前6阶屈曲模态如图4、5所示。

由表1和图3～5可知：

(1)闸门支臂各阶屈曲荷载随开度增大呈非线性变化，变化趋势接近一致。

(2)闸门开度在0～0.05范围内，各阶临界屈曲荷载随着开度的增大而迅速减小，在开度为0.05时，各阶临界屈曲荷载最小，支臂在承受19 985.1 kN轴向荷载时发生失稳，失稳模态表现为1、2号(支臂腹杆从前端至支铰依次编号1～3)腹杆之间的下支臂腹板出现纵波，最大变形为1.11 mm，需避免闸门在小开度停留以防止失稳；随着闸门的继续开启，各阶临界失稳荷载在0.05～0.3开度时发生了较为明显的增大，呈现加速增长的趋势，而在0.3～0.8时，各阶临界失稳荷载接近线性增长。

图5 闸门开度为0.05时支臂前6阶屈曲模态云图

(3)综合各开度下施加于支臂前端的荷载分析可知，上、下支臂承受相近大小荷载时与承受不等荷载时相比，支臂整体屈曲荷载更小。该闸门在局部开启时，下支臂所受轴向力往往比上支臂所受轴向力大，且按现行规范[7]计算可知，弧门全关挡水时支臂所受的轴向力约为10 183 kN，远小于最小临界屈曲荷载19 985.1 kN，均说明支臂结构布置形式较为合理。

(4)结合各开度下的屈曲模态可知(由于篇幅所限，仅列出闸门开启瞬间和开度为0.05时的支臂前6阶屈曲模态)，闸门运行开度对支臂各阶失稳模态几乎没有影响，不同开度下支臂各阶失稳模态形式接近一致，支臂的低阶屈曲模态主要表现为下支臂腹板的局部失稳，随着阶数的增大，失稳位置转移至支臂前端斜撑杆，但失稳变形量几乎不随阶数增加而变化。

3 特征值屈曲临界荷载最小工况下支臂非线性屈曲分析

由上文可知，闸门在开度为0.05泄流时，支臂特征值屈曲临界荷载最小，相对其它开度最容易发生屈曲失稳，故对此开度工况下的支臂进行基于初始缺陷(本文把一阶特征值屈曲模态作为水压荷载作用下支臂的变形，亦即初始几何缺陷)的非线性屈曲分析。

3.1 支臂非线性屈曲求解流程

(1)构造初始几何缺陷，重构几何模型。采用一致缺陷模态法对支臂进行几何缺陷构造，结构按最低阶模态变形将处于势能最小状态，使结构受力产生最不利影响[8]。据此得出的极限失稳荷载来分析实际结构有准确的安全裕量。特征值屈曲分析时一阶屈曲形态为1、2号(支臂腹杆从前端至支铰依次编号1～3号)腹杆之间的下支臂腹板出现纵波，梁的非线性屈曲分析中的缺陷添加比例一般是L/500[9](L为两端约束间距)，支臂腹板长约10 000 mm，初始几何变形取20 mm。将特征值屈曲分析求解结果导入Mechanical APDL中，并调用upgeom.inp初始缺陷文件，更新模块后将结果导入Finite Element modeler，以重构几何模型。

(2)设置结构材料参数。将Finite Element modeler中支臂模型导入Static Structural，并在Engineering Data中设置非线性屈曲分析所需材料参数。支臂屈服强度为235 MPa，抗拉强度为400 MPa，剪切模量G=7.69×104MPa，弹性模量E=2.06×105MPa，泊松比υ=0.3。

(3)静态结构分析模块中设置求解。在新建Static Structural中重新设置约束条件和施加荷载，上、下支臂前端连接板施加y、z方向的位移约束，支铰端连接板施加固定约束；两支臂前端连接板施加轴向力荷载，轴向力要大于线性分析的临界屈曲荷载19 985.1 kN，确保支臂在该荷载下发生屈曲，故取25 000 kN。设置迭代时间及相应迭代子步，打开自动时间步，实现逐渐施加荷载增量至给定荷载，打开大位移效应开关和Stabilization稳定性分析，应用标准Newton-Raphson 迭代方法，确定非线性屈曲临界荷载值和屈曲模态。

3.2 支臂非线性屈曲计算结果分析

非线性屈曲分析不同于特征值屈曲分析，由于结构在一开始就发生挠曲变形，且变形随着荷载的增加而增加。通常认为，如果结构荷载-位移历程曲线中从某点开始发生较大的转折，与先前完全不一样，就发生了屈曲，此时的荷载为屈曲荷载[10]。通过Static Structural 模块的迭代计算，最终得出考虑初始几何缺陷的非线性屈曲分析的荷载-位移历程曲线如图6所示，支臂屈曲失稳模态如图7所示。

图6 非线性屈曲分析荷载-位移历程曲线

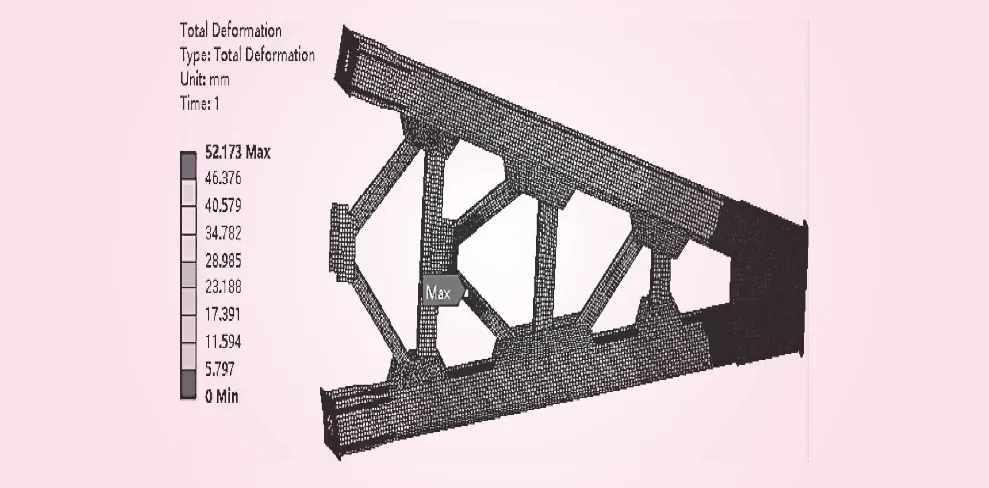
图7 非线性屈曲分析振型云图

由图6、7可知：

(1)支臂在承受16 630 kN的轴向荷载时，发生了屈曲失稳，该值小于对应的特征值屈曲临界荷载19 985.1 kN，说明支臂的初始几何缺陷会降低结构的稳定承载能力，对闸门的运行稳定性造成影响，故在闸门的制造、安装、运行过程中应注意避免支臂结构几何缺陷的产生，同时支臂稳定性分析时也应充分考虑结构的几何缺陷等非线性因素。

(2)非线性屈曲形态表现为支臂1、2号腹杆之间的下端斜撑杆发生失稳变形，失稳变形量为52.17 mm，与特征值屈曲失稳发生于下支臂腹板前端不同，非线性屈曲模态较符合实际工况下支臂发生局部失稳时变形产生的位置。在支臂1、2号腹杆之间的平行斜撑杆间增设加强板，并对加强后的支臂进行非线性屈曲分析。支臂的屈曲分析振型云图如8所示，由图8可知，与未设置加强板相比，支臂失稳变形量明显减小，为28.79 mm， 失稳发生位置由斜撑杆转移至支臂前端连接板，结果表明，在支臂两平行斜撑杆间增设加强板可有效提高支臂稳定性。

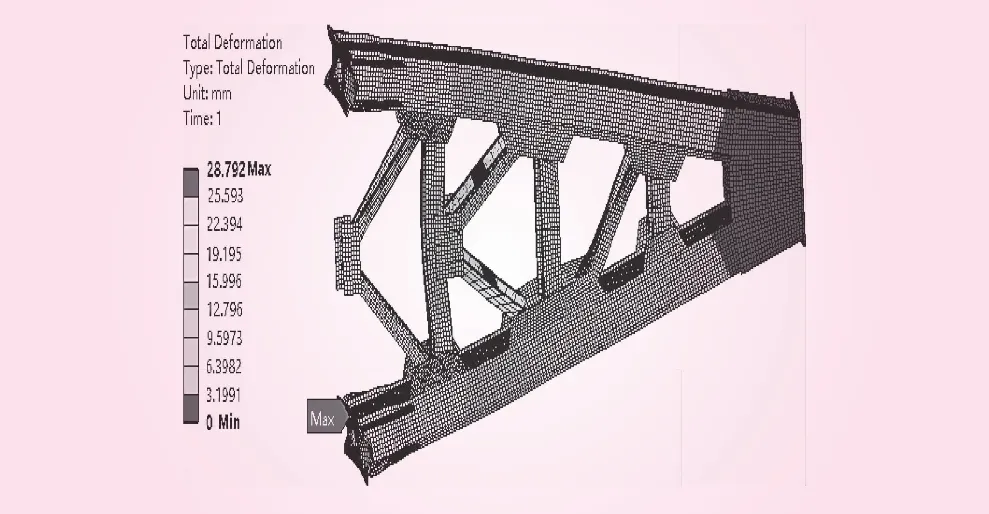
图8 加强后支臂屈曲分析振型云图

4 结 语

针对潜孔式弧门在不同开度运行工况下，对支臂进行稳定性分析，分别运用线性和非线性屈曲分析技术求解获得了支臂的屈曲临界荷载和屈曲模态。得出了以下几点结论：

(1)各开度下支臂各阶失稳模态接近一致，均发生于下支臂腹板或前端斜撑杆。

(2)支臂各阶特征值屈曲荷载随开度增大均呈现先减小后增大的趋势，闸门在开度为0.05时，支臂各阶临界屈曲荷载最小，一阶临界屈曲荷载为19 985.1 kN，屈曲模态表现为下支臂前端腹板出现局部失稳，需避免闸门在此开度停留以防止失稳。

(3)支臂的初始几何缺陷会降低结构的稳定承载能力，屈曲形态表现为支臂前端斜撑杆发生失稳变形，可在支臂两平行斜撑杆间增设加强板以提高支臂稳定性。