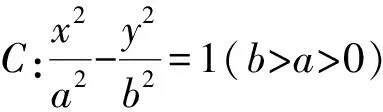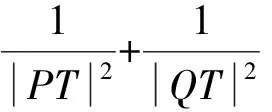利用极坐标简解两道期末解几试题

重庆实验外国语学校 (400039) 李小燕

极坐标与直角坐标相比，极坐标以极径与夹角为基本参数.在解决解析几何相关问题时，会更加便捷.本文以两道解析几何试题，探讨如何利用极坐标的思想进行求解.

一、试题展示

题1 (2021-2022学年上学期佛山市高二质量检测，16)已知圆C:(x-4)2+(y-2)2=4和点M(4,4)，若点N为圆C上一动点，点Q为平面上一点且∠MQN=90°，求点Q纵坐标的最大值.

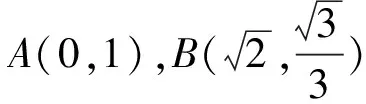
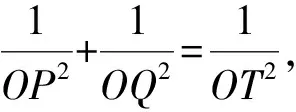
综上可知，上述两个问题均可转化为相关边长的范围.结合极坐标的特点，只要设计恰当地极坐标，即可高效的解决上述两个问题.

二、解法呈现

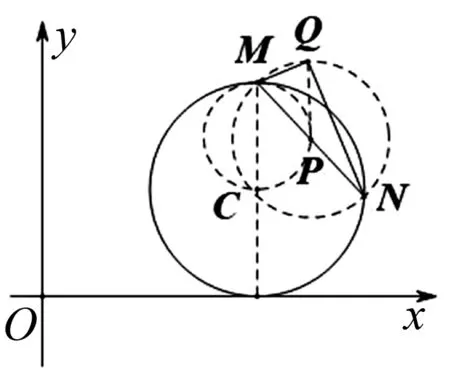
图1

关于题1，如图1，根据圆的垂径定理，可得CP⊥MN，从而可得点点P的轨迹是以CM为直径的圆P:(x-4)2+(y-3)2=1.

根据上述分析可知点Q纵坐标的最大值为yP+PM.为了方便计算，可构造一个新的图形对该问题进行转述.如图2，设点P的轨迹为K:x2+(y-1)2=1，以及直线l:y=4.试计算OP+dP-l的最大值.

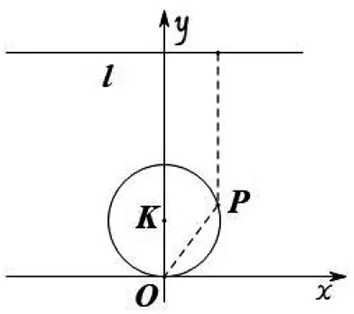
图2

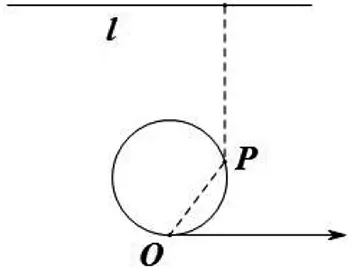
图3

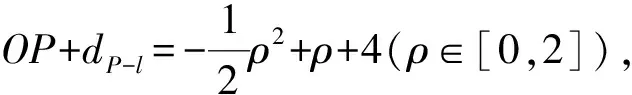
反思：利用极坐标进行求解，直击问题的本质，运算量低，且便于推广.当将直线l进行平行移动时，仅需将最终的最值进行相应的平移即可.

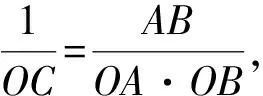
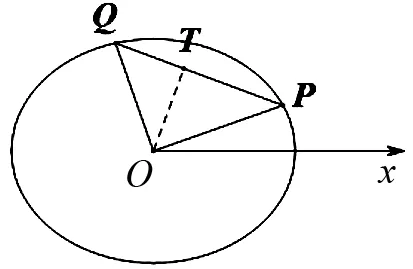
图4

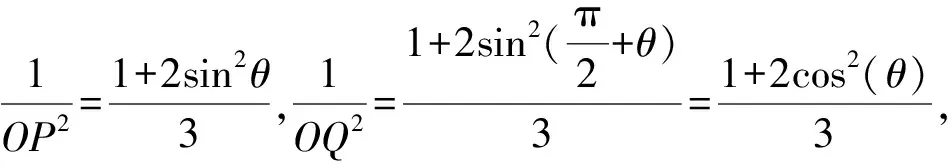
综上可知△OPQ的边PQ上的高为定值.

三、一般化结论

上述解法可将该结论推广至一般性的椭圆.

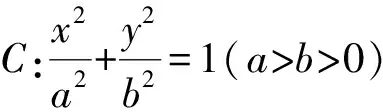
类比椭圆，也可将该结论推广至双曲线与抛物线.