例谈拉格朗日乘数法的初等化应用

江苏省梅村高级中学 (214112) 陶煜瑾

拉格朗日乘数法是高等数学中求多元函数条件极值的重要方法，方法程序性强，容易掌握.由于其涉及高等数学中的知识，不便于高中学生的理解，所以需将其进行初等化，变化其结构方便高中学生理解与操作.

1 拉格朗日函数的初等化

对于已知条件二元方程φ(x,y)=0，求目标函数f(x,y)的极值问题，我们可以先构造拉格朗日函数l(x,y,λ)=f(x,y)+λφ(x,y)，由于φ(x,y)=0，我们可以发现f(x,y)的极值即为l(x,y)的极值，且与λ无关.

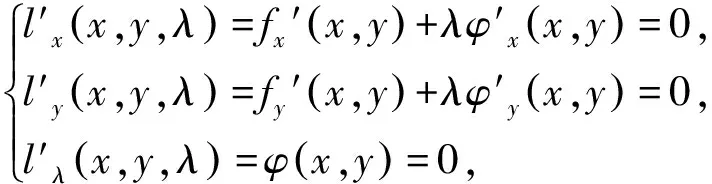
fy′(x,y)≠0，由此方程组可以找出目标函数的极值点.

2 拉格朗日乘数法求最值

2.1 整式型条件最值

例1 设x，y为实数，若4x2+y2+xy=1，求2x+y的最值.

解析：设f(x,y)=2x+y，φ(x,y)=4x2+y2+xy-1=0，由拉格朗日乘数法可知

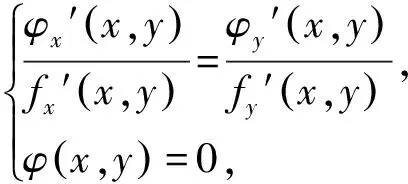
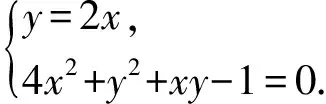
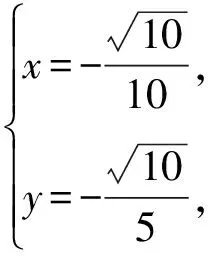
评注：运用拉格朗日乘数法求最值，其中条件方程与目标函数的最优形态为整式形式，此时求偏导最为方便.

2.2 分式型条件最值

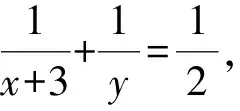
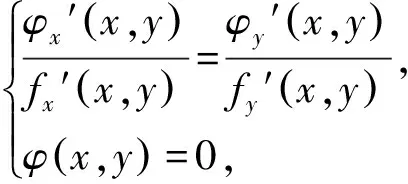
评注：运用拉格朗日乘数法求最值，其中条件方程为分式时，可以将条件化为整式，从而方便求偏导.

2.3 结构不良型条件最值

例3 设x，y为实数，且x2+xy+2y2=3，求x2-xy+2y2的最值.

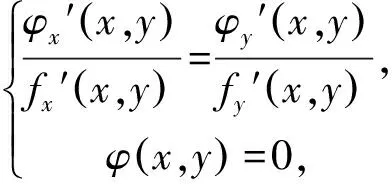
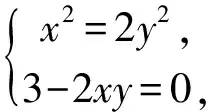
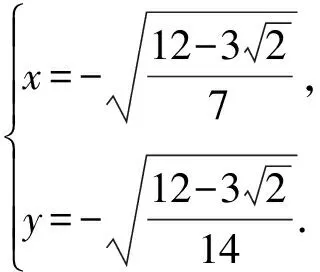
评注：运用拉格朗日乘数法求最值，其中目标函数比较复杂时可以利用条件方程简化目标函数，从而方便求偏导.

3 无极值条件最值

例4 设x，y为实数，且5x2+4y2=10x，求x2+y2的最大值.

解析：设f(x,y)=x2+y2，φ(x,y)=5x2+4y2-10x=0，由拉格朗日乘数法可知

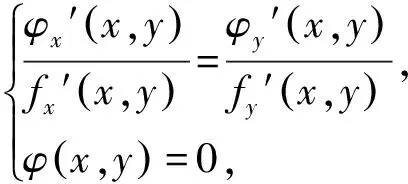
评析：运用拉格朗日乘数法求最值，若目标函数无极值，则不可以用拉格朗日乘数法求最值，此时需要用一般方法求之.

4 多元函数的最值

由二元拉格朗日乘数法可知，对于已知条件方程φ(x1,x2,…,xn)=0，求目标函数f(x1,x2,…,xn)的极值问题，我们可以先构造拉格朗日函数l(x1,x2,…,xn,λ)=f(x1,x2,…,xn)+λφ(x1,x2,…,xn)，由于φ(x1,x2,…,xn)=0，我们可以发现f(x1,x2,…,xn)的极值即为l(x1,x2,…,xn)的极值，且与λ无关.因为

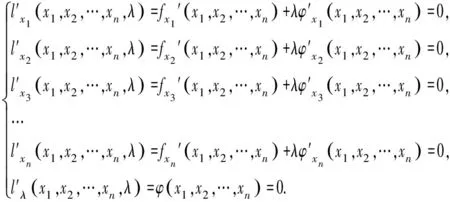
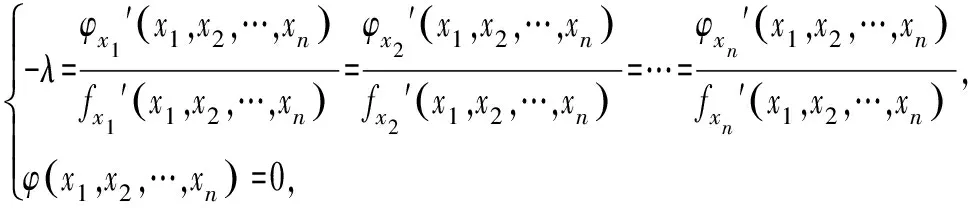
例5 设x，y为实数，且2x+2y+z=1，求3xy+yz+zx的最大值.

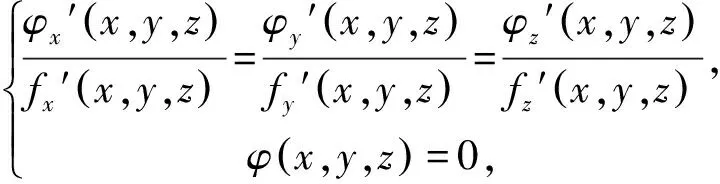
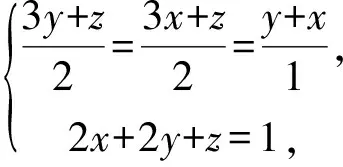
评注：对于三元及三元以上的带限制条件的最值，若目标函数有极值也可以用拉格朗日乘数法求最值.