借助三角形外心 巧妙求解参数值——对一道向量题的探究

⦿江苏省无锡市江阴长泾中学 刘旭东

平面向量同时兼备“数”的性质与“形”的特征，一直是历年高考数学试题中的热点题型之一.而在平面向量中融入三角形的基本特征，设置创新新颖，内涵丰富多彩，破解思维多变，是数学知识、数学思想方法和数学能力交汇与融合的一大主阵地，具有很好的选拔性与区分度，倍受各方关注.

1 问题呈现

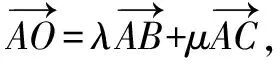
此题以三边长确定的三角形为问题背景，结合三角形的外心，通过含参的平面向量的线性关系式的设置，来确定对应的两参数的和.破解时，可以从平面向量角度、解三角形角度、坐标角度等切入，利用不同的方法来处理与求解.

2 问题破解

方法1：数量积转化法.

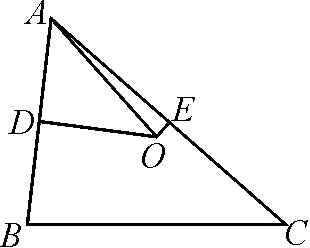
图1

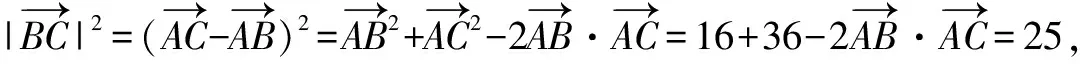
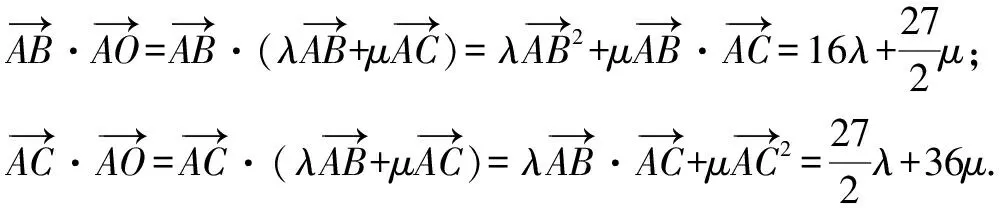
如图1,过外心O作OD⊥AB，OE⊥AC，垂足分别为D，E，则D，E分别为AB，AC的中点.

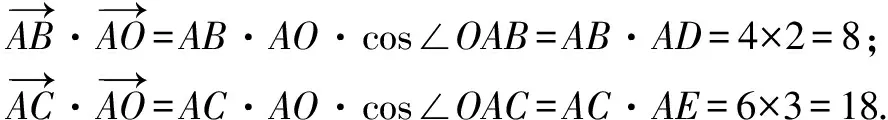
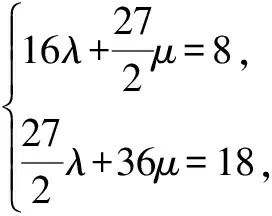
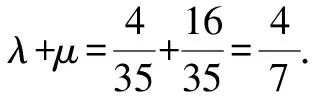
点评：结合平面几何的图形特征，通过辅助线的构建，借助三角形外心的实质，综合平面向量的数量积以及直角三角形的定义加以转化，建立两参数的方程组，利用方程组的解来确定相应的参数值，进而求解两参数的和.合理利用平面向量的线性关系，结合向量数量积公式的应用加以巧妙转化，这是破解此类平面向量计算问题的常见方法.

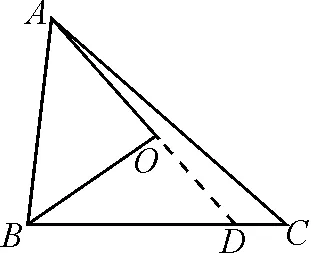
图2

方法2：解三角形法.

解析：如图2,延长AO交BC于点D.

根据余弦定理，可得

由同角三角函数基本关系式，得

在△OAB中，根据余弦定理，得

由同角三角函数基本关系式，得

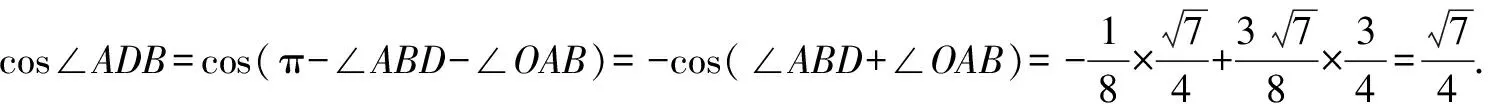
所以∠OAB=∠ADB，于是BD=AB=4.

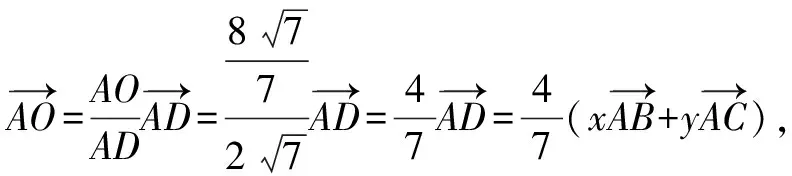
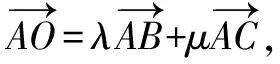
点评：结合三角形的几何背景，综合应用余弦定理与正弦定理、同角三角函数基本关系式、三角形的内角和、诱导公式以及三角恒等变形公式等，通过平面向量中三点共线的性质及其定理加以合理转化，进而求解两参数的和.合理利用解三角形与平面向量的综合知识，结合三角函数的相关知识加以巧妙转化，这是破解此类涉及三角形的平面向量问题的常见方法.

方法3：余弦定理的向量表示法.

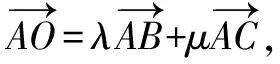
结合余弦定理的向量表示形式，由上式可得

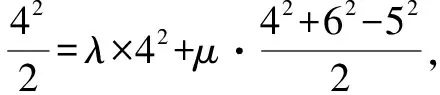
32λ+27μ=16.

①

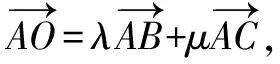
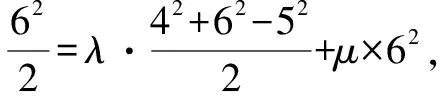
3λ+8μ=4.②

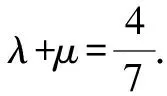
故选择答案：C.

点评：方法3是在方法1的基础上进一步优化而来，借助余弦定理的向量表示形式加以转化与应用，结合平面向量的数量积与余弦定理的应用来处理，合理转化，巧妙破解，进而得以求解两参数的和.合理利用余弦定理，是对平面向量与解三角形知识的有效融合与应用，可以更好优化过程，提升解题效益.

3 变式拓展

探究1：保留问题的所有条件，改变设问方式，分别求解两参数的对应值，得到以下对应的变式问题.

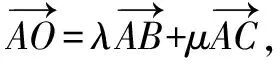
探究2：保留三角形外心的背景，改变问题的相关条件，给出平面向量的线性关系式，求解对应角的余弦值，得到以下对应的变式问题.

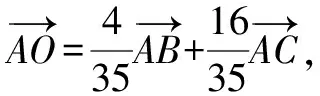
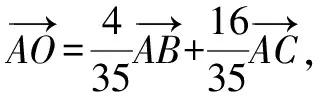
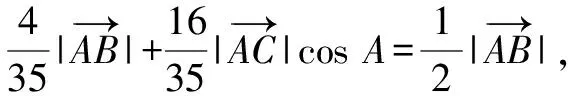
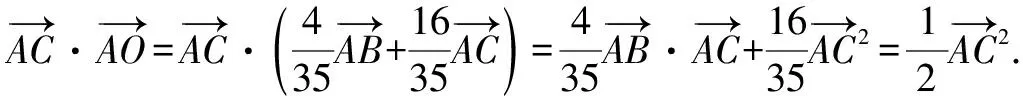
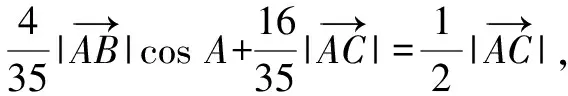
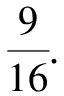
4 解后反思

破解此类巧妙融合三角形与平面向量相关知识的数学问题，关键是正确把握其中“数”的性质与“形”的特征.可以从“数”的性质入手，利用代数视角，通过代数运算或平面向量的运算等形式来解决；也可以从“形”的特征入手，利用几何直观，通过平面几何特征或图形直观等形式来处理；更高层次就是“数”与“形”的综合应用，两者协同合作，通过坐标运算等形式来破解等.破解思维各异，方法多样.