运用复数思维解决非复数类问题“五法”

⦿福建省厦门市第六中学 吴 瑾

1 引言

高中关于复数的系统学习，主要集中在人教版选修2-2第三章“数系的扩充与复数的引入”.复数思维是建立在复数知识之上的一种重要数学思维，它利用复数的代数式、三角式，模及其运算的几何意义，为我们解决代数、三角、几何等学科中的非复数问题提供了又一个思维方法和解题途径.

2 解决非复数问题“五法”

2.1 利用复数幂的周期性

根据代数式的对称性和排列组合数的规律性，我们可以将其转化为复数问题[1]，利用复数的性质进行求值或证明，从而达到快速解题的目的.

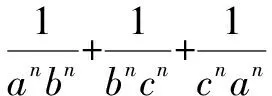
=1+ωn+(ω2)n

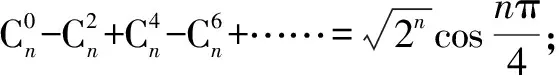
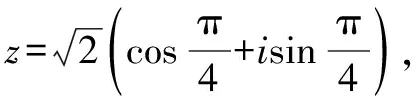
又根据二项式定理,得

方法与技巧：通过观察，发现题目中这些组合数的上标从0，1，2，3起，组合数的符号具有“+、+、-、-”的周期性，自然会联想到复数，进而利用复数的性质完成证明.本题主要运用了in的周期性及棣莫佛定理.

2.2 利用复数的模

利用复数模的不等式，能够为我们解决实数的有关问题提供模型，把诸如求函数值域、解(证明)不等式、求极值等问题转化为复数问题.这种间接的解题方法具有“化繁为简”的优越性.

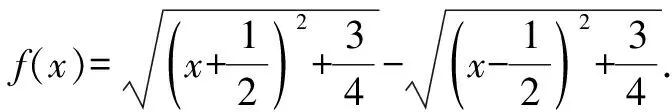
f(x)=|z1|-|z2|.

因为 ||z1|-|z2||≤|z1-z2|=1,

①

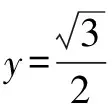
所以||z1|-|z2||<1.

故所求函数的值域为(-1,1).

方法与技巧：本题巧妙地利用了复数模的不等式，将函数问题转化为复数问题.从本题的求解过程可以发现以下规律，对于复数模的不等式||z1|-|z2||≤|z1±z2|≤|z1|+|z2|，当且仅当z1=kz2(k>0)时，|z1+z2|=|z1|+|z2|，|z1-z2|=|z1|-|z2|；当且仅当z1=kz2(k<0)时，|z1+z2|=||z1|-|z2||，|z1-z2|=|z1|+|z2|.

例4已知|a2-b2|+2|ab|=1(a，b∈R).

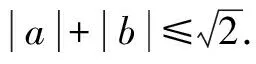
证明：设z=a+bi，则z2=a2-b2+2abi.于是 |Re(z2)|+|Im(z2)|=1.

因为对于任意复数z，总有

②

所以可得|z|2=|z2|≤|Re(z2)|+|Im(z2)|=1，即|z|≤1.

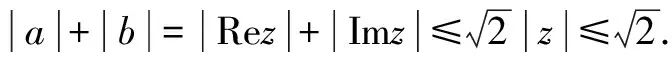
方法与技巧：本题是运用复数的模证明不等式的典型实例，其中②式揭示了复数的模与其实部、虚部绝对值之间的关系，把a2-b2与2ab看作复数(a+bi)2的实部与虚部也是解题常用的一种技巧.

2.3 利用复数积(商)的辐角

在求三角函数值的一些问题中，可以利用复数积的辐角等于两个复数的辐角之和，或者运用共轭复数的性质进行等价变形等方法来求解，这样既可以避免繁琐的计算，又容易找到解决问题的突破口.

所以原式=arg(3+i)+arg(5+i)+arg(7+i)+arg(8+i)

=2kπ+arg[(3+i)(5+i)(7+i)(8+i)]

方法与技巧：本题将反三角函数中的角转化为复数的辐角，进而利用复数积的辐角等于各复数辐角之和，充分体现了用复数思维解这类题的优越性.

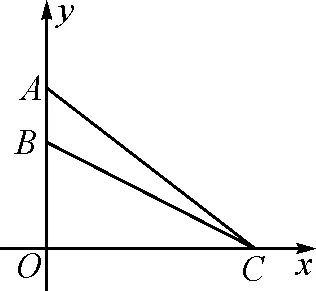
图1

例6如图1，在平面直角坐标系中，在y轴的正半轴(坐标原点除外)上给定两点A，B，试在x轴的正半轴(坐标原点除外)上求点C，使得∠ACB取得最大值.

解：以直角坐标系确定一个复平面，设A，B，C三点对应的复数为zA,zB,zC，则

zA=ai，zB=bi(00).

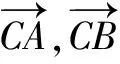
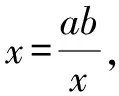
2.4 利用复数的n次方根

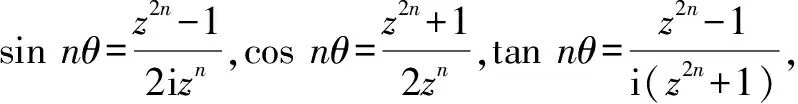
例7求tan 9°+cot 117°-tan 243°-cot 351°的值.

解：设z=cos 9°+isin 9°，则z10=i.

所以 tan9°-cot351°+cot117°-tan243°

=tan9°+cot9°-tan27°-cot27°

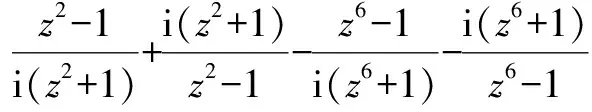
方法与技巧：本题先利用诱导公式，将诸角化为某一个角的倍数关系，以便应用棣莫佛定理的变形公式.由解题的过程可以看出，运用复数思维来步步化简的方法显得非常简洁明快.

证明：因为z7-1=(z-1)(z6+z5+z4+z3+z2+z+1)，又根据根的定义，有

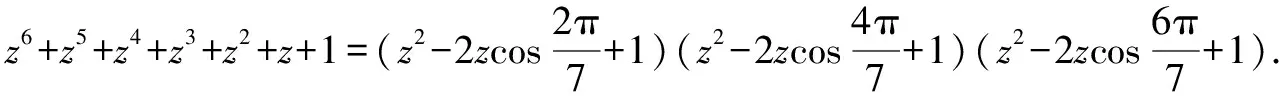
令z=1，得

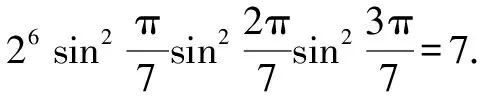
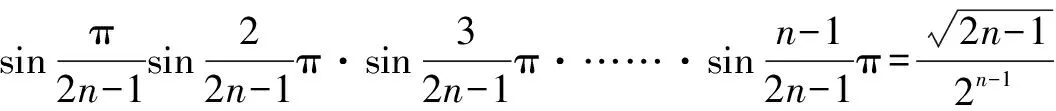
2.5 利用向量的旋转与共线

对于解析几何中涉及到的较复杂的特殊角的多边形类问题，如果利用复向量的旋转与共线的性质来解决会显得很简捷.

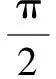
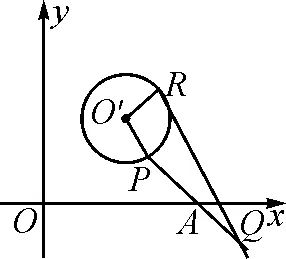
图2

解：如图2，根据直角坐标系确定一个复平面，设点P，Q，A对应的复数分别为zP，zQ，zA，根据点P，Q关于点A对称可知z→AP=z→QA.

即

zP-zA=zA-zQ.

③

又因为zA=9,所以zQ=18-zP.

因为z→O′P=zP-zO′=zP-(5+5i),所以z→O′R=z→O′P·i=zPi+(5-5i).

于是zR=z→O′R+zO′=zPi+(5-5i)+(5+5i)=zP·i+10.

z→QR=zR-zQ=(zP·i+10)-(18-zP)=(1+i)·zP-8=[zP-(5+5i)](1+i)+5(1+i)2-8=[zP-(5+5i)](1+i)-(8-10i).

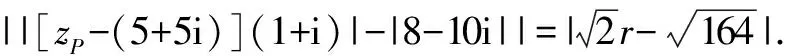
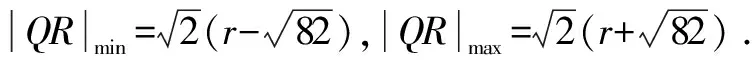
方法与技巧：本题中运用共线向量导出③式以便应用zA=9；将zP配凑成zP-(5+5i)以便取模得到半径，这些都是我们应当学习和掌握的解题技巧.

图3

例10如图3，∠MON=60°，边长为a的正三角形ABP在∠MON内滑动(不能翻转)，使点A始终在OM上，点B始终在ON上，求点P的轨迹方程.

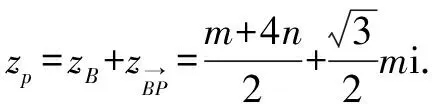
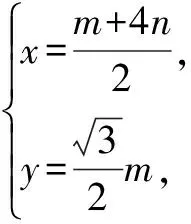
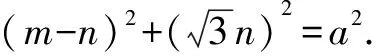
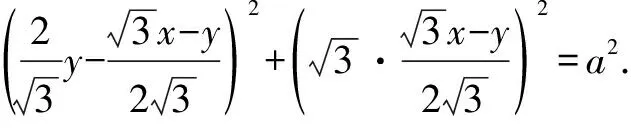
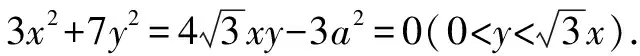
方法与技巧：本题是把求动点轨迹的问题转化为复数(复平面)问题来求解，除了运用复数思维，本题还体现了求轨迹问题的设参、消参等参数思想.

3 总结

从上述典型例题的解答中可以看到，运用复数思维解决非复数类问题的方法和技巧具有广泛性、实用性和极大的灵活性.我们应该通过多种练习，学习、领会和掌握这些方法与技巧，这有助于开阔我们的思路，不断提高综合解题能力.