图形优美 思维精妙——探究两条抛物线相切的问题

⦿甘肃省张家川县第一高级中学 李晓东

平时，我们经常遇到直线与抛物线相切的问题，也掌握了处理此类问题的常用方法.那么，当遇到一条抛物线与另一条抛物线相切时，该如何处理呢？实际上，可根据图形特征，转化为存在一条直线与两条抛物线均相切；亦可根据切点的唯一性，转化为相关方程有唯一解.下面结合一道试题的多解探究以及变式训练，领会解题思维，提升解题技能.

1 好题采撷

(2021年广东地区中科大强基测试第2题)设抛物线y=x2与x=ay2+1相切，则a=______.

分析:本题以两条抛物线相切为载体，具有一定的创新性，看似简单，实则内涵丰富；侧重考查学生的数形结合能力、转化能力、逻辑推理能力以及数学运算求解能力；有利于数学思想方法、知识在解题中的灵活运用，能够较好地培养学生的探索精神、创新意识，提升学生的数学核心素养.

图1

2 多解探究

如图1，在同一坐标系内分别画出抛物线y=x2与x=ay2+1(该抛物线显然恒过定点(1,0)).根据题意易知a>0.(先确定参数的取值范围，便于进一步分析.)

由图可知，在两条抛物线的公共点处，存在一条直线与两条抛物线均相切.

视角一：由于题设两条抛物线相切可转化为存在一条直线与两条抛物线均相切，又因为当直线与抛物线相切时，可考虑对应二次方程的判别式Δ=0在处理问题中的灵活运用，所以本题可充分利用“判别式为零”，并结合切点的坐标加以灵活分析.

①

②

点评：该解法的关键是充分利用直线与抛物线相切，根据Δ=0巧求切点的坐标，突出体现了“方程思想”在解题中的灵活运用，对运算求解能力的要求较高.

视角二：由于题设两条抛物线相切可转化为存在一条直线与两条抛物线均相切，又因当直线与抛物线相切时，可考虑导数的几何意义在分析、解决问题中的灵活运用，所以本题可充分利用导数的几何意义，并结合相关导数知识加以灵活分析.

解法2：依题意，对y=x2求导得y′=2x；对x=ay2+1求导得1=2ayy′.

点评：解法2的关键是充分利用导数的几何意义以及切点在抛物线上，构建等式.此外，要注意对x=ay2+1的求导，应灵活运用复合函数的求导法则.

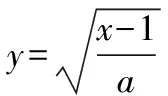
点评：解法3与解法2不同之处在于需要先转化题设条件，以便能够直接利用求导公式；同时要注意两条抛物线在切点处的切线斜率相等及导数几何意义的运用.

视角三：由于题设两条抛物线相切可转化为存在一条直线与两条抛物线均相切，又因当直线与抛物线相切时，可考虑对应二次方程的判别式Δ=0与导数的几何意义，所以本题可将“判别式为零”与“导数的几何意义”在解题中同时加以灵活运用.

③

④

点评：解法4的关键是综合运用了Δ=0和导数的几何意义，同时要注意直线方程点斜式的运用.显然，该解法对学生综合运用能力的考查较强，有利于较好地培养学生的运算求解能力.

视角四：考虑“等价转化思想”的灵活运用，可先将题设两条抛物线相切转化为关于x或者关于y的方程有唯一解，再结合其他知识加以灵活分析.

解法5：将y=x2代入x=ay2+1，可得

ax4=x-1.

⑤

依题意知方程⑤有唯一解，所以直线y=x-1与抛物线y=ax4必相切.

⑥

点评：解法5需要先将题设条件等价转化为方程有唯一解，再等价转化为直线与抛物线相切，最后借助导数知识和方程思想加以灵活求解.显然，该解法突出考查了学生灵活运用“等价转化思想”分析、解决目标问题的能力.

图2

点评：解法6需要先将题设条件等价转化为直线与函数的图象有唯一公共点，再借助导数知识以及数形结合思想加以灵活求解，有利于较好地培养学生的数学核心素养.

3 变式训练

⑦

说明：有兴趣的读者可参考前述例题的多种不同解法，给出本题的其他解法.

综上，处理两条抛物线相切的问题，有多种不同的解题视角以及对应的具体解法.需要我们特别关注的是：(1)要学会以图形的直观、明了性作为分析、解决问题的切入点，便于帮助我们迅速获得具体的解题思路；(2)要学会灵活运用“等价转化思想”，将不熟悉的数学问题等价转化为熟悉的数学问题，便于根据已掌握的知识、方法顺利求解；(3)通过试题的多解探究以及变式训练，努力提高直观想象、数学运算、数学抽象以及逻辑推理等数学核心素养，进而提高分析、解决此类问题的技能技巧.

4 结语

一言以蔽之，小题不小，蕴含丰富，具有较好的思维价值、探究价值，值得我们去细细品味、深思；有利于提高学生对所学相关数学知识和思想方法的综合运用能力，也有利于进一步拓宽视野，提高思维的灵活性、严谨性、逻辑性，进而提升理性思维能力.