非稳态Hamilton-Jacobi方程的7阶加权紧致非线性格式1)

胡迎港 蒋艳群 黄晓倩

(西南科技大学数理学院,四川绵阳 621010)

引言

d维空间下非稳态Hamilton-Jacobi (HJ)方程定义如下

其中,t>0 ,x=(x1,x2,···xd)T,这类方程在物理学、流体力学、图像处理、微分几何、金融数学、最优化控制理论等诸多领域中有着广泛应用[1-4].其解的性质很特殊,如弱解存在但不唯一,即使初值和Hamilton 函数充分光滑,方程解的导数也可能出现间断[5].Crandall 等[6]首次提出了HJ 方程的黏性解的概念,并证明了黏性解的存在唯一性.HJ 方程的性质与双曲守恒律方程十分相似,因此,可以将双曲守恒律方程的一些成熟数值方法[7-9]推广用于求解HJ 方程.

目前已有较多的高精度算法被推广应用于HJ 方程.如Osher 等[10]通过选择最光滑的候选模板重构数值通量方法设计了HJ 方程的二阶本质无振荡 (ENO) 格式.Jiang 等[11]通过将所有候选模板的重构通量进行了非线性加权得到了HJ 方程的5 阶加权本质无振荡 (WENO) 格式.相比于ENO 格式,WENO 格式在光滑区域能达到更高阶精度,同时在间断区域恢复为ENO 格式.Bryson等[12]设计了HJ 方程的5 阶中心加权本质无振荡(CWENO)格式.Qiu 等[13]提出了HJ 方程的基于Hermite 多项式的5 阶HWENO 格式,该格式在重构通量时具有更好的紧致性.Ha 等[14]为改善格式的间断捕捉能力,采用拉格朗日型指数多项式建立了一种新的6 阶WENO格式.相比于其他类型的WENO 格式,该格式具有更低的计算成本.Cheng 等[15]基于经典的5 阶WENO 格式,采用4 个二次多项式的非线性凸组合重构数值通量,提高了格式的精度 (在光滑区域能达到6 阶) 和健壮性.Zhu 等[16]基于原始的5 阶HWENO 格式,通过采用大小不同的候选模板构造了HJ 方程的更加简单有效的HWENO 格式.Rathan[17]提出了一种新的5 阶WENO 格式求解HJ 方程,该格式通过设计L1范数型的非线性权重来提高精度和分辨率.Abedian[18]采用对称的5 阶WENO 格式求解HJ 方程.Kim 等[19]基于指数多项式构造了一种新的3 阶WENO 格式.其特点是可以很好地分辨出光滑区域和间断区域.

高阶精度加权紧致非线性格式 (WCNS) 是另一种求解双曲守恒律方程的有效方法.Deng 等[20]基于WENO 格式的构造思想,在紧致非线性格式[21](CNS) 中引入非线性WENO 插值技术,提出了高阶精度WCNS 格式.该格式被证实具有高分辨率和强间断捕捉能力等良好特性.Nonomura 等[22]和Zhang 等[23]分别对WCNS 格式进行了改进,提出7 阶和9 阶精度的WCNS 格式.并通过数值试验证明了格式的高分辨率和强间断捕捉能力.为了进一步提高WCNS 格式在复杂流体计算中的应用,Deng等[24]构造了混合半节点和节点的加权紧致非线性格式 (HWCNS),使得格式在间断区域有了更高的分辨率.Nonomura 等[25]设计一种更加健壮的混合型WCNS 格式.Wong 等[26]提出局部耗散加权紧致格式 (WCNS-LD).该格式在光滑区域使用耗散较小的中心插值模板,在包含间断区域使用耗散较大的迎风插值模板以抑制非物理振荡.Zhao 等[27]提出一种新的可调参数的光滑度量指标,进一步提高了WCNS 格式的间断捕捉能力和健壮性.洪正等[28]采用5 阶WCNS 格式对各向同性湍流通过正激波的情形进行直接数值模拟.Jiang 等[29]为HJ 方程设计了5 阶精度的WCNS 格式,该格式相比于同阶WENO 格式具有更好的收敛性和分辨率.Hiejima[30]基于TENO 插值思想,建立WCNS-T 格式.相比传统的WCNS 格式,WCNS-T 格式在强不连续和高频间断的捕捉上更具优势.Jiang 等[31]针对等熵Navier-Stokes 方程组提出半隐式时间推进的WCNS格式,避免显式WCNS 格式严格的CFL 稳定性限制.Ma 等[32]构造了非线性紧致插值的WCNS 格式,数值验证新的WCNS 格式可用于大涡模拟.

本文在Jiang 等[29]提出的5 阶精度WCNS格式基础上,进一步构造了非稳态HJ 方程的7 阶精度WCNS 格式.HJ 方程的Hamilton 数值通量采用具有单调性的Lax-Friedrichs 方法计算,一阶空间导数的左、右极限值采用高阶精度混合节点和半节点型的8 阶中心差分格式计算,半节点函数值采用7 阶WENO 型非线性插值方法计算.3 阶TVD Runge-Kutta 方法[33]用于HJ 方程的时间离散.最后通过一系列一维和二维数值算例验证WCNS 格式在精度,分辨率和间断捕捉能力等方面的特性.

1 数值方法

1.1 一维HJ 方程的WCNS 格式

考虑如下形式的一维非稳态HJ 方程

为简单起见,采用均匀网格,即网格节点设置为xi=a+i∆x(i=0,1,···,N).其 中,∆x=(b−a)/N为 网格尺寸,N为网格数.方程(2)的半离散格式为

对式(10)右端在半节点xi+1/2处进行Taylor 展开,得到

其中,B k(k=0,1,2,3) 为与 ∆x无关的常系数.半节点函数值 ϕi+1/2的高阶线性逼近式(7)可由式(10)中4 个低阶线性逼近的线性组合得到

其中,d0=1/64,d1=21/64,d2=35/64,d3=7/64 为理想线性权重.

当所有子模板都处于光滑区域时,非线性权重等于线性权重,得到7 阶精度的半节点函数逼近;当某些子模板包含间断区域时,令其非线性权重趋于零,防止插值穿过间断区域,最后得到4 阶精度的半节点函数逼近.本文选择WENO-Z 型非线性权重,定义如下

式中,k=0,1,2,3 ,参数 ε 取值为小量1 0−20,以避免分母为0.为了使得所设计WCNS 格式在光滑区域能达到7 阶精度,全局光滑度量指标 τ 定义为τ =|IS3−IS2−IS1+IS0|.其中,ISk是子模板Sk(k=0,1,2,3)的光滑度量指标,定义如下

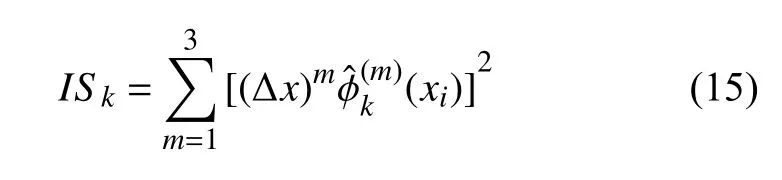
对于半离散格式(3),采用如下3 阶显式TVD Runge-Kutta 方法[33]求解

1.2 二维HJ 方程的WCNS 格式

考虑如下形式的二维非稳态HJ 方程

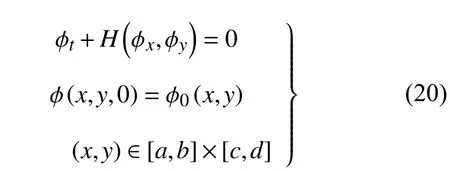
这里同样考虑均匀网格,即网格节点设置为xi=i∆x(i=0,1,···,M),yj=j∆y(j=0,1,···,N).其中,x和y方向的网格尺寸分别为 ∆x=(b−a)/M,∆y=(d−c)/N,网格数为M×N.

方程(20)的半离散格式为

2 WCNS 格式的精度分析

基于一维HJ 方程,式(13)改写为如下形式

将其代入式(5)得到

因此,WCNS 格式达到最佳7 阶精度的充分条件为

3 数值实验

本节数值测试7 阶WCNS 格式的性能.在精度测试算例中,∆t=(∆x)7/3,L1和L∞范数数值误差定义如下

其中,ϕe表示精确解或细网格上得到的参考解.本文所有数值实验均在Visual Studio 2017+Intel Visual Fortran 的软件平台和CPU Xecon E3-1230+内存12 GB 的台式电脑上完成.

3.1 精度测试

考虑一维线性HJ 方程

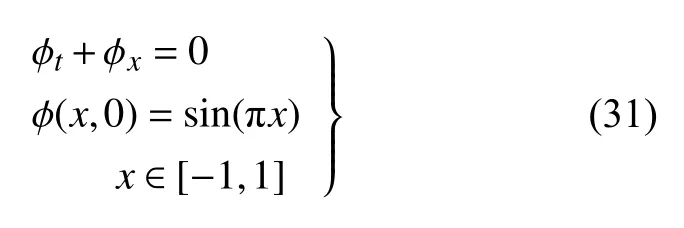
以及二维线性HJ 方程

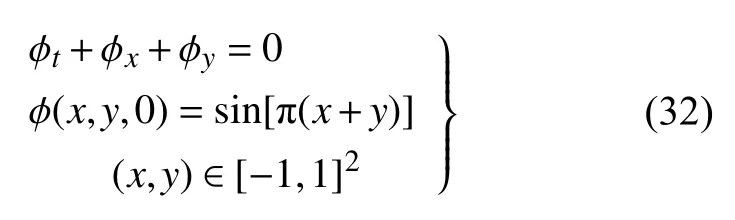
以上方程均考虑周期边界条件,并分别计算至t=5 和t=0.5.表1 和表2 分别给出了一维和二维情形下由WCNS 格式和WENO 格式所得的L1和L∞数值误差、精度阶和CPU 运行时间.由表可知,相比WENO 格式,WCNS 格式在光滑区域能达到所设计的7 阶精度,其在精度和收敛性上明显优于经典的WENO 格式.图1 给出了两种格式的L∞数值误差与CPU 时间关系曲线图.由此可知,当获得相同L∞数值误差时,WCNS 格式所耗的CPU 时间比WENO 格式少,因此计算效率略高.

表1 一维情形时两种格式的数值误差、精度阶和CPU 运行时间Table 1 Numerical errors,convergence rates and CPU time obtained with two schemes for the 1D case

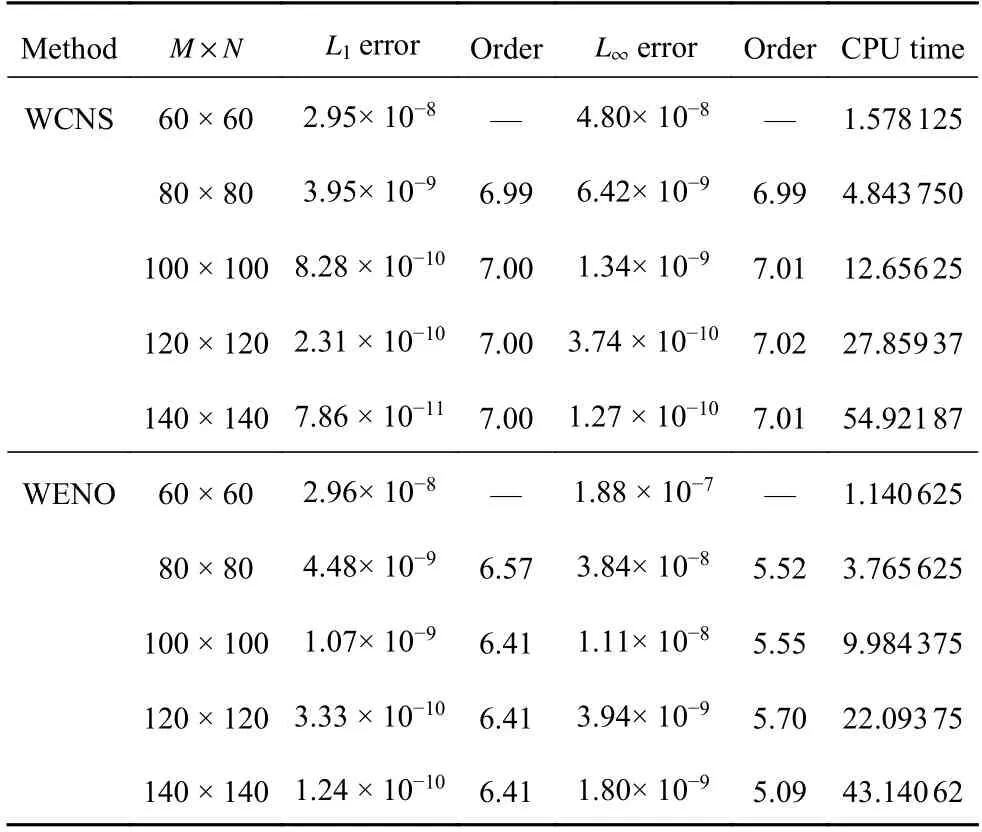
表2 二维情形时两种格式的数值误差、精度阶和CPU 运行时间Table 2 Numerical errors,convergence rates and CPU time obtained with two schemes for the 2D case

图1 两种格式的计算误差与CPU 时间关系曲线图Fig.1 CPU times against numerical computing errors obtained with two schemes

3.2 分辨率测试

考虑满足周期边界条件的一维HJ 方程: ϕt+ϕx=0,x∈[−1,1].本例测试两种初值条件下格式的分辨率.第1 种初值条件为

网格数设置为N=100.采用7 阶WCNS 格式和7 阶WENO 格式计算本例.图2 给出了基于初值条件(33)在t=11 时刻的数值结果,图3 分别给出了基于初值条件(34) 在t=2 时刻和t=8 时刻的数值结果.由图可知,WCNS 格式相比WENO 格式在间断点附近具有更高的分辨率.在后面算例中仅采用7 阶WCNS 格式计算.

图2 基于初值条件(33)在 t=11 时刻所得数值解比较Fig.2 Comparisons of numerical solutions at time t=11 based on the initial condition (33)

图3 基于初值条件(34)在不同时刻所得数值解比较Fig.3 Comparisons of numerical solutions at different times based on the initial condition (34)

3.3 一维凸和非凸Hamilton 问题[11]

考虑一维具有凸Hamilton 函数的HJ 方程

以及一维具有非凸Hamilton 函数的HJ 方程

考虑周期边界条件,并采用三种粗细不同的网格,即网格数设置为N=50,100,200.采用7阶WCNS格式对以上两个方程分别计算至此时两个方程的解均会出现间断.图4 给出了基于两个方程在不同网格下所得数值解.由图可知,在3 种网格下所得数值解与参考解均吻合得很好.此外,WCNS 格式具有很好的间断捕捉能力.

图4 一维(a)凸和(b)非凸Hamilton 问题的数值解Fig.4 Numerical solutions of 1D (a) convex and (b) nonconvex Hamilton problems

3.4 二维凸和非凸Hamilton 问题

考虑二维具有凸Hamilton 函数的HJ 方程

和二维具有非凸Hamilton 函数的HJ 方程

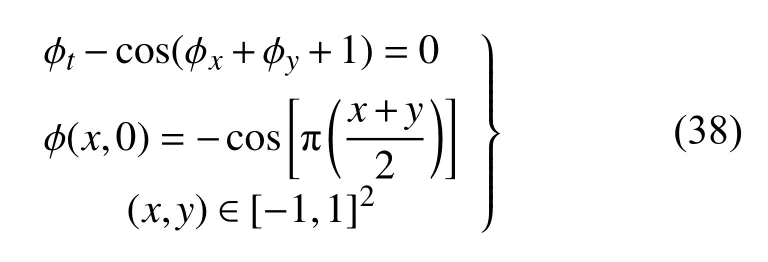
考虑周期边界条件,并采用3 种粗细不同的网格,即网格数为M×N=50×50,100×100,200×200.两个方程分别计算至以测试WCNS 格式对间断解的捕捉能力.图5 和图6 分别给出了基于两个方程在50×50 网格下所得数值解的曲面图和在各种网格下沿直线x=y的截面图.由图可知,WCNS格式对于该算例也具有很好的间断捕捉能力.此外,在3 种网格下所得数值解与参考解均吻合得很好,因此,在后面算例中均考虑粗网格,即网格数为 5 0×50.

图5 二维凸Hamilton 问题的数值解(a)曲面图和(b)截面图Fig.5 (a) Surface and (b) cross-sectional diagram of the numerical solution of the 2D convex Hamilton problem

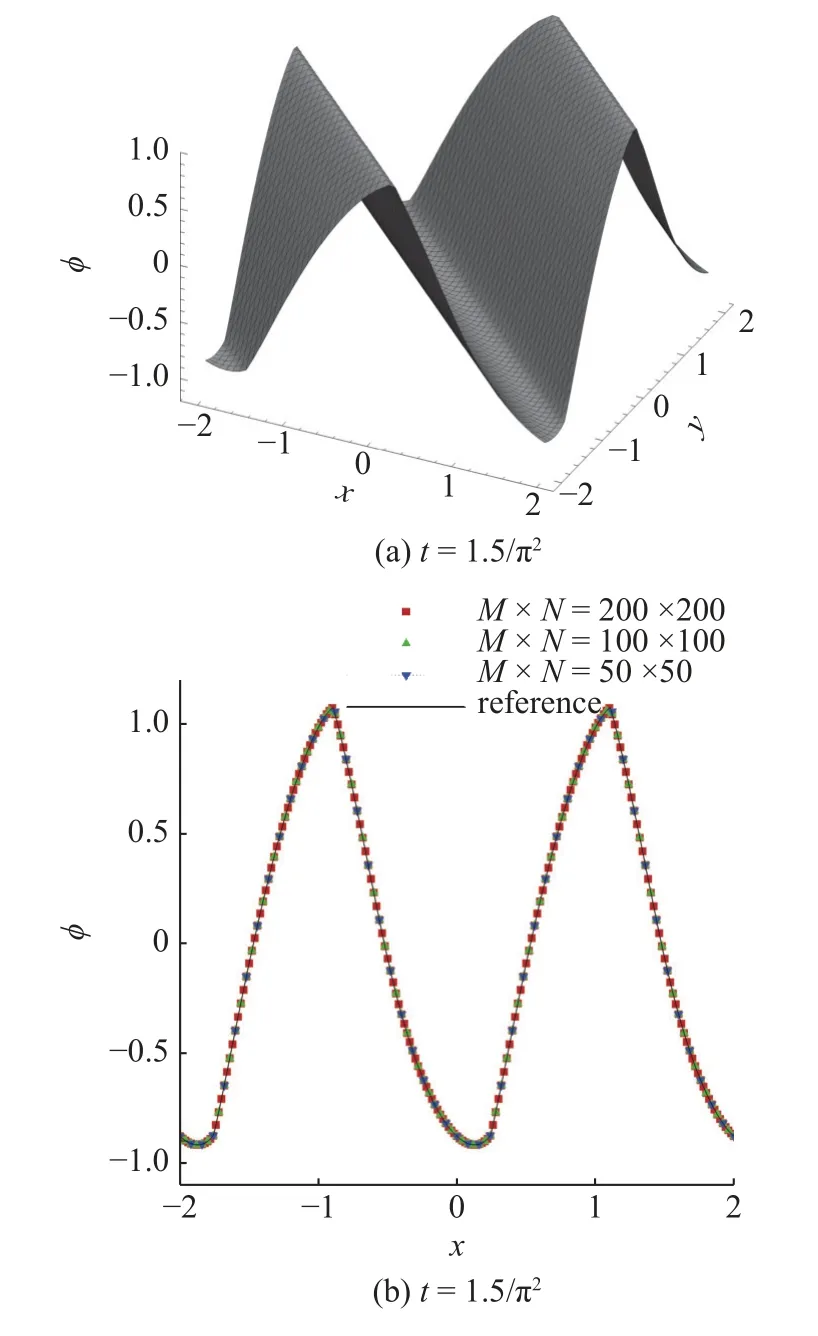
图6 二维非凸Hamilton 问题的数值解(a)曲面图和(b)截面图Fig.6 (a) Surface and (b) cross-sectional diagram of the numerical solution of the 2D nonconvex Hamilton problem

3.5 二维完全问题[10]

求解周期边界条件下二维HJ 方程

该问题具有精确解

其中,x=q−tsinr,y=r+tcosq.当t<1.0 时,方程具有光滑解;当t≥1.0 时,方程的解会出现间断.图7给出了t=0.8 时刻和t=1.5 时刻数值解的曲面图和沿直线x=y的截面图.由图可知,数值解和精确解吻合,在间断附近WCNS 格式基本无振荡.

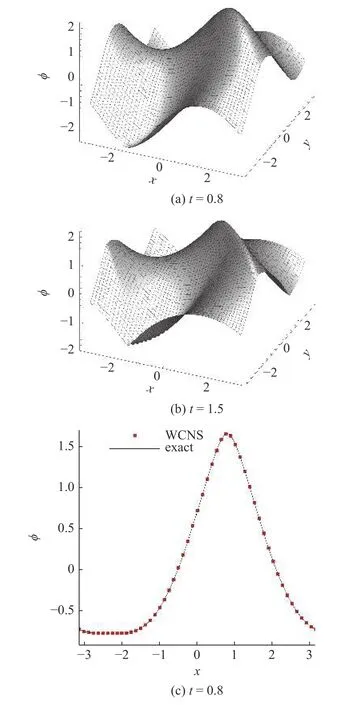
图7 二维完全问题的数值解(a),(b) 曲面图和(c),(d)截面图Fig.7 (a),(b) Surfaces and (c),(d) cross-sectional diagrams of numerical solutions of the fully problem

3.6 二维最优控制问题 [13,15]

图8 二维最优控制问题的数值解(a),(b)曲面图和(c),(d)截面图Fig.8 (a),(b) Surfaces and (c),(d) cross-sectional diagrams of the numerical solutions of the optimal control problem

图8 二维最优控制问题的数值解(a),(b)曲面图和(c),(d)截面图 (续)Fig.8 (a),(b)Surfaces and (c),(d) cross-sectional diagrams of the numerical solutions of the optimal control problem (continued)

求解周期边界条件下二维最优控制问题的截面图.由图可知,WCNS 格式精度高、分辨率好.

3.7 二维传播面问题[19,29]

求解周期边界条件下二维传播面问题

图9 二维传播面问题的 ε=0 时数值解Fig.9 Numerical solutions of the propagating surface problem with ε=0

其中,ε >0 为一个很小的常数,K为平均曲率了 ε=0 和 ε=0.1 时不同时刻下的数值解曲面图.由图可知,WCNS 格式在数值模拟该问题时基本无振荡,具有很好的分辨率.

图10 二维传播面问题的 ε=0.1 时数值解Fig.10 Numerical solutions of the propagating surface problem with ε=0.1

4 结论

本文针对非稳态HJ 方程设计了7 阶精度WCNS 格式.采用单调的Lax-Friedrichs 型通量分裂方法计算Hamilton 数值通量,8 阶精度的混合型中心差分格式近似节点处一阶空间导数的左、右极限值,并通过基于七点模板的WENO 型非线性插值方法得到半节点函数值的高阶逼近.3 阶显式TVD Runge-Kutta 时间离散方法用于求解空间离散化后的半离散格式.精度测试算例结果表明,本文提出的WCNS 格式能够很好的模拟HJ 方程的精确解并且在光滑区域能够达到设计的7 阶精度.相比经典的7 阶WENO 格式,WCNS 格式在精度和收敛性方面更优,且获得相同误差时,所耗CPU 时间更短,因此计算效率略高.分辨率测试算例结果表明,相比经典的7 阶WENO 格式,WCNS 格式具有更好的分辨率和更强的间断捕捉能力.其他一维和二维测试算例结果均表明WCNS 格式精度高、分辨率高、间断捕捉能力强.下一步工作,进一步优化全局模板和子模板的光滑度量指标,提高WCNS 格式计算效率.