曲壁蜂窝夹层悬臂板的振动特性研究1)
2022-12-18张君华权铁汉
薛 潇 张君华, 孙 莹 权铁汉
* (北京信息科技大学机电工程学院,北京 100192)
† (北京信息科技大学理学院,北京 100192)
引言
蜂窝是一种有序棱柱状胞元组成的多孔材料,具有制造所需耗材少、结构稳定性好的优势.通过对蜂窝胞元进行设计,蜂窝可以实现负泊松比[1]、负刚度[2]等力学性能,并且可以实现隔热[3]、隔声[4]和隔振[5]等功能.蜂窝夹层板的力学特性很大程度上取决于蜂窝胞元的形状和相对密度,国内外学者对于蜂窝夹层板芯层的研究成果已经非常丰富.Gbison 等[6]对正六边形蜂窝夹层板进行系统的研究,提出了计算蜂窝结构芯层弹性模量的经典等效理论.富明慧等[7]系统地对蜂窝芯等效参数进行了综述.杨稳等[8]从理论公式推导、均匀化法及有限元法等方面对蜂窝芯层等效参数的研究进行分类论述.乐京霞等[9]给出线弹性范围内蜂窝芯层的箭型负泊松比蜂窝夹层板等效力学参数理论公式,并通过拉伸试验验证了公式的准确性.Liu 等[10]设计并制备一种新型的Y 型芯全复合材料夹层结构,并研究了相对密度对力学性能的影响.Ru 等[11]设计了一种具有混凝土状增强层的蜂窝复合材料,具有比蜂窝更高的峰值载荷和更好的能量吸收能力.Albert 等[12]研究了具有不同相对密度的13 种二维蜂窝芯胞元的力学性能和变形模式.Zwab 等[13]提出一种可定制有效弹性模量的混合分层方形蜂窝,分析了结构参数和相对密度对有效弹性模量的影响.
传统正六边形蜂窝在面内变形的力学行为主要是直壁和斜壁的拉压和弯曲变形,直壁间的节点受力很容易出现应力集中的问题,将直壁换成曲壁后能在一定程度上改善这个问题.Lee 等[14]发现啄木鸟的喙在微观结构上是由波浪形曲线拼接而成的多孔结构,这种弯曲的边界能保护啄木鸟头部.Yang等[15]将正六角形蜂窝等几种蜂窝的直壁替换成波浪形的曲壁,发现替换后的蜂窝具有更好的耐撞性.Deng 等[16]提出一种负泊松比正弦弯曲蜂窝结构,并分析其力学性能.发现正弦弯曲蜂窝在面内冲击下具有较好的耐撞性能.
曲壁蜂窝不仅能缓解直壁的应力集中问题,还有负刚度特性,将蜂窝的直壁替换为正弦屈曲梁的负刚度蜂窝在近年来受到广大学者的关注,这种蜂窝可以经受压缩加载和卸载的多次重复循环,并且具有很高的能量吸收性能和隔振性能.Qiu 等[17]发现了负刚度蜂窝的可重用性,并可以提供可定制的、近乎理想的冲击隔离.Restrepo 等[18]发现通过参数设计,负刚度蜂窝可以达到和正六边形蜂窝相同的比吸收能和平台应力值.Debeau 等[19]通过试验发现负刚度蜂窝可以提供近理想的加速度冲击隔离,并且受冲击后变形可完全恢复.Chen 等[20]设计了一种梯度负刚度GNS 蜂窝结构,通过隔振试验发现GNS 蜂窝比普通负刚度蜂窝具有更好的减振性能.
蜂窝夹层板因其优异的力学特性,通常用于对材料要求苛刻的航空航天领域中.结构的振动是飞行器飞行过程中不可避免的,对振动问题的忽视往往会造成灾难性的后果,因此研究蜂窝结构的非线性振动问题具有重要意义.Di 等[21]研究了蜂窝单元的不同几何参数对负泊松比夹层板自由振动响应的影响.Li 等[22]比较了泡沫铝夹芯圆柱壳、传统蜂窝夹芯圆柱壳和负泊松比六角形蜂窝夹芯圆柱壳在爆炸荷载作用下的动力学响应.Wu 等[23]对铝蜂窝夹层板在冰楔冲击下的动态响应和能量吸收特性进行了数值和实验研究.Ma 等[24]在随机振动载荷下对复合蜂窝夹芯板进行了疲劳试验,并提出一种预测复合蜂窝夹层结构在随机振动载荷下的疲劳寿命的方法.Zhang 等[25]建立了旋转整体叶盘的非线性运动控制方程.研究了调谐和失谐整体叶盘的自由振动和模态局部化现象.陈永清等[26]运用Hoff 理论对类蜂窝夹层结构进行振动特性分析,计算类蜂窝夹层结构在四边简支边界条件下的振动固有频率方程解.对于蜂窝夹层板振动特性的研究,大多都集中于理论推导并运用有限元方法进行验证.进行振动试验的较少.Arunkumar 等[27]对蜂窝夹层结构自由振动和受迫振动进行了数值和实验研究,数值得到的结果与实验结果吻合良好.闫昭臣等[28]利用振动台测定了具有3 种泊松比的蜂窝夹层板的固有频率,并对夹层板进行了冲击试验.何贵勤等[29]对挠性航天器太阳翼进行了振动试验,经试验测定的振动特性与理论模型相一致,杨雨恒等[30]利用锤击法测定了自由边界的铝制蜂窝夹层板的固有频率.
本文基于以上的研究,采取力学等效方法推导曲壁蜂窝芯的等效力学参数,建立曲壁蜂窝夹层板的动力学模型,计算得出板的固有频率,并应用有限元软件对动力学模型进行验证.通过3D 打印曲壁蜂窝夹层板,对蜂窝夹层板进行脉冲激励试验,定频驻波试验和冲击试验,试验结果验证理论模型,并研究了曲壁蜂窝的抗冲击性能.
1 曲壁蜂窝夹层板动力学模型建立及求解
本文提出一种新型曲壁蜂窝芯夹层板,夹层板结构如图1 所示,蜂窝芯胞元由可变弧长、弧度的圆弧和支撑圆弧的直壁组成.

图1 曲壁蜂窝夹层板Fig.1 Curved-wall honeycomb sandwich plate
1.1 曲壁蜂窝芯的等效弹性参数计算
本节推导曲壁蜂窝胞元的面内等效弹性参数,曲壁蜂窝胞元形状如图2 所示,θ 为圆弧所对应弧度,R为圆弧半径,b为单胞厚度,单胞直壁长度为 2h,单胞在x方向长度为L x,单胞在y方向长度为 2Ly.
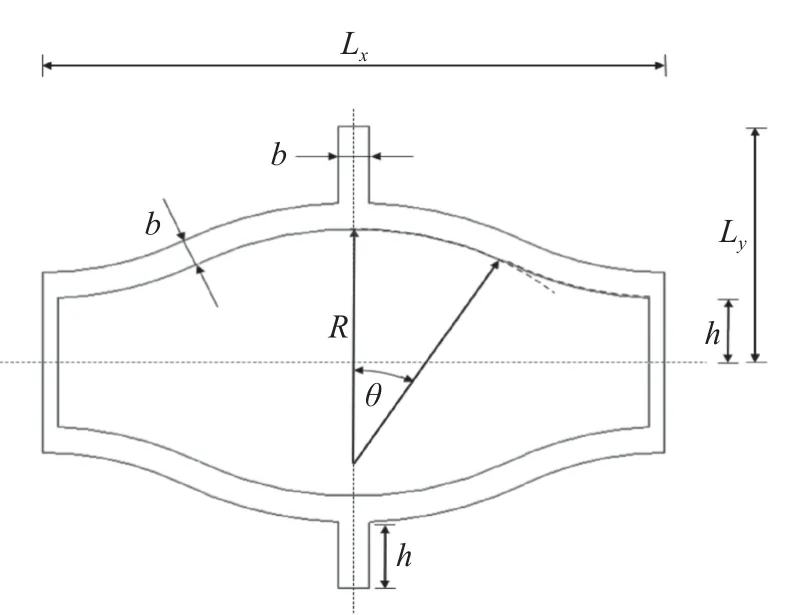
图2 曲壁蜂窝单胞Fig.2 Cell of curved-wall honeycomb
从单胞中选取曲梁为研究对象如图3 所示,曲梁材料杨氏模量为Es,梁截面惯性矩为I,可计算得不受外力时单胞在x方向的长度为

图3 曲壁蜂窝的曲梁Fig.3 Curved beam of curved-wall honeycomb

在y方向的长度为

弯矩是导致曲梁变形的主要因素,正应力和切应力导致的曲梁变形在本文中忽略不计.当曲梁受到y方向加载时,曲梁的受力情况如图4(a)所示.假设曲梁B点受到 由直梁 作用的y方向的 力F,则A和D两点受到大小为F/2 的剪力,受力后A,B,D点转角为0,弧BD受力关于中点C对称,故C点所受弯矩为0.A和D所受弯矩
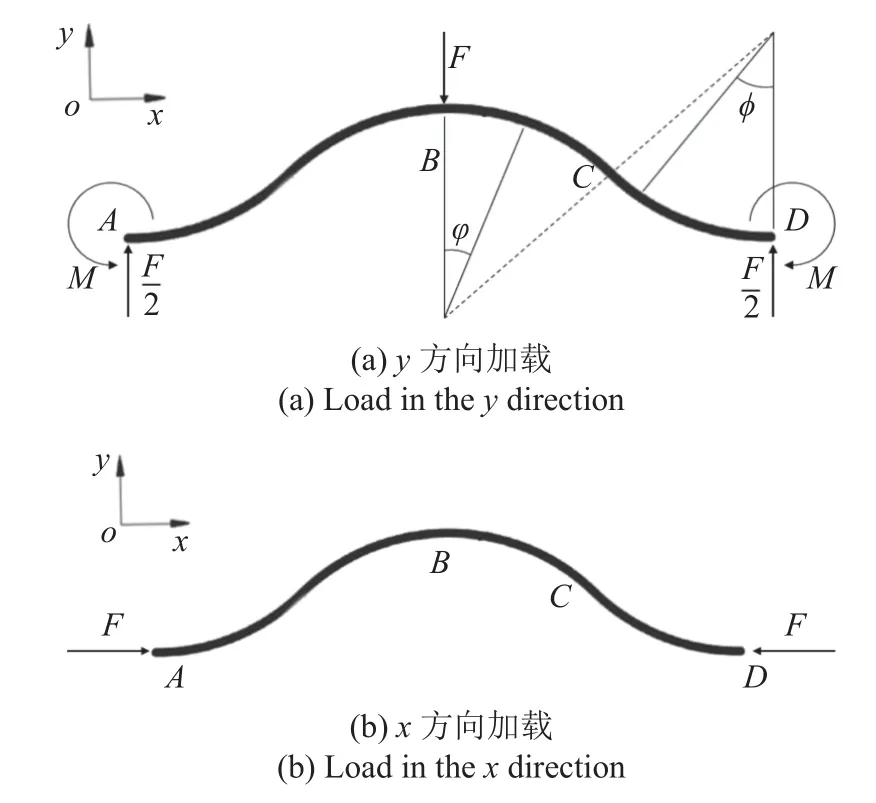
图4 蜂窝曲梁受力分析Fig.4 Force analysis of honeycomb curved beam
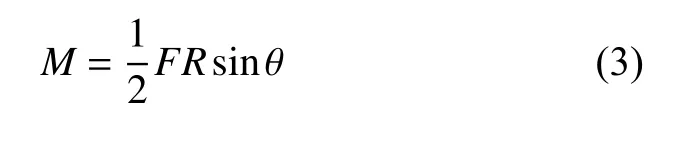
选取弧B CD为研究对象,弧B C和弧C D上的弯矩是关于弧度 φ 和ϕ 的函数M BCy(φ) 和MCDy(ϕ)

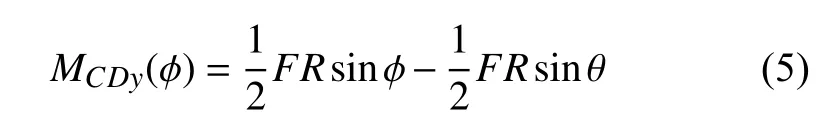
利用单位载荷法计算在y方向加载时Ly的位移变化 ∆yy和L x的位移变化 ∆yx
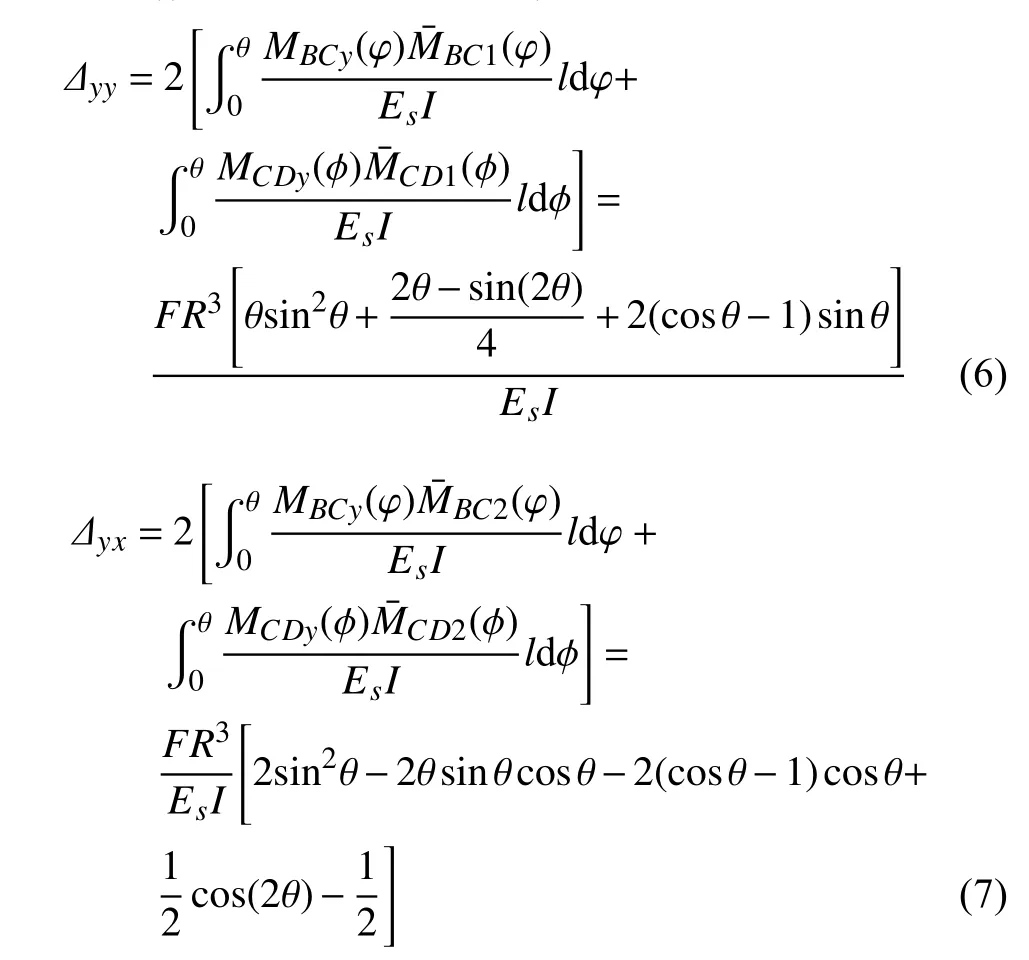
当曲梁受x方向的载荷时,受力情况如图4(b)所示.可求出曲梁在x方向加载时Ly的位移变化 ∆xy和L x的位移变化 ∆xx

曲壁蜂窝芯在y方向上的应力和应变分别为
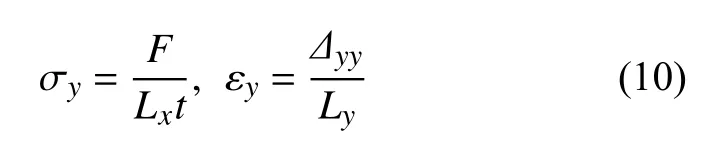
蜂窝芯在z方向上的深度为t,可计算出蜂窝芯在y方向上的等效弹性模量
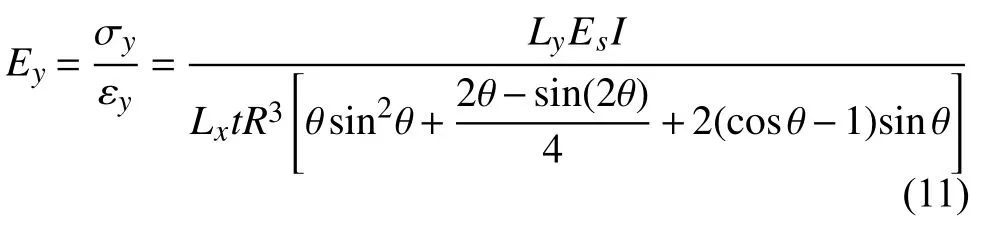
同理可求出蜂窝芯在x方向上的等效弹性模量
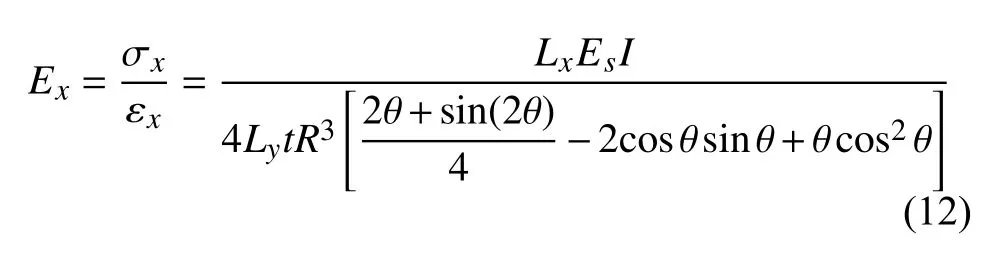
曲壁蜂窝芯在y方向和x方向上的等效泊松比分别为

曲梁在y方向加载后,最大剪切应力发生在曲梁中心点B,剪应力大小可表示为

剪应变用y方向位 移∆yy和z方向的深度t表示为

可得到y方向的剪切模量
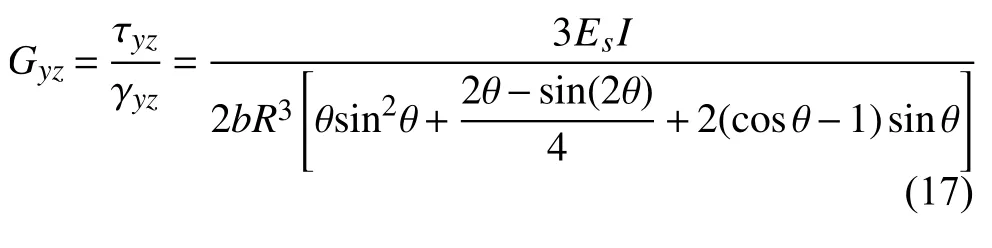
曲壁蜂窝芯作为轻质多孔材料,相对密度是多孔材料的一项重要参数,其相对密度表示为

1.2 悬臂曲壁蜂窝夹层板的模型及固有频率求解
蜂窝夹层板这类轻质材料结构通常用于航空航天等领域,工作环境经常为悬臂边界,故本文选择悬臂边界下的曲壁蜂窝夹层板,研究其振动特性,悬臂边界条件下曲壁蜂窝夹层矩形板的模型如图5 所示,固定端为夹层板的ob边,其余三边均为自由边界.在曲壁蜂窝夹层板的中面内建立平面直角坐标系xOy,z轴通过坐标原点垂直于中面竖直向上.曲壁蜂窝夹层矩形板x方向长度为a,y方向长度为b.曲壁蜂窝夹层板由上下两层厚度为hf的蒙皮和厚度为hc的芯层组成,板受到z方向的均布载荷p0,假设上下蒙皮和芯层紧密黏结.
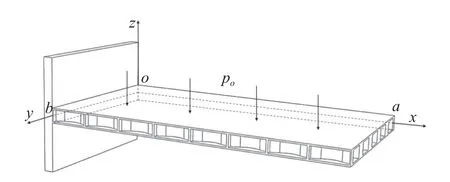
图5 悬臂边界条件下曲壁蜂窝夹层板Fig.5 Cantilever curved-wall honeycomb sandwich plate
选取曲壁蜂窝夹层板的基体材料为聚乳酸(PLA),其弹性模量为Es,密度为 ρs,泊松比为 νs,剪切模量为Gs.曲壁蜂窝夹层板发生自由振动时动能可以表示为
势能表示为
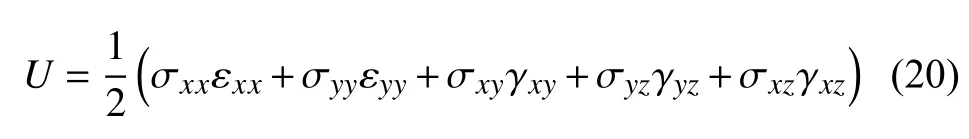
其中u,ν,w分别为板材中面(即z=0)上任意一点沿x,y,z方向上的位移,ϕx和 ϕy分别为曲壁夹层板中面的法线相对于x轴和y轴的转角.根据经典板理论,位移场中各函数的表达式为
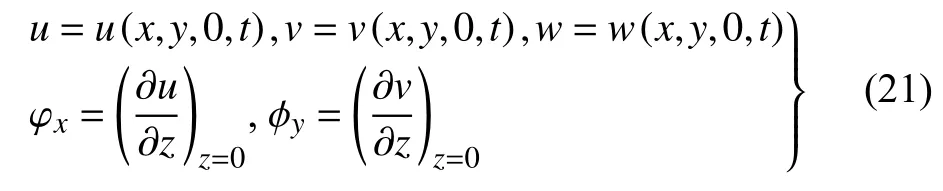
曲壁蜂窝夹层板的应变分量可表示为[31]
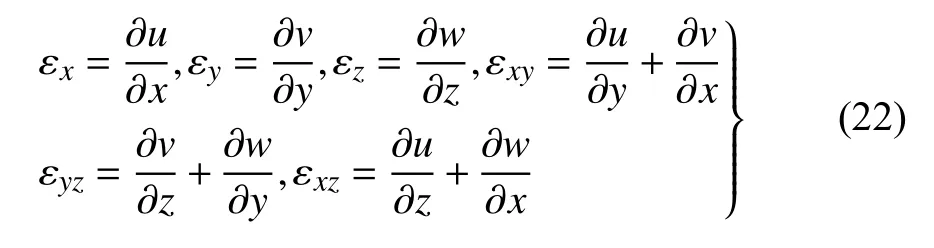
曲壁蜂窝夹层板为各向异性,其本构方程可表示为如下形式[31]

式中,上角标k=1,3 表示曲壁蜂窝夹层板的上下蒙皮,k=2 表示曲壁蜂窝夹层板的曲壁蜂窝芯,刚度系数具体表达形式为

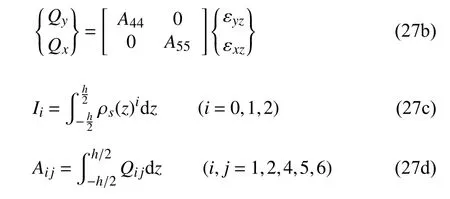
利用Chebyshev-Ritz 法求解悬臂板的固有频率,假设夹层板的横向振动位移和转角位移函数表达式为[32]
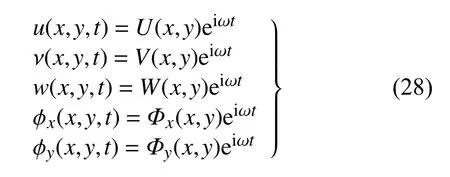
式中,U(x,y),V(x,y),W(x,y),Φx(x,y),Φy(x,y) 均表示振型函数,这些振型函数可以用Chebyshev 函数展开为

式中,U mn,Vmn,Wmn,Φxmn,Φymn为待定系数,其中
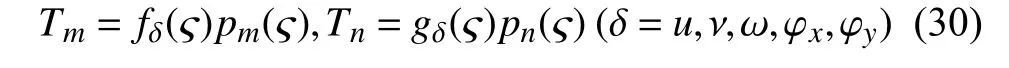
l阶的第一类Chebyshev 多项式可写为
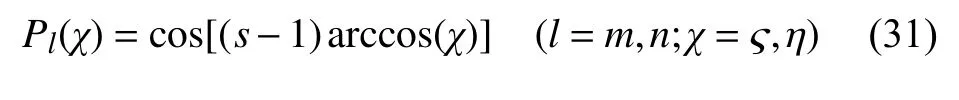
将式(28)~式(31)代入动能和势能表达式(25)和式(26)中,在积分域中积分,可得到曲壁蜂窝夹层板的最大动能Tmax和最大势能Umax.函数 Π=Umax−Tmax,令

式(32)可转为以下矩阵形式
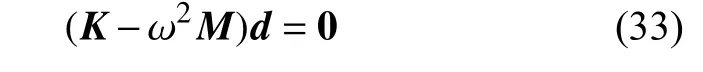
式中,ω 为固有频率,K和M分别表示刚度矩阵和质量矩阵.d表示特征向量,可写为

Chebyshev 法是一种截断法,为了权衡收敛性和运算效率,利用该方法求解曲壁蜂窝夹层板的固有频率时需要找到一个合适的截断阶数.通过计算不同截断阶数下系统的第一阶固有频率,发现在截断阶数为7 时,曲壁蜂窝夹层板第一阶固有频率基本收敛 (图6).
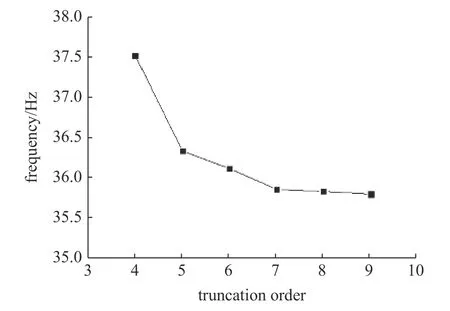
图6 不同截断数下夹层板的第一阶固有频率Fig.6 The first natural frequency of the sandwich plate with different truncation orders
2 曲壁蜂窝夹层结构振动试验
搭建如图7 所示的悬臂板振动试验平台.测量曲壁蜂窝夹层板各点在扫频过程的激励随频率的变化,计算出频响曲线,并与理论模型和有限元模型得到的结果做对比.

图7 振动试验平台Fig.7 Vibration test platform
采用极光尔沃公司的A8S 型3D 打印机打印试验用的曲壁蜂窝夹层板,材料选取聚乳酸PLA.3D 打印机精度的限制导致打印误差,制备试件的微观组织存在材料不均匀的问题,因此打印后材料的力学特性与基材存在一定差异.针对这一问题,利用3D 打印机制作了拉伸试样,并利用万能试验机进行拉伸试验,万能试验机和拉伸试件如图8 所示.试验获得了材料应力−应变曲线如图9 所示,经计算得到3D 打印后材料的杨氏模量约为1660 MPa,PLA的泊松比为0.2[31],密度为12.5 g/mm3.制备的试件曲壁半径R=20 mm,直壁高h=5 mm,曲壁弧度θ=π/6,蒙皮厚度hf=1.5 mm,芯层厚度hc=12 mm,单胞在x轴方向长度Lx=40 mm 在y轴方向长度Ly=17.36 mm,壁厚b=2 mm,制备的夹层板长320 mm,宽173.58 mm,厚15 mm.

图8 准静态拉伸试验及试样Fig.8 Quasi-static tensile test and test specimens
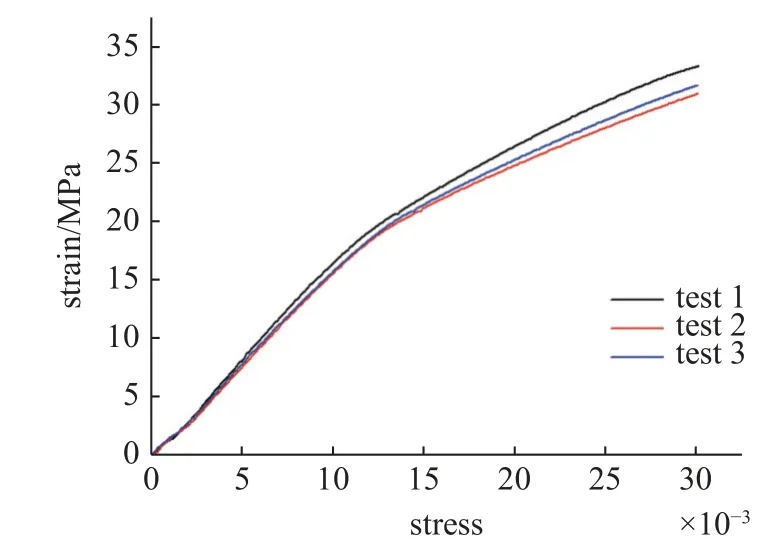
图9 试验测得的试样的应力−应变曲线Fig.9 Stress-strain curves from test
搭建的振动测试平台主要由杭州亿恒振动控制公司的MP102 型功率放大器、INV3062 T 型信号采集仪和航天希尔公司的L620 M 型振动台组成,加速度传感器采用奇石乐公司的INV-9828 型加速度传感器.试验工况如图10 所示,应用夹具和螺栓螺母将蜂窝夹层板固定到振动台上.在曲壁蜂窝夹层板的激励端、中间端、自由端、角端和侧端放置加速度传感器,分别测量曲壁蜂窝夹层板面外和面内横向方向的响应.

图10 振动试验工况及测点位置Fig.10 Vibration test condition and position of test points
为了测量曲壁蜂窝芯的隔振性能,利用3D 打印机制备如下曲壁蜂窝结构试件: 曲壁半径R=40 mm,直壁高h=5 mm,曲壁弧度 θ=π/6,芯层厚度hc=12 mm,壁厚b=2 mm 的曲壁蜂窝芯,隔振试验工况如图11 所示,在激励端和曲壁蜂窝芯顶端放置了加速度传感器以测量冲击激励信号和响应信号.

图11 蜂窝芯振动试验工况及测点位置Fig.11 Conditions of honeycomb core vibration test and position of test points
3 有限元模型的建立
为了模拟曲壁蜂窝结构在振动台上的动力学响应,使用有限元法求解器ABAQUS 进行了模拟.在有限元模型中,选取的网格为1 0 节点六面体C3D10 单元,建立了如图12 所示的有限元模型,在有限元软件划分网格过程中考虑的网格收敛性问题,经过多网格尺寸模型的仿真结果,发现当网格尺寸大小为0.5 mm 时夹层板的第一阶固有频率已经收敛,如图13 所示.故本文中有限元模型的网格尺寸选择为0.5 mm.设定PLA 材料的力学参数,包括杨氏模量E=1660 MPa、泊松比v=0.2,模拟加速度为0.2g的振动台扫频过程,见图3.
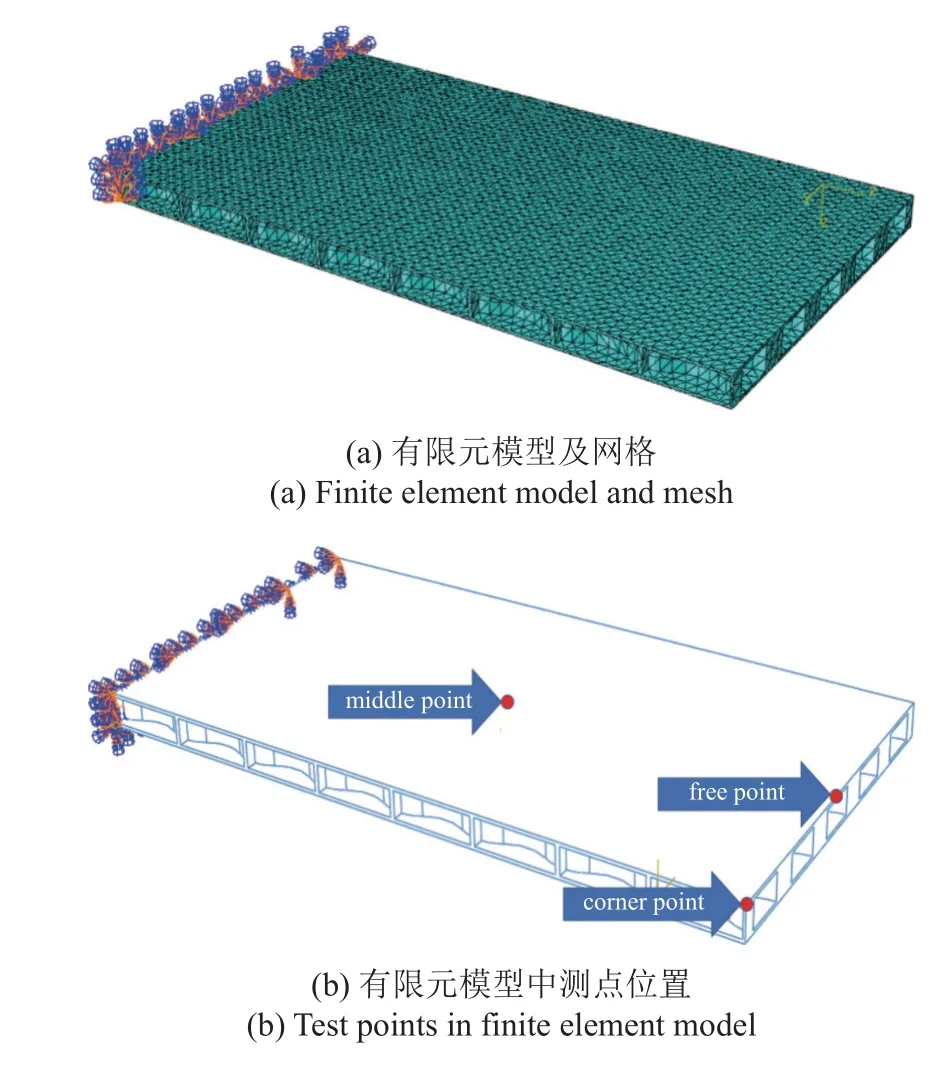
图12 曲壁蜂窝夹层板有限元模型Fig.12 Finite element model of honeycomb sandwich plate with curved wall
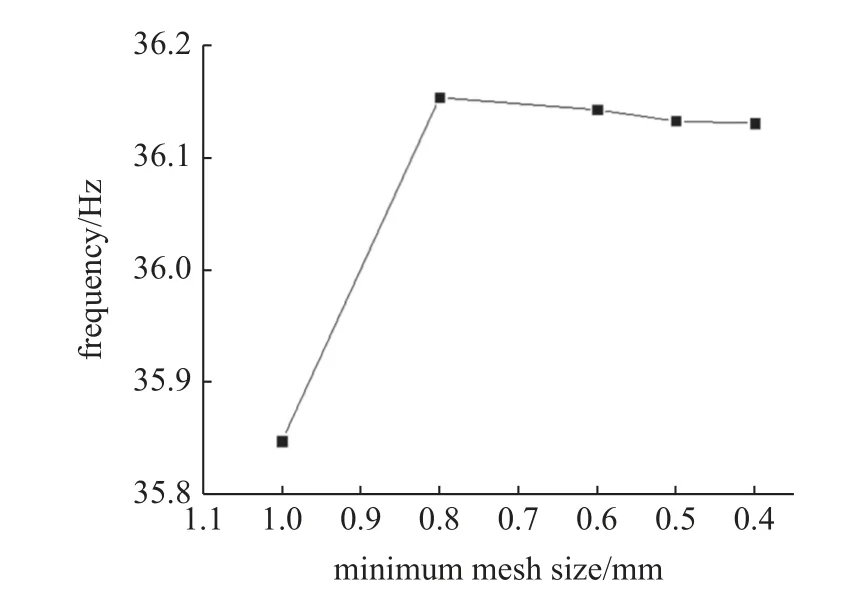
图13 有限元模型网格收敛性分析Fig.13 Analysis of mesh convergence of finite element model
4 结果与讨论
4.1 曲壁蜂窝夹层板扫频试验与仿真结果
通过信号采集仪获得的激励端、中端、自由端和角端的扫频频响曲线如图14 所示.试验发现安装在侧端的传感器没有响应,原因可能为夹层板面内振动幅度较小,传感器量程不足导致漏测.

图14 0~1000 Hz 扫频过程中测点响应Fig.14 Response of test point during 0~1000 Hz
从频响曲线中可获得可能的曲壁蜂窝夹层板前几阶固有频率,对蜂窝夹层板进行频率为1 阶和3 阶固有频率的定频谐波驻留实验,作用时间10 s,限制位移峰值2 mm.激励频率为31.25 Hz 和254 Hz时,定频激励下曲壁蜂窝夹层板的幅频响应特性如图15 所示.由图15(a)可知,当激励频率为31.25 Hz时,曲壁蜂窝夹层板除了在31.25 Hz 处的主共振外,还激发了多个超谐共振;而当激励频率为254 Hz 时,只有主共振.在激励频率为1 阶固有频率时,曲壁蜂窝夹层板的振动产生的位移较大.

图15 曲壁蜂窝夹层板在定频驻波试验中的响应Fig.15 Responses of honeycomb sandwich plate in constant frequencies standing wave test
对所建立的有限元模型进行模态分析,可得曲壁蜂窝夹层板的前5 阶固有频率及振型.理论模型、有限元模型和试验得到的前5 阶固有频率如图16 所示,表1 为夹层板理论解与有限元模型求解和试验得到的前5 阶固有频率对比.根据有限元模型得出的振型发现悬臂边界下的第4 阶振型模态为板在x方向的往复摆动,由于试验中侧端未测量到有效的响应,故无法从试验中得出曲壁蜂窝夹层板的第4 阶固有频率.从数值上可以发现理论模型与有限元模型求到的前5 阶固有频率最大误差为4.93%,最小误差为0.57%,理论模型与试验所得结果的误差也在可以接受的范围内,这些在一定程度上都可以说明理论模型的正确性.

表1 前5 阶固有频率结果对比Table 1 Comparison of the first 5 order natural frequencies results
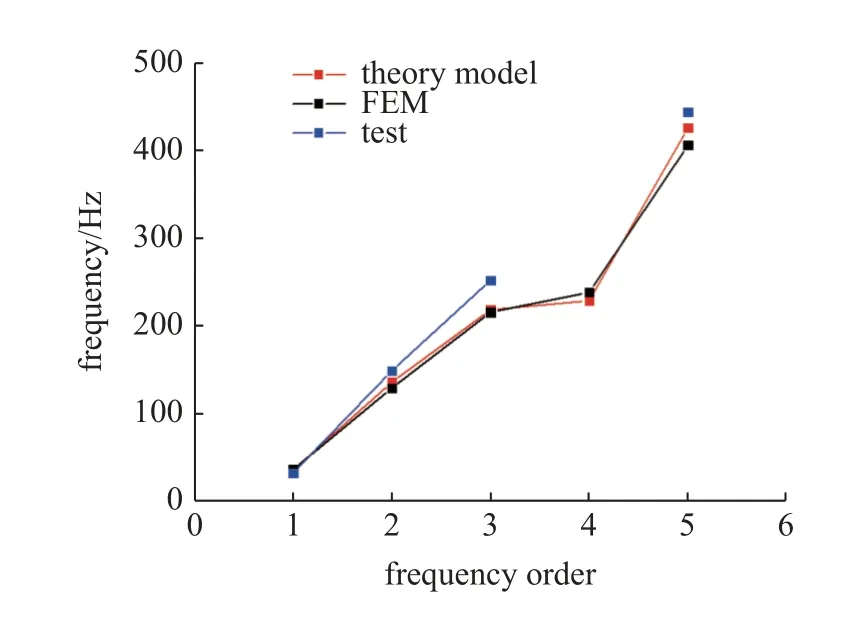
图16 曲壁蜂窝夹层板的前5 阶固有频率Fig.16 The first 5 order natural frequencies of curved-wall honeycomb sandwich plate
图17 为试验和有限元模型的扫频频响曲线对比,可以发现两者规律大体一致,曲线走势大致相同.这说明在相同频率激励下,试验与有限元模型的响应相同,即同阶固有频率下的振型相同.理论模型和有限元模型计算出的曲壁蜂窝夹层板的前3 阶振型如图18 所示,曲壁蜂窝夹层板的1 阶振型为弯曲模态,2 阶为扭转模态,3 阶为拉弯耦合模态.由1 阶模态可以发现模态最大位移出现在结构的自由端.

图17 试验和有限元模型的扫频频响曲线对比Fig.17 Comparison of sweep frequency curves between test and finite element model

图18 曲壁蜂窝夹层板的前3 阶振型对比Fig.18 Comparison of the first three modes of honeycomb sandwich plate
通过对比理论模型和实验求出的前5 阶固有频率,发现最大误差达15.2%,理论模型与试验结果出现较大误差的原因可能有以下几点: (1) 3D 打印机的最小打印精度为0.02 mm,打印出的曲壁蜂窝夹层板材质不够均匀,无法完全满足设计要求;(2)在试验过程中夹具夹紧曲壁蜂窝夹层板的边缘时,会对夹层板产生预紧力的作用,并且这个产生的预紧力在振动试验中会发生动态的变化;(3)理论模型应用的是试验测得PLA 材料的杨氏模量,只考虑了材料在线弹性阶段的变形,并未考虑结构在响应足够大的时候会产生大变形,同时也未考虑材料的黏弹性和阻尼等对试验结果的影响;(4)未考虑加速度传感器对试验结果的影响,金属传感器使蜂窝夹层板在试验过程中质量分布变得不均匀,并且增大了板的质量.
4.2 曲壁蜂窝夹层板的参数研究
基于已建立的曲壁蜂窝夹层板动力学模型,研究单胞的几何参数对蜂窝夹层板的前5 阶固有频率的影响.选取的材料参数与第3 节中一致.壁厚、曲壁半径和曲壁弧度对前5 阶固有频率的影响分别如表2~表4 所示.从表中的数据可以发现随着蜂窝胞元壁厚的增加,蜂窝夹层板的前5 阶固有频率整体呈现减小趋势.随着单胞曲壁半径的增大,蜂窝夹层板的固有频率逐渐增大.当曲壁弧度在30°~75°的范围内,夹层板的固有频率随着曲壁弧度的增大而增大.
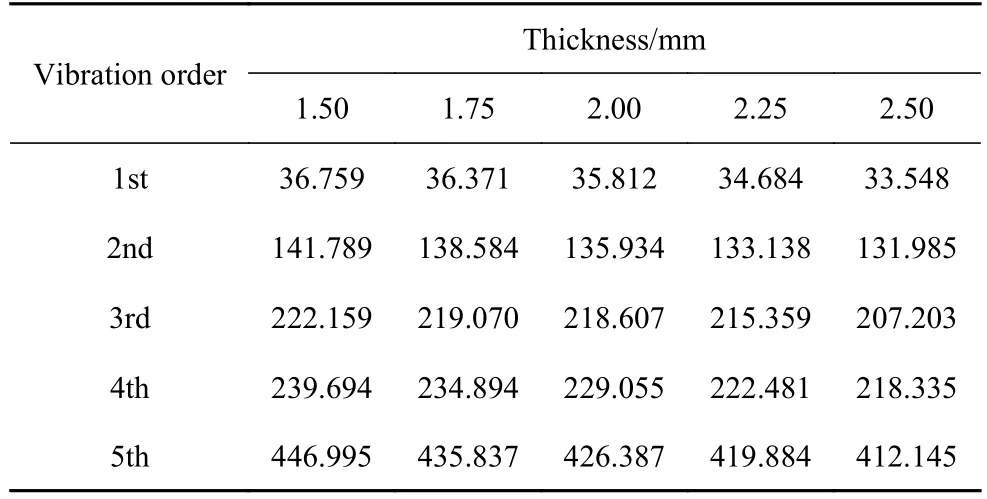
表2 不同壁厚夹层板的固有频率Table 2 Natural frequencies of sandwich plate with different wall thicknesses
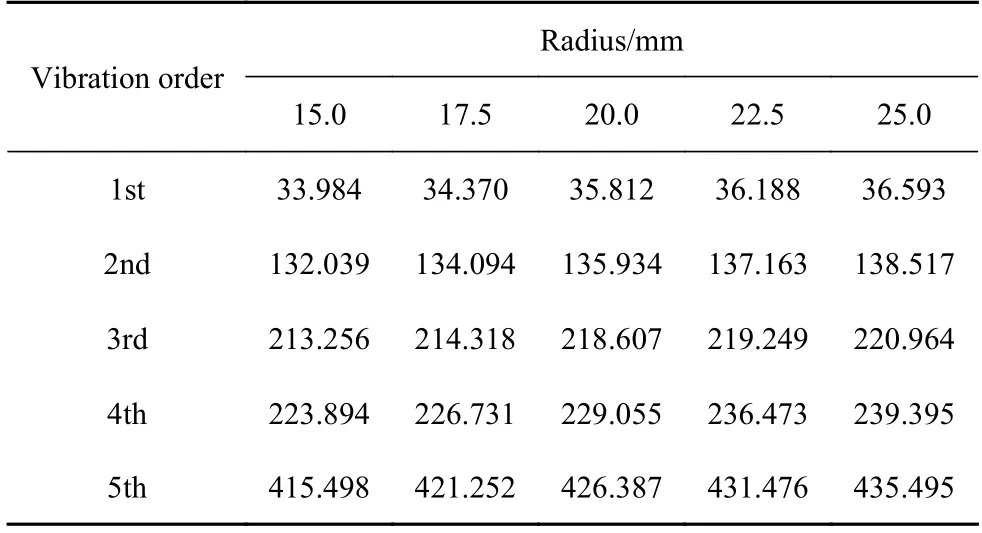
表3 不同曲壁半径夹层板的固有频率Table 3 Natural frequencies of sandwich plate with different curved radius
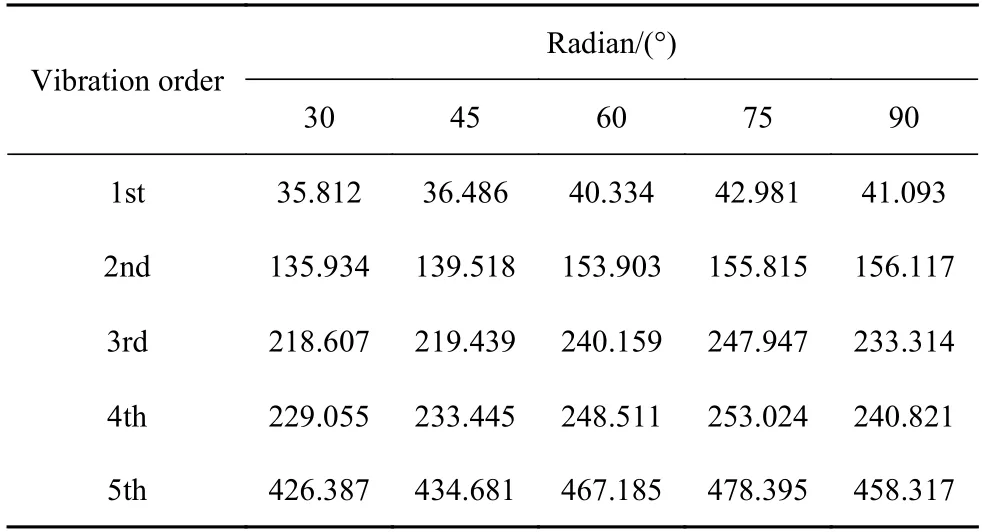
表4 不同曲壁弧度夹层板的固有频率Table 4 Natural frequencies of sandwich plate with different curvature radian
4.3 曲壁蜂窝芯的隔振与抗冲击试验
本节隔振试验测试曲壁蜂窝芯的响应加速度以表征结构的隔振性能.振动台设置的激励范围为15~1000 Hz.振动加速度为0.1 m/s2.定义加速度传递率为输出加速度与输入加速度的比值,作为频率的函数,可表示为

图19 显示了曲壁蜂窝芯在指定频率范围内的传递率变化曲线.从传递率曲线可知曲壁蜂窝芯在505.25~645.75 Hz 的频率范围内有一定的隔振能力,以及在674.5 Hz 以上的高频范围内有显著的隔振作用.试验出现这种现象的原因为结构选用的材料PLA 是一种脆性材料,由PLA 制作的蜂窝芯具有很高的初始刚度,所以在低频阶段的隔振能力并不显著.但是试验发现这种脆性材料制造的结构在高频范围内有一定的隔振能力.

图19 曲壁蜂窝芯的传递率Fig.19 Transmissibility of curved-wall honeycomb core
试验测得的曲壁蜂窝芯的冲击响应如图20 所示,选取的波形为正弦波,脉冲峰值为8g,脉冲宽度为11 ms.从冲击加速度响应可以得出曲壁蜂窝芯具有较强的抗冲击能力,响应的最大峰值为5g较激励有了显著的降低,证实了曲壁蜂窝夹层板具有较强的抗冲击能力.
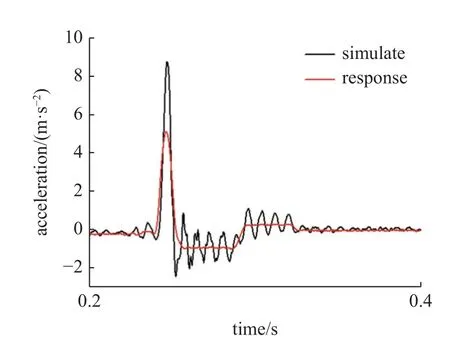
图20 夹层板在8g 正弦波激励下的响应Fig.20 Response of honeycomb sandwich plate excited by 8g sine wave
5 结论
本文推导了曲壁蜂窝的等效弹性参数,给出悬臂边界下曲壁蜂窝夹层板的动力学模型,利用Chebyshev-Ritz 方法研究夹层板的固有频率,并与有限元所得结果进行对比.利用增材制造的方法制作了曲壁蜂窝夹层板试件,利用振动台对试件进行了正弦扫频试验、谐波驻留试验和冲击实验,得出结论如下.
(1) 利用Chebyshev-Ritz 方法研究曲壁蜂窝夹层板是可行的,理论模型与有限元模型所求得的前5 阶固有频率误差在5%以内,在误差允许范围内,试验结果也验证了理论模型的正确性.
(2) 通过对曲壁蜂窝夹层板进行参数研究,发现随着蜂窝胞元壁厚的增加,蜂窝夹层板的前5 阶固有频率整体呈现减小趋势.随着单胞曲壁半径的增大,蜂窝夹层板的固有频率逐渐增大.当曲壁弧度在30°~75°的范围内,夹层板的固有频率随着曲壁弧度的增大而增大.
(3) 通过对曲壁蜂窝芯的隔振和冲击试验,可以发现曲壁蜂窝芯具有一定的高频的隔振能力,并且有较高的抵抗冲击性能,这将为蜂窝夹层结构在隔振和抗冲击方面的应用提供新的启示.
