混凝土多尺度应力响应方程及其数值模拟1)

2022-12-18李向南左晓宝周广盼黎亮

力学学报 2022年11期

李向南左晓宝周广盼黎亮

(南京理工大学理学院,南京 210094)

引言

混凝土是由水泥水化形成的净浆基体和砂、石等惰性骨料组成的多相多尺度复合材料,具有取材易、价格廉、性能高等优点,被广泛应用于桥梁、道路、铁路、港口、隧道、大坝和电站等各种基础设施工程中[1-2],准确地描述地震、强风、波浪和水流等各种载荷作用下混凝土内部的应力响应,是揭示混凝土材料失效破坏机理、评估基础设施工程服役安全性的基础[3-4].然而,载荷作用下,混凝土的受力特征和内部应力状态十分复杂,即使受到均匀外载荷作用,其内部也将产生复杂的不均匀空间应力场[5],这种复杂的应力分布可导致混凝土内微裂纹萌生与扩展、强度等力学性能退化[6-7].究其原因,混凝土中各组成材料的含量、几何形状、空间分布和力学性能差异较大,水化后所形成的内部结构在细观、亚细观、微观和纳观等尺度上的几何组成和物相性质明显不同,具有非均质和随机性[8].因此,根据混凝土在各尺度上材料的实际组成和物相性质,建立混凝土内多尺度应力响应与载荷作用之间的关系,对准确描述各种载荷作用下混凝土内不同尺度上的应力响应及其复杂的分布状态具有重要意义.

目前,人们根据混凝土材料的组成特点,利用多尺度方法,开展了混凝土弹性模量和泊松比等力学性能的理论预测及载荷作用下应力响应的分析研究.Ulm 等[9]将混凝土视为一种多相多孔复合材料,以各相材料的体积分数和刚度作为基本变量,建立混凝土在不同尺度上弹性模量和泊松比等力学性能的计算方法,但该方法将各相材料均等效为球形夹杂,不能准确反映各相材料几何形貌对混凝土力学性能的影响;Pichler 等[10]将水泥砂浆视为以净浆为基体相、细砂为夹杂相的复合材料,建立与水泥水化程度相关的砂浆力学性能计算模型,分析水泥水化过程中砂浆弹性模量和抗压强度的演变规律,但该模型没有考虑细砂的颗粒级配及其表层界面过渡区对砂浆力学性能的影响;Stora 等[11]根据水泥水化产物的微观形貌,将氢氧化钙、C-S-H凝胶等水化产物简化为理想的椭球体,建立了硬化水泥浆体弹性模量的计算模型,Termkhajornkit 等[12]在硬化水泥浆体弹性模量计算模型的基础上,计算了载荷作用下各水泥水化产物的应力响应,但他们的研究仅局限于硬化水泥浆体,没有考虑亚细观和细观尺度上骨料等夹杂相对砂浆和混凝土力学性能和应力响应的影响.Königsberger 等[13]将混凝土看作由砂浆、粗骨料及其界面过渡区ITZ 组成的复合材料,提出粗骨料及ITZ 应力响应的计算模型,但该模型没有考虑ITZ 力学性能和几何形状对其应力响应的影响,难以准确反映载荷作用下ITZ 的应力分布.综上,上述研究主要集中在硬化水泥浆体、砂浆和混凝土等水泥基材料弹性模量等力学性能的预测模型,较少涉及载荷作用下混凝土中各组成材料的多尺度力学响应问题,且现有的预测模型是以混凝土等水泥基材料中各组成材料的体积分数为基本变量,没有考虑它们的随机空间分布及相互作用,所获得的力学响应仅为混凝土等水泥基材料的平均值,未能反映材料组成空间中复杂的应力不均匀分布状态,难以描述混凝土在不同尺度空间上的应力集中现象及微裂纹萌生与扩展过程,不能用于分析混凝土材料的开裂损伤演化过程和失效破坏机理.针对现有模型中存在的上述不足,本文综合考虑混凝土多尺度组成材料的几何形状、颗粒级配、随机分布、相互作用和力学性能等多种因素,建立载荷作用下混凝土多尺度应力响应的分析模型.

为了合理描述载荷作用下混凝土内各尺度组成材料的受力特点及应力响应规律,首先,根据混凝土中各组成材料的尺度特征,重构混凝土各尺度复合材料的简化几何模型;其次,基于等效夹杂理论及混凝土多尺度组成特点,建立混凝土各尺度复合材料中基体相和夹杂相的应力响应方程;最后,以单轴压缩载荷作用下的混凝土细观组成为例,开展该载荷作用下混凝土中多尺度应力响应的数值计算,分析骨料空间位置和相互作用以及水化产物刚度、形状以及空间取向对其应力响应的影响.

1 混凝土几何模型重构

根据混凝土中各组成材料及其实际尺度特征[14],硬化后的混凝土主要由低密度和高密度C-S-H 凝胶相、氢氧化钙、毛细孔、细砂和粗骨料等材料组成,它们所组成的C-S-H 凝胶、硬化水泥浆体、水泥砂浆及混凝土的细观组成,分别处于纳观、微观、亚细观和细观尺度上[15],且各尺度材料均可视为由基体相和夹杂相组成的复合材料.在细观尺度上,将混凝土看作由水泥砂浆、粗骨料及其界面过渡区组成的复合材料,亚细观尺度上,水泥砂浆可视为硬化水泥浆体、细砂及其界面过渡区组成的复合材料,在微观尺度上,硬化水泥浆体由水泥矿物相、水化产物及毛细孔组成,而在尺寸更小的纳观尺度,C-S-H 凝胶又由低密度和高密度两种凝胶相组成,如图1 所示.

在混凝土各尺度上复合材料中,夹杂相的几何形状和空间分布,直接影响到载荷作用下混凝土在各尺度上的应力响应.为了获得夹杂相对混凝土中应力响应的影响,需要建立各尺度上复合材料的代表性体积单元,并重构相应的几何模型,做如下基本假定.

(1) 混凝土及其各尺度上的复合材料均为具有特征长度的周期性材料,且各尺度上的特征长度为夹杂相最大粒径的5 倍[16-17].

(2) 混凝土中各组成材料的几何形状,均简化为具有与其实际几何特征相对应的理想模型,如: 将粗骨料和细砂等效为球形夹杂,其表层界面过渡区等效为球壳形夹杂[18];将水泥中硅酸三钙(C3S)、硅酸二钙(C2S)、铝酸三钙(C3A)和铁铝酸四钙(C4AF)等矿物相以及毛细孔等效为球形夹杂,对于水化产物,将针棒状的C-S-H 凝胶和钙矾石(AFt)等效为长椭球形夹杂[11],将板状的氢氧化钙(CH)、水化硫铝酸钙(AFm)、水化铝酸钙(C3AH6)和水化铁酸钙(C3FH6)等效为扁椭球形夹杂[11];将低密度和高密度凝胶相等效为球形夹杂,如图1 所示.

图1 混凝土多尺度代表性体积单元Fig.1 Multiscale representation of concrete

(3) 在不同尺度上,混凝土各组成材料中的夹杂相均为各向同性材料[19],且水泥矿物相、水化产物及毛细孔等夹杂相的几何尺寸不同,但同一种夹杂相的几何形状及大小相同[10].

代表性体积单元中夹杂相的颗粒分布及其数量,是重构混凝土中各尺度复合材料几何模型的基本条件.

首先,在细观和亚细观尺度上,根据混凝土的配合比和粗、细骨料的颗粒级配,按照基本假定(1)和(2),确定混凝土细观组成和水泥砂浆代表性体积单元中粗骨料和细砂颗粒在不同粒径上的数量

式中,Nci和Nmi分别为粒径为rci和rmi的粗骨料和细砂的数量;f(rci) 和f(rmi) 分别为粗骨料和细砂的颗粒级配函数[20];wc,sc和ηs分别为混凝土的水灰比、砂灰比和砂率;ρc,ρw,ρs和 ρa分别为水泥、水、细砂和粗骨料的密度;Vc和Vm分别为混凝土细观组成和水泥砂浆代表性体积单元的体积.

其次,在微观尺度上,根据水泥水化机理[21]、水化反应方程[22]及基本假定(1)～ (3),硬化水泥浆体代表性体积单元中水泥矿物相、水化产物和毛细孔等夹杂相的数量可表示为

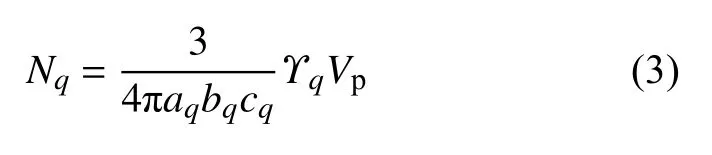
式中,N q为夹杂相q的数量;aq为夹杂相q的长半主轴,bq和cq为其短半主轴;Vp为硬化水泥浆体代表性体积单元的体积;Υq为夹杂相q的体积分数,可按文献[23]确定.

根据混凝土多尺度代表性体积单元中各夹杂相的几何形状及其数量,利用颗粒空间堆积方法[24-25],编制相应的MATLAB 计算程序PartilePacking.m,通过在混凝土各尺度代表性体积单元中随机投放相应的夹杂相,依次重构出混凝土细观组成、水泥砂浆和硬化水泥浆体的几何模型,该模型能反映混凝土内部不同尺度上基体相和夹杂相的几何形状和随机空间分布等组成特征,详见下文的“数值分析”.

2 等效夹杂模型

对于多相多尺度混凝土材料,其每一尺度上的复合材料在均匀载荷作用下,由于基体相和夹杂相力学性能的不同,不仅产生了均匀的远场应力,还在它们接触的边界面上产生不均匀的扰动应力,并在每一尺度上的复合材料中产生了不均匀的应力分布状态[26].因此,对于各尺度上的复合材料,其内部位置z处组成材料中应力和应变之间的关系,可表示为

式中,σ 和 ε 分别为复合材料中位置z处组成材料的应力和应变;ε0和 εpt,z分别为远场应力和扰动应力条件下复合材料位置z处的远场应变和扰动应变[27];Cz为复合材料位置z处的刚度张量,当基体相M和夹杂相I的刚度张量分别为C M和CI时,有

2.1 夹杂相本征应变

根据等效夹杂理论[28],当各尺度复合材料中夹杂相I内引入一个合适的本征应变时,该夹杂相I可等效为与基体相具有相同刚度的材料[29-30],如图2 所示.在引入夹杂相I 的本征应变后,式(4)可表示为

图2 等效夹杂理论示意图Fig.2 Schematic of equivalent inclusion theory

式中,χz表示复合材料内位置z处的特征函数

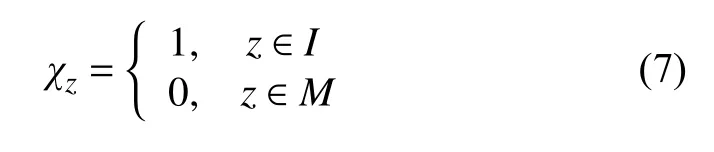
式(6)中,扰动应变 εpt,z与复合材料中所有夹杂相的本征应变 ε∗有关,二者之间满足

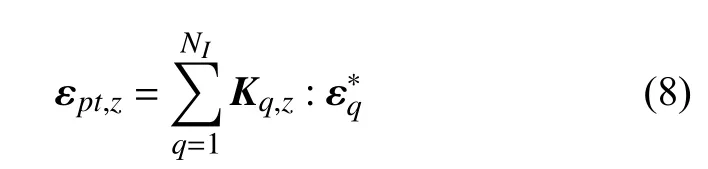
式中,NI为复合材料中夹杂相的数量;K q,z为任一夹杂相q的Eshelby 张量,由Eshelby 内部张量S和外部张量G组成[27],可表示为

由式(4)和式(6),可得

则以矩阵形式表示的式(10)为

式中,δij为Kronecker 记号;Pq,f表示全局坐标系下夹杂相q在夹杂域f内的极化张量,与该夹杂相在局部坐标系下的极化张量及其空间取向有关,Pq,f可表示为[31]

R为坐标变换矩阵,满足

式中，φ 为局部坐标系中x′轴与全局坐标系中x轴之间的夹角;ϑ 为局部坐标系中z′轴与全局坐标系中z轴之间的夹角,如图3 所示;Pq0,f为局部坐标系下夹杂相q的极化张量

图3 椭球体夹杂空间位置示意图Fig.3 Schematic of the spatial location of an ellipsoid inclusion

根据式(11),各尺度复合材料中夹杂相I 内的本征应变与其远场应变 ε0之间的关系,可表示为

2.2 应变响应

将式(8)和式(19)代入式(4),则各尺度上复合材料中位置z处的应变,可表示为

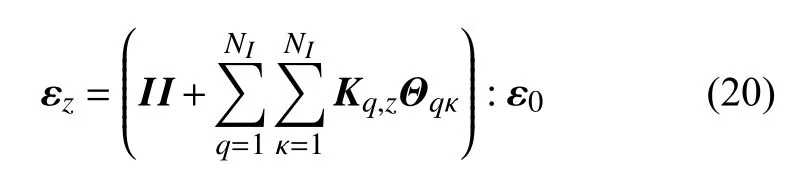
式中,II表示4 阶单位张量.

在单轴压缩载荷作用下,复合材料应变E与其内部各相材料应变 εz之间,满足

式中,〈 εz〉Ω表示复合材料空间域 Ω 内各组成材料应变的平均值.

将式(20)代入式(21),各尺度上复合材料中位置z处的远场应变 ε0与复合材料应变E之间,满足

将式(22)代入式(20),各尺度上复合材料中位置z处的应变可进一步表示为

式中,Az为各相材料与其所组成复合材料之间的应变转换张量

由式(23)可知,基体相M内的应变 εM为 εz|z∈M,夹杂相I内的应变 εI为 εz|z∈I,即

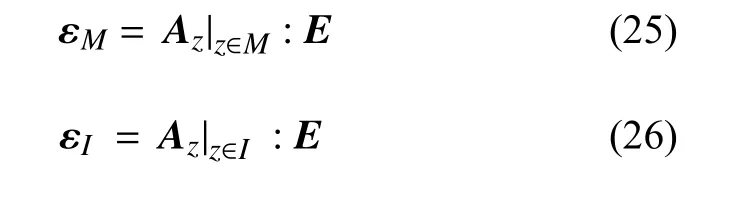
2.3 应力响应

单轴压缩载荷作用下,各尺度上复合材料所受到的应力与其基体相和夹杂相所受到的应力,满足

式中,Σ 为各尺度上复合材料所受到的应力;σq和σM分别为夹杂相q和基体相M所受到的应力.

将式(4)和式(23)代入式(27),可得

式中,Chom为复合材料的等效刚度张量

将式(23)和式(28)代入式(4),可获得复合材料中位置z处的应力

式中,σz为复合材料中位置z处的应力;Qz为各相材料与其所组成复合材料之间的应力转换张量

3 混凝土多尺度应力响应方程

式(32)和式(33)为载荷作用下混凝土内各尺度复合材料应力响应的一般表达式,没有考虑载荷作用所引起的力学响应在各尺度复合材料之间的联系与传递,不能具体确定混凝土内各尺度上的应力响应.因此,还需要进一步根据混凝土中不同尺度材料之间的组成关系,如图1 所示,建立混凝土内多尺度应力响应的计算方法: 从最低的纳观尺度出发,自下而上逐尺度依次确定C-S-H 凝胶、硬化水泥浆体、水泥砂浆和混凝土细观组成的等效刚度,即混凝土各尺度复合材料等效刚度的升阶计算;再根据载荷作用下混凝土应力由高尺度向低尺度的传递规律,从最高的细观尺度出发,自上而下逐尺度依次确定混凝土细观组成、水泥砂浆、硬化水泥浆体和CS-H 凝胶中的应力响应,即混凝土各尺度复合材料应力响应的降阶计算.

3.1 等效刚度的升阶计算

3.1.1 纳观和微观尺度

纳观尺度上,以低密度和高密度凝胶颗粒为夹杂相,二者组成的C-S-H 凝胶为基体相,如图1(d)所示,根据式(29),该尺度上C-S-H 凝胶的等效刚度,可表示为

式中,kLD,kHD和 µLD,µHD分别为低密度和高密度凝胶颗粒的体积模量和剪切模量;J和K分别为4 阶单位张量的偏差部分和体积部分[32].

在该尺度上,根据C-S-H 凝胶的结构组成特点,本文忽略低密度和高密度凝胶颗粒空间位置及其相互作用对C-S-H 凝胶力学性能的影响[33],仅考虑其在C-S-H 凝胶中所占体积分数,则式(34)可化简为

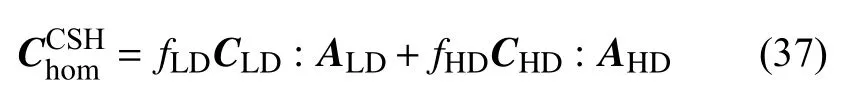
式中,fLD和fHD分别为低密度和高密度凝胶颗粒的体积分数,与水泥矿物相中C3S 和C2S 的水化程度相关,可按文献[33]确定.

微观尺度上,以水泥矿物相、水泥水化产物和毛细孔为夹杂相,它们所组成的硬化水泥浆体为基体相,如图1(c)所示,则根据式(29),可获得硬化水泥浆体的等效刚度张量

式中,kq和 µq分别为硬化水泥浆体中夹杂相q的体积模量和剪切模量.

3.1.2 亚细观和细观尺度

亚细观尺度上,以细砂及其界面过渡区为夹杂相,硬化水泥浆体为基体相,如图1(b)所示,而细观尺度上,以粗骨料及其界面过渡区为夹杂相,砂浆为基体相,如图1(a)所示,则根据式(29),可获得亚细观尺度砂浆和细观尺度混凝土的等效刚度

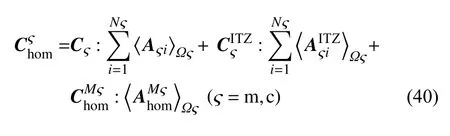
根据基本假定(3),细砂或粗骨料颗粒及其表层界面过渡区的刚度张量,可表示为

由硬化水泥浆体、砂浆和混凝土细观组成的等效刚度,可获得其体积模量、剪切模量和弹性模量

3.2 应力响应的降阶计算

细观和亚细观尺度上,粗骨料、细砂及其表层界面过渡区等夹杂相的存在,改变了混凝土细观组成和砂浆中的应力分布,使它们的基体相和夹杂相所受到的应力差异较大.根据式(32)和式(33),可获得混凝土细观组成和砂浆中基体相和夹杂相的应力

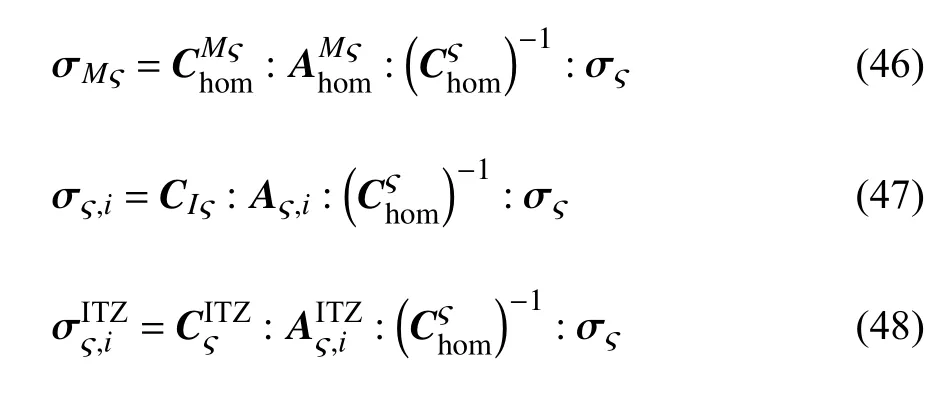
式中,σς和σMς,σIς,i及分别为混凝土细观组成或砂浆和它们的基体相、第i个粗骨料或细砂夹杂相及其表层界面过渡区所受到的应力.

类似地,微观和纳观尺度上,水泥矿物相、水化产物、低密度和高密度凝胶为夹杂相,它们所受到的应力与硬化水泥浆体和C-S-H 凝胶等基体相存在较大的应力差,按照式(32)和式(33),可得

式中,σq为微观尺度上硬化水泥浆体中夹杂相q所受到的应力;σCSH为微观尺度上C-S-H 凝胶所受到的应力;σLD和 σHD分别为纳观尺度上低密度和高密度凝胶相所受到的应力.

4 数值实现

4.1 与有限元结果对比

根据本文所建立的混凝土等效夹杂模型和多尺度应力响应方程,本文运用MATLAB 语言,编制了相应的计算程序Mul-ScaleConStress.m,程序框图如图4 所示.该程序可基于混凝土的配合比和各组成材料的力学性能等参数,计算混凝土在细观、亚细观和微观等尺度上各组成材料的应力状态.考虑到混凝土多尺度微结构的复杂性,难以通过实验直接测量混凝土在各尺度上的应力分布,本文采用通用的有限元软件ABAQUS,模拟单轴压缩载荷作用下混凝土细观组成中基体相(水泥砂浆)和夹杂相(粗骨料及其表层界面过渡区)中的应力分布,并与程序Mul-ScaleConStress.m 的计算结果进行对比分析.

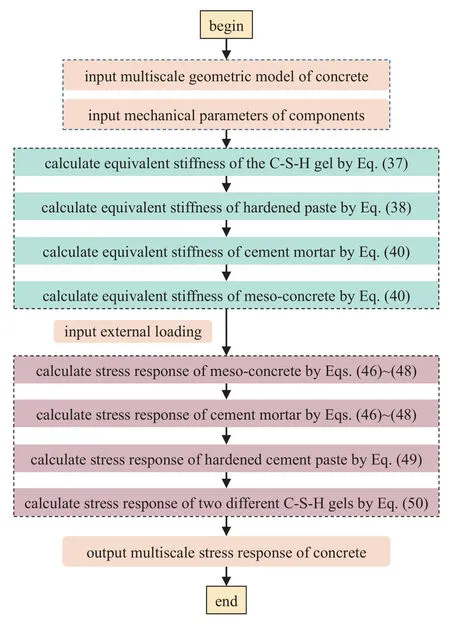
图4 混凝土多尺度应力响应的计算框图Fig.4 Flowchart for calculating multiscale stress response of concrete

数值计算时,所选取混凝土细观组成的几何尺寸为100 mm × 100 mm × 100 mm,沿z轴方向作用有均布载荷−10 MPa.各粗骨料球心均在截面A-1(y=50 mm)上,其粒径分别为7 mm 和5 mm,界面过渡区厚度为500 μm[36].ABAQUS 建模时,采用二次四面体单元划分网格,界面过渡区的网格尺寸为0.5 mm,砂浆和粗骨料的网格尺寸为2 mm,并对局部网格尺寸进行细化,如图5 所示.砂浆、粗骨料及其界面过渡区的弹性模量分别为20,70 和16 GPa,泊松比分别为0.20,0.16 和0.20[37],体积模量分别为11.1,34.3 和8.9 GPa,剪切模量分别为8.3,30.2 和6.7 GPa.

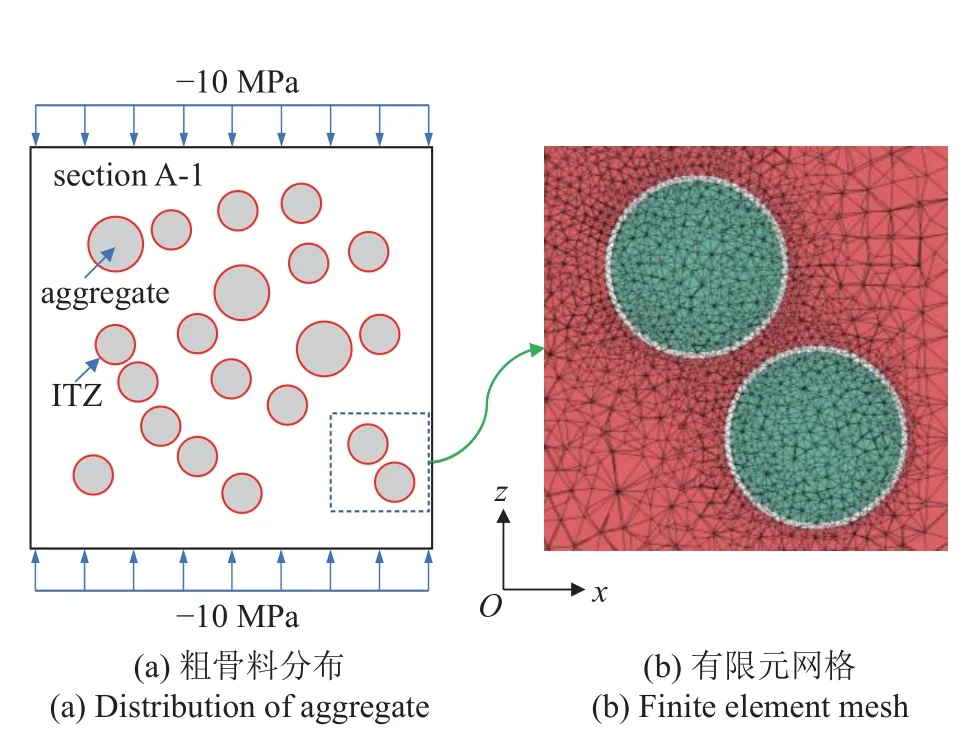
图5 混凝土的细观组成Fig.5 Meso-concrete

图6 给出了单压载荷作用下混凝土细观组成截面A-1 上不同位置处应力分布的程序计算值和有限元解.由图可知,砂浆、粗骨料及其界面过渡区应力分布的程序计算值和有限元解基本一致,说明本文所建立的混凝土多尺度应力响应方程,能较好地分析载荷作用下混凝土内组成材料的应力响应.

图6 截面A-1 上应力分布的程序计算值和有限元数值解Fig.6 Program calculation value and finite element solution of stress distribution on section A-1

4.2 数值分析

为了分析载荷作用下混凝土的多尺度应力响应,以水灰比、砂灰比和砂率分别为0.55,2.00 和0.37 的混凝土为研究对象,其中,水泥选用P·I 42.5硅酸盐水泥,其密度和比表面积分别为3150 kg/m3和390 m2/kg,水泥颗粒的最大粒径为100 μm,水泥中CaO,SiO2,Al2O3,Fe2O3,MgO,SO3,K2O 和Na2O 所占百分比分别为62.00%,20.30%,5.00%,2.20%,3.20%,2.60%,0.70%和0.30%.粗骨料的最大和最小粒径分别为20 mm 和5 mm,细砂最大和最小粒径分别为5 mm 和0.15 mm,界面过渡区厚度为500 μm,粗骨料和细砂的表观密度分别为2600 kg/m3和2500 kg/m3,它们的连续级配曲线如图7 所示.模型中,混凝土各组成材料的力学参数如表1 所示,粗骨料和细砂表层界面过渡区的体积模量和剪切模量取硬化水泥浆体体积模量和剪切模量的40%[20].

表1 混凝土中各组分的力学参数Table 1 Mechanical parameters of components in concrete

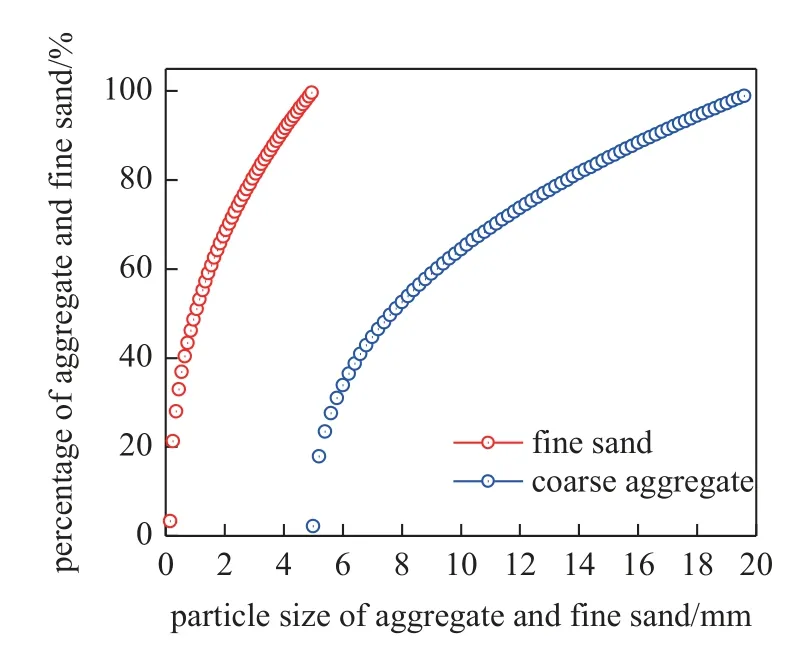
图7 粗骨料和细砂的连续级配曲线Fig.7 Continuous gradation curves of aggregate and fine sand

根据上述混凝土的配合比和粗、细骨料的颗粒级配,利用本文所编制的PartilePacking.m 计算程序,依次重构出混凝土的多尺度几何模型,如图8 所示;再以单轴压缩载荷作用为例,在标准养护28 d 后的混凝土细观组成外部z方向施加均布载荷 −10 MPa,利用所编制的Mul-ScaleConStress.m 计算程序,分析了养护过程中混凝土各尺度复合材料的弹性模量和载荷作用下混凝土的多尺度应力响应.

图8 混凝土多尺度几何模型Fig.8 Multiscale geometric model of concrete

图9 给出了混凝土细观组成、水泥砂浆和硬化水泥浆体弹性模量随养护时间的变化规律.由图可知,它们的弹性模量均随养护时间的增加而逐渐增大,且其增长速度逐渐减慢.这是因为,养护期间水泥矿物相发生水化反应,使得硬化水泥浆体中水化产物含量逐渐增加、孔隙率逐渐降低[35],而水化产物的弹性模量明显高于毛细孔的弹性模量,进而导致硬化水泥浆体的弹性模量逐渐增加.由于水泥水化是一个养护前期速度较快、后期速度减慢的过程[38],受此影响,硬化水泥浆体弹性模量的时变过程也呈现这一规律.作为亚细观尺度上水泥砂浆的基体相,硬化水泥浆体弹性模量的增加使得水泥砂浆的弹性模量随之增加,同理,水泥砂浆弹性模量的增加也使得混凝土细观组成的弹性模量随之增加[39].此外,图9 给出了忽略粗骨料颗粒间相互作用情况下混凝土细观组成弹性模量的时变规律.由图可知,相比于考虑粗骨料颗粒间相互作用,忽略该作用时混凝土细观组成弹性模量的计算值偏低.

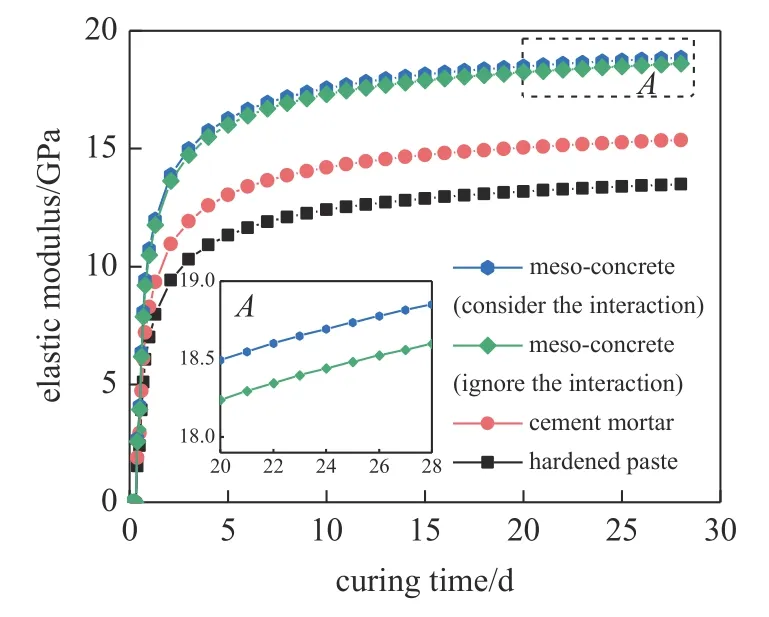
图9 混凝土细观组成、水泥砂浆和硬化水泥浆体弹性模量随养护时间的变化规律Fig.9 Time-varying elastic modulus of meso-concrete,cement mortar and hardened cement paste

图10(a)给出了混凝土细观组成截面A-2 (y=50 mm)上粗骨料颗粒及其界面过渡区的分布情况,其中,灰色表示粗骨料颗粒,红色表示粗骨料外部界面过渡区,白色表示砂浆基体相.图10(b)和图10(c)给出了单轴压缩载荷作用下该截面上各组分z和x方向上正应力的分布.由图可知,单轴压缩载荷作用下,粗骨料内所受应力为均布应力,而砂浆基体相所受应力与粗骨料颗粒的空间位置相关.在粗骨料颗粒附近,可观察到应力集中现象[40],根据应力的分布特征,可将粗骨料外部划分为上、下位置和左、右位置等两个区域,如图10(a)所示.混凝土细观组成中各组分z方向的正应力均为压应力,且在该方向上,粗骨料上、下位置处砂浆所受应力明显大于其左、右位置处砂浆所受应力;在x方向上,粗骨料颗粒上、下位置处砂浆所受正应力为压应力,而粗骨料内部及其左、右位置处砂浆所受正应力均为拉应力.此外,在远离粗骨料颗粒处,砂浆中的应力分布较为均匀,如区域C所示,而在粗骨料颗粒聚集处,砂浆同时受到多个粗骨料应力扰动的影响,其应力分布有明显波动,如区域D所示.

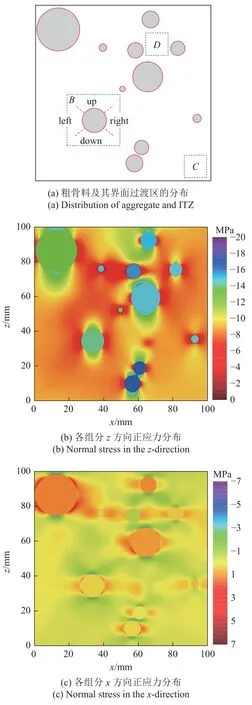
图10 截面A-2 上各组分的空间分布和应力分布Fig.10 Spatial and stress distribution of each component on section A-2

图11 给出了截面A-2 上区域B内不同位置处各组分的应力分布.由图可知,粗骨料-砂浆界面过渡区内正应力方向(拉或压)的变化规律与水泥砂浆相一致.界面过渡区的存在对粗骨料颗粒左、右位置处x和y方向的正应力以及上、下位置处z方向的正应力影响较小,但使得其左、右位置处z方向的正应力明显降低,上、下位置处x和y方向的正应力明显增加.由该区域内各组分应力的分布特征可知,粗骨料颗粒、界面过渡区和水泥砂浆均处于三向受力状态,粗骨料上、下位置处界面过渡区和水泥砂浆的应力状态为三向受压,粗骨料内部及其左、右位置处界面过渡区和水泥砂浆的应力状态为两拉一压.该区域内粗骨料及其左侧界面过渡区和水泥砂浆在x,y,z3 个方向上的正应力分别为(0.3,0.4,−14.1)、(0.1,1.6,−0.7)和(0.1,1.6,−2.2).由此可知,相比于界面过渡区和水泥砂浆,该位置处粗骨料颗粒的应力状态最为不利,但由于界面过渡区的力学性能远低于砂浆和粗骨料[37],界面过渡区反而最容易发生破坏,并产生平行于载荷作用方向的微裂缝[13].

图11 区域B 内粗骨料及其周围组分的应力分布Fig.11 Stress distribution of coarse aggregate and its surrounding components in region B

以亚细观尺度上的水泥砂浆(区域C处)为例,给出了考虑或忽略细砂(细骨料)间相互作用情况下细砂颗粒中的正应力分布,分析了细砂间相互作用对细砂颗粒中应力分布状态的影响,如图12 所示.由图可知,细砂颗粒间相互作用对其应力分布的影响程度与二者间的距离和相对位置有关.当保持细砂颗粒间的相对位置(z方向夹角为0°)不变,增加其距离时,细砂颗粒中z方向的正应力先逐渐降低后趋于稳定,而x和y方向的正应力先逐渐增加后趋于稳定.由各方向上正应力趋于稳定的位置可知,细砂颗粒间相互作用的有效影响范围约为颗粒半径的6 倍.当保持细砂颗粒间的距离(与细砂粒径的比值为1.5)不变,改变其相对位置,即二者在z方向的夹角时,可以发现,随着z方向夹角的增加,细砂颗粒中y和z方向的正应力先逐渐降低后基本不变,而x方向的正应力先有所降低后逐渐增加.当细砂颗粒间z方向的夹角为0°～ 40°时,二者的相互作用使得细砂中z方向的正应力明显增加,反之,则略有降低;当z方向夹角为15°～ 60°时,二者的相互作用使细砂中x方向的正应力明显降低,反之,则明显增加.

图12 细砂中应力随颗粒间距和相对位置的变化Fig.12 The change of normal stress in fine sand particles with the distance and relative position

以微观尺度上的硬化水泥浆体为例,分析了其内部水泥矿物相及其水化产物z和x方向上正应力随与z轴间夹角的变化规律,如图13 所示.计算时,选取未受细砂颗粒应力扰动影响的硬化浆体,即其

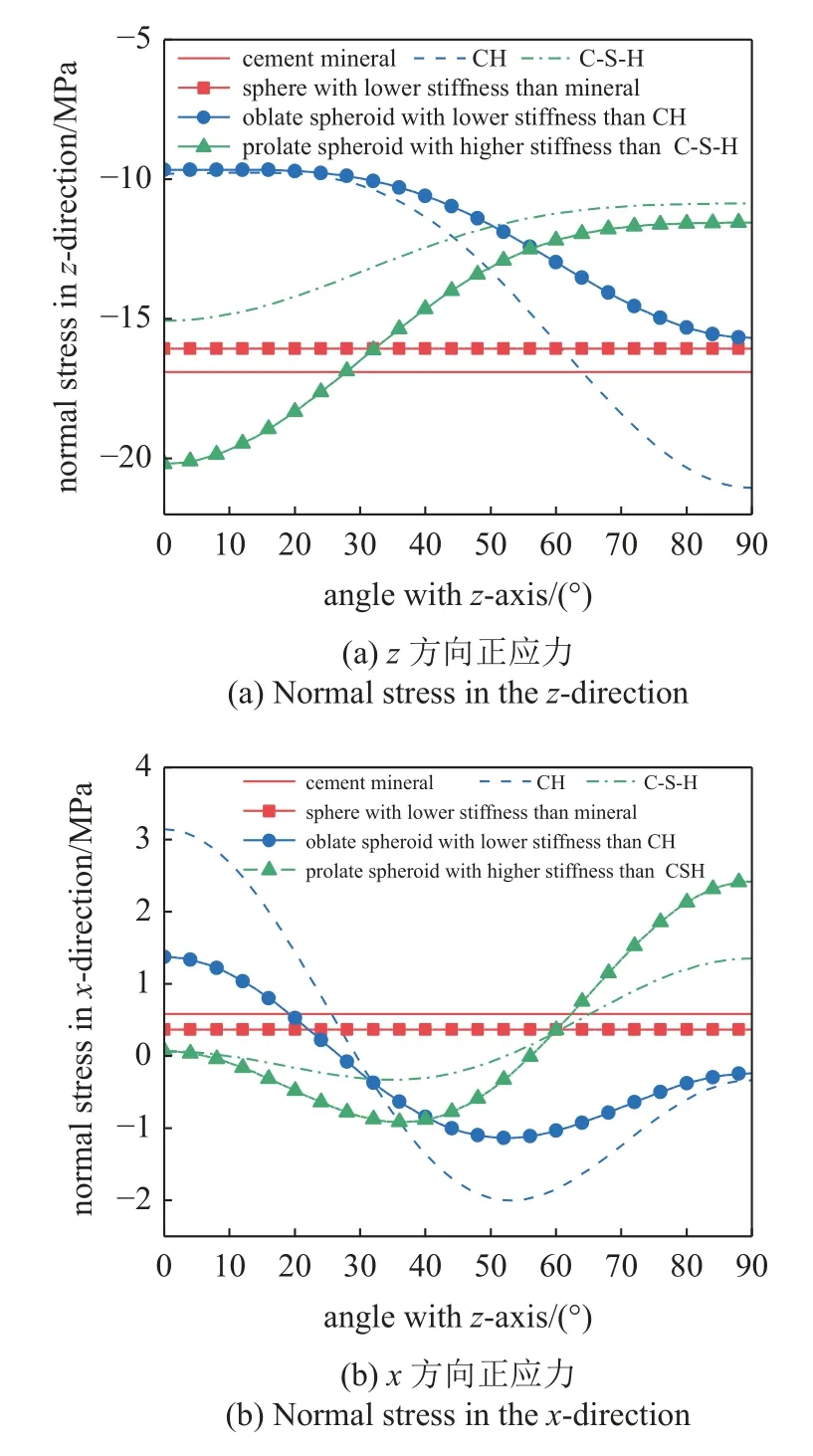
图13 硬化水泥浆体中水泥矿物相及其水化产物所受应力Fig.13 The stress in the cement mineral phase and hydration products in hardened cement paste

在x,y,z方向的所受应力分别为0,0,−10 MPa,以便于分析各组成材料刚度、几何形状和空间取向对其应力响应的影响.其中,C-S-H 凝胶和AFt 半长轴与半短轴的比值 (a/b)分别取15 和20,CH,AFm,C3AH6和C3FH6的该比值均取0.10[12].由图可知,球形水泥矿物相和椭球形水化产物的刚度越大,其x和z方向的正应力也越大.球形水泥矿物相所受应力与其空间取向无关,椭球形水化产物则有关,具体为与载荷作用方向(z轴)的夹角越小,长椭球形水化产物z方向的正应力越大,扁椭球形与之相反;与z轴间夹角为0°时,球形水泥矿物相和椭球形水化产物x方向的正应力均为拉应力,随着夹角的增加,长椭球形水化产物x方向正应力由拉应力变为压应力,且压应力先增加后逐渐降低,当压应力降低至0 时,该应力转变为拉应力,并逐渐增加;扁椭球形水化产物x方向正应力的变化规律与长椭球形类似,但其受最大拉应力和压应力的夹角位置与长椭球形不同,具体为 C-S-H 凝胶x方向上受最大拉应力和压应力的夹角位置分别为90°和35°,氢氧化钙受最大拉应力和压应力的夹角位置则分别为0°和55°.