基于分形理论和Mori-Tanaka 方法的颗粒土渗透注浆加固体性能预测方法及应用1)

彭 鹏 彭 峰 孙振宇 张顶立,2)

* (北京交通大学城市地下工程教育部重点实验室,北京 100044)

† (北京瑞威铁道工程技术有限公司,北京 100038)

引言

诸如砂土、砂卵(砾) 石等颗粒土地层是由块石、细粒土和孔隙构成的松散岩土介质系统[1-2].作为一种常见的不良工程地质条件,当对此类土体进行隧道开挖时,由于其具有施工难度大、地层扰动强的特点,极易引发塌方等工程事故[3].为了提高隧道的稳定性,降低隧道施工和运营期的安全风险,注浆作为一种可以有效封堵围岩裂隙,填补围岩内部孔洞的工程措施得到了广泛的应用[4-6].由于隧道围岩组成成分多样、构造方式复杂,且注浆项目具有隐蔽性等特点[7],导致注浆后形成的加固体的力学性质难以准确获得,注浆加固机理的研究落后于工程实践[8].针对实际工程遇到颗粒土类型的不良地质条件,通过分析注浆前后围岩的细观结构特征和宏观力学性质,开展注浆加固后加固体力学性能的预测研究,可以充分指导注浆设计,具有重要的研究意义.

为此,学者们针对颗粒土注浆后形成的加固体的性能开展了诸多研究.邓成进等[9]利用室内静力大三轴试验研究了注浆后堆石料的宏观力学性质,得到了级配特征、围压和粗颗粒含量对注浆后堆石料力学性质的影响规律.沙飞等[10]则以砂土介质为研究对象,基于室内模型注浆实验结果,利用方差分析法,研究了注浆材料、砂土级配和注浆压力三个敏感因素对被注介质进行加固后的28 d 强度的影响程度.许宏发等[11]对注浆前后破碎岩体的强度实验值进行了无量纲分析,利用非线性拟合分析提出了28 d 强度与水灰比之间的经验公式和破碎岩体注浆加固体强度增长率的经验公式.以上研究利用宏观试验,分别以堆石料、砂石和破碎岩体为研究对象,分析了不同因素对注浆加固后加固体强度的影响,但忽略了地层的组分和构造的多样性,缺乏对注浆加固体力学性质的微观机理分析,所得结论的适用范围较小.雷进生等[12]基于随机分形理论和物性参数关联的特点,开发了可用于浆液在地层中的扩散形态的精确模拟和注浆后加固体的力学性质准确预测的数值方法.将地层和浆液分别作为复合材料的基体和夹杂,Chao 等[13]基于分形理论描述了含有圆形孔隙的二维平面多孔介质的几何特征,并利用平均场均质方法和Mori-Tanaka 方法预测了多孔介质强度,预测结果与试验结果吻合程度良好.Naili 等[14]则基于有限元分析,针对短纤维增强复合材料,利用无偏估计分析了不同均值化方法计算复合材料强度的准确性,得到了两级均质化方法对于短纤维增强复合材料强度预测准确度最高的结论.以上研究强调了地层力学性质的不均匀性,但在模型中都采用了二维多孔介质作为研究对象,在将地层孔隙抽象为复合材料夹杂的过程中,忽略了地层孔隙的连通性和迂曲效应,而孔隙的连通性和迂曲效应是导致隧道围岩空间变异性[15]的主要因素,其会造成围岩承载不均匀,并进一步影响支护结构力学响应[16].此外,这些研究由于没有建立起加固体力学性能和隧道围岩空间变异性之间的有效联系[17],也就无法对具有强烈的空间变异性的注浆围岩开挖时的宏观力学响应进行分析,所得的结论不能直接指导隧道注浆加固.

为了有效指导隧道注浆加固,本文采用分形理论描述隧道围岩作为三维多孔介质状态下的孔隙特征,基于迂曲度经验公式建立了地层体孔隙率和面孔隙率的转换关系.结合Mori-Tanaka 方法,以体孔隙率为变量,提出新的注浆加固体的宏观刚度预测方法.假设注浆加固体的不同破坏模式,以面孔隙率为基础,利用能量法求解注浆加固体的强度.最后,利用本文提出的注浆加固体性能预测方法对注浆后的玉京山隧道回填体进行地层参数赋予,建立可以考虑注浆围岩空间变异性的有限差分模型,并分析注浆前后围岩变形和支护结构力学响应.

1 注浆加固体的刚度和强度预测方法

1.1 孔隙地层的分形介质理论描述

将颗粒土地层抽象为含有足够多数量的连通孔隙的地层代表单元的多孔介质,其中孔隙的直径大小和空间分布为随机分布,如图1(a)所示,地层代表单元的yOz平面如图1(b)所示.对于含有孔隙的地层平面,分形理论提供了一种有效的方法来量化由于分形对象在不同尺度上重复其自身结构所导致的不规则特征[18].对于含有大量孔隙的土层系统,已有大量研究表明孔隙半径与孔隙数量之间的关系符合分形理论[19].

图1 孔隙地层代表单元Fig.1 Represent element of pore soil

将地层作为分形体时,其内部孔隙的直径大小L′和累计数量N(L′ ≥λ) 存在如下幂函数分布关系

其中,λmax是孔隙的最大直径,λ是指定的孔隙直径,Df是孔隙分布的分形维数.因此,总孔隙数量可以表示为

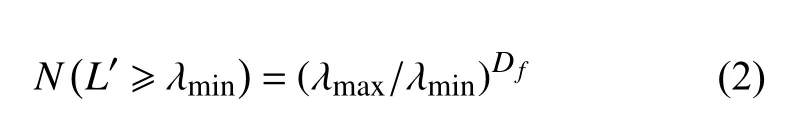
其中,λmin为孔隙的最小直径.现有研究[20-21]给出了以分形理论计算得到的孔隙面积Ap为

其中,φs为面孔隙率.将代表单元中的孔隙等效为含有相同数量且平均直径为的孔隙,此时有孔隙面积为

将式(2)代入式(4),并联立式(3),可解得等效后代表单元内部孔隙的平均直径

式(1)～式(5)基于分形理论求解了孔隙的平均直径,将孔隙地层的代表单元均质化为含有相同数量的直径为的孔隙地层.由于各个连通孔隙的迂曲长度不相同,导致同一地层中的体孔隙率与面孔隙率并不相等[22].为了计算孔隙的迂曲长度,假设某单相饱和流体由左向右流通孔隙地层代表单元,Δp为沿流通方向两侧压力差,Am为代表单元截面积,L为代表单元在流动方向上的长度,Le为流动路径长度,其该单相饱和流体的运动规律符合达西定律.定义迂曲度为[23]

由Hagen-Poiseuille 公式计算的考虑通道迂曲时的通道流量q为

此外,根据Darcy 定律计算通道流量为

其中,k为渗透率,μ为流体黏度.由体孔隙率定义,有

φv为体孔隙率.联立式(7)～式(9)可得

此外,Koponen 等[24]基于格子玻尔兹曼方法导出了平均迂曲度和体孔隙率之间的关系,为

联立式(10)和式(11),得到

式(12)建立了体孔隙率和面孔隙率及渗透系数之间的关系.

1.2 考虑注浆填充率的注浆加固体刚度预测方法

基于单夹杂问题,对多夹杂复合材料有效模量进行研究.首先求解在主轴坐标系下基体与夹杂之间力学行为的局部化关系,然后将主轴坐标系下得到的物理量转化为多夹杂问题中宏观坐标(x1,x2,x3)下的物理量.取只含有一个椭球型夹杂的土体单元为研究对象,如图2 所示.分别将土体和孔隙视作基体和夹杂,并假设基体和夹杂为各向同性材料,从而将孔隙地层作为复合材料进行研究.椭球型夹杂内部的点,有

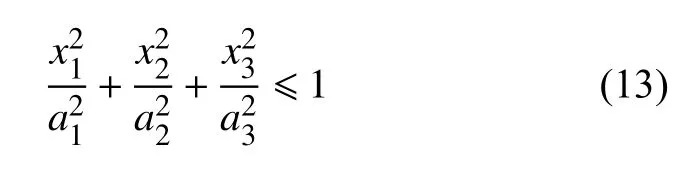
图2 单夹杂受到远场均匀应变模型Fig.2 Single inclusion subjected to far-field uniform strain model

式中,a1,a2,a3分别为沿方向的轴长度,对于待加固地层中的连通孔隙,可以认为是一种长纤维型结构,即在椭球型夹杂的情况下a2=a3=0,a1=∞.在地层中为空间随机分布,分布密度函数可以表示为γ(θ,η),其中θ为x1坐标轴和x1′坐标轴之间的空间夹角,η为x2和′之间的空间夹角.

对于主轴坐标系下的单夹杂问题,Eshelby 对于含有单夹杂代表单元V在边界əV上作用远场均匀应变时,单元内应变进行了求解.通过引入模量张量为的均匀线弹性比较材料,单夹杂在均匀应变作用下,域内个点处的应变可以由Green 函数表示为统一的形式.取基体材料为线弹性比较材料,并用G1,K1和v1分别表示夹杂的剪切模量、体积模量和泊松比.考虑到椭球型夹杂域外的集体材料与比较材料之间的刚度差δCjpkl(x)为0,基于均匀性和各向同性假设,在椭球型夹杂域内夹杂材料与比较材料的刚度差δCjpkl(x)为一常数.可将代表单元内任意一点的应变解析表达式改写为

沈观林等[25]说明了在远场应变均匀的情况下,椭球型夹杂内的应变ɛkl(x)也是均匀的,可以将椭球型夹杂内的平均应变改写为

其中,I是四阶单位张量,为基体的平均应变,张量P的定义为

Mori-Tanaka 方法[26]对于多夹杂问题进行求解时,将单夹杂问题中远场应变作为复合材料基体的平均应变,则椭球型夹杂的平均应变可以改写为

在浆液渗透填充多孔介质的孔隙空间过程中,地层中的一部分孔隙被充填密实,而另一部分孔隙空间并未充填并仍然保留了孔隙结构.因此,本文引入注浆填充率α,其物理意义为在多孔介质渗透注浆过程中,有αφv的孔隙空间被浆液充填,注浆填充率的宏观表现即为地层填充率.根据平均场均质化方法,对于由土体、浆液填充的孔隙空间及剩余孔隙空间构成的三相复合材料,基于1.1 节的结果,其平均应变可以表示为

其中,Tw=(I+PδCw)−1,当脚标w为g或p时,分别代表注浆填充后的孔隙和未被浆液填充的孔隙.将上式代入式(18),可以得到椭球型夹杂内的平均应变为

因此,利用Mori-Tanaka 方法计算得到的主轴坐标系下,进行注浆后形成的加固体的强度的估计可以表示为

其中,Mw=[δCw−1+(1−φv)P]−1,当脚标w为g或p时,分别代表注浆填充后的孔隙和未被浆液填充的孔隙.式(22)基于Mori-Tanaka 方法建立了多夹杂问题中,夹杂具有统一空间取向的局部化关系.但在实际工程中,孔隙地层中的连通孔隙在地层中随机分布,利用式(23)计算夹杂的空间角度平均[25]

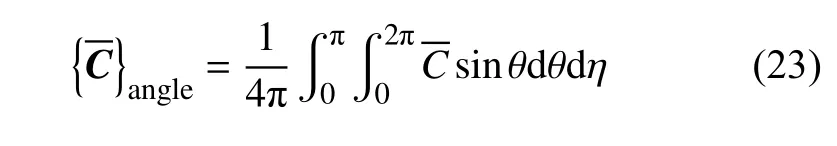
将式(22)代入式(23)后,由于假设基体和夹杂均为各向同性材料,因此空间角度平均前后刚度矩阵的表达式一致,可得

利用本文方法得到的渗透注浆加固后的体积模量和剪切模量分别表示为

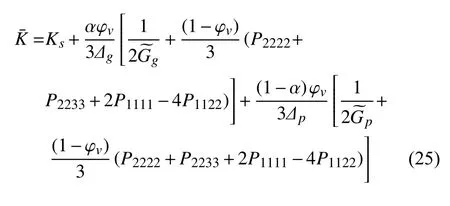
其中,当脚标w为g或p时,分别代表注浆填充后的孔隙和未被浆液填充的孔隙.张量P各分量为[27]

1.3 考虑注浆填充率的注浆加固体强度预测方法

由于在进行注浆加固体刚度预测方法的研究过程中,随机分布的地层连通孔隙已经通过平均迂曲度,平均孔隙直径和平均空间取向计算进行了均质化处理,在开展含有多个长纤维型夹杂复合材料的强度预测研究时,可以假设其内部空间基体材料和夹杂均匀分布.夹杂宽度为h,两个夹杂之间的宽度为2b,上下两端受到沿长纤维夹杂方向的均布力σf.则由复合材料的微观结构可以看出,长纤维夹杂的屈曲破坏是导致复合材料破坏的基本形式.当夹杂的屈曲半波彼此相反时,复合材料宏观表现为横向拉伸破坏,如图3(a)所示,而当夹杂的屈曲半波相同时,复合材料受压破坏时的宏观表现为剪切破坏形式.如图3(b)所示.

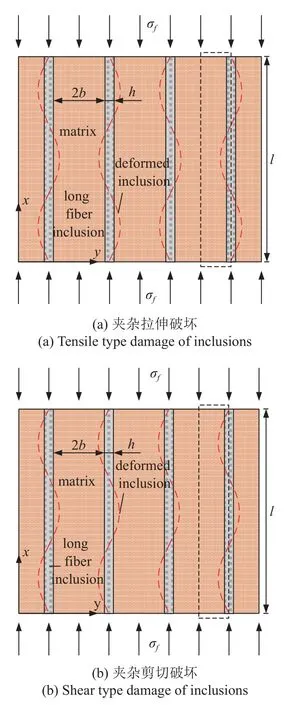
图3 夹杂破坏形式Fig.3 Damage characteristics of inclusions

注浆填充的孔隙作为长纤维型夹杂,其单条孔隙宽度h远小于基体宽度b,因此在计算过程中将夹杂作为杆件,而将基体作为板,u和v分别为夹杂沿x和y方向的位移.当对边简支板受到均布载荷时,由板壳理论[28]可知其板内沿y方向的位移v可以由单三角级数表示为

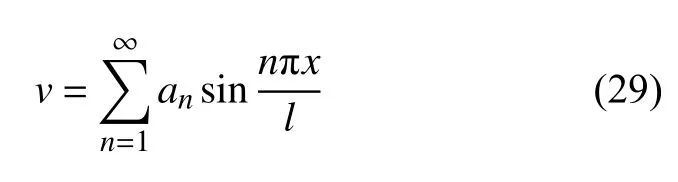
取宽度为b的基体和一个夹杂作为基本单元,复合材料具有周期性结构,其面孔隙率αφs可以表示为

基体的水平位移ɛy0可以表示为ɛy0=v/b,则σy0=Etv/b,其中Et为基体抗拉强度,基体应变能则表示为

夹杂作为杆件时的应变能可以表示为

夹杂在外力P=σfh作用下的外力功可以表示为

根据狄利克雷稳定性判据,应变能与外力功差值的一阶变分等于0 可得屈曲极限载荷为

假设第m个正弦波时,P取得最小值

取σf的极小值为夹杂的破坏强度

因此复合材料的抗压强度为

由于注浆后的土体中E1≫Et,化简式(37)

当夹杂屈曲半波形态相同时,复合材料宏观表现为横向剪切破坏,如图4(b)所示.仍然取宽度为b的基体和一个夹杂作为基本单元,基体的剪应变是应变能的主要成分,基体的剪应变γxy0为

图4 玉京山隧道地质及水文情况Fig.4 Geological and hydrological conditions of the Yujingshan tunnel

由于基体水平位移与y无关,可以得到基体沿水平方向的应变为

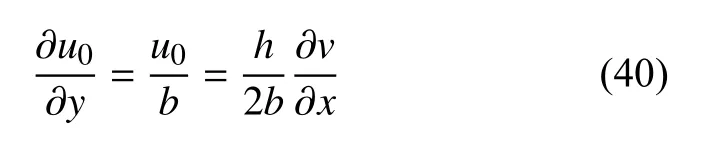
将式(40)代入式(39),可得

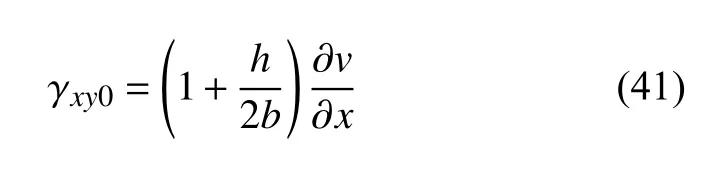
因此,基体的剪切应变能为

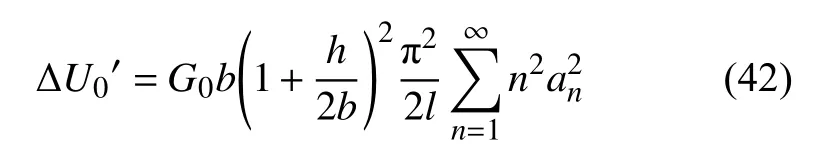
横向剪切破坏时,夹杂的应变能和外力功没有变化,仍可由式(32)和式(33)分别表示,采用相同方法可以得到

许宏发等[11]通过总结不同学者开展的注浆后加固体性能试验结果,提出了单轴抗压强度增长率的概念,其定义为

其中,Sca和Scb分别为注浆后和注浆前的土体单轴抗压强度.并给出了单轴抗压强度增长率ζc和黏聚力增长率ζcoh,内摩擦角增长率ζf之间的关系

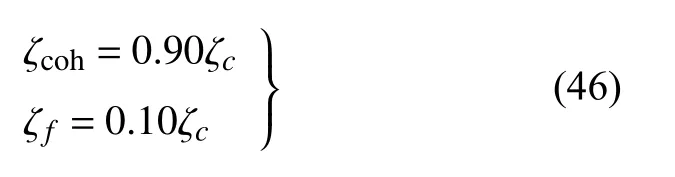
2 工程应用

将本文提出的注浆后加固体性能预测方法应用于玉京山隧道,建立可考虑注浆后围岩空间变异性的数值模型,分析注浆和不注浆时围岩位移和支护结构力学响应.

2.1 工程背景

玉京山隧道位于云南省昭通市威信县境内,是成贵高铁的控制性工程.隧道全长6306.28 m,为设计最高时速250 km/h 的单洞双线隧道.线路设计为30‰单面上坡,最大埋深为350 m,隧道洞身主要穿越煤系地层和可溶岩地层.2016 年7 月,玉京山隧道横洞工区向小里程端掘进时,发现开挖面前方存在一个巨型溶洞大厅,如图4(a)所示.溶洞大厅沿线路方向发育约100 m,垂直于线路发育约230 m.在岩溶大厅左侧拱脚处灰岩层中发育有玉京山暗河,暗河全长18 km,与隧道大里程方向呈58°交角,暗河入口处和出口处观察到的最大地下水流量分别为5.0 m3/s 和21.16 m3/s.暗河分布位置如图2(b)所示.

在溶洞回填阶段,按照由低到高,由两侧到中间的施工顺序开展溶洞回填,为保证回填地层能够尽量提供承载能力,回填面每3 m 采用机械平整压实.为了溶洞壁渗出的地下水能够有效排放,在距离溶洞壁3 m 范围内采用块石进行回填,块石直径不小于0.3 m,溶洞其余部分则采用弃渣进行回填.根据叶堃[29]和王莹[30]对玉京山隧道地质和水文条件的调查,玉京山隧道周边围岩的平均孔隙率和渗透系数分别为0.15 和40.5 nm/s,按照式(47)换算为渗透率

其中,k为渗透率,Kp为渗透系数,μw为水的黏度系数2.98 mPa·s,g为重力加速度.换算可得,地层的渗透率为123 μm2.回填材料的物理力学性质和渗透参数如表1 所列.

表1 回填材料的力学性质和渗透参数Table 1 The mechanical property and penetration parameter of backfill material

在隧道暗挖阶段,根据地层条件和施工现场限制,采用三步法或四步法进行开挖.围岩物理力学参数和支护结构参数根据勘察资料确定.如表2 和表3所示.

表2 围岩及支护物理力学参数Table 2 Physico-mechanics parameters of surrounding rock and support

表3 支护参数Table 3 Parameters of support

由于采用物理力学性质较差的工程弃渣回填巨型溶洞,在隧道开挖导致的应力重分布过程中难以承担相应的载荷.此外,由于溶洞形状的不规则性导致回填体在隧道单侧分布,或隧道断面上某一侧溶洞面积远大于另一侧时,支护结构将产生严重的应力集中现象.为此,采用边墙注浆的方式对工程弃渣回填区域进行加固,而加固后形成的注浆加固体的性能,则是影响隧道围岩和支护结构稳定性的控制因素.

2.2 考虑围岩空间变异性的数值模型建立方法及验证

现有研究[31]表明,孔隙是决定地层物理力学性质的主要因素,本文假设溶洞回填弃渣中的固体相具有相同的强度和刚度,待加固区域内的土体单元的孔隙率符合高斯分布,弃渣回填溶洞地层的强度及刚度的空间变异性主要由不同位置处的孔隙率不相同所导致.由现场调查得到的待加固地层平均孔隙率为0.15,为了使得随机赋予的孔隙率能够覆盖实际地层中可能存在的孔隙率值,将0.225 作为孔隙率标准差,此时孔隙率处于(0,0.45)范围内的概率为65.63%.故此,本文假设地层中孔隙率分布为N(0.15,0.225).利用Flac3D进行二次开发,在开挖程序中,遍历开挖步范围内的所有单元,判断该单元是否属于待注浆区域,对于处于待注浆区域内的土体单元,利用高斯分布函数生成大小范围为(0,0.6),且符合N(0.15,0.225)分布的随机数作为弃渣回填区域单元的体孔隙率,利用式(5)计算得到单元体内的平均直径,利用式(12)生成相对应的面孔隙率,基于体孔隙率,采用式(25)和式(26)分别求解该单元的体积模量,剪切模量,以面孔隙率为基础,利用式(38)、式(43)和式(44)计算单元的单轴抗压强度,最终利用式(46)求得单元的黏聚力和内摩擦角,并将计算得到的物理力学性质赋予该单元,程序设计流程如图5 所示.

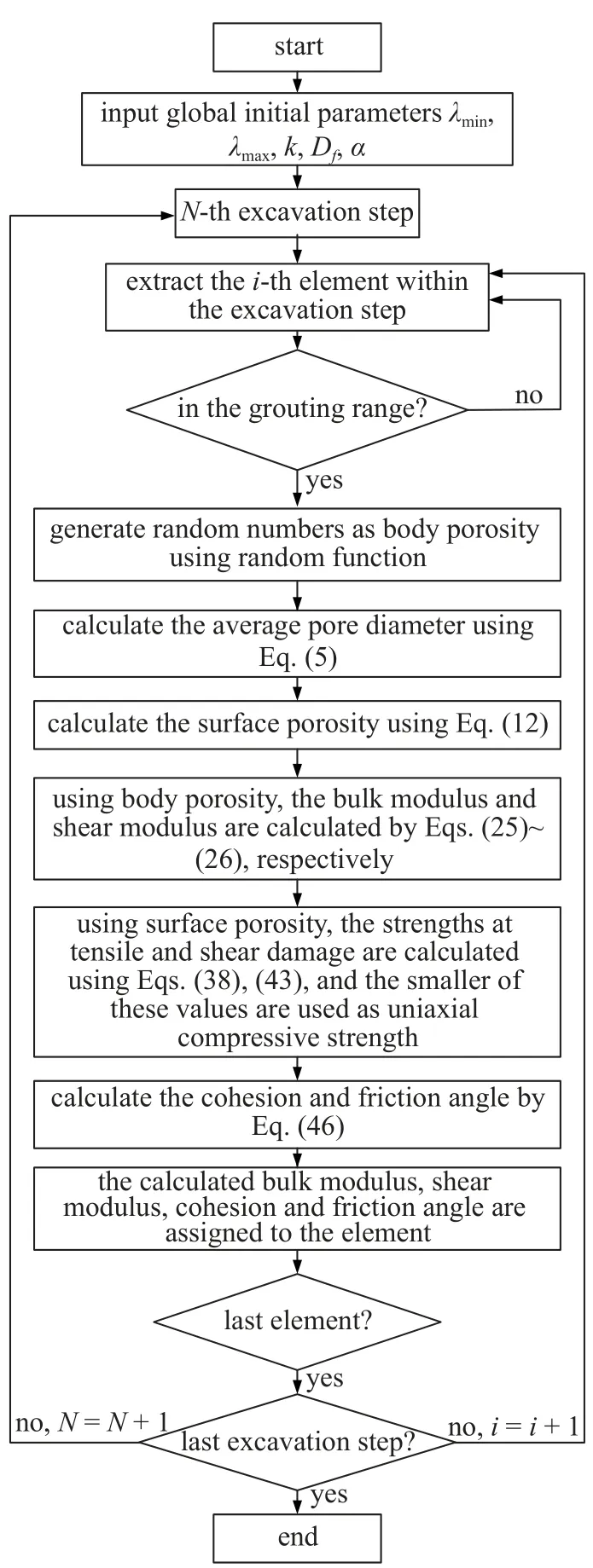
图5 程序设计流程Fig.5 Program flow chart

利用该数值模型建立方法实现弃渣回填地层物理力学性质的空间变异性模拟,最终形成的三维模型如图6 所示.

图6 数值模型及其构造Fig.6 Numerical model and its construction

当孔隙率为0.1～0.6 时的地层物理力学参数预测值如表4 所列.

表4 不同孔隙率下注浆加固体力学性质预测值Table 4 The prediction value of mechanical property of grouted reinforced body under different porosity

在注浆过程中,将注浆压力和浆液流量作为单孔终止注浆的依据.当注浆压力达到设计终止压力并维持5～10 min,即可结束注浆.而当实际浆液流量达到设计浆液流量的1.5 倍,注浆压力仍达不到设计终止压力时,应通过加大水玻璃配比调节浆液凝胶时间,使得压力达到设计终止压力,结束注浆.工程现场采用的注浆参数如表5 所列.

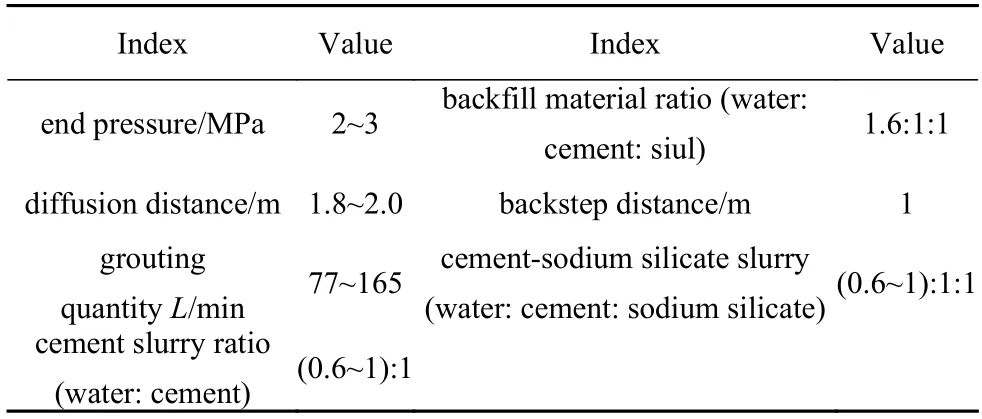
表5 渗透注浆参数Table 5 Penetration grouting parameters

在玉京山隧道边墙注浆过程中,D3 K279+888断面的单液浆和双液浆注入量分别如表6 所列.地层填充率反算公式

表6 D3 K279+888 断面注浆记录Table 6 Grouting record of D3 K279+888 section

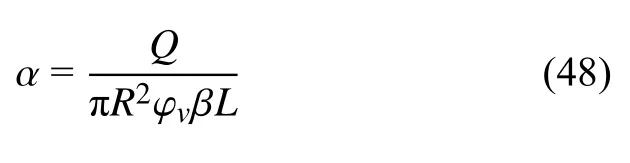
其中,β为浆液消耗系数,Q为注浆量,L为注浆孔的长度,R为浆液扩散半径.可以得到,实际注浆填充率为0.71.

计算注浆填充率为0.71 时的隧道洞身水平收敛,并与现场监测结果对比如图7 所示.可以看出,模拟实测结果在上台阶和中台阶水平收敛中均表现出‘急速增长—缓慢增长′的发展趋势,上台阶和中台阶的误差值分别为31.4%和9.5%.数值模拟和现场监测得到的下台阶水平收敛则表现出先急速增长,后缓慢增加,最终达到稳定状态的变化特征,下台阶收敛实测值与模拟值之间的误差为20.62%.上、下台阶产生了较大误差的原因为实际工程中上、下台阶处的围岩受地下水软化作用较大,导致上台阶水平收敛的实测值较大.然而,三个台阶的误差绝对值较小,最大值仅为8 mm,表明利用本文方法建立的模型可以准确模拟隧道围岩和支护结构的力学响应.

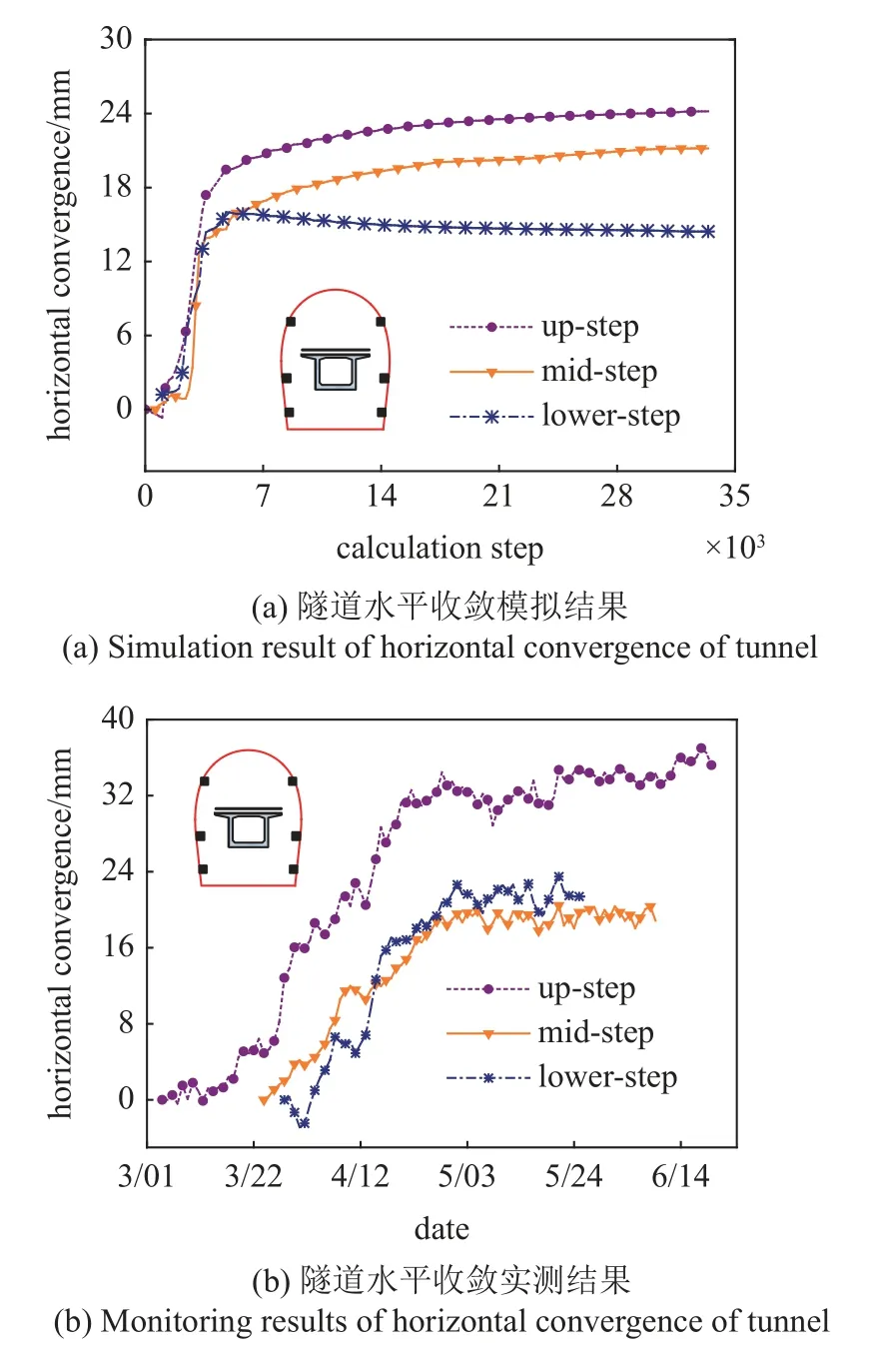
图7 D3 K279+88 断面水平收敛模拟值和实测值对比Fig.7 Comparison between simulation and monitoring result of horizontal convergence of D3 K279+888 section

2.3 注浆和未注浆时的围岩位移和支护结构力学响应分析

分别对未注浆和注浆的围岩位移和支护结构力学响应进行分析.图8(a)为未注浆时的围岩位移,箭头指向为位移方向.可以看出,在未注浆直接开挖隧道时,回填体中A,B两个区域产生了较大的变形,A区域中C点变形最大,为228.71 mm.与此同时,A区E点处也产生了较大的底板隆起,为72.46 mm,这是由于工程弃渣自身的物理力学性质较差,隧道开挖导致围岩应力发生释放,较小的载荷导致A区围岩产生较大位移.B区域内最大位移发生在D点处,为52.55 mm,B区产生较大位移的原因为回填体与溶洞壁之间为接触连接,而回填体内的位移累计效应导致了B区域内回填体与溶洞壁之间的连接不紧密,产生了脱空情况,导致B区发生类似于滑坡现象的位移发展模式.图8(b)为注浆时的围岩位移,可以看出,位移较大的区域仅在隧道底部F区产生,其最大位移发生在H点处,为19.18 mm.采取注浆加固措施时,未注浆时A区边墙处的对应的A′区围岩位移均小于15 mm,降低了50%～90%.未注浆时B区滑坡区域对应的B′区域围岩位移均小于5 mm,表明注浆加固有效地控制了围岩位移发展,并且避免了由于围岩位移累计导致的远端滑坡现象的发生.

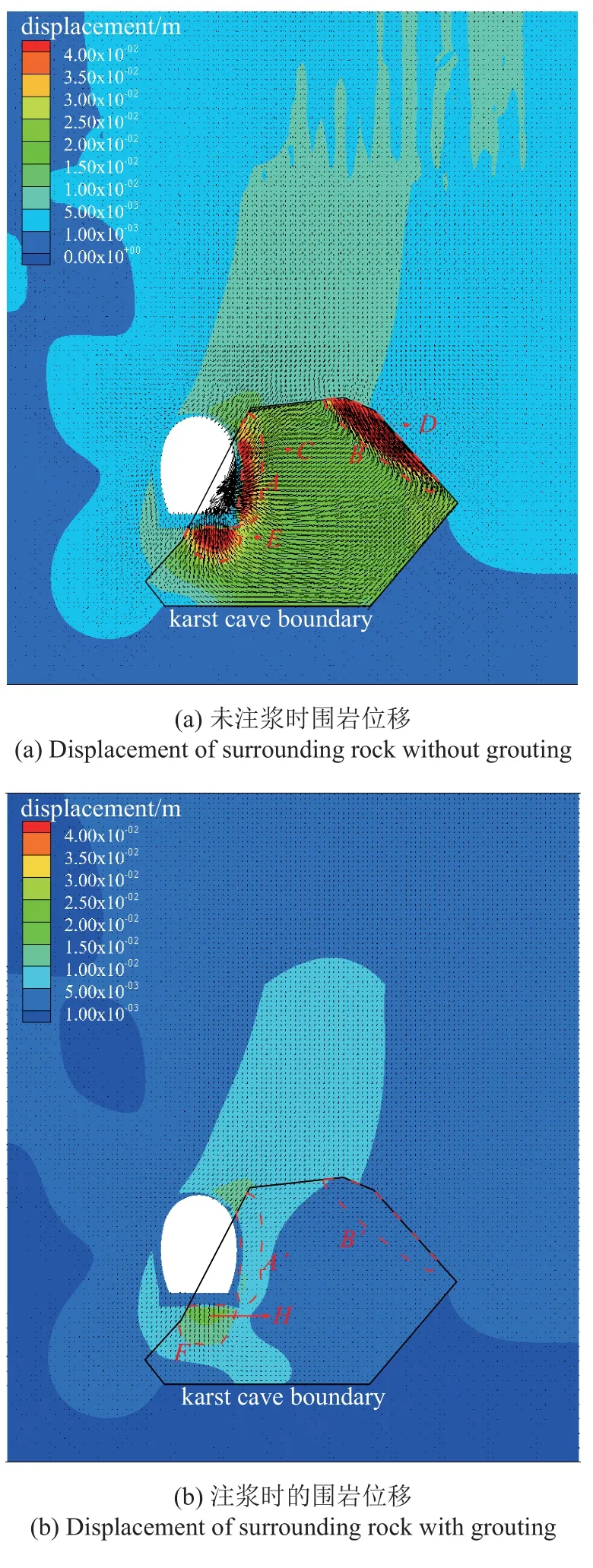
图8 注浆和未注浆时围岩位移(Y=20 m 断面)Fig.8 Displacement of surrounding rock with and without grouting(Y=20 m section)

图9 为未注浆时和注浆时Y=20 m 断面的支护结构的力学响应,其中,K点和M点为溶洞边界与隧道初支的交点.利用溶洞边界将支护结构划分为三个区域,一是溶洞边界左上侧区域,其围岩由物理力学性质较好的灰岩构成,为灰岩区域;二是溶洞边界右下侧区域,其围岩主要由物理力学性质较差的压密回填土构成,为回填区域;三是接触点K和M点附近的区域,接触点两侧的围岩物理力学性质相差较大,为接触区域.

图9(a)为注浆和未注浆时Y=20 m 断面支护结构弯矩分布.可以看出,在未注浆时回填体区域内对应的初支结构产生了较大弯矩,其中最大弯矩发生在隧道底部,为−143.19 kN·m,与此同时,右侧拱脚处也产生了较大的弯矩,为−43.58 kN·m.在接触区域内,支护结构弯矩发生了较大突变,其中,K点周围的最大正弯矩和最小负弯矩分别为95.53 kN·m和−24.53 kN·m,M点周围的最大正弯矩和最小负弯矩分别为64.97 kN·m 和−36.36 kN·m,表明接触区域附近产生了较大的剪力导致支护结构弯矩发生了剧烈变化.采取注浆措施时,隧道底部回填区域内的支护结构上的弯矩几乎为0,弯矩较大的位置主要发生在接触区域内和右侧拱脚处,其中,接触区域K点处的最大正弯矩和最小负弯矩分别为121.84 kN·m 和−33.48 kN·m,接触点M附近仅产生正弯矩,其值为36.02 kN·m,右侧拱脚处的最大负弯矩为−49.65 kN·m.采取注浆措施时,初支结构弯矩分布在灰岩和回填区域内更为平均,但在接触区域内的弯矩变化也更加剧烈,表明在接触点附近的剪力进一步增大.

图9(b)为Y=20 m 断面支护结构扭矩分布.可以看出,灰岩区域内支护结构承受的扭矩较小,几乎为0.在接触区域和回填体区域内产生了较大的扭矩,最大负扭矩发生在隧道右侧拱脚处,为−79.73 kN·m,在接触区域内M点附近产生的最大正扭矩,为66.27 kN·m.在现行的隧道支护设计方法中往往忽略掉扭矩的影响,而在含有回填溶洞区域进行隧道开挖时,由于回填体物理力学性质软弱,导致支护结构受力复杂,产生了不可忽略的扭矩.

图9(c)为Y=20 m 断面支护结构变形.在回填体区域内,隧底区域产生最大变形为24.31 mm,右侧拱腰处的位移为18.24 mm.在接触区域内的K点附近产生的最大变形则为15.56 mm.隧底区域和K点附近产生较大变形的原因主要为围岩的物理力学性质软弱导致承载力不足,支护结构承受较大载荷.在拱腰处产生较大变形则是由于右侧拱墙相对于水平方向的载荷为梁式受载构件,拱墙的梁效应导致拱腰处产生了较大挠度.采取注浆措施时,由于回填区域内的围岩物理力学性质提高,支护结构变形得到了较大改善,在接触区域K点附近产生了小于10 mm 的支护变形.

图9(d)为Y=20 m 断面支护结构最大主应力分布,其中负值表示受压.可以看出,未注浆时,灰岩区域产生了较大的最大主应力,最大值发生在左侧拱肩位置为−17.40 MPa,而在回填区域内的最大主应力较小,最大值仅为−5.77 MPa.采取注浆措施时,在接触区域内,K点和M点周围的最大主应力分别为−5.55 MPa 和−7.81 MPa.这是由于支护结构滞后施作,在围岩应力重分布的过程中,灰岩区围岩和回填区围岩对载荷进行分配,支护结构并不参与围岩载荷分配,尽管进行了注浆加固,但仍不足以改变灰岩区和回填区围岩的载荷分配规律,灰岩区仍承受较大载荷.当支护结构施作后,灰岩区域的支护结构上产生了较大的最大主应力.接触区域内接触点两侧刚度不匹配,产生的较大剪力导致最大主应力较大.

图9 注浆和未注浆时支护结构力学响应(Y=20 m 断面)Fig.9 Mechanical response of support structures with and without grouting (Y=20 m section)

3 结论

利用分形多孔介质理论和经验迂曲度公式求解了面孔隙率和体孔隙率之间的关系.以体孔隙率作为变量,提出了注浆后加固体的刚度预测方法.结合能量法,以面孔隙率为变量,建立了拉伸形破坏和剪切型破坏两种不同破坏模式下的单轴抗压强度预测公式.以玉京山隧道为工程背景,通过将待加固区域内的土体单元的孔隙率赋予符合正态分布的随机数,并利用提出的预测方法计算得到每一土体单元的力学参数,对注浆和未注浆时围岩位移和支护结构力学响应进行分析,得到了以下结论.

(1)将地层中的连通孔隙假设为长纤维型夹杂,通过引入注浆填充率,基于Mori-Tanaka 方法建立了新的注浆加固后加固体刚度预测模型.该模型考虑了注浆填充率对注浆加固体的性能参数的影响,因此可以考虑地层孔隙对加固体刚度的削弱和注浆加固对加固体刚度的增强效应.

(2)通过假设不同长纤维型夹杂间的屈曲半波形式,得到加固体存在拉伸型破坏和剪切型破坏两种破坏模式,并利用能量法求解了两种破坏模式下的注浆加固体单轴抗压强度,并建立了注浆加固体强度的理论预测模型.

(3)通过将待注浆区域的回填土单元,利用本文模型计算并赋予相应的地层物理力学参数,实现了三维状态下注浆围岩物理力学性质空间变异性的模拟.利用本文提出的注浆加固体性能预测模型建立玉京山隧道数值模型,上下台阶的横洞水平收敛最大绝对误差值仅为8 mm,中台阶的最终收敛相对误差值仅为9.5%,充分验证了本文方法的准确性.

(4)未注浆时,在围岩性质较差的右侧边墙和隧道底部出现了较大围岩位移,在回填体远端产生类似滑坡的围岩变形模式.围岩性质较差区域对应的支护结构上产生了较大的弯矩和不可忽略的扭矩,初支位移最大为24.31 mm,围岩性质较好区域对应的支护结构上产生了较大的最大主应力.注浆加固可降低约50%～90%的围岩变形,有效控制了回填体区域对应的支护结构弯矩,降低支护结构上的扭矩至0,控制支护结构的变形发展至10 mm 以内.此外,由于灰岩和回填土之间的物理力学性质相差过大,注浆加固难以改变不同区域围岩应力重分布规律,导致支护结构上的最大主应力分布改善幅度较小.