完全催化壁驻点高超声速流动加热地面模拟方法研究
2018-04-25聂春生黄建栋徐晓亮曹占伟
聂春生, 黄建栋, 徐晓亮, 曹占伟
(中国运载火箭技术研究院 空间物理重点实验室, 北京 100076)
0 引 言
临近空间高超声速飞行器驻点区气动加热量是工程设计的重要参数,高超声速飞行空气经过激波压缩和边界层摩擦后,气流的能量将发生很大的变化,能量在气体粒子平动、转动、振动、电子激发等微观自由度之间的分配将重新进行调整,空气中主要的组元会发生不同的化学反应,从而致使气体的物理化学特性和气体流动规律的发生变化[1]。高温气体化学反应流在防热材料表面上主要的传热有温度梯度引起的能量输运与不同焓值组元质量扩散引起的能量输运两项[2],不同的化学反应流状态对上述两种传热行为的大小不同,能量在温度梯度输运和组元质量扩散之间可以互换,而材料表面对应化学反应流动具有一定的催化作用,不同的防热材料催化特性不同,会影响本来到达防热材料表面的化学反应进程,从而影响气动加热大小。由于传统弹道式再入飞行器气动加热主要来源40km以下,气流基本处于化学平衡状态,防热材料表面催化特性对气动加热特性影响并不显著,国内关于材料表面催化特性的研究相对薄弱,相关报道较少。而随着近年来高超声速飞行器研究热潮的兴起,飞行器表面催化特性对气动热环境及热响应特性的影响越发显著,材料表面催化特性测试及评价相关研究需求也愈发迫切,尤其是欧美各国的飞行试验、基于风洞流场重构的CFD 仿真结果均表明:一些状态下,驻点区域完全催化表面的热载荷甚至达到完全非催化表面热流的2~3倍,在非驻点区域,完全催化表面的热载荷也可较完全非催化表面热流高12%~50%。例如:日本“OREX”[3]高超声速飞行器CFD 预测的完全非催化壁驻点热流是完全催化驻点热流的50%;美国“Space Shuttle”[4]高超声速飞行器迎风面热流分布CFD预测结果与飞行试验结果表明:材料表面催化特性对飞行器迎风面气动热载荷的影响比大钝头体飞行器更加严重。
高温非平衡流动及表面催化对临近空间高超声速飞行器表面的气动加热的影响要显著和重要的多[5-6],需要精确预示和在地面充分考核。目前可以在地面高焓风洞中研究化学反应流动,此类风洞主要模拟气体焓值和热流,目前常用的高焓设备有高频等离子体风洞、电弧风洞、高焓激波风洞等,这些风洞原理不同,但一个共同特点是喷管出口来流本身是非平衡流场,与真实飞行环境下的来流空气存在差别,使得即使风洞来流的能量等级与飞行条件下气流能量等级相同,但地面风洞中,有大量的能量被冻结在流体中,作为离解的原子组分的生成焓,这部分气体的能量是否会释放到模型表面取决于模型表面材料的催化特性[7- 11]。
飞行器头部驻点区是气动加热和化学反应流动最严重的区域,也是高超声速飞行器地面热考核的关键部位。如何在地面高焓风洞条件下模拟驻点区真实飞行条件下的空气化学反应流动加热,将直接影响到地面风洞对飞行环境的考核程度。本文通过平衡边界层驻点加热Fay-Riddell公式及冻结边界层驻点加热公式Goulard公式,推导出地面风洞试验模拟驻点热流的关键参数,针对完全催化壁驻点建立了三参数模拟准则,并针对不同尺寸的球头模型和某典型地面风洞来流条件,采用数值模拟的方法对模拟准则进行了数值验证。
1 驻点加热的影响参数分析
平衡边界层驻点热流依据Fay-Riddell公式确定[12]:
qs= (α/Cp)s(he-hw)·
(1)
冻结边界层驻点热流依据Goulard公式确定[13]:
qs= (α/Cp)s(he-hw)·
[1+(Le2/3φ-1)hDht-hw]
(2)

(4)
其中:(α/Cp)s为驻点换热系数,hD为离解焓;Cp为定压比热容;hw为壁面焓;ce、cw分别为空气离解组元N和O原子在边界层外缘和壁面的质量浓度。
针对Fay-Riddell公式:

(5)
针对Goulad公式:
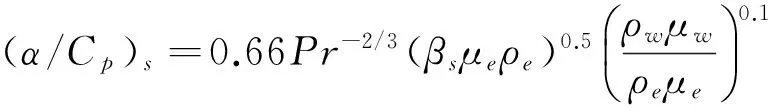
(6)
在Le=1(Le=Pr/Sc)的近似下,平衡边界层驻点热流与冻结边界层驻点热流公式可近似为:
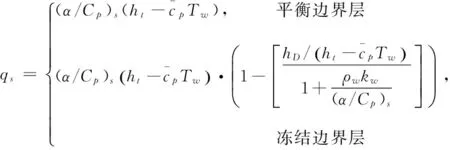
(7)
对于平衡边界层,影响驻点热流的流场参数有驻点换热系数(α/Cp)s和总焓ht两个参数。
对于冻结边界层,当材料一定(即材料壁面催化特性确定)时,影响驻点热流的流场参数是驻点换热系数(α/Cp)s、总焓ht、离解焓hD三个参数。
在高超声速条件下,边界层内驻点线上压力梯度为零(dp/dy=0),即边界层外缘压力与物面压力(驻点压力ps)相等,因此边界层外缘气体密度ρe和物面气体密度ρw分别由驻点压力ps、总焓ht以及表面温度Tw控制。由此可见,影响驻点换热系数(α/Cp)s的流场参数有:驻点压力ps、驻点速度梯度βs、总焓ht。
因此,影响驻点热流的流场参数转换为:驻点压力ps、驻点速度梯度βs、总焓ht和离解焓hD四个参数,其中前三个参数对化学平衡和冻结边界层驻点热流均有影响,而离解焓hD与物面催化反应速率常数Kw相互耦合影响化学冻结边界层的驻点热流。
对于冻结边界层驻点,依据Goulard公式,当Kw=0时(“完全非催化”表面),其完全非催化表面热流定义为qn,当Kw=∞时(“完全催化”表面),离解能在物面完全释放,其完全催化表面热流定义qf。

(9)
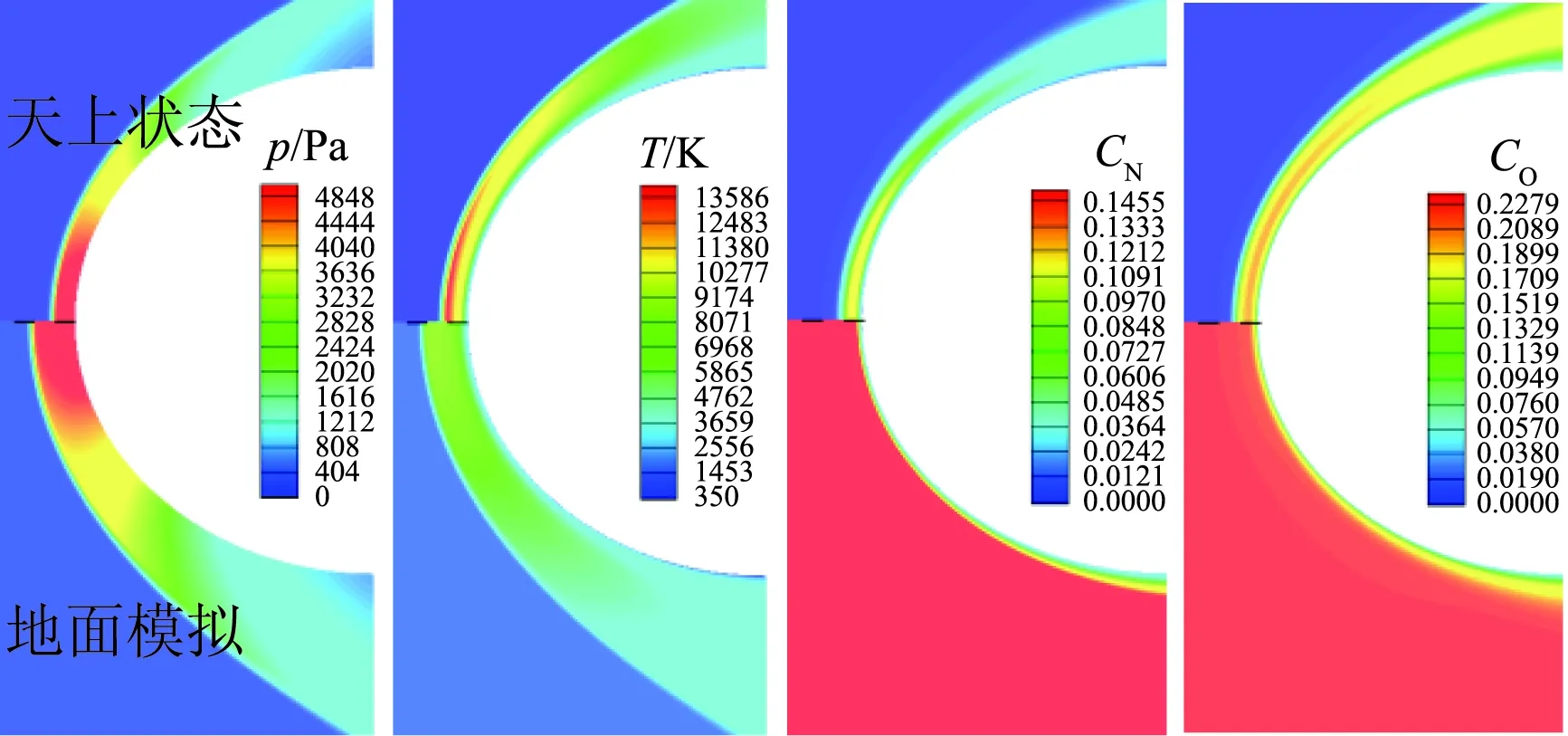
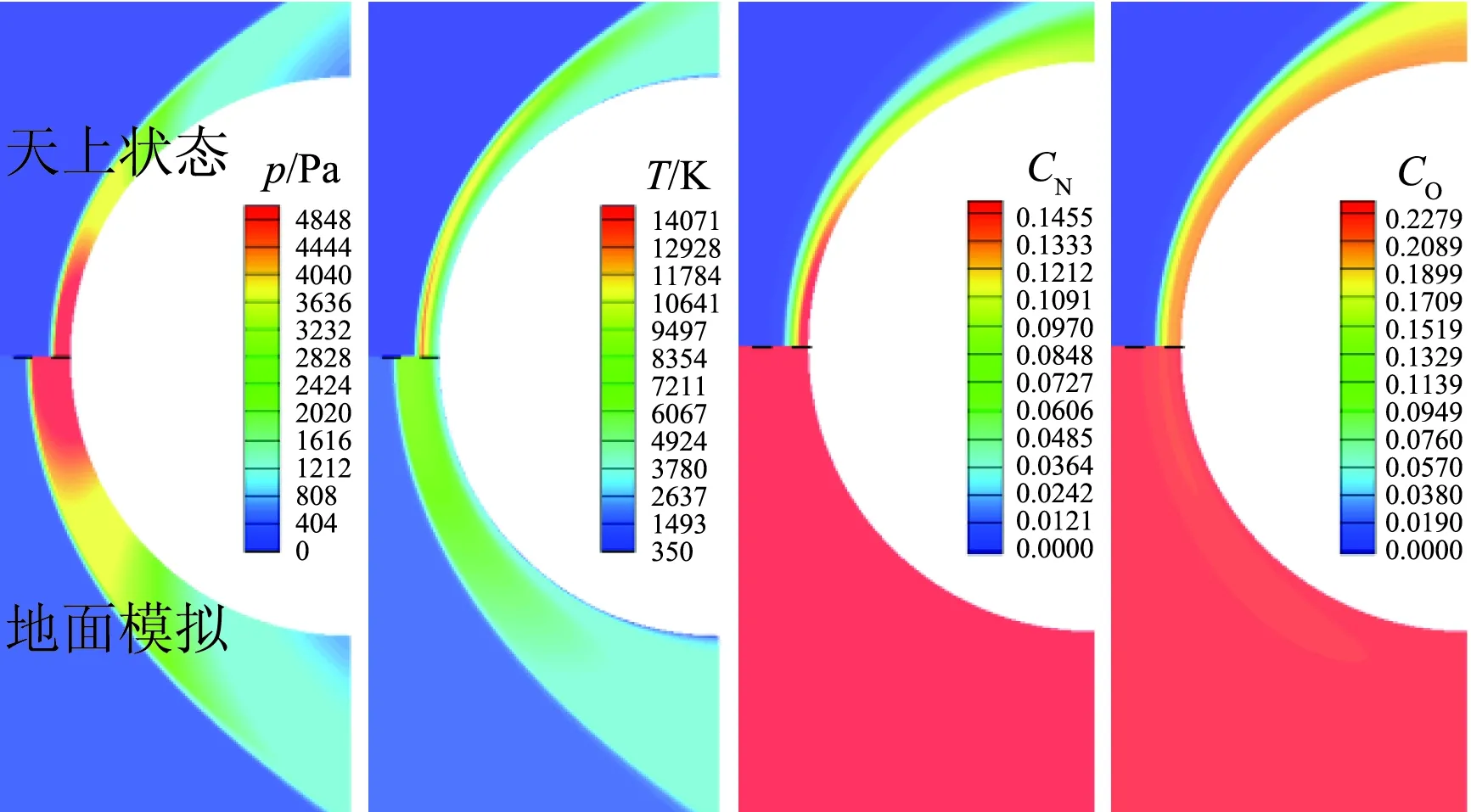
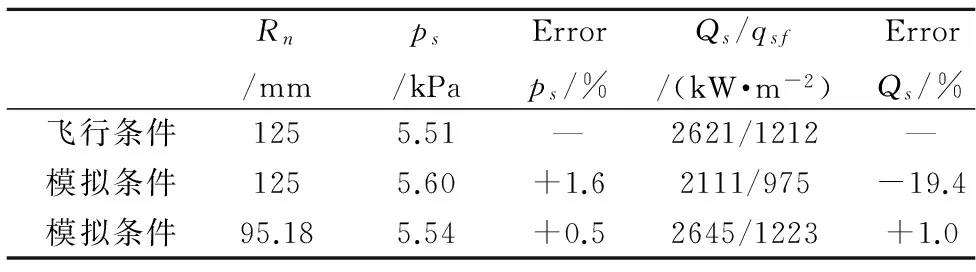
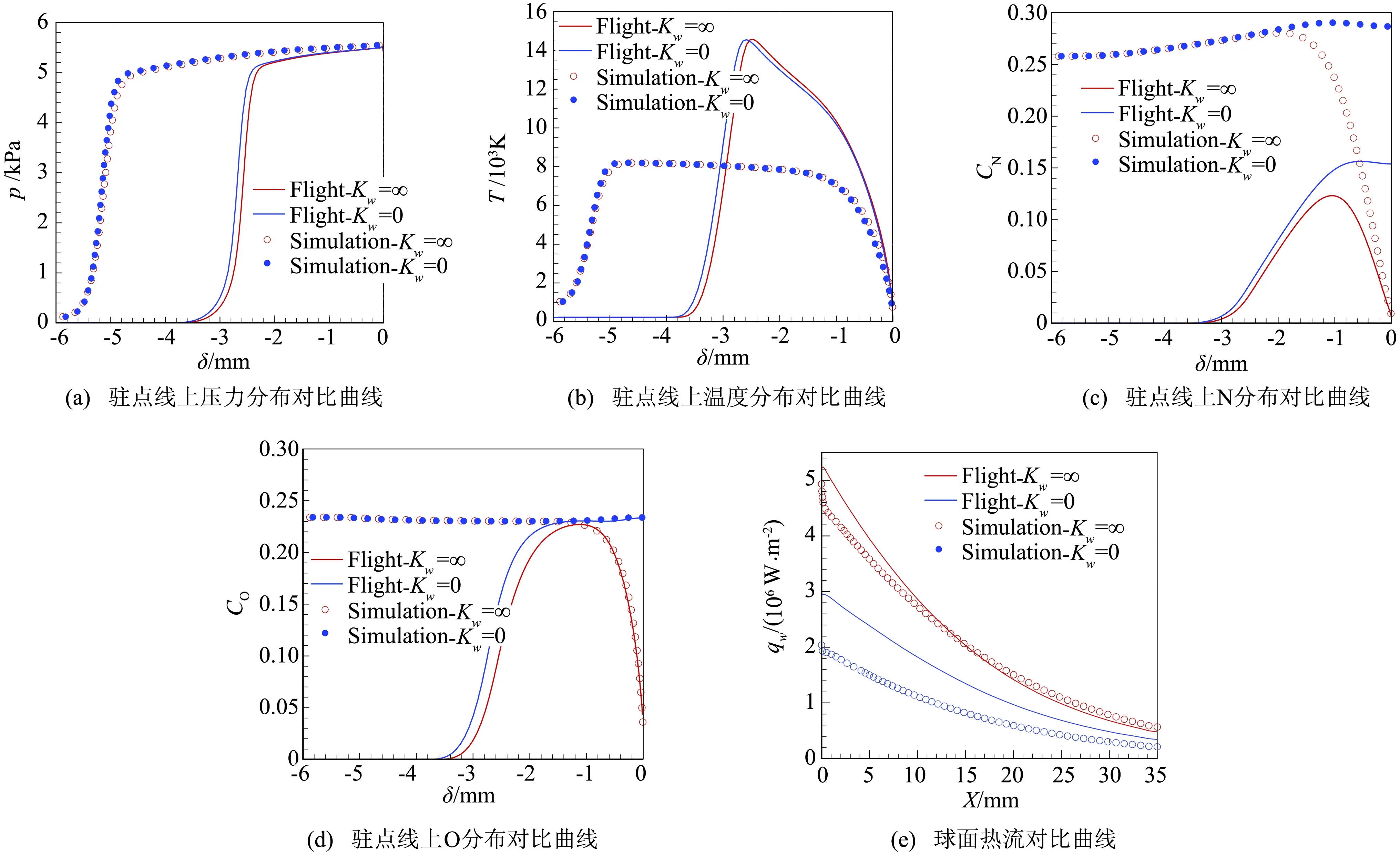
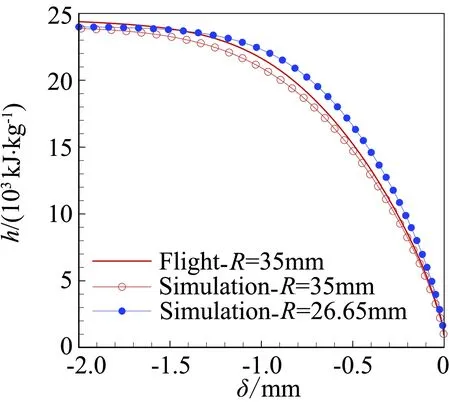
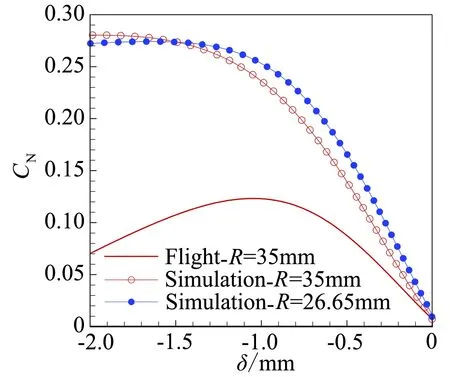
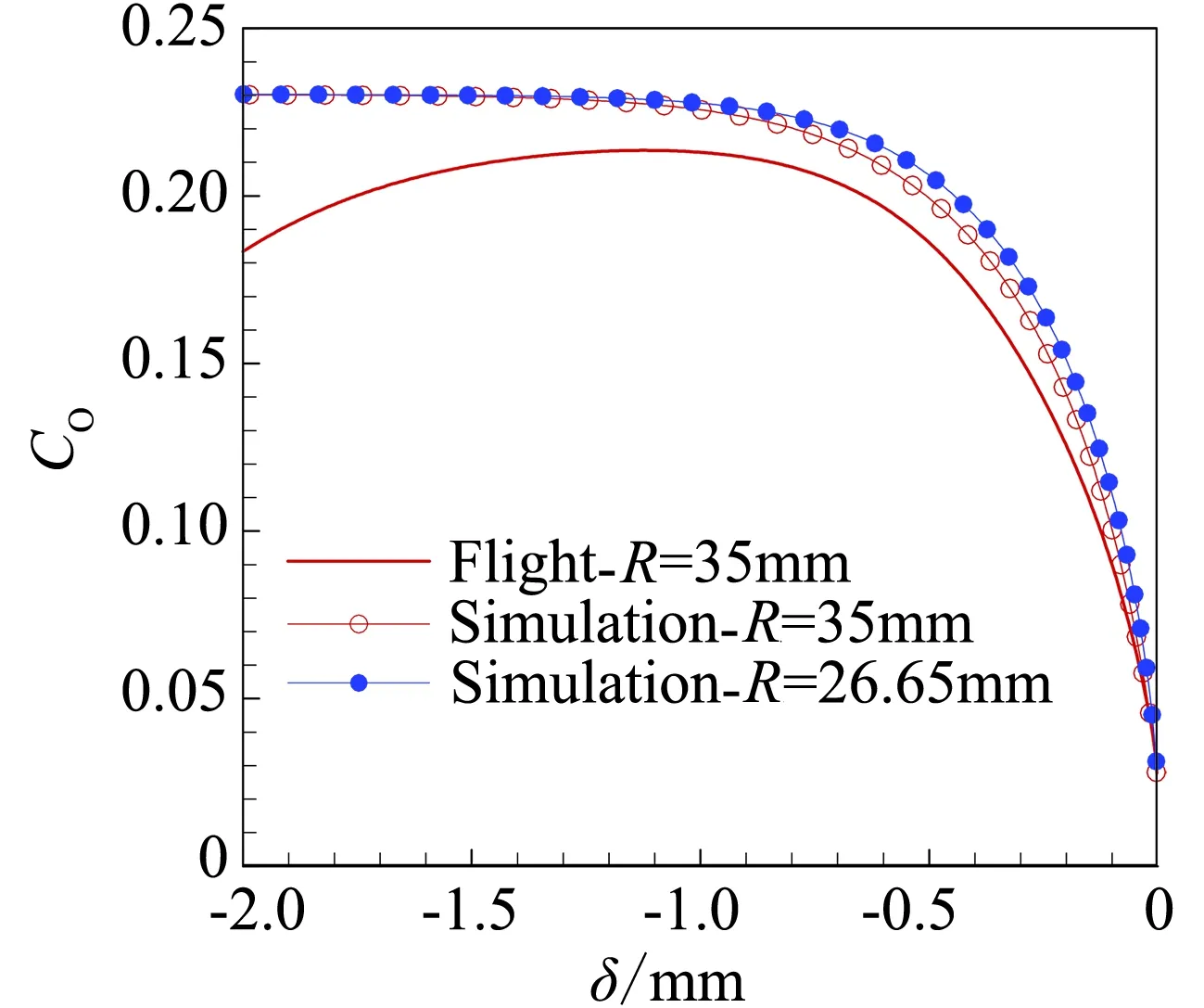
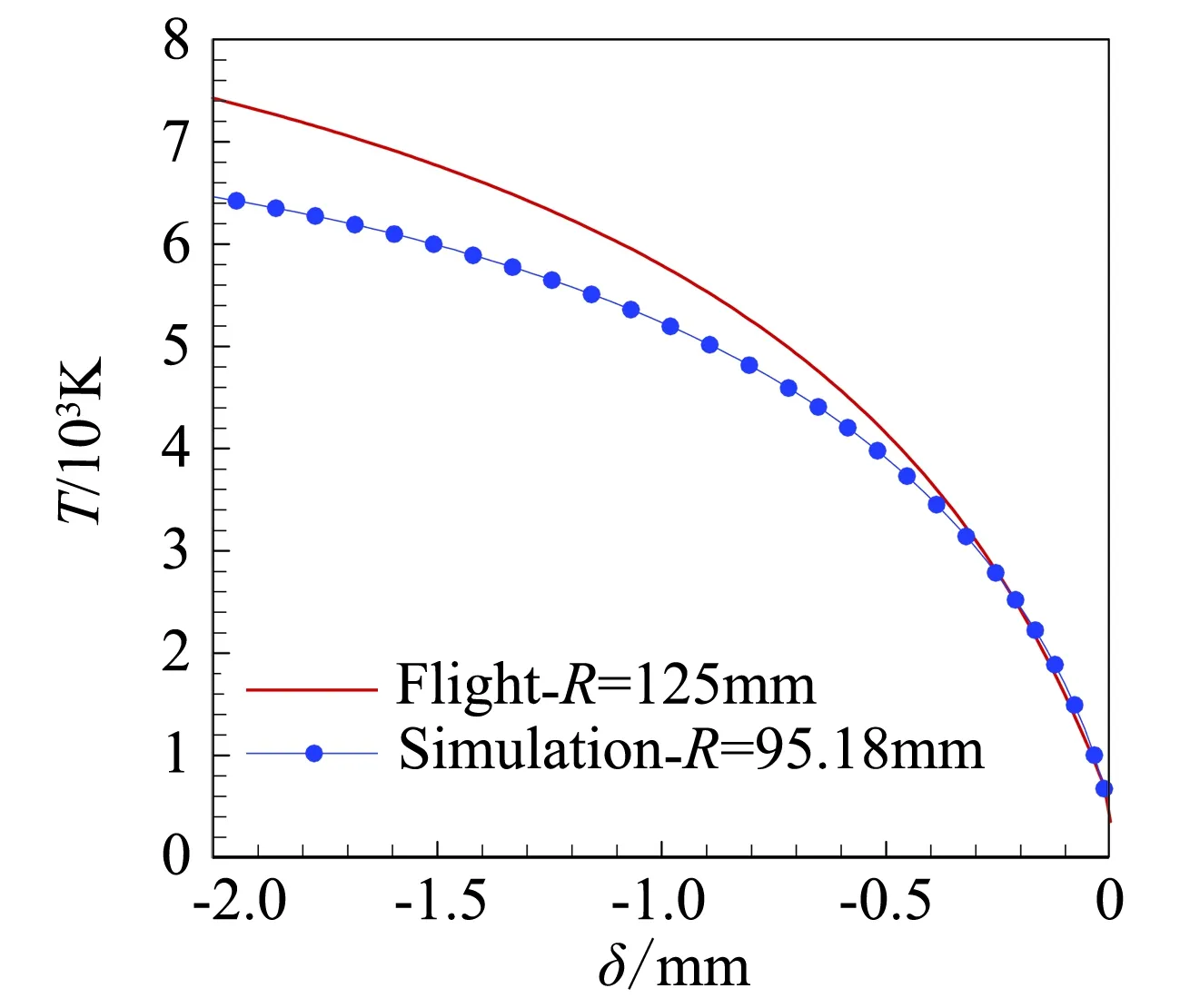
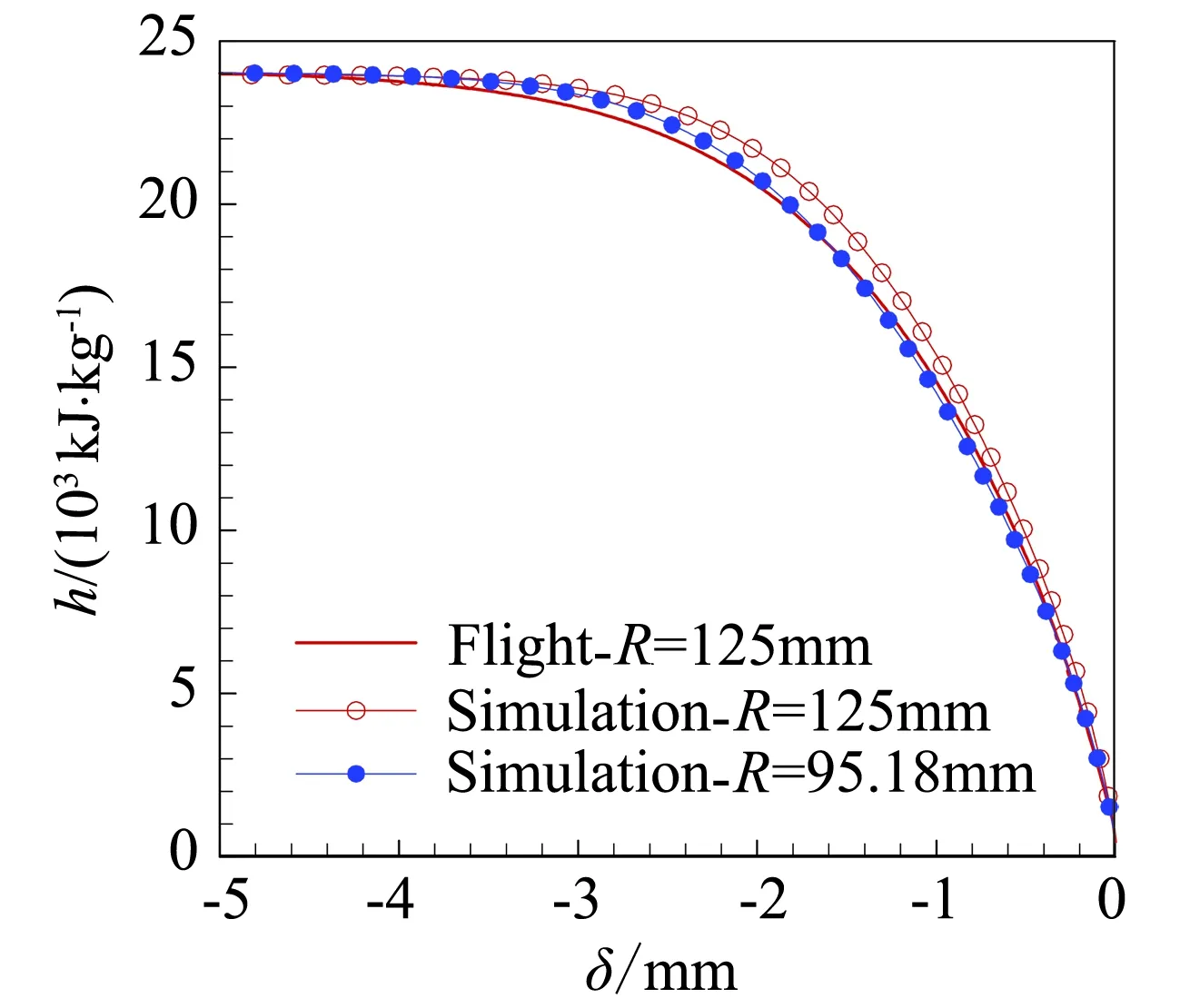
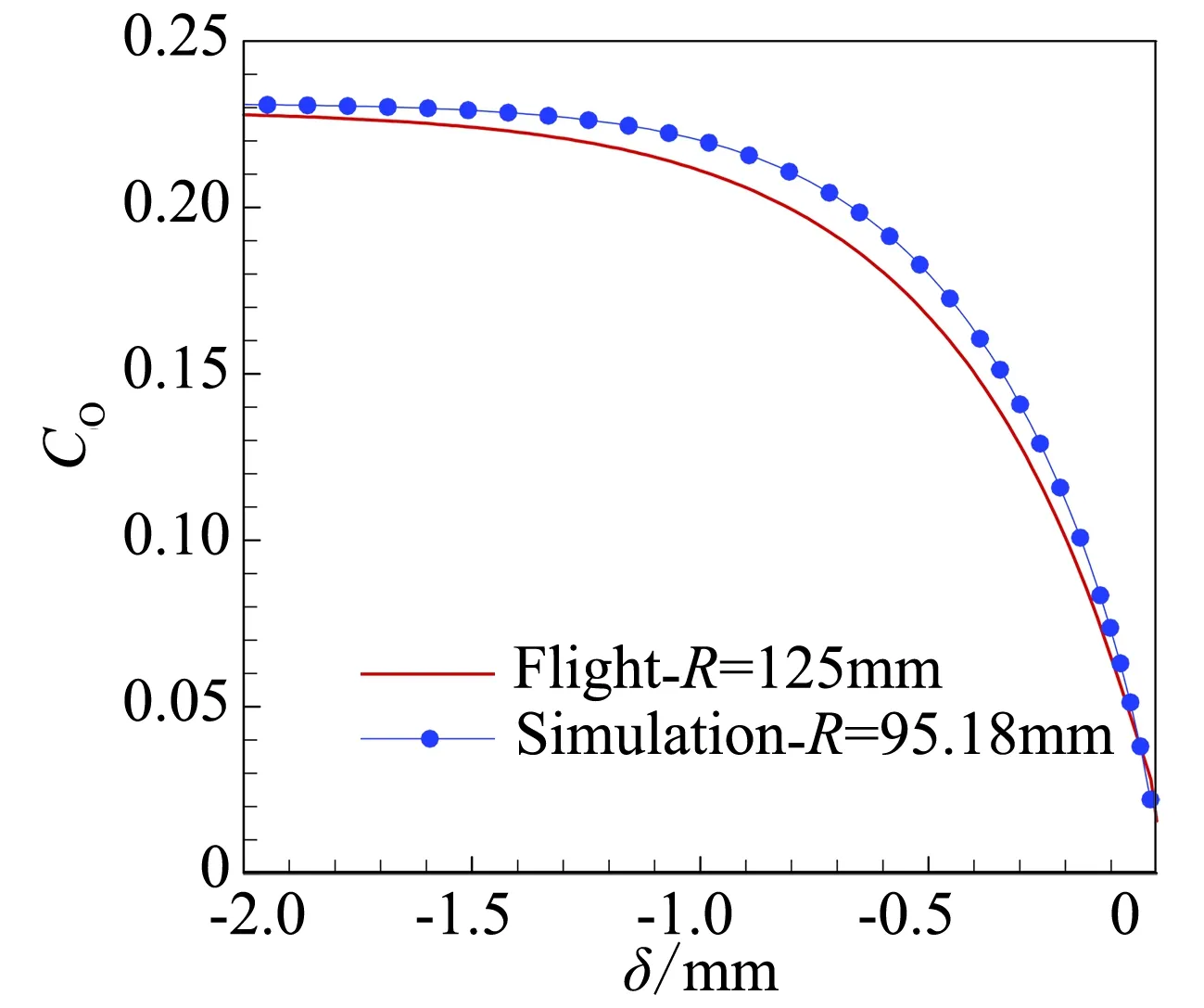
对于有限催化表面0 (10) 公式(10)表明:有限催化表面驻点热流大小直接受hD/ht和物面催化反应速率常数Kw的影响; 图1为驻点无量纲热流q/qf随hD/ht及表面反应达姆克勒数ρwKw/(α/Cp)s变化关系曲线。可以看出:当表面反应达姆克勒数大于100,q/qf趋向于1;当表面反应达姆克勒数小于100,q/qf随着表面反应达姆克勒数减小而减小,且不同hD/ht差异显著,表明:当物面接近完全催化特性时,离解焓对驻点热流不存在影响。 因此,对于平衡边界层和冻结边界层驻点,当物面接近完全催化特性时,流场的离解焓对驻点热流不存在影响,地面风洞条件模拟驻点化学反应流动加热的关键参数为总焓ht、驻点压力ps、驻点速度梯度βs。 天上状态总焓、驻点压力、驻点速度梯度分别由下式确定: (13) (14) 式(11)~式(14)中上标f表示飞行条件下的参数,下标s表示驻点条件。 地面风洞条件下,射流总能量由气体动能、内能以及离解能三部分组成,气流总焓通过如下关系式确定: (15) 超声速射流驻点压力依据如下关系式确定: (16) 超声速驻点区域速度梯度依据如下关系式确定: (17) 激波前后的密度比εs如下关系式确定式确定: (18) (19) 式(15)~式(19)中上标s表示风洞条件下的参数,下标s表示驻点条件。 (20) 根据上式,得到地面模拟环境下试样的有效尺寸为: (21) 因此,在地面试验中应该首先根据天上飞行状态下的总焓和驻点压力来确定风洞运行参数,进而根据公式(21)确定地面试验模型的尺寸,这样就能真实复现天上状态下头部驻点的气动热载荷。 采用数值求解非平衡Navier-Stokes方程,空气化学反应用5组分17个化学反应DunnKang空气化学模型的方法[15]验证上述模拟方法。 根据该飞行条件下的总焓和头部驻点压力确定了风洞的运行参数,得到的喷管出口流场参数见表1。 采用公式(21)可得到地面能够模拟Rf=35 mm、125 mm的模型尺寸分别为Rs=26.65 mm、95.18 mm。 图2、图3分别给出了不同催化特性条件下天上和地面风洞来流状态下半径R=35 mm球头绕流流场及驻点线参数,地面风洞来流O2基本完全离解,N2部分离解,来流体现出很强的非平衡特性,与天上相比地面驻点区流场有如下特点:1) 天上来流和地面风洞来流的组元差异较大;2) 地面风洞来流会使得头激波脱体距离有所增大;3) 头激波后流场压力差异很小;4) 材料的催化特性对壁面附近流场中的N、O组元影响较大,完全催化壁条件下整个球面热流与天上状态差异较小,完全非催化壁条件下驻点区热流差异较大,在远离驻点的区域差异逐渐减小。 表1 地面模拟流场参数Table 1 Ground test condition (a) 完全催化壁面 (b) 完全非催化壁面 不同半径球头驻点完全催化壁驻点热流和压力数值模拟结果对比见表2、表3,表中ps、Qs、qsf分别为驻点压力、驻点热流、驻点扩散热流。结果对比表明:1) 地面风洞来流条件下如果采用和飞行条件下飞行器相同的头部半径模型,尽管风洞条件能够模拟飞行条件下真实飞行器头部的驻点压力和总焓,但由于风洞模拟流场的绝对速度远小于飞行速度,导致风洞模拟试验中的驻点热流较飞行条件下的值偏小,当飞行器头部半径从35 mm增大到125 mm,这种模拟方法带来的偏差会增大;2) 依据公式(21)确定的飞行器头部半径35 mm和125 mm对应的风洞试验模型半径为26.65mm、95.18 mm,试验模型的驻点热流与飞行条件下的驻点热流相一致,偏差小于2%。 表2 驻点热流和压力的结果对比(R=35 mm)Table 2 Comparison of stagnation heat flux andpressure results (R=35 mm) 表3 驻点热流和压力的结果对比(R=125 mm)Table 3 Comparison of stagnation heat flux andpressure results (R=125 mm) 图3 不同催化壁面条件驻点线参数对比(R=35 mm)Fig.3 Stagnation line parameters comparison of different catalytic conditions(R=35 mm) 从图4驻点线近壁面流场变化可以看出:当飞行器的头部半径为R=35 mm时,风洞模拟也使用半径为35 mm的试验模型,虽然物面附近驻点线上CN的梯度略高于飞行条件的值,但CO的梯度小于飞行条件下的值,使驻点的扩散热流(2420 kW/m2)高于飞行条件下的值(1909 kW/m2);但是驻点线上温度分布在物面附近的梯度小于飞行条件下的值,驻点的传导热流(2296 kW/m2)小于飞行条件下的值(3299 kW/m2),最终两种热流的综合,导致风洞模拟条件下的驻点热流小于飞行条件的驻点热流。 当使用依据公式(21)的模拟准则确定模型半径为26.65mm,虽然驻点线上的温度分布在物面附近的梯度仍然小于飞行条件下的值,但驻点上的传导热流有所升高,达到2806 kW/m2;另外驻点线上的离解组元CN在物面附近的梯度升高,使驻点的扩散热流升高,达到2494 kW/m2,高于飞行条件下的值(1909 kW/m2),最终两种热流的综合,使风洞模拟条件下驻点热流略高于飞行环境的驻点热流。 飞行器的头部半径增大为125 mm时,风洞模拟使用公式(21)确定的半径为95.18 mm的模型,图5给出了飞行条件和风洞条件下头部流场参数对比,可以看出:驻点线上物面附近的温度分布梯度、CN和CO浓度分布梯度与飞行条件下的分布基本一致,驻点扩散热流接近(飞行条件:1212 kW/m2;风洞条件:1223 kW/m2)。表明:当飞行器头部半径较大时,依据公式(21)的模拟准则开展地面风洞试验,不仅能够模拟头部驻点的压力、热流、焓值,而且风洞试验模型头部物面附近的流场参数(温度、N、O组元的梯度)与天上飞行状态下飞行器头部流场的参数会趋于一致。 (a) 驻点线上温度分布对比曲线 (b) 驻点线上焓值分布对比曲线 (c) 驻点线上N分布对比曲线 (d) 驻点线上O分布对比曲线 (a) 驻点线上温度分布对比曲线 (b) 驻点线上焓值分布对比曲线 (c) 驻点线上N分布对比曲线 (d) 驻点线上O分布对比曲线 本文从平衡边界层和冻结边界层驻点气动加热公式出发分析了离解焓对不同催化特性驻点加热的影响,分析了地面风洞非平衡来流条件下头激波后流场参数的变化规律及与天上飞行状态的差异,建立了地面高焓风洞模拟完全催化壁驻点气动加热的模拟准则,可以得到的结论如下: 1) 在换热系数、总焓相同的条件下,离解焓对完全催化表面驻点热流不存在影响。 2) 地面风洞来流体现出很强的非平衡特性,无法完全复现头部的绕流流场;风洞条件下,激波的脱体距离会增大,试验模型材料的催化特性会对壁面附近流场中的N、O组元产生较大影响,完全催化壁条件下整个球面热流与天上状态差异较小,完全非催化壁条件下驻点区热流差异较大,在远离驻点的区域差异逐渐减小。 3) 对于完全催化壁驻点,地面风洞只要能够创造出与天上状态相同的驻点压力、驻点速度梯度和来流总焓,则能够复现天上飞行条件下驻点的气动加热。 4) 完全催化壁驻点,地面风洞试验如果采用飞行器头部半径相同尺寸的模型,驻点的热流会偏低于天上状态;而根据本文建立的三参数模拟准则确定的模型尺寸能够同时复现天上飞行状态下驻点区的焓、压力、热流,而且当飞行器头部半径较大时,驻点线近壁面的温度、N、O组元的梯度与天上会趋于一致。 参考文献: [1]Ou Yang Shuiwu.High temperature non-equilibrium air flow[M].Beijing: National Defence Industry Press, 2001.(in Chinese)欧阳水吾.高温非平衡空气绕流[M].北京: 国防工业出版社, 2001. [2]Anderson J D.Hypersonic and high temperature gas dynamics[M].New York: McGraw-Hill Book Co, 1989. [3]Gupta Roop N.Assessment of thermochemical nonequilibrium and slip effects for Orbital Reentry Experiment[C]//AIAA, Thermophysics Conference, 31st, New Orleans, LA, June 17-20, 1996. [4]Rosner D E.Non-equilibrium stagnation region aerodynamic heating of hypersonic glide vehicles[C]//Thermophysics and Heat Transfer Conference, Boston, Mass; United States; 15-17 July 1974. [5]Miao Wenbo, Cheng Xiaoli, Ai Bangcheng, et al.Surface catalysis recombination aero heating characteristics of hypersonic flow[J].Journal of Astronautics, 2013, 34(3): 442-446.(in Chinese)苗文博, 程晓丽, 艾邦成, 等.高超声速流动壁面催化复合气动加热特性来流条件对热流组分扩散项影响效应分[J].宇航学报, 2013, (03): 442-446. [6]Itoh K, Ueda S, Komuro T, et al.Hypervelocity aerodynamic and propulsion research using a high enthalpy shock tunnel HIEST[R].AIAA-99-4960, 1999. [7]Zeng Ming, Lin Zhenbin, Feng Hai, et al.Numerical analysis of non-equilibrium scale effects in hypersonic nozzle[J].Journal of Propulsion Technology, 2005, 26(1): 38-41.(in Chinese)曾明, 林贞彬, 冯海, 等.高超声速喷管非平衡尺度效应的数值分析[J].推进技术, 2005, 26(1): 38-41. [8]Lin Lie, Wu bin, Wu Chengen.Studies on surface catalytic effect of materials in a high-temperature gas flow[J].Acta Aerodynamica Sinica, 2001, (04).(in Chinese)林烈, 吴彬, 吴承康.高温气流中材料表面催化特性研究[J].空气动力学学报, 2001, (04) [9]Wang Guolin, Qu Yang, Chen Dejiang.Research on hypersonic vehicle thermal protection system of surface catalytic materials characteristics effect on aerodynamic heating[R].Mianyang: China Aerodynamics Research and Development Center, 2006.(in Chinese)王国林, 曲杨, 陈德江.防热材料表面催化特性对气动加热影响的研究[R].绵阳: 中国空气动力研究与发展中心, 2006. [10] Wang Guoxiong.Warhead technology[M].Beijing: China Aerospace Publishing House, 2009.(in Chinese)王国雄.弹头技术(上)[M].北京: 中国宇航出版社, 2009. [11]Gao Bing, Hang Jian, et al.The experiment exploration of catalyst effects on aerodynamic heat in real gas effects[J].Acta Aerodynamica Sinica, 2004.(in Chinese)高冰, 杭建, 等.高温真实气体效应中催化效应对气动热影响的实验探索[J].空气动力学学报, 2004. [12]Fay J A, Riddell F R.Theory of stagnation point heat transfer in dissociated air[J].Journal of the Aero-space Sciences, 1958, 25(2): 73-85. [13]Goulard R.On catalytic recombination rates in hypersonic stagnation heat transfer[J].Jet Propulsion, 1958, 28(11): 733-745. [14]Wu Wangyi.Fluid mechanics (down)[M].Beijing: Press of Peking University, 2010.(in Chinese)吴望一.流体力学(下)[M].北京: 北京大学出版社, 2010. [15]Dong Weizhong, Le Jialing, Liu Weixiong.The determination of catalytic rate constant of surface materials of testing model in the shock tube[J].Acta Aerodynamica Sinica, 2000.(in Chinese)董维中, 乐嘉陵, 刘伟雄.驻点壁面催化速率常数确定的研究[J].空气动力学学报, 2000.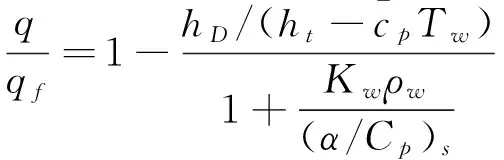
2 地面模拟参数的确定

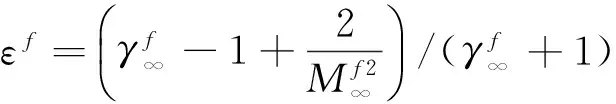
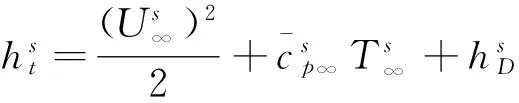
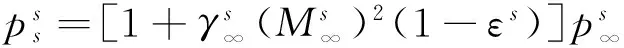

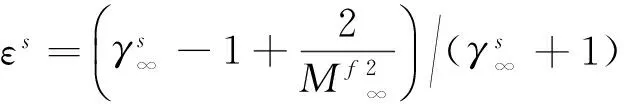
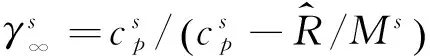


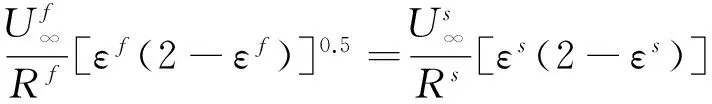
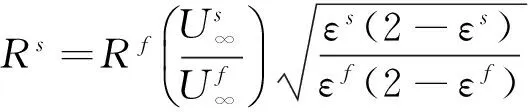
3 模拟方法验证
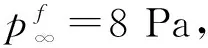




4 结 论
