用好“反客为主”方法 突破思维定式束缚

田加贵

(云南师范大学附属中学 650106)

思维的灵活性是指随机应变，触类旁通，不局限于某一方面，不受消极定势的束缚，它表现为多向思维和创造性思维.在中学数学学习中，思想方法纷繁多样，其中“反客为主”方法就是其中一种不失时机、灵活思变的多向思维和创造性思维方式.一些数学问题中的各“量”或各“元”之间的关系是辩证统一的，如果根据需要，将它们的地位适当变换，即“反客为主”，也称“反主为客”，常常使许多难题容易获解.

1 对于常量与变量进行的“主”“客”变换

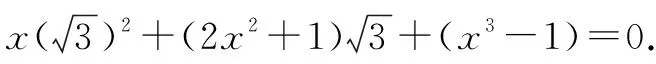
2 求解函数值域时进行的“主”“客”变换

图1

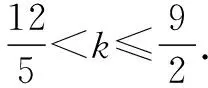
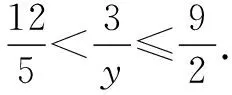
3 求解不等式时进行的“主”“客”变换

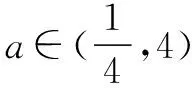
解析将关于x的一元二次不等式整理成关于a的一元一次不等式(x-1)a+x2-3x+1>0.

令f(a)=(x-1)a+x2-3x+1，

①当x=1时,f(a)=-1<0,不合题意.

4 求解函数中的参数时进行的“主”“客”变换

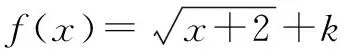
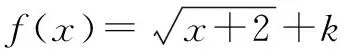
图2

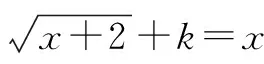
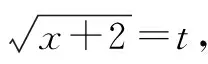
即y=t2-t-2(t≥0)与y=k有两个不同的交点.

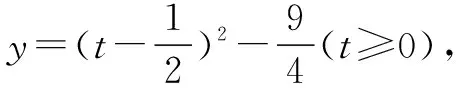
5 求函数的零点时进行的“主”“客”变换

例5设函数f(x)=ax4+x3+(5-8a)x2+6x-9a,其中a∈R,x∈R,无论a取何值时,都有f(k)=0恒成立,求k的值.

解析因为无论a取何值时,都有f(k)=0.即f(k)=ak4+k3+(5-8a)k2+6k-9a=0恒成立.

即(k4-8k2-9)a+k3+5k2+6k=0.

即(k+3)(k-3)(k2+1)a+k(k+2)(k+3)=0.

由于无论a取何值时,都有f(k)=0，

解得k=-3.

6 对于函数的定义域或值域中有参变数时的“主”“客”变换

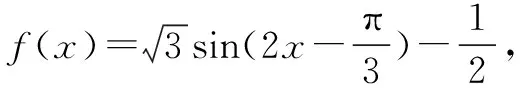
即-2≤f(x)≤1.

由于m-3≤f(x)≤m+3，

即fmax(x)-3≤m≤fmin(x)+3.

故1-3≤m≤-2+3.即-2≤m≤1.

故m∈[-2,1].

7 求直(曲)线族恒过定点时进行的“主”“客”变换

例7已知k∈R，若直线(2k+1)x+(k+2)y+2-2k=0恒过定点P，求点P的坐标.

解析将方程(2k+1)x+(k+2)y+2-2k=0化为(2x+y-2)k+x+2y+2=0.

因为无论k取何值时,点(2,-2)的坐标均满足方程(2x+y-2)k+x+2y+2=0，所以方程(2k+1)x+(k+2)y+2-2k=0表示过定点(2,-2)的直线方程.即点P的坐标为(2,-2).

8 对于直(曲)线方程中的系数与变量间的“主”“客”变换

例8已知两直线a1x+b1y+1=0和a2x+b2y+1=0的交点为P(2,3)，求过两点Q1(a1,b1),Q2(a2,b2)的直线方程.

解析由于点P(2,3)为两直线的交点，所以2a1+3b1+1=0，2a2+3b2+1=0.

对于直线2x+3y+1=0，显然两点Q1(a1,b1)，Q2(a2,b2)在该直线上，而两点确定一条直线，故过两点Q1(a1,b1),Q2(a2,b2)的直线方程为2x+3y+1=0.

9 求曲线方程时进行的“主”“客”变换

例9 已知方程4kx-4y-(4-k2)=0(k∈R)代表无数条直线，其中有且仅有1条过点A，则点A的集合记为M，设集合N={(x,y)|y=x-3}，求M∩N.

解析将原直线方程整理成关于k的一元二次方程k2+4xk-4(y+1)=0.由于有且仅有1条直线过点A，则关于k的方程k2+4xk-4(y+1)=0有且只有一解.故Δ=16x2+16(y+1)=0，得y=-x2-1.

此即为集合M的图象函数，它是一条抛物线.

解得点E,F的坐标为(-2,-5)，(1,-2).

所以M∩N={(-2,-5),(1,-2)}.

10 对于存在多个参数需要分清主次的“主”“客”变换

例10 若4kx2-8tkx-k2-2k-1≤0(k>0)对任意的t∈[-1,1]恒成立，求实数x的取值范围.

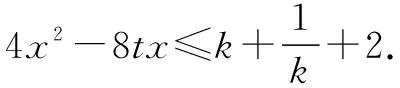
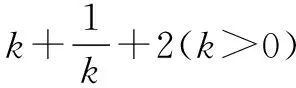
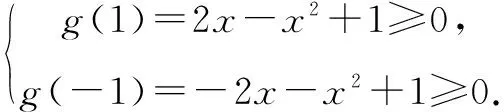
对于以上各种类型的问题，有些我们也可以不进行“主”“客”元变换，但也许解决起来可能麻烦一点，有些还真是不得不进行“主”“客”元变换，否则是无法解决的，“反客为主”自然也是“反主为客”，“主”与“客”之间本身也是相对的，只是对于某个元素来讲，它在题中的地位可能更突出一些，更应当得到重点关注，或者是说，各元在我们解答者的眼中，由于思维方法和观察角度的不同，“主”元与“客”元的地位突出程度也就不同，对于问题解答过程的影响程度当然也不同.这种方法既然具有多向思维和创造性思维的特质，所以有时使人觉得心旷神怡，耳目一新，但是要掌握好这种“主”“客”变换的方法有一定难度，我们只有在日常的学习中，多积累，多思考，才能更好地加以应用.