基于数字反向透热补偿的量子算法

王佳楠,丁泳程,郝敏佳,陈玺

(上海大学理学院,上海 200444)

2020年10月16日,习近平总书记在中共中央政治局第二十四次集体学习时强调,要充分推动量子科技发展,加强量子科技发展战略谋划和系统布局,把握大趋势.近年来,量子科技的发展具有重大科学意义和战略价值,是一项对传统技术体系产生冲击、进行重构的颠覆性技术创新,将引领新一轮科技革命和产业变革.量子计算被认为是未来具有重大影响力的新型计算模式之一.与传统计算机不同,量子计算机遵循量子力学规律,通过量子比特进行信息处理;基于微观量子比特的相干叠加和纠缠等特性以及量子电路的可逆性,在计算速度和能耗方面大大优于传统计算机[1].随着研究的不断发展,未来量子计算在人工智能、数据搜索、材料设计、生物制药等方面具有极大的潜在应用价值.2019年,谷歌推出名为Sycamore的量子处理器[2],集成53个量子比特,仅用200 s就能处理世界第一超算Summit计算一万年的实验,正式宣布实现了量子优越性.2020年,中国科学技术大学潘建伟团队成功构建了76个光子的量子计算原型机“九章”,这一突破使我国成为全球第2个实现量子优越性的国家[3].

众所周知,著名物理学家Feynman[4]于1982年首次提出量子模拟的概念.随后,Deutsch和Jozsa提出了Deutsch-Jozsa量子算法,展示了量子计算与经典计算的差异性[1].值得指出的是,1994年起Shor[5-6]提出了量子分解演算法——Shor算法,证明量子计算机在解决质因数分解问题上的速度远胜于经典计算机,使量子计算变成了热门的研究话题.1996年,Grover[7]发展了Grover量子搜索算法,在数据规模较大的情况下该算法的优越性十分惊人.近年来,人们还研究了许多有实际应用价值的量子算法,如量子行走、量子退火、量子玻色采样等,这些算法的研究在量子计算领域十分重要.尤其是对于量子退火[8],D-Wave于2011年宣布推出市场上第一款商用型量子计算机D-Wave One[9].运用量子绝热定理的量子退火技术并结合128个量子比特,可用于解决组合优化、旅行商等最优化问题.

目前,量子科技正处于含噪声中等规模量子时代[10],即从目前的硬件条件来看,在短时间内实现容错对于通用量子计算机来说是非常困难的.为此,Cerezo等[11]提出了变分量子算法,适用于含噪声中等规模量子器件的算法.这类算法是将经典算法与量子算法相结合,利用具有变分参数的量子电路,借助经典优化器最小化代价函数.实际上,最早提出的变分量子算法是变分量子本征求解器(variational quantum eigensolver,VQE)[12-16],该算法不仅能保证量子态的相干性,其计算结果还能达到足够的精度,在量子化学、量子多体物理等领域具有广泛的应用前景.另外,变分量子算法也可以解决一些优化问题.2014年,Farhi等[17]在绝热量子算法的基础上发表了量子近似优化算法(quantum approximate optimization algorithm,QAOA),通过在已知的初始基态上交替作用演化算符来求解经典哈密顿量的基态.该算法常用来解决组合优化问题[18-23],最为典型的案例就是最大切割问题.虽然QAOA不能保证总能获得全局最优解,但是在含噪声中等规模量子时代可以解决大部分实际问题.总之,变分量子算法结合了量子计算和经典优化器的优势,具有较好的发展前景.当然,该算法也存在一些局限性,如量子线路的可表达性、可训练性以及局部优化问题等[24].

近年来,上海大学陈玺教授及其合作者[25-28]提出了利用量子绝热捷径技术加速绝热慢过程,成为了当前国内外量子调控研究的一个主要方法,并广泛应用于量子信息处理和量子计算等领域.随着理论和实践的不断发展,人们可以通过变分法[29-30]、局域反向透热补偿法[31-32]和Floquet控制[33-34]等设计出不同系统的量子绝热捷径,以达到快速且高保真的量子态制备或操控.这里,反向透热补偿法可以在多体自旋体系中实现量子退火的加速[35-38].受到美国Google公司数字绝热量子计算工作的启发[39],本工作提出了数字量子绝热捷径计算的概念[40],并将其应用于量子因子分解[19]、投资组合优化[20]、组合优化[21]等方面.由此可见,量子绝热捷径中的数字反向透热补偿在量子绝热算法中起到了催化作用[41],同时数字反向透热补偿项能提供更多拟设,加速基态收敛,提高相关变分量子算法的性能.该方法被浙江大学尹艺和中科大郭国平课题组用于量子化学中电子态能量的计算[42].合肥本源量子计算科技有限公司也关注到了此方面的工作,将量子绝热捷径应用于QAOA中的解决组合优化问题[19].因此,基于数字反向透热补偿的量子算法及其应用成为量子计算的研究热点[43-44].

本工作以氢原子基态能量计算为例,首先通过反向透热补偿法设计绝热捷径,加速绝热量子计算;其次,结合VQE对反向透热补偿项进行优化,提高量子算法性能.研究结果表明,绝热捷径能够有效加速系统的演化时间,并且利用较少的迭代次数得到较高精确度.可见,基于数字反向透热补偿的量子算法在量子化学中具有重要的应用前景.

1 模型与哈密顿量

本工作首先考虑一般的分子哈密顿量,即包含如下部分:①每对核的核-核相互作用;②每个电子和每个原子核的电子-核引力;③每个核的动能;④每个电子的动能;⑤电子间的相互作用.图1为一个分子坐标系,图中分子内部存在相互作用[45].如果一个分子有N个电子和M个原子,以原子单位表示的哈密顿量为

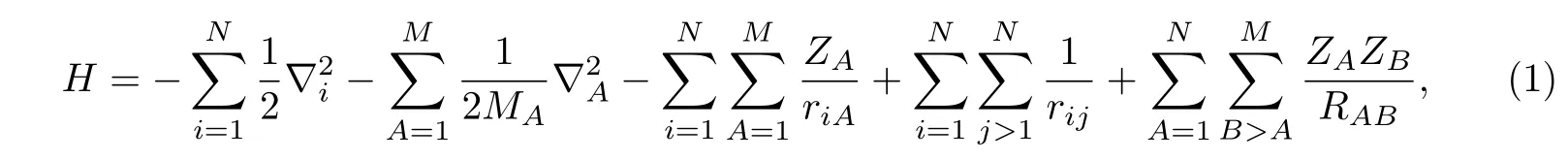
式中:A、B点为原子核;ZA为A的原子序数;MA为A的质量;i、j表示为电子.

由于原子核质量远大于电子质量,故原子核与电子相比移动速度很慢,可以通过玻恩-奥本海默近似来忽略原子核的动能.因此,将电子视作在固定核的场中运动,也就是说原子核之间的距离是恒定的.此外,电子波函数与核波函数是独立的,可以把总的波函数写成二者的直积:这里忽略核项,可将式(1)的电子哈密顿量写成这部分也即氢气分子的电子哈密顿量.

1.1 二次量子化

式(2)为一次量子化哈密顿量.将动量表象和位置表象变换到粒子数表象,并通过产生算符和湮灭算符ai来实现二次量子化,其中产生算法和湮灭算法满足反对易关系由此得到如下二次量子化的哈密顿量:

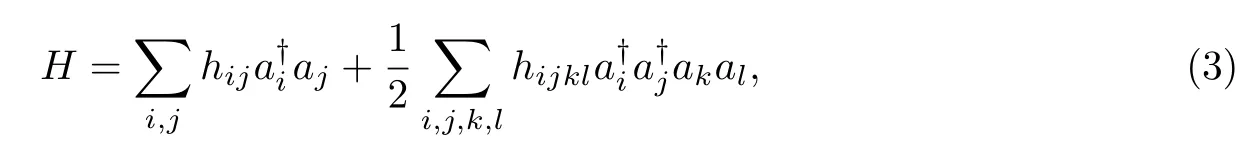
式中:hij、hijkl分别为依赖于核间距R的单电子积分和双电子积分,即

当χα(α=i,j,k,l)表示为不同单电子自旋轨道波函数,x1和x2表示为不同电子的位置时,具体hij、hijkl的积分可通过计算求得(见表1).

表1 核间距为R=0.74×10−10 m时的单电子积分和双电子积分Table 1 One-and two-electron integrals when internuclear distance R=0.74×10−10 m

1.2 Bravyi-Kitaev变换

为了数字模拟氢分子,通常需要把哈密顿量映射成量子比特的形式,并利用量子比特来表示费米子的自由度[46-47].常见的方法有Jordan-Wigner(JW)变换[48]和Bravyi-Kitaev(BK)变换[49-50],其中JW变换的优点在于简单,但变换前后所需量子比特数不变,不利于后续研究.因此,本工作在量子计算实例中采用BK变换以减少量子比特数.

在介绍BK变换之前需要定义一些量子比特集,这些量子比特集包含了将费米子算符应用于量子态所需的信息(fi表示第i个自旋轨道).

(1)更新集U(i).包含除i以外的量子比特,当轨道i的占有数fi改变时,这些量子比特必须更新.

(2)宇称集P(i).存储指数小于i的所有轨道宇称的量子比特,

(3)翻转集F(i).宇称集的子集,确定量子比特i是否与轨道i具有相同宇称.

(4)余子集R(i).宇称集的子集,也是翻转集的补集,R(i)=P(i)F(i).

对于轨道指数是奇数还是偶数,BK基的映射是非常不同的,因此需要区分这2种情况:

式中:Γj(Γ=X,Y,Z)表示将Pauli-Γ算符作用在第j个量子比特上.从而得到对应的哈密顿量为

这里,量子位1和3上只作用了Z门,故仅产生相位变化.根据这一特点,可将哈密顿量减少到2个量子比特.与此同时,可以再利用简化对应于量子位1和3的门.当假设BK基中的初态为时,量子位1、3都处于|0〉态,其关于Z门的本征值为+1,因此用2个量子比特可将初态表示为.为了与后续模拟时的量子位对应,将下标0、2改为0、1,由此最终哈密顿量为

2 反向透热补偿及其数字化

2.1 反向透热补偿法

如上所述,反向透热补偿有助于加快量子绝热过程.从多年的研究可以看到,VQE或QAOA的目的是利用量子-经典混合算法这一框架,求解出问题哈密顿量在低能下的位形,这与量子绝热捷径通过一个物理过程实现(末态)激发能量最小的原理是相通的.因此,下面将聚焦于数字反向透热补偿在量子算法中的应用研究,以期提升算法表现.为了由2个独立无相互作用的原子态H0制备一个氢分子基态Hf,可以根据绝热量子计算的思想,设计出含时哈密顿量H(t)=H0+λ(t)(Hf−H0),其中λ(t)=sin2(πt/T)∈[0,1],T为演化时间.将H0和Hf代入上式,可得

式中:H0=g0Z0+g1Z1,且系数分别为g0=1.252 0,g1=0.475 0,g2=0.909 5,g3=−0.921 0,g4=0.572 5,g5=0.090 5.当演化时间T足够大时,根据量子绝热定理系统沿着其瞬时本征态演化[51]:

2.1.1 局域反向透热补偿

根据式(11),可以得到精确补偿项的计算方式[31-32]:

那么在Htot(t)=Had(t)+Hcd(t)的共同作用下,系统的量子态可以在有限时间T内演化到|φn(H)〉.换一种形式,Hcd(t)可以写为[31,35]

式中:h(t)为一个单自旋的外加磁场.进一步推广至N个量子比特,这类被称作局域的反向透热补偿将不再有效[40].更需要指出的是,Zhang等[42]中采用了单比特近似,但是在量子化学问题中随着分子核间距的增大,该近似方法同样也会失效.

2.1.2 近似反向透热补偿

Polkonikova等[30]指出了反向透热补偿与绝热规范势之间的联系,即Hcd(t)=,式中为绝热规范势.进一步由Floquet控制思想,可以将规范势近似写成

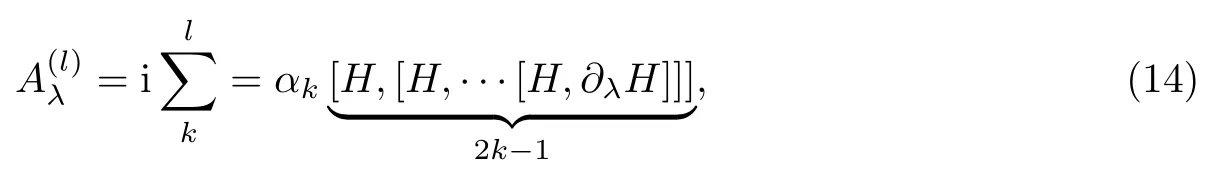
式中:系数{α1,α2,···,αl}可以通过最小化Sl得到,当l→∞时,为精确的规范势,为简单起见,这里取l=1,即为使S1最小时的系数.由上所述,哈密顿量所对应的近似Hcd(t)为

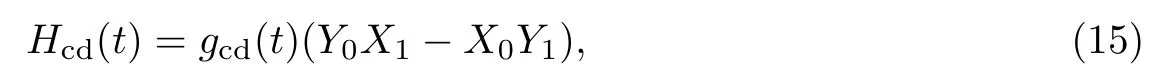
式中:系数gcd(t)为

因此,氢气分子的总哈密顿量Htot(t)为

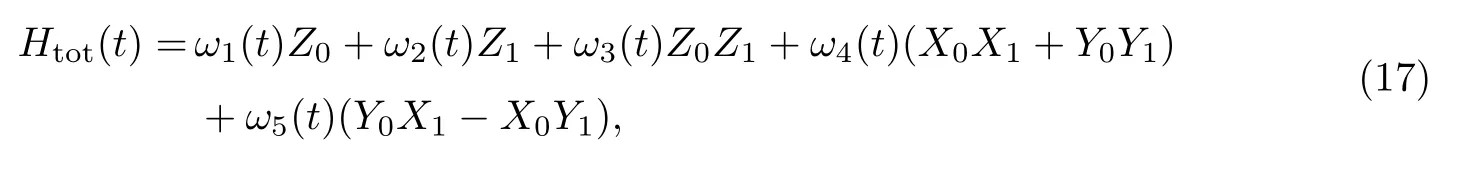
式中:ω1(t)=g0+λ(t)g2,ω2(t)=g1+λ(t)g3,ω3(t)=λ(t)g4,ω4(t)=λ(t)g5,ω5(t)=gcd(t).

2.2 数字量子模拟

利用一阶Trotter-Suzuki公式[52]:ei(A+B)t≈eiA∆teiB∆t+O(∆t2),∆t=T/n,可将Htot(t)对应的时间演化算符U(t)离散化为U≈UnUn−1···U1,其中Um=1,2,···,n=exp(−iHtot(m∆t)∆t).图2为数字化绝热捷径(digitized shortcuts to adiabaticity,STA)过程线路示意图.图中,以上述哈密顿量以量子门的形式添加到线路中进行数字模拟,其中初态为|01〉,即在|q0〉上应用一个X门,Un表示为每一步的演化算符,步长为∆t.

图2 数字化绝热捷径过程线路示意图Fig.2 Schematic diagram of digitized shortcuts to adiabaticity

第m步的时间演化算符可以拆分为,其中参数满足系统的总演化时间T随着步数的增加而变长,以∆t=0.1为例进行分析,在图3(a)中绝热过程大约需要50步才能接近于基态.但是采用近似反向透热补偿只需20步就可收敛于基态,明显加快了演化过程,从而实现量子绝热捷径.在相同步数的情况下对∆t=0.2进行比较,表明2种过程的趋势与∆t=0.1是一致的(见图3(b)).

图3 比较绝热演化(虚线)及绝热捷径演化(实线)所得基态能量Fig.3 Comparison of ground state energies obtained from adiabatic evolution(dotted)and the STA(solid)

表2比较了绝热和绝热捷径这2个过程所需量子门数量.结合图3可以得出结论:绝热过程至少需要19×50个量子门,相比之下,绝热捷径虽然每一步都需要更多量子门,但其总数远远少于绝热过程,即绝热捷径不仅可以缩短系统的演化时间,还可以减少量子门数量.这一点在量子线路具有噪声时显得特别重要.

表2 绝热和绝热捷径2个过程所需的量子门数量Table 2 Numbers of quantum gates required for adiabatic and STA

为了更好地描述不同∆t的能量对比,定义精度

式中:E为系统对应的步数能量;Eexact为系统的精确基态能量.图4为∆t=0.1和∆t=0.2的能量精度,实线表示当∆t=0.1时的绝热与绝热捷径(红色表示绝热,蓝色表示绝热捷径),虚线表示当∆t=0.2时的绝热与绝热捷径.虽然这2个过程的趋势相同,但是当∆t=0.2时精度明显降低,说明∆t的选取对演化结果也会产生影响,可见需要选择合适的∆t.

图4 ∆t=0.1与∆t=0.2时的能量精度比较Fig.4 Comparison of energy accuracy between∆t=0.1 and∆t=0.2

3 变分线路的最优化

变分量子算法可用于复杂波函数建模,成为量子计算中最有前景的算法之一.VQE是最先被提出的变分量子算法,使用变分原理计算哈密顿量的基态能量,被认为是量子化学的核心.利用变分量子线路优化近似反向透热补偿,首先利用初态|01〉以及对Htot(t)的离散化得到对应的试验态,随后计算试验态的能量期望值.在这个过程中,将Htot(t)离散化得到的量子线路作为拟设,通过调节Hcd(t)中的系数gcd(t)对线路进行优化(见图5).这里主要采用梯度下降优化器来进行操作,该优化器通过以下规则来更新参数:

式中:η为优化步长参数(η=0.4).以n=4为例,设定系统演化总时长T=1,那么线路中的初始参数为gcd(m∆t),其中m=1,2,3.如图5(a)所示,横坐标为参数更新的次数,当更新21次后系统能量期望值的精度由10−3提高至10−5.图5(b)为优化前后的gcd(t),圆点表示参数值.实际上,可以设定收敛值C,这个值越小参数更新次数越多;当C为10−10时需要更新67次精度才能达到10−9.

图5 应用变分思想对补偿项进行优化(设定收敛值为C=10−6,需要更新21次,且优化后gcd(t)强度增大)Fig.5 Counter-diabatic term is optimized by using the variational idea(Setting C=10−6,the parameters need to be updated 21 times,and the strength of gcd(t)increases after optimization)

将图5(b)中优化前后的参数带入量子线路中,得到每一步量子态对应的能量精度.虽然绝热捷径的能量已经接近基态能量,但优化后精度明显提高,在n=4时精度达到10−5.与绝热捷径相比,优化后速度更快结果更精确.

图6 当T=1,n=4时,绝热捷径与优化后的能量精度对比Fig.6 Comparison of accuracy between STA and optimization when T=1,n=4

事实上,在计算近似补偿项时只取了1阶,但是在计算2阶时发现0,也就是说式(16)是个精确解.当考虑大分子时,需要更多的量子比特以及多体相互作用,同时需要引入2阶甚至更高阶反向透热补偿项,这在后续工作中值得进一步优化以及考虑量子线路的实现.

另外,由于在模拟过程中采用了Trotter-Suzuki展开,并忽略了O(∆t2),故引入优化的反向透热补偿项能有效抑制Trotter误差.然而随着更高阶的引入,虽然可以提高精度,但是每个步骤则需要更多的门或实现多体相互作用,这使得量子线路的复杂度增大.因此,后续研究量子门数目、线路复杂度、绝热误差、Trotter误差之间的关系成为重要课题.

4 总结

本工作以量子化学为例介绍了基于数字反向透热的量子算法以及优化等.为了详细介绍相关领域的背景和进展,首先构造了氢气分子的哈密顿量并对其进行变换,利用产生算符和湮灭算符,将动量与相对位置表象变换到离散化的粒子数表象,可以得到二次量子化的形式;再通过BK变换把哈密顿量从费米子算符转换为Pauli算符和的形式,以便在量子计算机上进行模拟.为了解决绝热演化时间过长的问题,首先利用反向透热补偿法,通过找到一个额外的哈密顿量作为补偿项来实现系统的快速绝热;然后将总哈密顿量通过Trotter-Suzuki展开进行数字量子模拟,以便在较少的步数内达到目标态且保持高保真度;最后借助VQE来优化补偿项,使结果更加精确且更新次数减少.

量子化学是量子计算中重要的应用之一.人们已经在光量子处理器上验证了变分法求解特征值[13],并通过量子化学计算了分子的基态能量.谷歌AI量子团队使用VQE实现了迄今为止最大规模的化学模拟计算[16],为量子算法的改进和应用提供了新方向.如何结合机器学习,将基于数字反向透热的量子算法用于计算大分子量子模拟[53]、激发态能谱计算,甚至量子材料的设计[54]等将是后续研究的重点,也是有望在这些应用中展现出在含噪声中等规模量子时代的量子优势.

最后,必须指出的是,本工作以量子化学为例展示了基于数字反向透热的量子算法的构建和应用.如上述所述,也可以将该算法应用于高能物理、蛋白质折叠等科学问题上.相信在上海大学新一轮“五五战略”量子科技发展的战略指引下,量子计算特别是数字反向透热的量子算法能做出具有特色的工作.