振动驱动热对流研究进展

郭茜里,吴建钊,王伯福,庄启亮,周全,刘宇陆

(上海大学力学与工程科学学院上海市应用数学和力学研究所,上海 200072)

几乎所有的机械装置都不可避免地受到振动激励的影响,尤其对诸如汽车、水下航行器、空间飞行器以及空间站等内部精密流体机械设备而言,振动激励产生的影响更是不可忽略.振动激励在自然界也很常见,如即使在没有重大地震发生时,地球也正经历着持续的振荡.研究发现,当具有温度梯度的流体受到振动激励时,流体内部会在振动热浮力作用下出现对流现象[1-3],这种由振动引起的对流流动被称为振动热对流.振动热对流可以像浮力驱动热对流一样输送物质和热量.在振动热对流中,振动激励主导着流动结构的生成演化过程,并决定着动量、能量和热量输运规律.当施加的振动为小振幅高频振动(振动周期远小于系统黏性耗散时间)时,流场可以分解为快变部分和慢变部分.快变部分为振动激励产生的振荡流动;而慢变部分为在振动周期时间平均后的流动,体现了流动对周期性激励的非线性响应[4].慢变流的存在有利于提供时间平均意义上的传热传质机制.特别是在微重力环境中,研究人员可以利用高频振动激励产生的平均流实现传热传质[5-6].因此,对振动驱动热对流的流动结构和传热特性进行深入的研究,可以帮助人们认识和理解振动热对流的传热传质机理,同时为工程应用提供重要的理论指导和突破性思路.

考虑一个简单的振动热对流模型,封闭的对流方腔(宽高比为Γ=L/H=1)内流体受到水平或竖直的温差,施加的振动激励为简谐振动Acos(Ωt)n(其中A为振幅,Ω为振动频率,n为振动激励的方向,L和H分别为对流腔体的水平宽度和高度).选择振动激励固连的坐标系为参考系,在考虑含重力的情况下,方腔内流体介质受到的合加速度为重力加速度与振动引起的附加牵连加速度之和,即−gz+AΩ2cos(Ωt)n(其中g为重力加速度大小,z为竖直方向的单位矢量).如果考虑微重力环境下的振动热对流模型,则流体介质受到的加速度仅为AΩ2cos(Ωt)n(见图1).由于振动热对流系统中流体的温度与速度耦合,故温度变化会引起密度的变化,密度变化进一步引起重力和附加惯性力对应的浮力变化.考虑系统温差∆很小的情况,引入Oberbeck-Boussinesq(OB)假设将问题简化,即流体的物性参数(如黏性系数ν、热扩散系数κ、热膨胀系数α等)均不随温度T而改变,而流体密度ρ近似认为是温度T的线性函数,即ρ(T)=ρ(T0)(1−α(T−T0)),其中T0为对流槽的平均温度.在OB假设下,振动驱动热对流系统的控制方程包括:

图1 微重力振动热对流系统物理模型示意图Fig.1 Sketch of physical model of thermal vibrational convection system in microgravity

(1)连续性方程:

(2)Navier-Stokes方程:

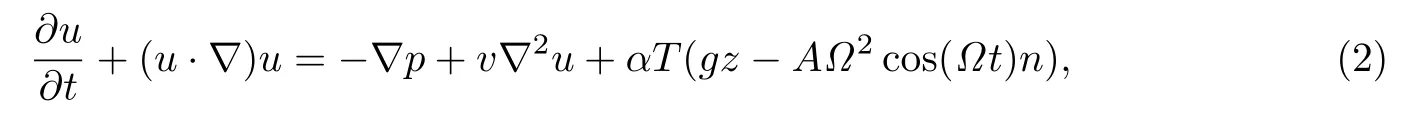
(3)热输运方程:

式中:t为时间;u为速度矢量;T为流体温度;p为压强与流体密度的比值.控制方程组(1)∼(3)分别为对流系统的质量、动量和能量守恒.振动热对流系统中存在4个无量纲控制参数:瑞利数Ra、普朗特数Pr、与振动激励相关的无量纲振幅a和振动频率ω:

式中:Ra数为热浮力驱动力与黏性力的比值,表征无量纲化的温差;Pr数为动量扩散速度和热扩散速度之比,描述流体本身的物理性质.对流腔体的几何特征用宽高比Γ来描述.此外,引入振动瑞利数Ravib描述平均振动效应[4]:

振动热对流系统的2个重要响应参数分别为努塞尔数Nu和雷诺数Re:

式中:J为对流腔体实际热通量;λ为流体的热传导系数;U为流动的特征速度.Nu数为J与热传导时热通量(λ∆/H)之间的比值,描述了系统的对流换热效率;Re数表征热对流的流动强度.对于不同的振动热对流物理模型,在给定了相应的温度和速度边界条件后,均可采用上述控制方程进行求解.

近年来,为了探究振动热对流的驱动机制,也为了满足未来航空航天应用发展的需求,在微重力环境下的振动驱动热对流的实验、数值和理论研究引起了许多研究人员的兴趣[7-10].在地表重力环境下,研究发现振动激励可以有效地改变热对流的流动结构生成演化过程,实现系统传热的控制.

1 微重力条件下振动热对流研究

在微重力环境下,飞行器的姿态调整、航天员的活动、发动机点火以及空间碎片撞击等会使空间环境的加速度出现微小跳动,这些跳动被称为重力跳动(g-jitter).由于恒定的重力跳动被认为是引起微重力质量和热量输运的可能因素,故研究人员开始重视和研究重力跳动引起传热传质的物理机制,振动热对流的相关研究应运而生.由于微重力环境中浮力作用几乎消失,在动量守恒方程(2)中重力引起的浮力项作用很小甚至可以忽略不计,因此重力跳动引起的振动浮力项起着主导作用.微重力振动驱动热对流系统的物理模型如图1所示,图中采用简谐振动表征恒定的重力跳动,规定垂直方向为平行于温度梯度方向,水平方向为垂直于温度梯度的方向.

微重力振动驱动热对流现象的发现最早可追溯到阿波罗17号的热对流实验,Grodzka等[11]对这些热对流现象进行了详细的讨论,并证实航天器设备的运行和宇航员的运动是引起重力跳动的主要因素,并且由重力跳动产生的传热效率超过了纯热传导的情况.可见,在微重力环境下,外部的振动激励是实现传热的一种有效手段.在较早期的研究中,不同的振动方向对流动稳定性的影响是主要的研究问题之一.Gershuni等[12]分析了在失重环境中,垂直振动激励下不同几何构型的线性稳定性;随后,Gershuni等[13]进一步对水平振动激励下发生的振动对流进行了数值研究,证明了在水平振动下系统无法维持稳定状态,并确定了在失重条件下振动热对流的流动结构.结果表明,当小于临界Ravib数时(=15 000),在对流方腔中出现四涡结构(见图2(a)),此时四涡结构处于稳定状态,其为反转的三涡结构的时间平均结果.随着Ravib数的增大,四涡结构处于亚稳态,随着时间演化最终会过渡到一个稳定的三涡结构(见图2(b)).而后,Hirata等[14]通过数值模拟进一步研究了在失重条件下垂直振动对流动状态的动力学响应,在较宽的频率和振幅范围内,观察到了流动对振动激励的同步、次谐波和非周期响应,并认为非周期响应这一特征可能与流动状态转变有关.由于在空间飞行器进行微重力实验的机会少而且费用高,Mialdun等[15]巧妙地设计了微重力振动热对流实验装置,利用飞机抛物实验首次在陆地上观察了微重力环境下的振动热对流现象,并验证了以往研究报道的瞬态下由四涡结构向三涡结构过渡的流动现象.在后续研究中,Shevtsova等[16]采用3维直接数值模拟和基于平均流控制方程的2维数值模拟得到的结果与Mialdun等[15]的实验结果吻合较好,发现随着振动强度的增大,振动产生的平均流动对传热有显著增强的作用.如图3所示,Nu数随Ravib数单调递增,说明振动激励越强传热效率越高.该研究还分析了在不同等级微重力情况下重力跳动对传热和流动分岔情况的影响[16].如图4所示,当流函数Ψ接近于0时,流动表现为四涡结构.一段时间后,Ψ偏离0,其绝对值开始增长,直到平均场达到稳态,Ψ的增长与向三涡结构的转变有关.在图4中,曲线1和2的变化也反映了重力对流动结构演化有一定的稳定作用(z方向为重力方向和温度梯度方向).重力的存在延迟了四涡结构向三涡结构转变的过程.曲线3和4表明,即使是很小的重力(gx=10−6,x方向垂直于温度梯度方向),也可以让四涡结构提前失稳至三涡结构,并且gx的方向控制了在稳定状态下三涡结构中对角涡的倾角和旋转方向[16].

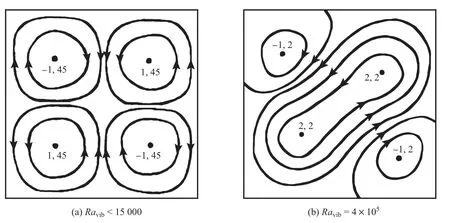
图2 微重力环境下振动热对流的流动结构Fig.2 Flow structure of thermal vibrational convection in microgravity

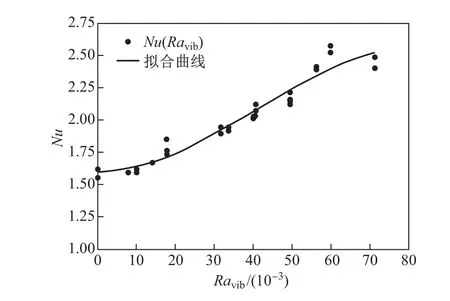
图3 微重力条件下Nu数随Ravib数的变化Fig.3 Plots of Nu numbers as a function of Ravib in microgravity

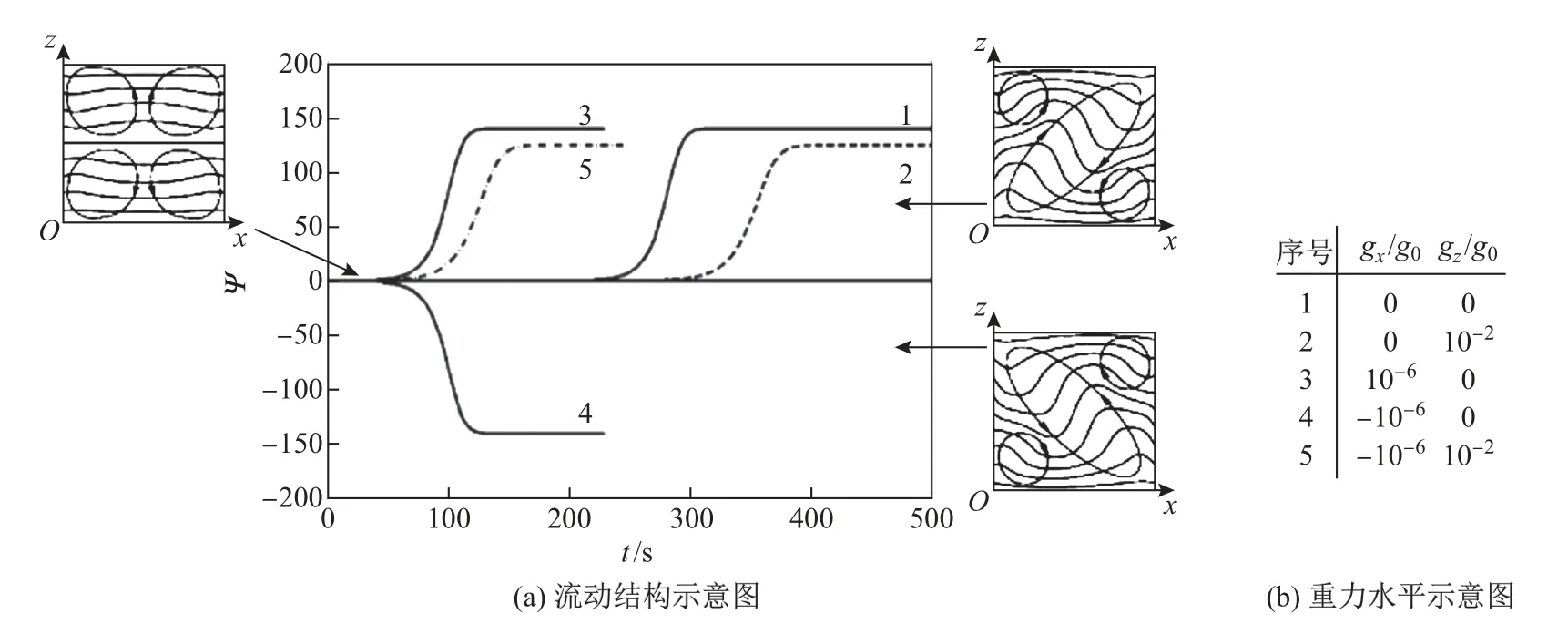
图4 Ravib=71.15×103时不同重力水平下的流函数值和相关流型的时间演化(显示了对应的流线和温度等值线)Fig.4 Evolution of the sum of stream function values for different levels of residual gravity and related flow patterns when Ravib=71.15×103

2 地表重力环境下振动热对流研究

在过去十多年中,研究人员分析了在重力环境下振动激励对不同热对流模型的流动结构和传热的影响.从振动Rayleigh-B´enard(RB)热对流[1,17-18]、振动侧壁热对流(vertical convection,VC)[3,19-22]以及振动水平热对流(horizontal convection,HC)[23]的研究可以发现:当振动方向与温度梯度方向垂直时,振动产生的剪切效应加速了温度边界层的失稳,促使生成大量羽流结构,显著增强系统的对流换热效率;反之,与温度梯度平行的振动激励可以有效地抑制羽流结构的生成,从而减弱对流强度并降低系统传热效率(见图5).

2.1 振动Rayleigh-B´enard热对流

振动RB热对流[24-26]是典型的热对流系统之一,可以简单描述为在一个充满流体介质的密闭容器中,下导板加热上导板冷却,在热浮力驱动力的作用下对流腔体底部的流体受热膨胀变轻而向上运动,对流腔体顶部的流体遇冷收缩变重而向下运动,从而形成大尺度环流输运热量.在RB系统研究领域中,如何有效提高封闭对流系统的热输运效率一直是人们关心的核心问题,为此研究人员提出了很多方法,如引入粗糙壁面可以改变边界层内流动结构生成演化特性,从而有效提高系统传热效率[27-31],或在某些参数范围内会抑制传热[32];通过几何约束使羽流合并可以实现增强传热[33-34];采用倾斜对流腔体和几何约束的组合能够在较低的Pr数和Ra数条件下使传热增强数倍[35-36].此外,施加外部振动激励可以破坏边界层稳定性,是实现控制传热的另一个重要手段.在现有研究中,国内外研究人员通过对RB系统施加振动以实现对系统稳定性、流动结构和系统传热的调制作用[1,17-18],其物理模型如图5(a)所示.

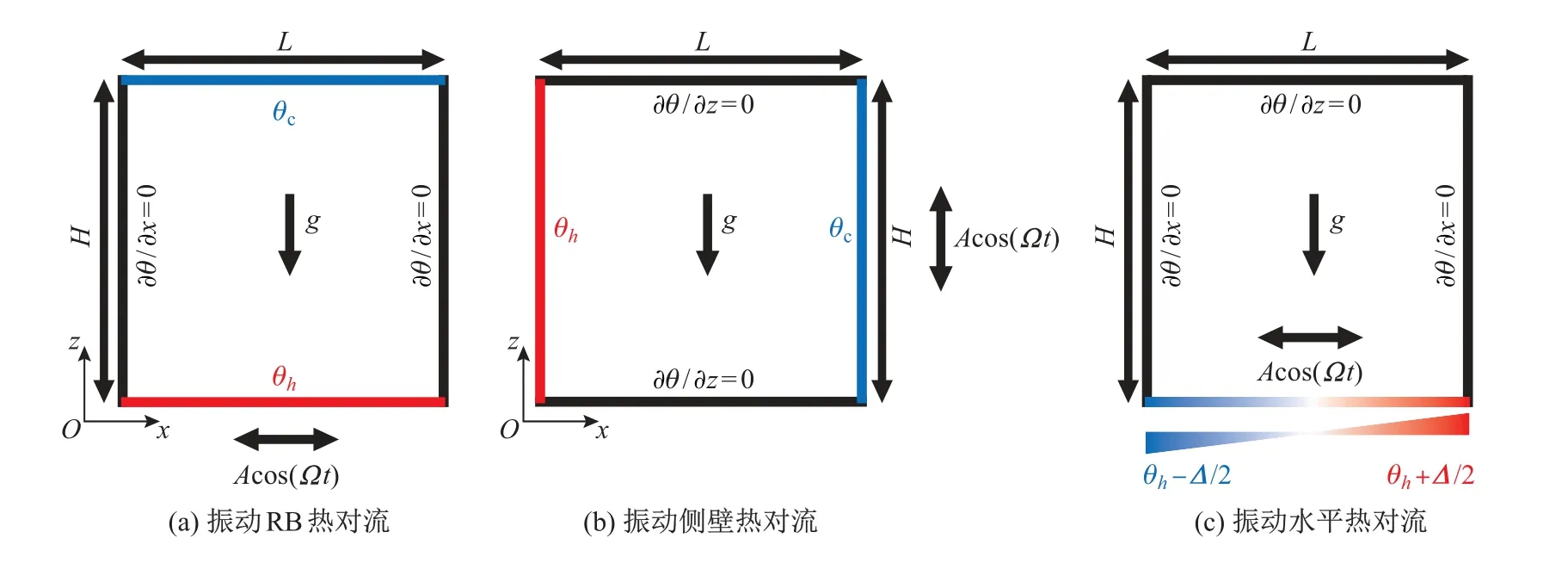
图5 地表重力环境下振动热对流系统物理模型示意图Fig.5 Sketch of physical model of thermal vibrational convection system under terrestrial conditions

在稳定性方面,Zen’kovskaya等[37]在含高频振动的Boussinesq方程中引入快变慢变分解方法,研究振动对热对流的影响;Gershuni等[17]分析了平均方程的线性稳定性,引入了振动瑞利数Ravib以定量刻画振动激励强度;Gresho等[18]研究了振动激励对从上或从下加热的水平流体层的稳定性的影响.线性稳定性分析结果表明,重力调制可以显著地影响系统的稳定性.对于正的Ra数(下导板加热,上导板冷却,温差为正),较大的数在高频和小振幅时稳定;对于负的Ra数(上导板加热,下导板冷却,温差为负),在任何振幅和频率的参数范围内都可以失稳,其中高频大振幅下最不稳定.此外,振动方向也是影响系统稳定性的关键因素.Ciss´e等[1]讨论了RB热对流中不同宽高比的对流腔体受振动强度和方向的影响.研究结果表明:高频垂直振荡可以延迟对流不稳定性,从而有效抑制对流流动,使系统能保持RB热对流阈值以上的热传导状态;而当振动方向不平行于温度梯度时,由于固壁的存在,水平方向的振动使系系统无法达到力学平衡,加速了温度梯度的不稳定,导致了平均流的产生.Wang等[2]进一步对水平振动的RB热对流进行深入的研究,其数值模拟结果发现,在湍流状态时振动热对流系统中的热输运得到了较大的增强,流动结构也发生了巨大的改变.如图6所示,当不施加振动ω=0时,热羽流沿着腔体侧壁向上运动,冷羽流向下运动,在腔体内形成了一个沿对角线方向的逆时针大尺度环流结构[2].当水平振动作用于对流腔体时,振动激励在上下导板附近产生了强剪切作用,破坏边界层的稳定性,激发大量羽流的产生,较大地增强系统传热.随着ω的增加,上下热边界层产生的羽流越来越多.在传热特性方面,该研究得到了Nu数和Ra数满足接近1/2的指数标度律关系,这表明系统的传热规律由经典的Nu∼Ra0.3标度行为逐步过渡到终极态标度行为Nu∼Ra0.5(见图7(a)和(b))[2].这一研究结果也给出了湍流终极态标度律存在的直接证据.当振动激励作用于湍流热对流系统时,流体速度一部分由振动诱导,另一部分来源于脉动速度.Wu等[38]采用相分解法,将振动产生的振荡流和脉动场区分开来,证实了振动的剪切效应可以增强速度脉动,从而促发热边界层的不稳定.

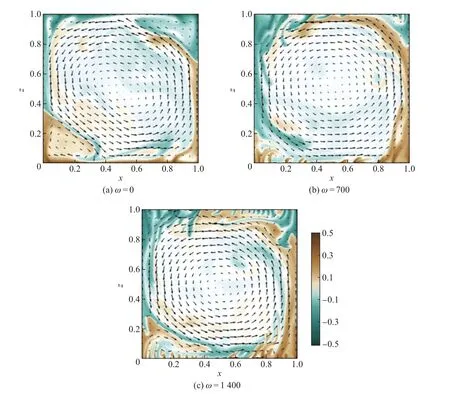
图6 不同频率ω下振动RB热对流中的流动结构Fig.6 Flow structure in vibrational RB convection at different frequenciesω

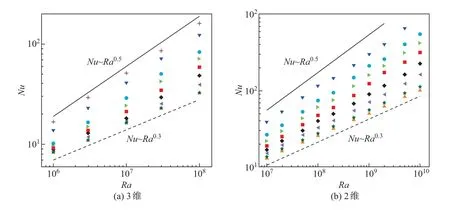
图7 振动RB热对流系统中不同频率ω下Nu随Ra的变化Fig.7 Plots of Nu as functions of Ra at different frequenciesωin vibration RB convection

2.2 振动侧壁热对流

振动侧壁热对流(VC)在自然界和工程中有许多应用,如使用双层玻璃窗(墙)进行隔热;在带有加热和冷却侧壁的水池中进行水平热传输[39];放射性废物容器的冷却、防火、太阳能收集、河口废热扩散和液体中的晶体生长等都存在着VC[40].这种对流系统也已被广泛应用于研究热驱动的大气[41-42]和海洋[43-44]环流中.图5(b)给出了2维振动VC系统的模型示意图.

Fu等[19]采用数值模拟方法研究了垂直振动下2维VC方腔内的热对流问题,发现在研究的频率范围(1≤ω≤104)内,随着ω的增大振动VC可以分为5个阶段:准静态对流阶段、振动对流阶段、共振对流阶段、中间对流阶段和高频振动对流阶段.通过比较Ra数和Ravib数,可以进一步了解不同流动区域下浮力与振动力之间的主导关系.研究结果发现:在高Ra数下(Ra=106),重力占主导地位,振动对传热效率的影响不显著;在低Ra数下(Ra=104)下,除准静态对流区外振动在对流中占主导地位.对于不同频率(ω=100,900,1 100,5 000)下瞬态热对流中流动结构的转变,Fu等[20]在随后的工作中做了详细的分析;Kim等[21]通过实验研究发现,在特定强迫频率下温度的波动幅值出现峰值,验证了VC系统的封闭腔体内重力波共振的存在,并且详细讨论了机械振动的幅值、频率和Ra数对共振的影响.随着Ra数的增大,共振频率单调增大,而机械振动幅值的增大对其影响较小.在VC系统中,振动方向的改变也会对系统的流动结构造成影响.Mokhtari等[22]和Bouarab等[45]研究了不同相位角振动下的VC系统的流动结构,发现在0∼π/4下,流动强度随着角度的增大而增强,并且在π/4时达到最大值(见图8(b)).特别地,在π/2∼π区间内的特定角度下,他们观察到了流动反转现象(见图8(a))[45].Guo等[3]进一步研究了更高Ra数(108≤Ra≤1010)下的垂直振动VC,以观察在振动激励下VC系统内激发的湍流态.研究发现系统存在一个临界振动频率ω∗,临界振动频率ω∗与Ra数的标度律关系为ω∗∼Ra−0.16(见图9(a))[3].当ω<ω∗时,振动对对流流动的影响很小;当ω>ω∗时,高频振动在近壁区域诱发了强烈的剪切效应,促进了羽流的喷发,导致主区流动从层流向湍流的转变(见图10)[3].流动状态的转变,也使得Nu数和Ra数的标度律关系由传统VC系统中的Nu∼Ra−0.25转变为Nu∼Ra−0.42,Re数和Ra数的标度律关系也由Re∼Ra−0.37转变为Re∼Ra−0.52(见图9(b)和(c)).

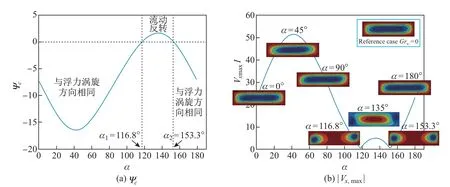
图8 振动VC系统腔体中心截面流函数Ψc及最大绝对水平速度|Vx,max|随振动角度α的变化Fig.8 Plots of stream functionΨc and maximal absolute horizontal velocity|Vx,max|at the mid-height as a function of the vibration angleαin vibrational VC system

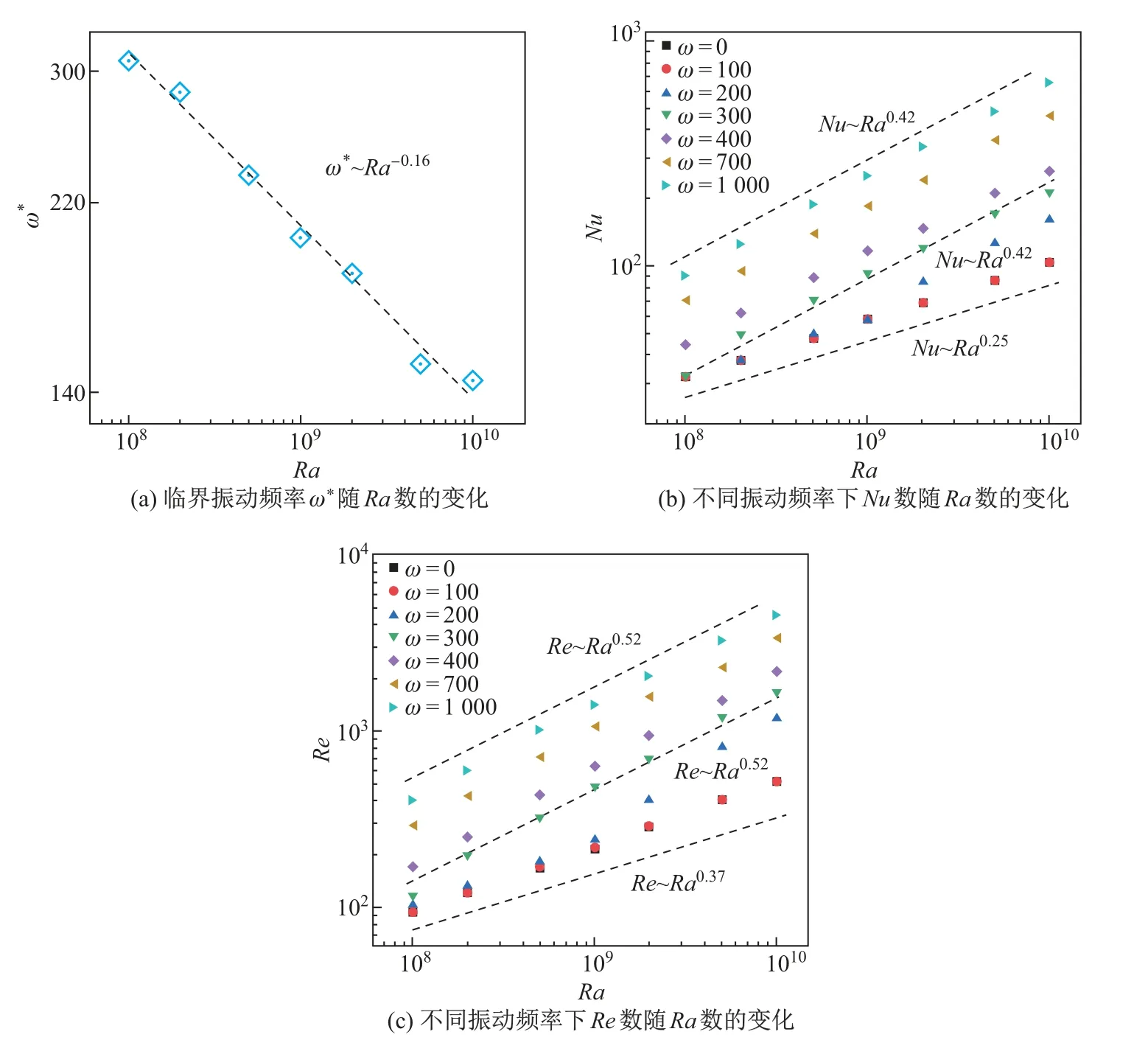
图9 振动VC系统中传热效率和流动强度随控制参数的变化Fig.9 Variation of heat transfer efficiency and flow intensity with control paramaters in vibrational VC system

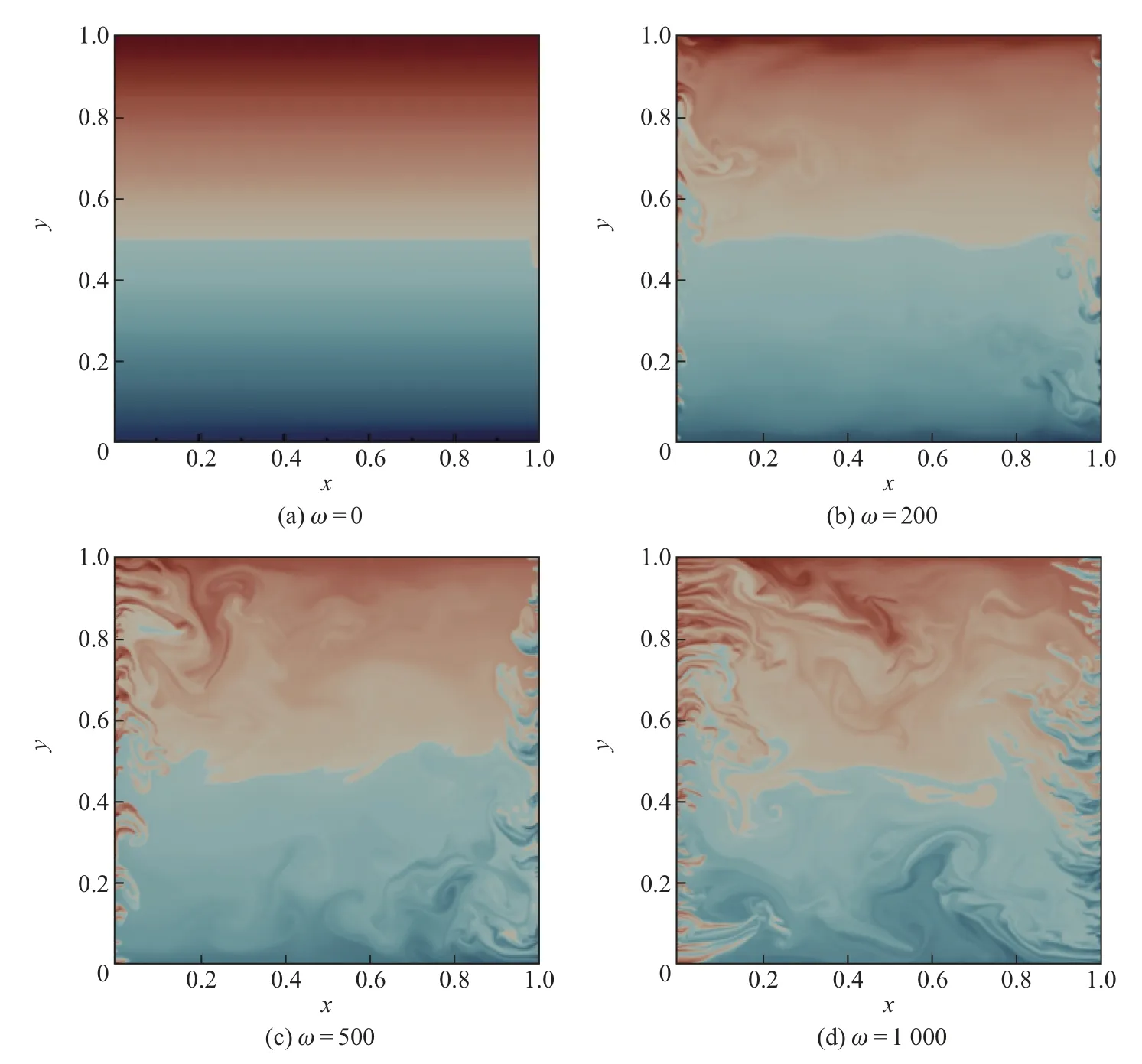
图10 不同频率ω下振动VC系统中的流动结构Fig.10 Flow structure in vibrational VC system at different frequenciesω

2.3 振动水平热对流

振动水平热对流(HC)不同于RB对流以及侧壁VC[46],其底板施加的温度为线性变化,上导板及侧壁均为绝热边界条件(见图5(c)).HC的研究在地球物理和地质流体力学领域具有重要意义,如行星大气流动和混合[47]的研究、河流中物质输运[48]和大尺度海洋环流[49]的能量交换,以及玻璃溶解和制造业[50]等工业应用.在自然系统和工业生产中,振动是不可避免的影响因素之一.杨添咏[23]通过数值模拟研究了受振动激励的HC,发现一旦超过临界振动频率ω∗,水平振动对系统的传热开始有明显的提升,并且临界振动频率ω∗随着Ra数的增大而减小(见图11(a)和(b)).在较高的Ravib下系统传热效率有明显的提高,Ra数越大传热增强的区域向着更大的Ravib数移动,临界随着Ra数的增大而减小(见图11(c)和(d)).

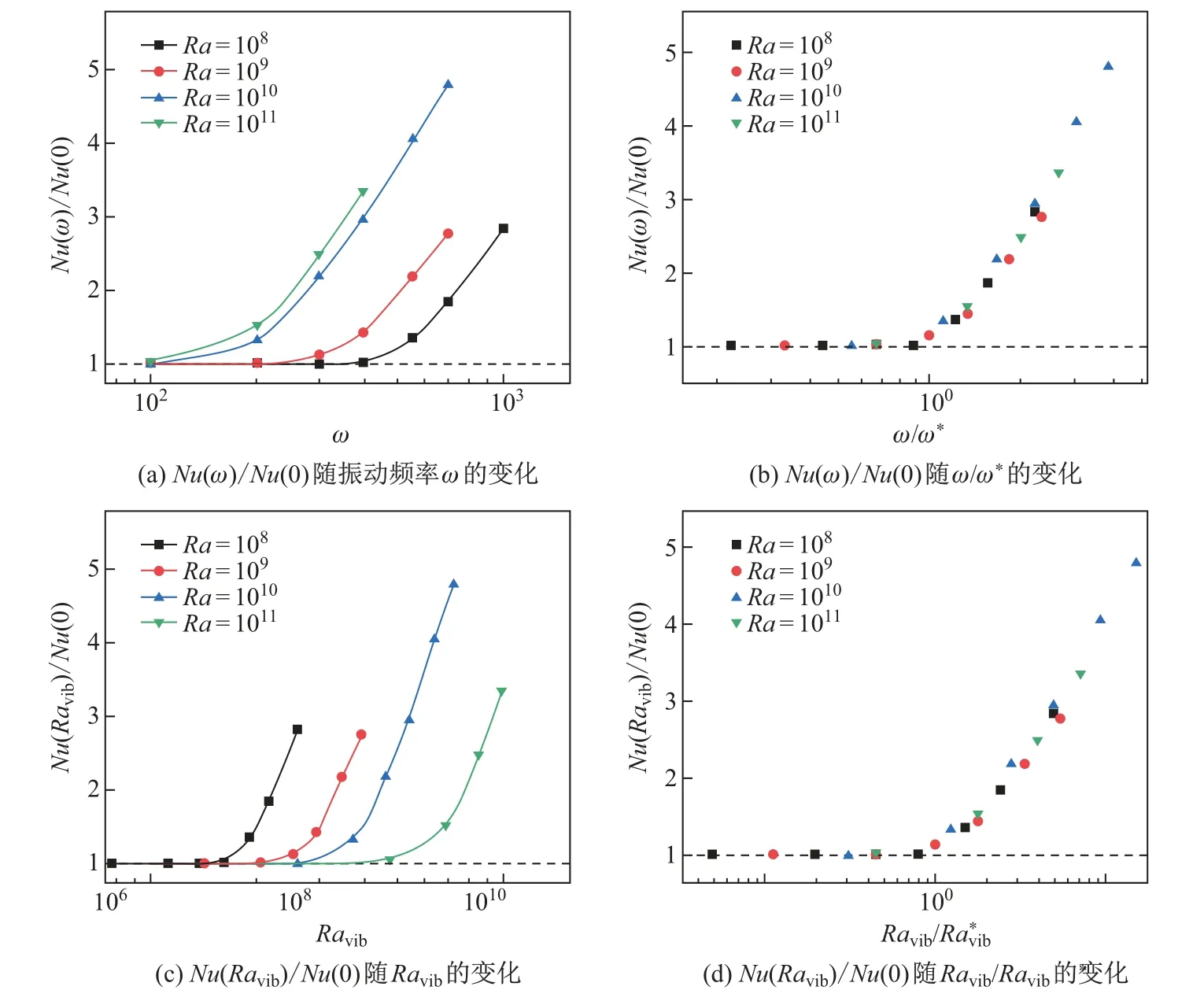
图11 Nu(ω)/Nu(0)和Nu(Ravib)/Nu(0)随不同振动参数的变化Fig.11 Plots of Nu(ω)/Nu(0)and Nu(Ravib)/Nu(0)as functions for the different control parameters

3 多相振动热对流的研究

多相振动热对流是一种具有2种或2种以上分散相物质体系的流体流动.在重力条件下,多相流中许多行为会受对流、沉降、分层等因素干扰,而微重力条件则有助于研究在地面上被重力作用所掩盖的过程,特别是多相间的相互作用.微重力多相流研究包括:胶体的聚集和相变研究、悬浮液和乳状液的稳定性研究、复杂等离子体的结晶研究、气溶胶的稳定性和聚集行为研究,以及对颗粒体系本征运动的研究等[51-54].

空间科学实验不仅能够获得新的科学发现,而且其科学成果对地面材料及器件制备工艺的创新具有重要指导意义.例如,对颗粒流中自组织现象的研究成果已经应用于纳米结构材料和器件的研制[55-56].在重力环境下,颗粒流中不同颗粒的分离现象一般受2种作用的制约,即重力和碰撞.在地面实验中,研究人员无法完全排除重力的影响而单独研究碰撞对诸如颗粒分离、富集的作用.微重力下颗粒流研究将有利于揭示这些现象背后的物理机制.20世纪90年代欧洲空间局科学家Folkersma等[57]利用探空火箭实验发现,在微重力条件下颗粒聚集速率要比地面条件下快11.2倍,这与人们的传统认识大相径庭.Pushkin等[53]通过粒子图像测速(particle image velocimetry,PIV)技术实验和数值模拟观察到,单个粒子的惯性和黏性力的相互作用可以导致粒子有序地形成动态螺旋结构.每个相干结构在有限的控制参数范围内是鲁棒的,一旦超出参数范围相干结构就会分散.Lappa等[54-55]采用直接数值方法,结合考虑惯性和黏性阻力影响下粒子运动的特定粒子跟踪方法,在Marangoni对流模型下研究了振动方向和不同振动幅值和频率下对颗粒分布的影响,通过振动激励的手段来控制颗粒富集结构(particle accumulation structure,PAS)的产生和消失(见图12).在特定的振动条件下,最初在液体中均匀分布的颗粒会发生偏离,然后形成一个有规律的三叶形的一维环状结构,并且沿着环形轴旋转.这种现象被称为动态粒子富集结构.

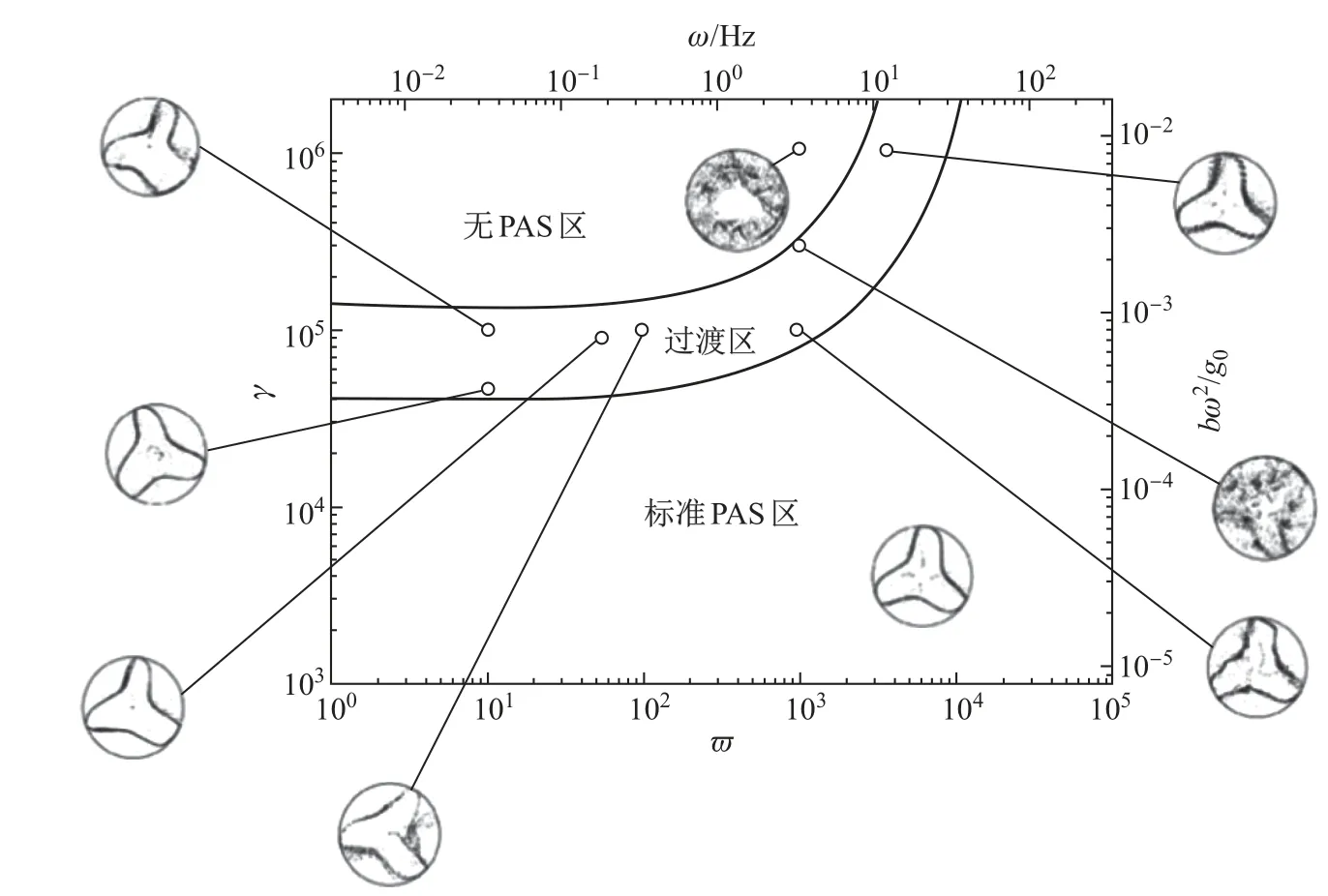
图12 在垂直于液桥轴线的重力跳动情况下PAS的发生与加速度振幅γ和频率ω的函数关系图Fig.12 Map for the occurrence of PAS as a function of acceleration amplitudeγand frequency ωin the case of g-jitters perpendicular to the axis of the liquid bridge

多年来,黏弹性流动一直是学术界和工业界都感兴趣的主题,也是多相流研究关注的重点.黏弹性流动因其在晶体生长、注射成型、化学物质运输和石油工业等制造过程中频繁出现而受到关注.Yang[58]研究了振动激励对黏弹性流的热不稳定性的影响.对于振动激励下的牛顿流,在低频下有不稳定效应,在高频有轻微的稳定效应,且随振动振幅的增大而增大.在黏弹性流体中,振动激励在低频和高频范围内的作用与牛顿流体相同.而在中频范围内,振动产生的次谐波扰动对较小的Deborah数和较大的Deborah数的稳定都有增强作用.Boaro等[59]对振动激励下黏弹性流进行了完整的参数研究:随着Ravib数的增大,黏弹性流体与牛顿流体有着不同的振动热对流模式.由于外部振动和聚合物分子的弹性特性之间的复杂互动,在黏性效应的作用下可以产生有趣的间歇性反应.如图13所示,初始时刻有3个涡结构,随着时间演化,流场中最多出现了12个涡结构;在3/8周期时又回到了三涡结构的状态.

图13 振动多相热对流中非牛顿流体流动结构在振动周期内的时间演化(T为振动周期)Fig.13 Time evolution of non-Newtonian fluid flow structure in vibrational multiphase thermal convection in vibrational period(T is the vibrational period)

4 总结与展望

在微重力环境下,振动激励可以作为一种新的驱动机制来实现物质和热量的输运.从这个意义上说,振动驱动机制可以实现一种人造重力.现有研究表明,小振幅和高频振动可以产生人造重力,Rubin等[60]指出,对宇航员的腿和脚施加振动产生人造重力,可以防止长时间在太空中生活导致的肌肉萎缩和骨骼脱钙.在地表重力环境下,振动激励作用于不同的热对流系统时可以改变系统的稳定性,控制流动结构的生成演化过程和系统传热.研究结果表明,振动方向、频率和振幅对系统的传热特性和流动结构产生了不同程度的影响.根据振动与温度梯度间的相对方向,振动可以产生或延迟对流的不稳定性.当振动方向平行于温度梯度方向时,振动激励产生的人造重力会抵消掉部分重力加速度,从而减小系统受到的浮力,对腔内的流体起到了致稳的作用.而当振动方向垂直于温度梯度方向时,振动产生的剪切作用促进了对流腔体内温度边界层的失稳,流动状态也相应发生转变,流动的对流换热效率随着振动强度的增强而提高.在多相振动热对流研究中,振动激励为研究和控制多相流动提供了新的思路.通过在颗粒流施加外部振动激励,颗粒可以直接获得动量.根据振动的方向,振幅和频率可以进一步控制颗粒富集结构的分布.此外,施加振动激励可以控制黏弹性流动表现出与牛顿流体流动不一样的流动结构,并改变其对流模式.

尽管目前研究人员已经对振动驱动热对流系统进行了大量的研究,但是仍然存在很多亟待解决的问题:①在以往的研究中,对微重力下小振幅高频率振动的流动结构以及失稳过程的关注较多,而在微重力下振动驱动热对流的传热特性及其物理机制仍未明确;②在地表重力环境下可以通过施加振动激发流动向湍流态转变,然而目前仍未观察到微重力环境下振动热湍流现象,因此对于湍流状态下振动热对流中能量跨尺度传输特性和物理机制有待进一步研究;③不同流体介质,即Pr数对振动驱动热对流的流动结构生成演化过程和传热规律的影响有待进一步研究;④多相振动热对流由于其具有重要的工程意义和学术价值得到广泛的研究,但是对于相间动量和能量输运过程的研究仍较少,因此多相振动热对流中振动激励产生平均流动对多相间相互作用的影响及其机理,是今后值得研究的重要课题.

致谢感谢清华大学孙超教授对本工作的大力支持.