高精度双向同步旋转CORDIC算法设计与实现
2022-12-06郑传喜古元冬
郑传喜古元冬
(1.上海大学微电子学院,上海 201800;2.上海微技术工业研究院,上海 201800)
坐标旋转数字计算机(coordinate rotation digital computer,CORDTC)算法是硬件系统中非常重要的一种算法,主要用于三角函数、双曲线函数、指数函数以及对数函数的运算[1].在精密电机数控系统中存在大量的三角函数运算,由于CORDIC算法具有较强的可移植性、实现简单以及精度可控等特点[2-4],被广泛应用于电机控制领域.
目前电机控制领域中CORDIC算法的设计通常为16位输出精度的正余弦值输出,平均误差为10−5∼10−4,但随着精密电机控制领域中对Park变换精度要求越来越高,需要在16位位宽下得到更高精度的输出.传统CORDIC算法的改进主要集中在缩放因子、角度收敛以及迭代方式等方面.Kulshreshtha等[5]通过滑动离散傅里叶变换(discrete Fourier transform,DFT)与Hann窗相结合,对缩放因子进行补偿,提高了输出精度,但硬件实现结构较为复杂.Shukla等[6]提出了一种混合型算法,将双步分支CORDIC算法和radix-4 CORDIC算法相结合,而Garrido等[7]舍弃了传统CORDIC算法中使用的角度,引入了友角(friend angles),二者都提高了旋转角度的收敛速度,但是输出精度较低,需要通过增加额外的迭代次数来保证精度.徐成等[8]通过多步合并迭代降低了输出时延,但精度并无明显提升,姚亚峰等[9-10]通过大量查找表来降低输出时延,但存在硬件资源消耗大等问题,之后将旋转过程分为粗旋转以及细旋转,避免了缩放因子的引入,节省了资源消耗,但精度提升仍有限,
针对上述问题,本研究对CORDIC算法存在的精度以及延时问题进行改进,设计了高精度双向同步旋转CORDIC算法.该算法先对角度进行预处理,再根据查找表对输入角度进行双向同步旋转,同时,在迭代过程采用双步旋转,以此减少输出延迟和部分硬件资源消耗,最后通过误差均衡和还原输出,提高整个算法的稳定性.仿真结果表明,本改进算法具有低延迟、高精度以及稳定等特点,更适合对实时控制和精度有更高要求的精密电机控制系统.
1 高精度双向同步旋转算法
CORDIC算法的基本原理是将目标角度分解为若干角度,然后通过一系列的旋转来接近目标角度.引入,并对θi进行一定的限制,令θi=arctan2−i,其中di={1,−1},di=1表示向量是逆时针旋转,di=−1表示向量是顺时针旋转[11].其迭代过程如下:
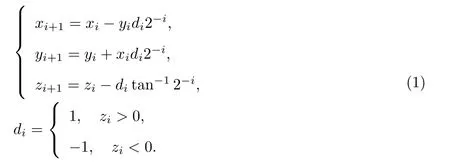
由式(1)可知,CORDIC算法只需通过简单移位和加法运算便可实现,而传统算法存在输出时延高、硬件资源消耗大以及运算精度低等问题.针对上述问题,本工作提出高精度双向同步旋转算法,该算法首先对16位的输入角度进行重编码和区间判断,然后计算迭代目标角度,并将其送入迭代器中进行双向同步旋转和误差均衡,最后根据区间编码值对正弦和余弦进行还原处理.
1.1 角度预处理与区间折叠
本改进算法采用13位小数位、2位整数位、1位符号位共16位二进制补码表示输入角度.对于传统CORDIC算法,由于0≤sinθ≤1,0≤cosθ≤1,且{max(θ),min(θ)}≈{99.9◦,−99.9◦},因此无法覆盖整个圆周.根据三角函数的周期性以及对称性,可以只计算[0,π/4]的值便可覆盖整个圆周[12].因为π/4<1,且在θ∈[0,π/4]时,0≤sinθ≤1,0≤cosθ≤1,因此迭代目标角度可以采用13位无符号数表示,即,而最终输出值则使用16位有符号数表示,这样可以适当减少寄存器的消耗.表1表示了从[0,π/4]映射到[0,2π]的过程,其中前3列表示了角度预处理的过程,后2列表示对结果的还原处理.
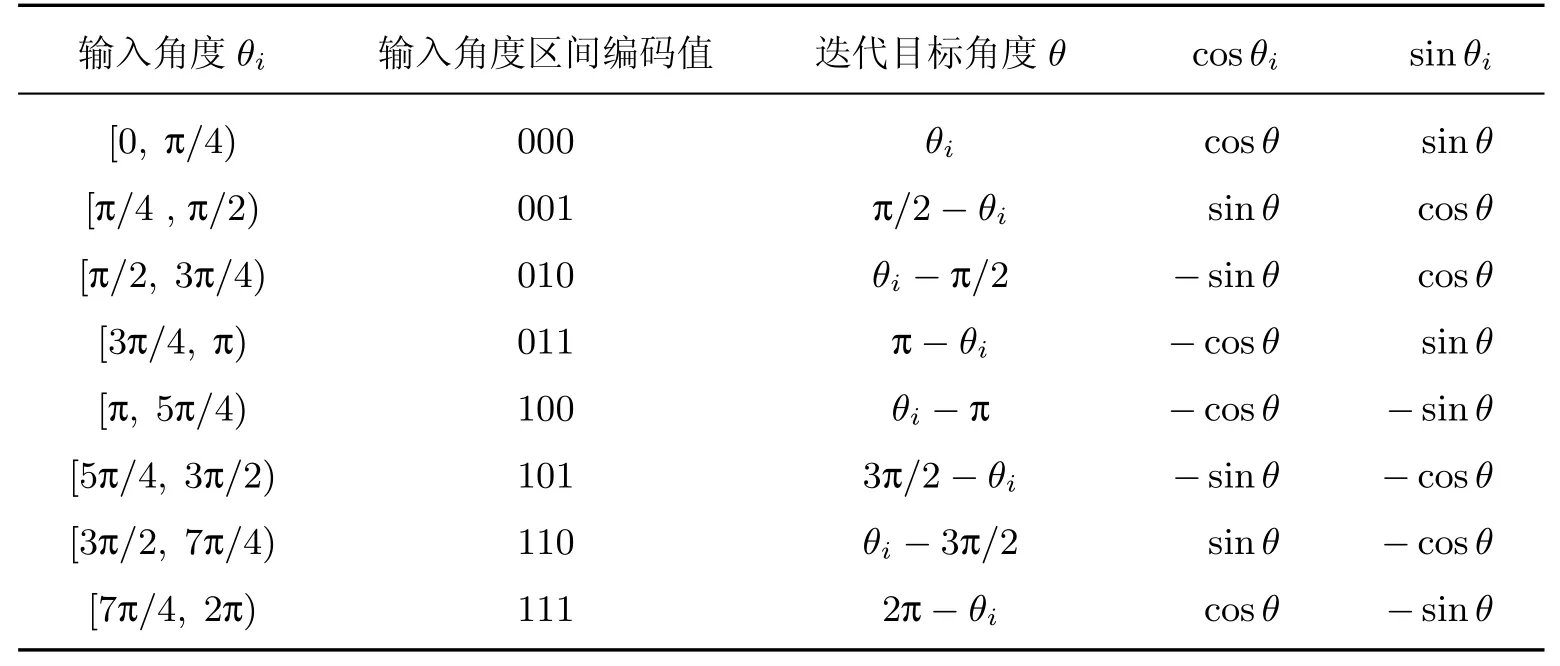
表1 角度预处理与区间折叠Table 1 Angle preprocessing and interval folding
对于区间编码值和迭代输出结果的关系,首先判断区间编码值(从右往左)的第1位和第2位,如果不同,则表示迭代计算完成后得到的正弦值和余弦值需要进行交换,否则不需要交换;然后判断第2位和第3位,如果不同,则余弦值取反,否则不取反;最后判断第三位,如果为1,则对正弦值取反,否则不取反[13].通过采用区间折叠,可以大大减少查找表的大小,保证输入角度能够覆盖整个圆周,增强了算法适用性.
1.2 查找表建立
通过角度预处理,可以将整个迭代区间压缩至[0,π/4],用13位二进制补码表示输入角度0X0000到0X1922.取区间前5位从00000到11001的角度,令后8位取0构成逆时针旋转表,令后8位取1构成顺时针旋转表,其旋转过程如图1所示.将弧度[0,0.781 25]分成了25小区间,每一个小区间宽度仅有1/32弧度,查找表中分别存储节点值对应的正余弦值,以此进行查表旋转.为减少查找表的消耗,对顺时针旋转时的正余弦值进行分析.
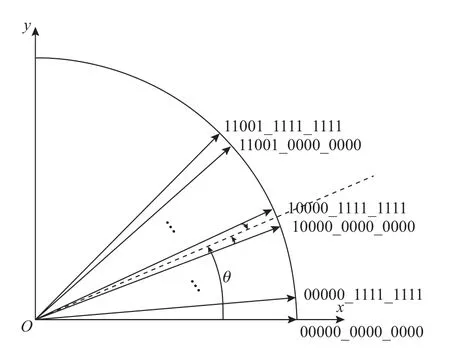
图1 双向同步旋转示意图Fig.1 Bidirectional rotation diagram
设逆时针方向角度前5位00000~11001的角度为α0∼α25,同理顺时针方向角度为β0∼β25,则存在以下关系:
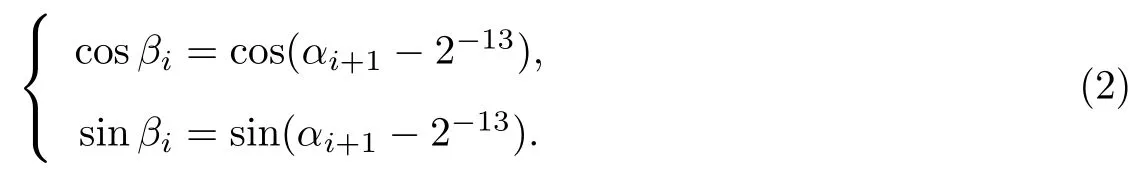
对于13位二进制数表示的小数,存在cos 2−13≈1,sin 2−13≈2−13,因此经过化简,最终可得

由式(3)可知,对于顺时针旋转表,只需在逆时针旋转表中增加前5位为11010的角度的正余弦值便可得到,不需额外重新制表.表2为逆时针旋转表.

表2 逆时针旋转表Table 2 Counterclockwise rotation table
1.3 双向同步旋转原理和误差均衡
双向同步旋转可以看作对目标角度进行逐位双向逼近的过程,在[0,π/4]内,n位二进制小数的角度θ可表示为2−1,2−2,2−3,···,2−(n−1),2−n的线性组合,即,其中ai={0,1},对应角度二进制小数位.根据余弦函数的性质
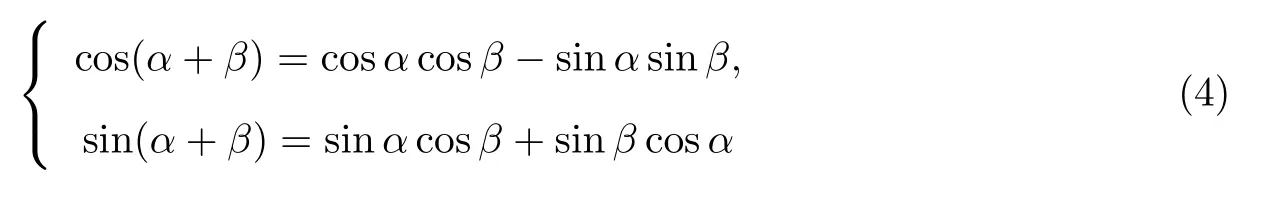
可知,第k+1次迭代可表示为
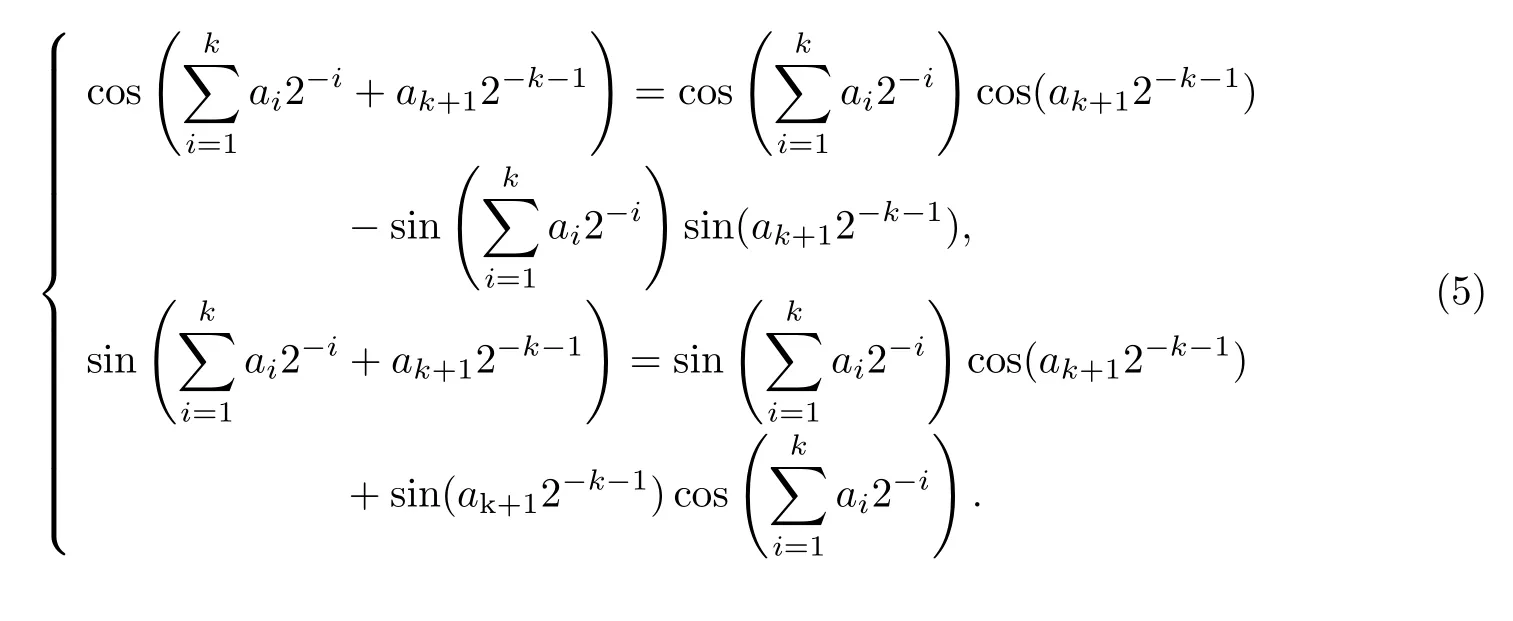
令θ=2−i,由正弦泰勒展开式可知,n位二进制数能表示的精度是有限的.考虑正弦函数的三次项,当i满足(i为整数),n=16时,解得i≥5,表示由输入角度小数位后8位计算的正弦值其精度已经不能正确表示到三次项[14].角度值的前5位的旋转可用查表法实现,因此可以忽略对缩放因子的计算.令第k+1次逆向旋转的余弦值和正弦值分别为,旋转微角度为,对式(5)进行化简,得到如下逆时针迭代式:
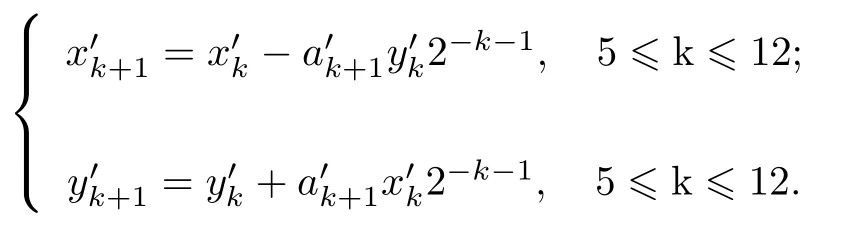
图2为逆向旋转硬件结构图,其中Shifter表示移位器,ADD/SUB表示加法器/减法器,当为1时,从左向右分别为减法器和加法器.
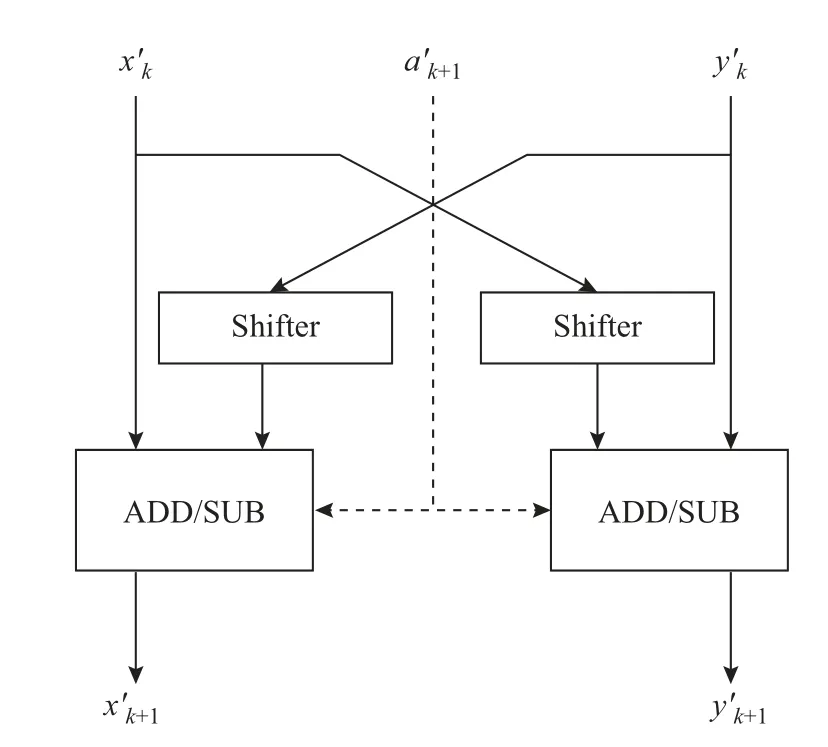
图2 逆时钟旋转硬件结构图Fig.2 Counterclockwise rotation hardware structure diagram
顺时针旋转的过程是对角度二进制数小数位的逐项相减的过程,整个迭代过程以及硬件结构都与逆时针时相似.顺时针迭代式为
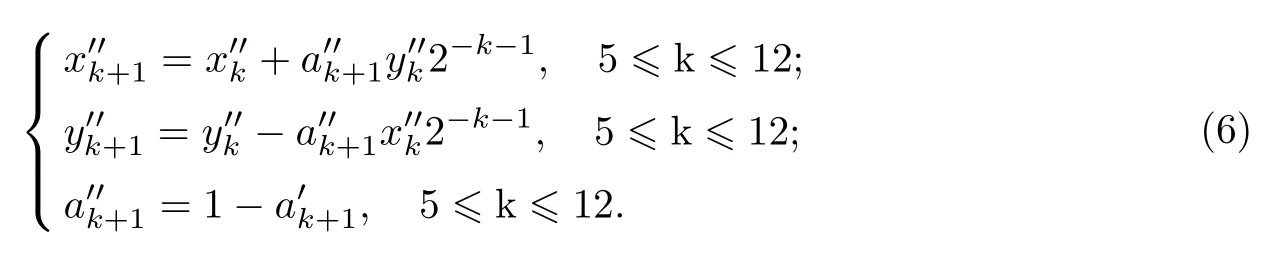
由式(6)、(7)和表2可知,逆向旋转随着角度增大,每进行一次查表,其误差都会达到更小.在两次查表之间,每当=1时,余弦函数将会与·1进行一次等效,其结果将大于真实值,因此,其误差也会逐渐增大,而顺向旋转则相反.
在整个迭代过程中同时进行顺时针旋转和逆时针旋转,然后对输出结果进行误差均衡处理,则最终结果可表示为

双向同步旋转可以忽略对缩放因子的计算,引入逐位双向逼近的概念,当旋转方向确定后,每次旋转的角度和角度二进制数每一位都相互对应,避免了传统CORDIC算法在已经旋转到正确角度时,由于每次旋转角度已经固定,依然会继续旋转而引入的误差.传统算法的精度和迭代次数正相关,误差主要取决于3点:①将θ和tanθ进行等效而带来的误差;②查找表带来的截断误差;③旋转因子引入的误差[15].因此为了保证相应的精度,传统算法需要较多的迭代单元和迭代次数,但本工作提出的改进算法首先通过查表旋转来避免旋转因子的误差,其次没有将θ和tanθ进行等效,而是利用泰勒展开式直接对正余弦进行等效,进一步减少误差.同时,在旋转迭代过程完成后,本改进算法会对结果进行误差均衡处理,降低了误差曲线抖动,提高了整个算法的精度和稳定性.
1.4 双步旋转策略
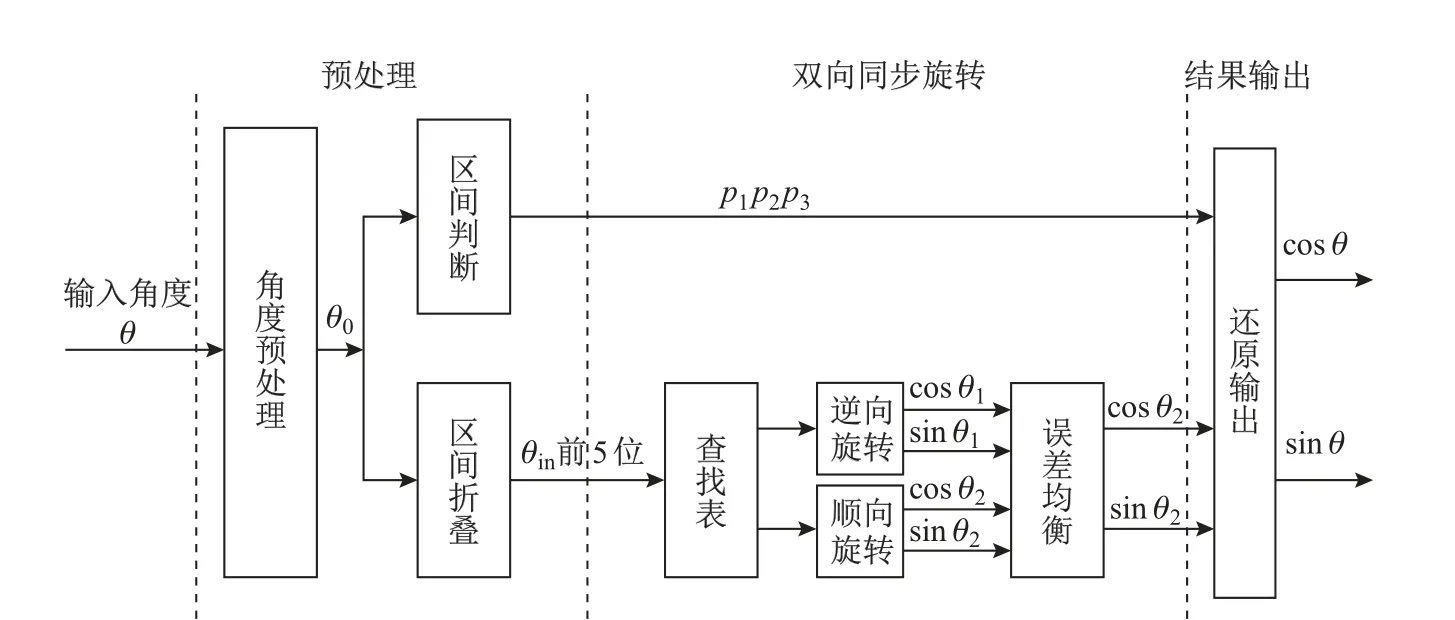
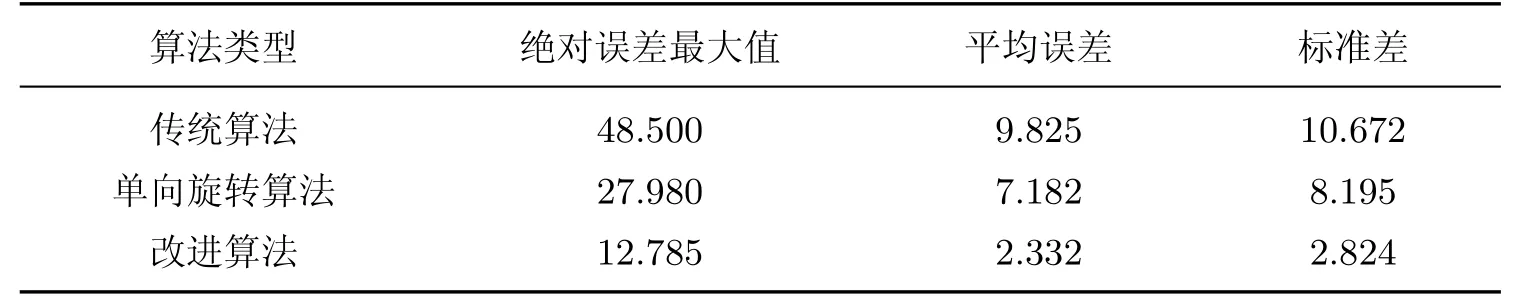
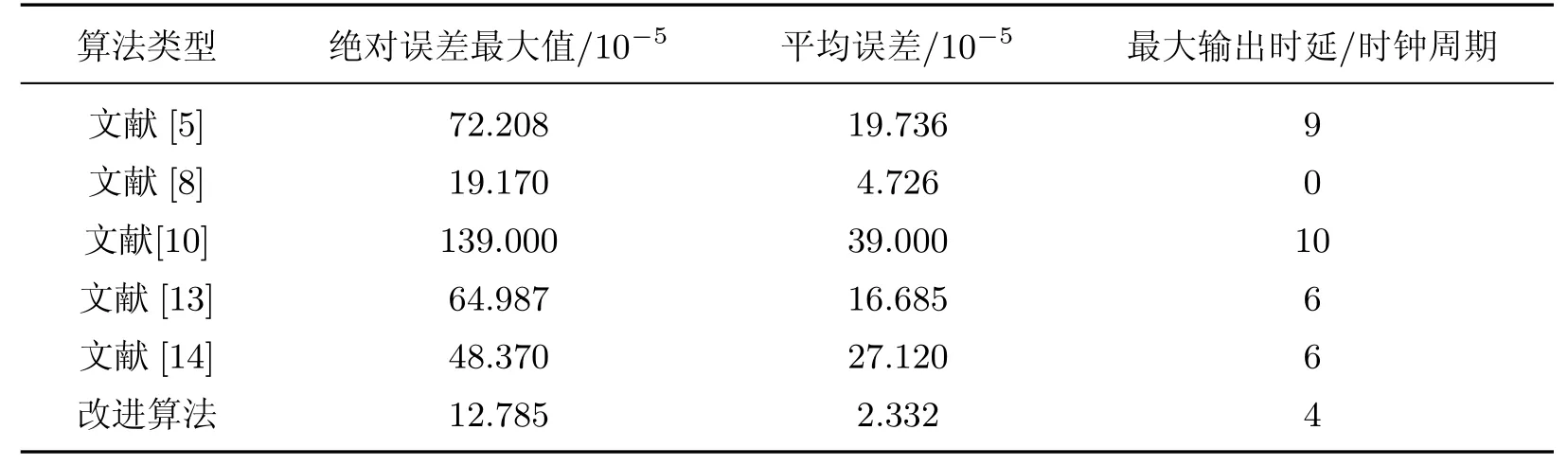
双步旋转的基本原理基于输入角度在迭代前便可以知道旋转方向以及旋转角度的大小,因此可以将两次旋转进行合并,通过这种方式来达到减少迭代次数的目的,从而可以适当减少资源消耗并降低输出时延[8].对于逆时针旋转,假设两次旋转的角度分别为θi=ai2−i和θj=aj2−j(i 双步迭代矩阵可以表示为 在本改进算法中,令j=i+1,结合式(6),对式(9)进行化简,可得 当i≥(L−1)/2时,上述参数又可简化为α=ε=1,γ=−β=ai2−i+aj2−i−1,其中L为数据位宽. 通过上述推导,可以将两步迭代简化为一次,且只需通过加法和移位操作便可完成.在i≥(L−1)/2的情况下,算法的结构可还以进一步简化,因此相比单向旋转算法,本算法可以极大的减少迭代次数,进而降低输出时延. 本改进算法的硬件实现主要包括预处理、双向同步旋转、结果输出共3个模块.预处理模块主要完成对角度二进制编码,并对输入角度进行区间判定以及将输入角度映射至[0,π/4].双向同步旋转模块主要完成对角度进行双向迭代和误差均衡,旋转过程采用4级流水线设计,最终产生经过角度折叠后的正余弦值.结果输出模块主要根据区间对正余弦值进行还原输出.采用Verilog HDL语言进行硬件设计,图3为算法的硬件结构框图. 图3 硬件结构框图Fig.3 Block diagram of hardware structure 首先结合表2和式(6)∼(8),利用Matlab对改进算法进行建模仿真,并与传统算法、单向旋转算法进行对比,结果如图4所示. 图4 第一象限余弦误差算法仿真图Fig.4 Algorithm simulation diagram of the first quadrant cosine error 从图4可以看出,顺向算法在经历了一次查表旋转后,其误差将会逐渐降低,而逆向旋转则刚好相反,正因为该特性,改进算法可以通过误差均衡在单向算法的基础上进一步提高精度.表3为余弦函数仿真误差的对比.由表3可知:相比传统算法和单向旋转算法,改进算法的绝对误差最大值分别降低了73.3%、60%,平均误差分别降低了47.0%、45.3%,标准差分别降低了60.2%、55.5%. 表3 余弦函数仿真误差对比Table 3 Cosine function simulation error comparison ×10−5 为了验证改进算法的实际性能,在Xilinx公司XC7K160T-1FBG676C型号的FPGA上对算法进行实现,并与传统CORDIC算法、单向旋转算法进行对比分析.在16位的位宽条件下,对输入角度以2−13的分辨率在第一象限进行遍历.图5为3种算法的误差分析结果,余弦函数误差对比结果见表4. 由图5和表4可以看出,相比传统算法和单向旋转算法,实际应用场合下改进算法的绝对误差分别降低了73.6%和54.3%,平均误差分别降低了76.3%和67.5%,标准差分别降低了73.5%和65.5%.主要原因是:改进算法吸收了单向旋转算法的优点,即当di为0时,可以避免不必要的旋转,减少误差累积;利用顺时针和逆时针旋转的误差特性进行误差均衡,弥补了单向旋转算法因区间折叠而在[π/4,π/2]区间上导致绝对误差的断层,进一步降低了平均误差和标准差. 图5 第一象限余弦绝对误差分析Fig.5 Cosine absolute error analysis in the first quadrant 表4 3种算法的余弦函数误差Table 4 Comparison of three cosine error algorithms 10−5 通过Vivado软件对3种算法进行逻辑综合,得到寄存器消耗个数、查找表消耗个数、最大输出时延以及最高运行频率,结果如表5所示.表6列出了近年来国内外部分文献中CORDIC算法与本改进算法的精度对比. 表5 3种算法的逻辑综合结果Table 5 Logical synthesis result of three algorithms 表6 CORDIC算法精度的对比Table 6 Comparison of CORDIC algorithm accuracy 由表5可以看出,改进算法相对传统算法,寄存器消耗个数下降了41.0%,查找表消耗个数下降了36.9%,最大输出时延降低了71.4%.相对单向旋转算法,由于改进算法同时进行了正向旋转和逆向旋转,因此最高运行频率相比单向旋转算法并无改善,但双步迭代使得迭代单元由单向免旋转算法的9级降低到了4级,最大输出时延降低了55.5%,而寄存器消耗量和查找表消耗量仅增加了19.9%、23.6%.与文献[5,8,10,13-14]提出的算法相比,本改进算法的平均误差降低是非常显著的,同时绝对误差最大值也有大幅度的下降(见表6). 本研究主要针对精密电机数控领域中16位位宽CORDIC算法精度不足、时延较长以及硬件资源消耗较大等局限做出改进,改进算法首先通过区间折叠来扩大角度计算范围,然后通过查找表进行一次查表旋转,再通过双向同步旋转和误差均衡进行迭代计算并以此降低误差,旋转过程中用双步迭代降低迭代单元级数,降低了输出时延,最后根据角度区间进行还原输出.在硬件实现上,相比传统算法和单向旋转算法,运算精度分别提高了76.3%和67.5%,最大输出时延降低了71.4%和55.5%.在硬件资源消耗方面,改进算法对比传统算法在寄存器消耗和查找表消耗方面分别下降了41.0%和36.9%,而相对于单向旋转算法,寄存器消耗和查找表消耗分别增加了19.9%和23.6%.本工作设计的改进算法具有高精度低延时等特点,因此更适合对精度和时延具有更高要求的电机数控系统.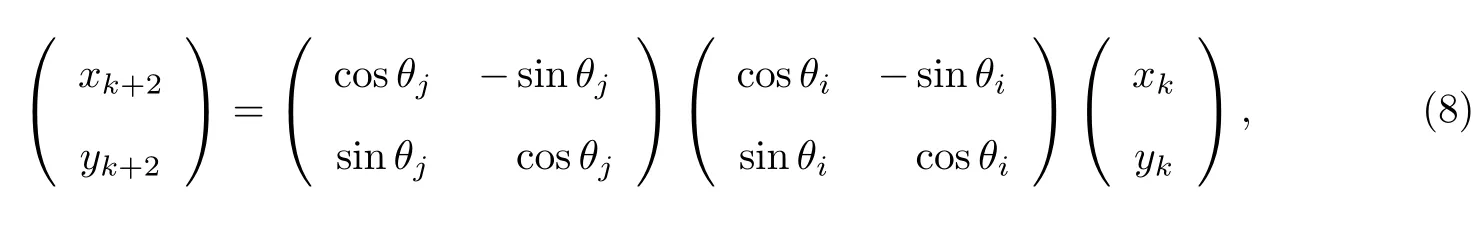
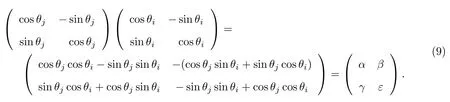
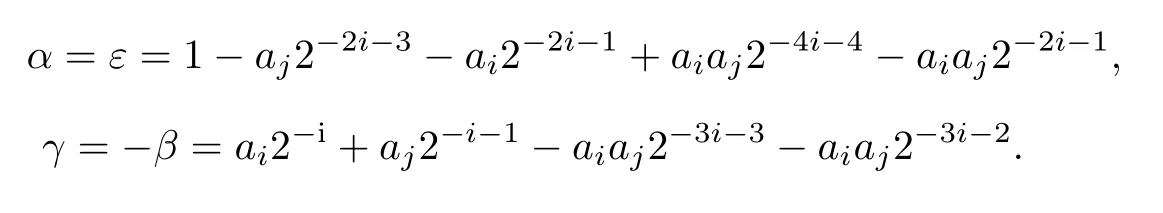
2 硬件设计
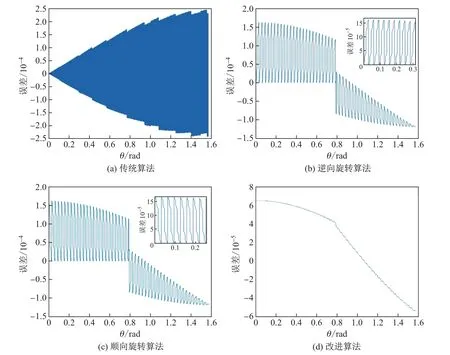
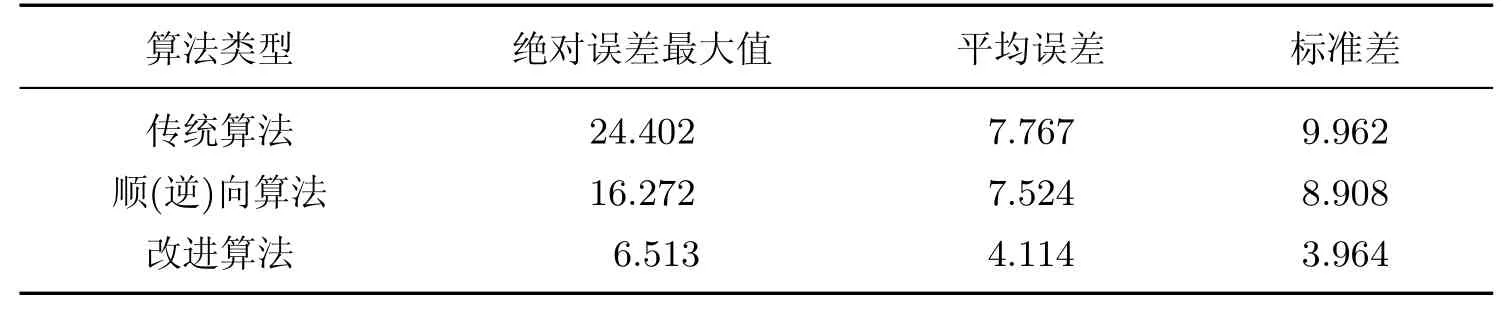
3 仿真及实验结果
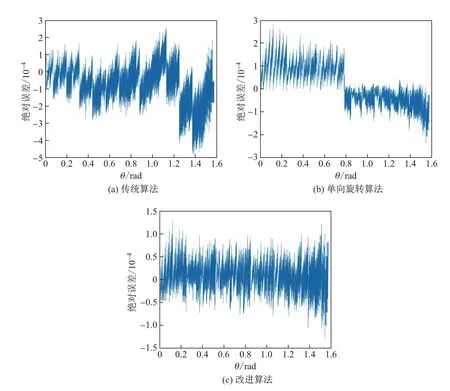

4 结语
