基于电流加热连铸恒温出坯温度场的分布与演变规律

郑天晴,徐燕,张云虎,翟启杰

(上海大学先进凝固技术中心,上海 200072)

连铸是现代钢铁生产的重要方式,由连铸工艺生产的钢铁占世界钢铁产量的90%[1].为了实现连铸坯质量提高、生产效率提升、生产能源节约等目标,已在连铸生产中开发了连铸坯热送直轧工艺.为了实现连铸坯的热送直轧,有必要保证连铸坯温度的均匀化,因此通常采用感应加热方法[2]对连铸坯表面和角部进行补热,从而降低连铸坯径向的温度梯度.

针对连铸坯感应加热这一课题,已开展了诸多研究工作.刘浩等[3]建立了连铸坯感应加热过程温度分布模型,研究了磁场频率对连铸坯温度分布的影响.Cho[4]建立了多线圈低频(60 Hz)感应加热预测模型,并验证了该模型下移动圆坯的加热效果.肖宏等[5]建立了感应补热有限元模型,分析了纵向磁场与横向磁场的补热过程.结果表明,纵向与横向磁场的协同作用对板坯起到了良好的补热效果.王学兵等[6]研究了连铸直轧过程中不同感应加热参数下铸坯温度场的分布规律.结果表明,铸坯横断面的整体温度随激励电流的增大而升高,且越靠近铸坯表面温度升高幅度越大.此外,还有研究表明,感应加热过程中热量存在诸多损耗,热效率为65%∼75%[7].

目前,电流已广泛应用于冶金行业.炼钢主要方式之一的电弧炉技术[8]即是利用电弧热效应直接加热并熔化金属.在冶炼高温合金时常用的电渣重熔工艺也同样是利用电流的热效应将金属重熔再凝固[9].电流在热处理中也有诸多作用.例如:电流的通入导致基体中电中性微粒发生旋转,从而产生理想的宏观各向异性[10].电流的通入还能细化金属凝固组织[11]、促进钛合金马氏体相变[12]、促进GH3030合金的静态再结晶[13]、大幅缩减镍基合金固溶处理时间并改变金属中有害共晶相的形态[14]、减少高强度合金中的氢含量[15]等.上述影响在改变铸坯组织形貌的同时,也提升了铸坯性能.

为了在实现恒温出坯的同时提高热效率,本工作提出了一种基于电流直接加热的均温化方法,即将中频交流电直接通入连铸坯中,利用电流产生的焦耳热直接加热连铸坯.首先,通过数值模拟手段揭示电流加热作用下连铸坯内部电流和温度的分布规律.然后,研究温度场随激励电流频率和连铸坯移动速度的演变规律.最后,提出电流加热功率估算模型,为确定实现恒温出坯所需的加热功率提供理论指导.

1 连铸电流加热恒温出坯原理及方法

连铸恒温出坯的目的是消除连铸坯径向与长度方向的温度梯度.连铸坯长度方向产生温度梯度的原因是连铸坯头部较早离开结晶器,在空气中暴露时间长、热量损耗多,而尾部最后离开结晶器,在空气中暴露时间短、热量损失少,从而产生头部温度低于尾部温度的现象.连铸坯径向产生温度梯度的原因是连铸坯表面与空气和二冷水直接接触,使得连铸坯表面热量损失多于芯部,从而产生表面温度低于芯部温度的现象.

为了消除连铸坯径向与长度方向的温度梯度,本工作提出了电流直接加热方法.该方法利用传动辊传输电流,通过电流的焦耳热效应加热连铸坯,最终降低了连铸坯径向和长度方向的温度梯度,从而实现了恒温出坯.相较于感应加热方法,基于电流加热的方法不存在线圈引起的热损耗,有利于提升加热效率.

图1为电流加热装置示意图.在连铸切割机后端传动辊表面设置石墨环,同时在连铸坯头部端面设置移动式石墨环,两组石墨连同其间的连铸坯环构成闭合回路.当闭合回路中通有交流电时,交流电产生的热效应将加热回路中的连铸坯.该方法之所以能实现连铸恒温出坯,是因为中频电流通入铸坯后产生趋肤效应,使得连铸坯表面电流大于内部,电流产生的焦耳热将提升连铸坯表面温度,最终降低了连铸坯径向的温度梯度.此外,随着连铸坯的运动,接入回路的连铸坯长度增加.由于连铸坯头部始终接入回路,因此电流对连铸坯头部的加热效果强于尾部,从而有效降低了连铸坯长度方向的温度梯度.

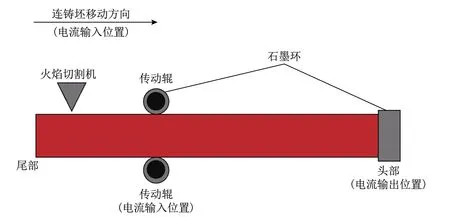
图1 电流加热装置原理图Fig.1 Schematic diagram of the current heating device

2 有限元模拟

2.1 几何模型及网格划分

基于第1节提出的电流加热连铸恒温出坯方法,采用有限元商业软件COMSOL Multiphysics建立了三维数值模型,如图2所示,其中域1为螺纹钢连铸方坯,方坯横截面边长120 mm,长度2 000 mm,域2为空气.连铸坯采用结构化网格,空气域采用非结构化网格.

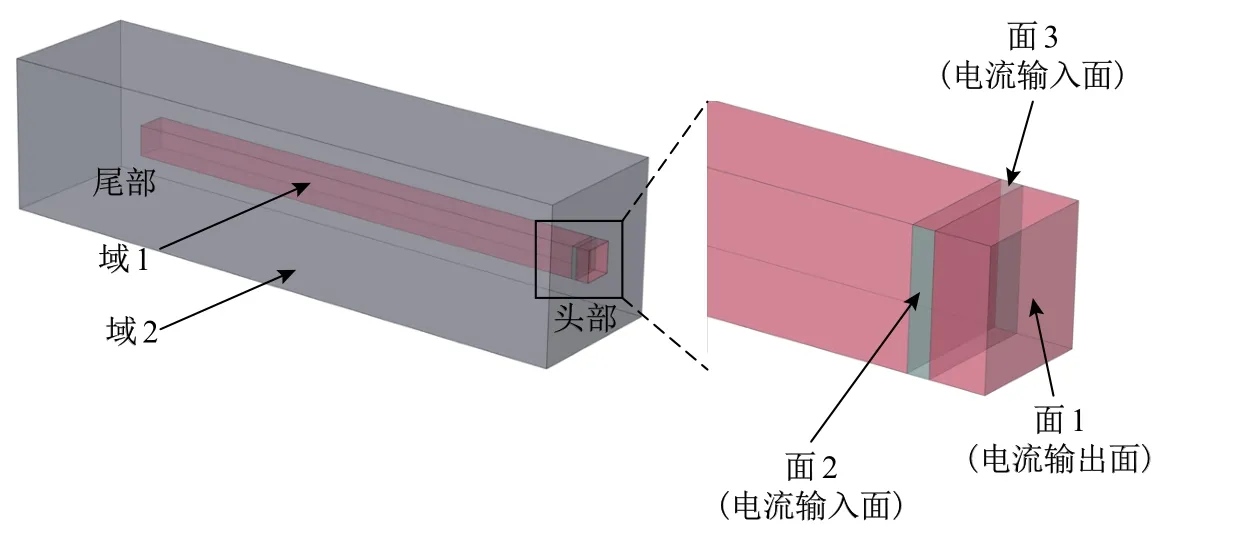
图2 基于电流加热的连铸坯数值模型Fig.2 Numerical simulation model of the continuous casting billet based on current heating

2.2 基本假设和物性参数

为降低模拟计算量和计算复杂程度,在模拟计算时对实际问题进行简化,并提出以下假设:①忽略连铸坯运动对磁场的影响;②连铸坯与外界的热量交换仅有热辐射和空气对流换热;③连铸坯物性参数随温度线性变化.模拟所用螺纹钢的化学成分如表1所示,该钢种的物性参数(密度、热导率、电导率和比热)如图3所示.在模拟过程中,连铸坯的温度区间为1 200∼1 500 K,其物性参数在该温度区间内线性变化.

图3 螺纹钢的物性参数Fig.3 Physical parameters of the screw-thread steel

表1 螺纹钢化学成分及质量百分比Table 1 Chemical composition and mass percentage of the screw-thread steel %

2.3 控制方程

2.3.1 电磁场控制方程

空间电磁场满足麦克斯韦方程组[16],即

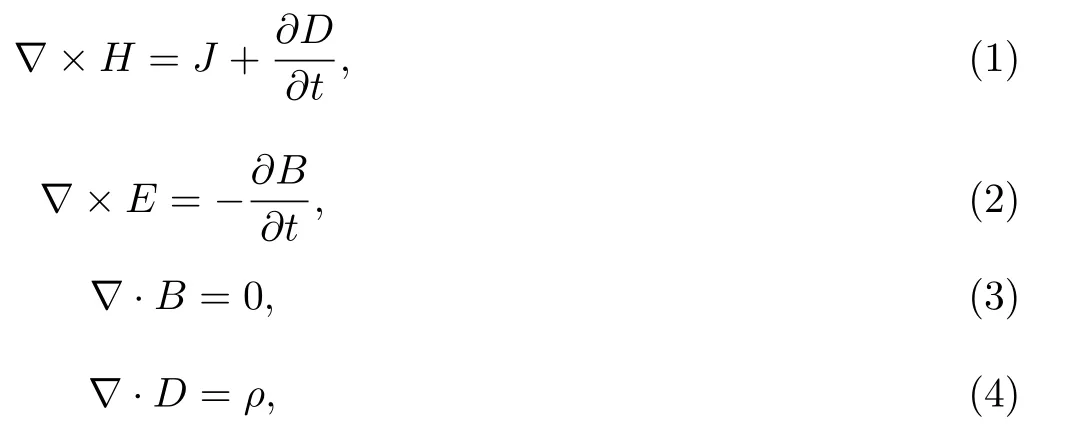
式中:H为磁场强度(A/m);J为电流密度(A/m2);D为位移电流(C/m2);t为时间(s);E为电场(V/m);B为磁感应强度(T);ρ为体电荷密度(C/m3).物理量之间满足以下本构关系,即

式中:σ为电导率(S/m);εr为相对介电常数;ε0为真空介电常数;µr为相对磁导率;µ0为真空磁导率.

在电磁场计算过程中,磁感应强度B和电场E可分别表示为

式中:A为矢量磁位(T·m);V为电势(V).

将式(5)∼(9)代入式(1),可得A的表达式为

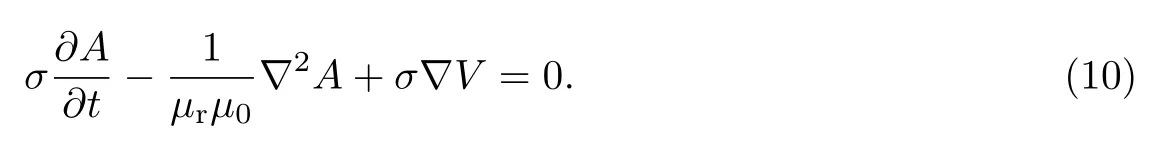
由于本工作中的电流为交流电,因此式(10)可进一步改写为频域方程,即

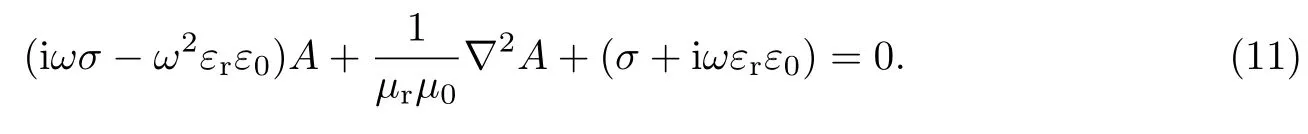
2.3.2 温度场控制方程

针对本模型中的固相连铸坯,其内部温度场满足热扩散方程[17],即

式中:ρ为连铸坯材料密度(kg/m3);Cp为连铸坯材料比热容(J/(kg·K));T为温度(K);q为热流密度(W/m2);Q为热能密度(W/m3).

2.4 初始条件和边界条件

2.4.1 初始条件

当连铸坯运动至火焰切割机位置时,连铸坯内部已存在温度梯度.为了在模拟中展现连铸坯沿径向和长度方向的温度梯度,人为设置连铸坯初始温度为

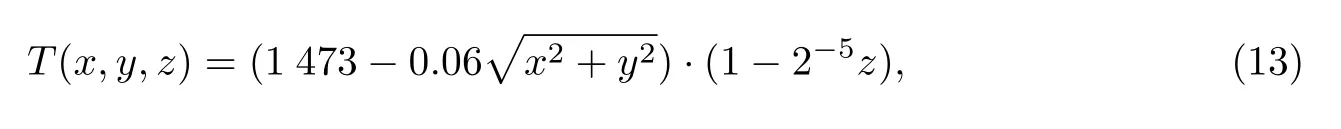
式中:x,y,z为笛卡尔坐标系中的坐标值;T(x,y,z)为连铸坯温度.

将轧辊与连铸坯接触区域(见图2中的面2、面3)设定为电流输入面,将连铸坯顶部区域(见图2中的面1)设定为电流输出面,以此约束电流输入输出面.

2.4.2 边界条件

在电磁场计算中,需满足以下条件:空气域边界满足磁绝缘条件,即矢量磁位的法向分量为0;连铸坯-空气界面满足连续性条件,即矢量磁位的切向分量相等;连铸坯头部设置为磁绝缘条件,并将其电势设置为0.

在温度场计算中,连铸坯-空气界面和连铸坯头部端面满足的温度条件为

式中:h为界面换热系数,取20 W/(m2·K);Tenv为环境温度,取293 K;T1为连铸坯不同位置的温度.此外,连铸坯表面存在辐射换热,即

式中:n为连铸坯表面外法线单位向量;ε为连铸坯表面黑度,在模拟计算中取经验值0.8;σ0为Stefan-Boltzmann常数,在模拟计算中取5.67×10−8W/(m2·K4).

由于连铸坯尾部在连铸坯切割前始终与二冷区相连,故不存在与空气的换热.因此,将该边界设置为绝热条件.

2.5 求解方法

在计算连铸坯内部电磁场和温度场时,首先计算不同电流输入位置空间中的电磁场,然后采用移动热源法,将不同电流输入位置计算所得的焦耳热作为热源代入温度场控制方程,求解连铸坯的温度场.计算电磁场时,采用频域求解器;计算温度场时采用瞬态求解器,计算子步为1 s.

3 结果与讨论

3.1 电流加热作用下,连铸坯内部的电流、温度场分布规律

3.1.1 电流分布规律

当连铸坯移动速度为1.2 m/min,激励电流频率为1 000 Hz,电压为380 V时,连铸坯内部的电流分布如图4所示.对比图4(b)和(c)可知,二者的电流分布,以及电流密度、温度等物理量分布均相同,因此后续纵截面均选择平行于电流输入面的纵截面.

图4 连铸坯内部的电流密度分布Fig.4 Distributions of current density in the continuous casting billet

当连铸坯移动速度为1.2 m/min,激励电流频率为1 000 Hz,电压为380 V时,连铸坯纵截面的电流密度随加热时间的变化规律如图5所示.可知,随着加热时间的增加,连铸坯内部的电流密度幅值逐渐增加.

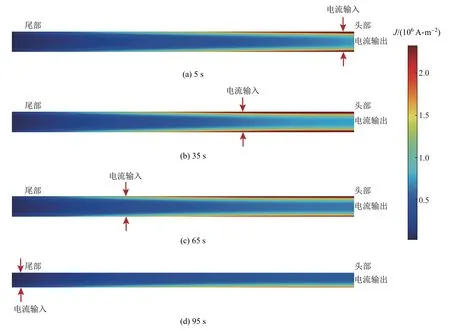
图5 连铸坯纵截面电流密度随加热时间的变化Fig.5 Variations of current density on longitudinal section of the continuous casting billet with heating time

为了更加清晰地展现电流在连铸坯长度方向上的分布规律,取连铸坯运动50 s(相应的运动距离为1 000 mm)后其纵截面中心线上不同位置的电流密度作图,结果如图6所示.可知:电流密度随着与连铸坯头部距离的增大而减小;连铸坯头部的电流密度最大,为3.2×106A/m2;;连铸坯尾部由于未接入电流,因此无电流通过.

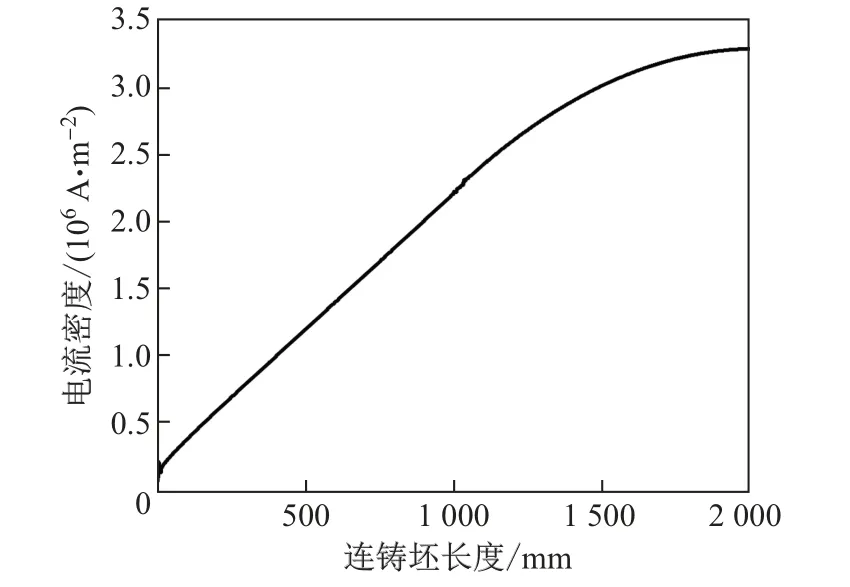
图6 连铸坯纵截面中心线的电流密度分布Fig.6 Distribution of current density on longitudinal section centerline of the continuous casting billet

当连铸坯运动40 s后,其不同位置横截面的电流密度分布如图7所示.可知:不同位置横截面芯部的电流密度差异较小,而角部的差异明显;电流主要集中于连铸坯角部;随着横截面与连铸坯端面距离的增大,横截面角部的电流密度显著减小.

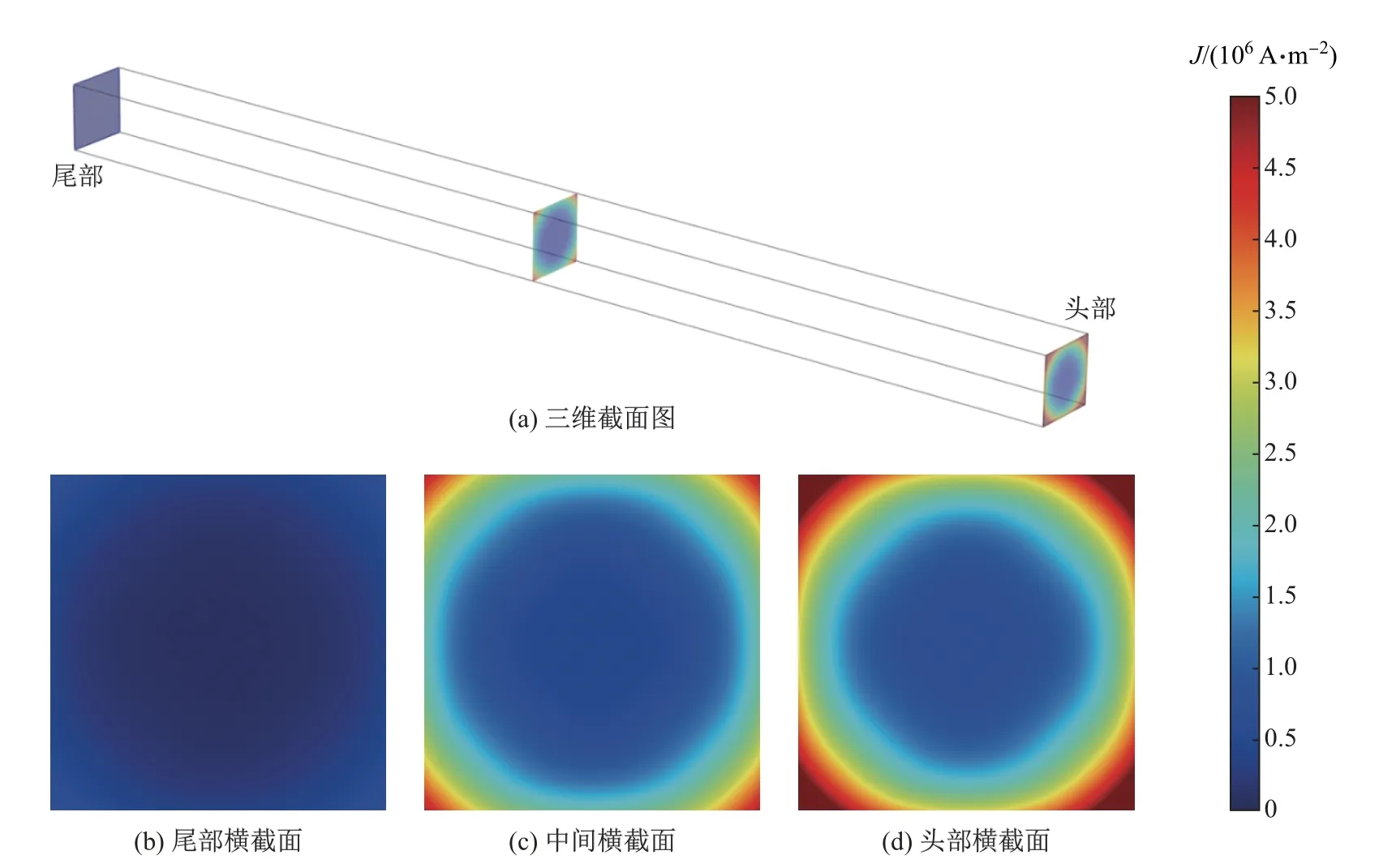
图7 连铸坯内部不同位置横截面电流密度分布Fig.7 Distributions of current density on different horizontal section of the continuous casting billet

为了定量分析横截面上的电流分布,取连铸坯端面芯部至表面中心的电流密度作图,结果如图8所示.可知:电流密度随着与连铸坯表面距离的增大而减小;连铸坯表面中心的电流密度最大,为3.25×106A/m2;连铸坯芯部的电流密度最小,为0.7×106A/m2.

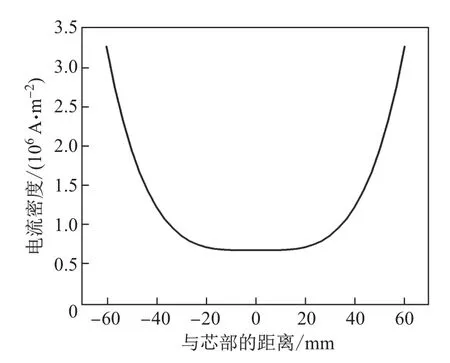
图8 连铸坯端面芯部至表面中心的电流密度变化Fig.8 Variation of current density from core to center of the surface at the top of the continuous casting billet

在电流作用下,连铸坯内部产生焦耳热.为了研究连铸坯内部焦耳热的分布规律,取连铸坯运动1 000 mm后其纵截面和横截面的焦耳热分布,结果如图9所示.可知:沿连铸坯长度方向,焦耳热集中于连铸坯头部;沿连铸坯径向,焦耳热主要集中于连铸坯表面.上述现象有利于降低连铸坯头尾温差和径向温差.

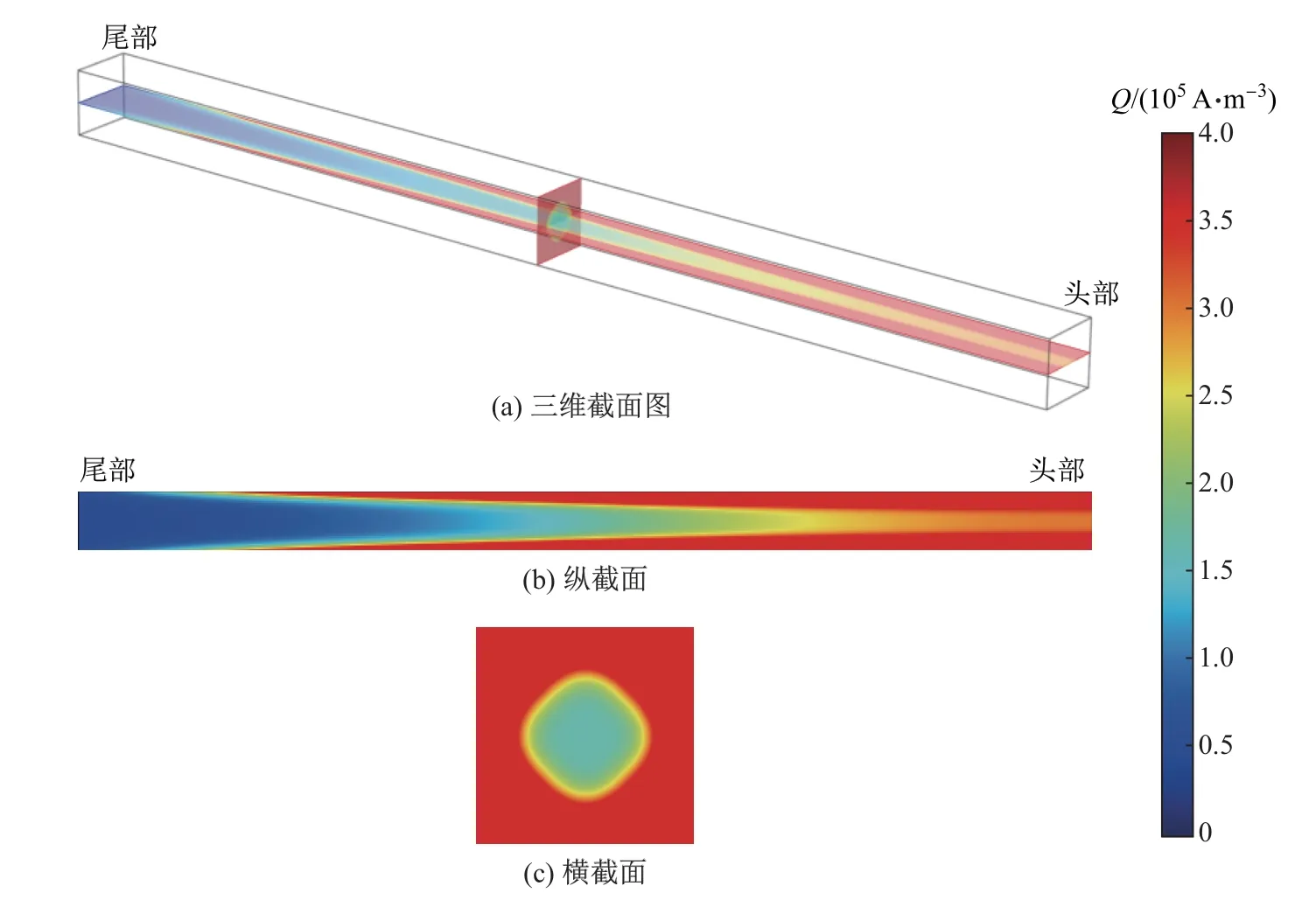
图9 连铸坯内部的焦耳热分布图Fig.9 Joule heat distributions in the continuous casting billet

3.1.2 温度场分布规律

图10(a)为连铸坯自然冷却100 s后,其水平截面(z=1 000 mm)的温度分布.图10(b)为经过交流电(380 V,1 000 Hz)加热100 s后,其水平截面(z=1 000 mm)的温度分布.对比图10(a)和(b)发现,经过电流加热,连铸坯水平截面的整体温度升高,同时径向温度梯度明显降低.

图10 连铸坯水平中间横截面的温度分布Fig.10 Distributions of temperature on the horizontal middle section of the continuous casting billet

为进一步研究电流加热对连铸坯温度的影响,取连铸坯水平截面(z=1 000 mm)芯部至表面中心的温度作图,并对比了初始时刻、自然冷却100 s和电流加热100 s后连铸坯的温度曲线,结果如图11所示.可知:相较于初始时刻,自然冷却后的连铸坯芯部与边部的温差由120◦C降低至77◦C;经过电流加热,连铸坯芯部与边部的温差进一步降低至60◦C;相较于自然冷却,电流加热能显著增加连铸坯边部的温度.

图11 连铸坯水平截面芯部至表面中心温度变化Fig.11 Variations of temperature from core to center of the surface at the horizontal section of the continuous casting billet

图12为自然冷却95 s与经过电流加热95 s后连铸坯纵截面的温度分布云图.可知,经过电流加热,连铸坯纵截面的温度分布更加均匀.同时,为了更加清晰地展现电流加热对连铸坯长度方向上温度的影响,对比了初始温度、自然冷却95 s与电流加热95 s后连铸坯中心不同高度的温度曲线,结果如图13所示.可知:自然冷却95 s后连铸坯头尾温差为80◦C;经电流加热后,连铸坯头尾温差降低至10◦C,同时整体温度高于1 173 K[18],满足了直轧工艺的最低温度要求.这些研究结果表明:基于电流加热的连铸恒温出坯方法能有效降低连铸坯首尾温差,实现了在长度方向上温度的均匀化;经电流加热的连铸坯头部温度高于尾部.这是因为连铸坯头部焦耳热集中(见图9),且头部受电流加热的时间多于尾部.

图12 连铸坯纵截面的温度分布Fig.12 Distributions of temperature at the longitudinal section of the continuous casting billet

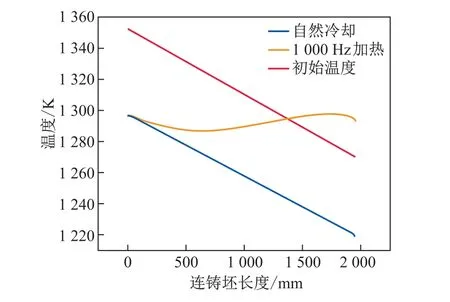
图13 不同条件下连铸坯表面轴线温度的变化Fig.13 Variations of surface axial temperature of the continuous casting billet under different conditions

3.2 激励电流频率对连铸坯温度场的影响

3.1节初步揭示了交流电对连铸坯内部电流和温度场分布的影响.研究结果表明,电流加热能在一定程度上降低连铸坯径向和长度方向的温度梯度.由于实际生产中激励电流参数和工艺参数都会影响电流的均温效果,因此还需讨论电流频率对连铸坯温度场的影响.

当恒定电压为380 V、连铸坯移动速度为1.2 m/min时,不同激励电流频率作用下连铸坯横截面(z=1 000 mm)芯部至表面中心的温度分布如图14所示.可知:随着激励电流频率的增大,连铸坯表面温度逐渐升高,芯部温度逐渐降低.产生上述现象的原因如下:随着激励电流频率的增大,电流的趋肤效应越发显著,因此电流对连铸坯表面的加热效果逐渐增强,从而导致温度上升;同时中高频条件下连铸坯芯部受焦耳热作用小,因此该区域热量持续向外部传递,最终呈现芯部温度随激励电流频率增大而降低的现象.值得注意的是,当激励电流频率增加至3 000 Hz及以上时,激励电流频率对连铸坯边部温度的提升并不明显.

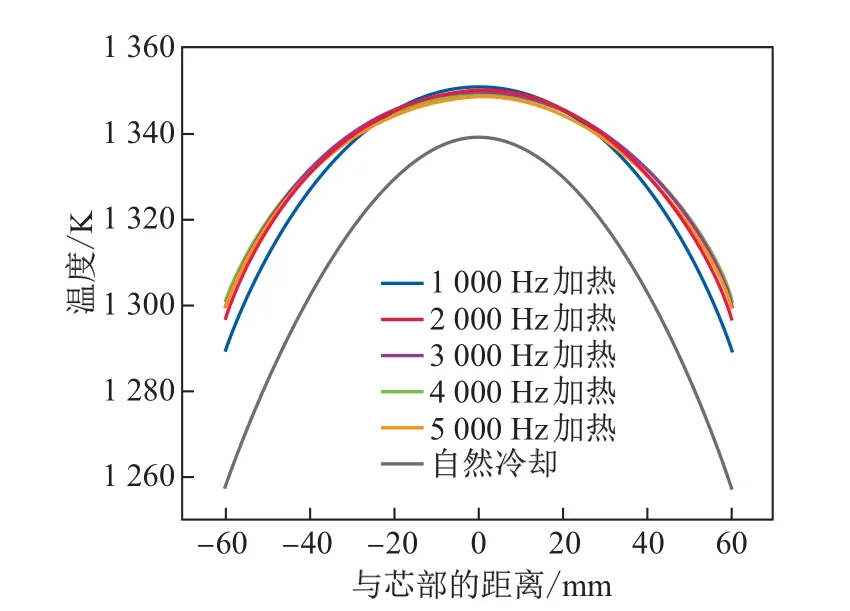
图14 不同激励电流频率作用下连铸坯横截面芯部至表面中心的温度变化Fig.14 Variations of temperature from core to center of the surface at the cross-section of the continuous casting billet under different current frequencies

当恒定电压为380 V、连铸坯移动速度为1.2 m/min时,连铸坯表面头尾温差随激励电流频率的演变规律如图15所示.可知:随着激励电流频率的增加,连铸坯头尾温差的绝对值先减少后增大;当激励电流频率为1 000 Hz时,头尾温差的绝对值最小,为7 K;当激励电流频率进一步增大时,连铸坯头部温度反而高于尾部温度.

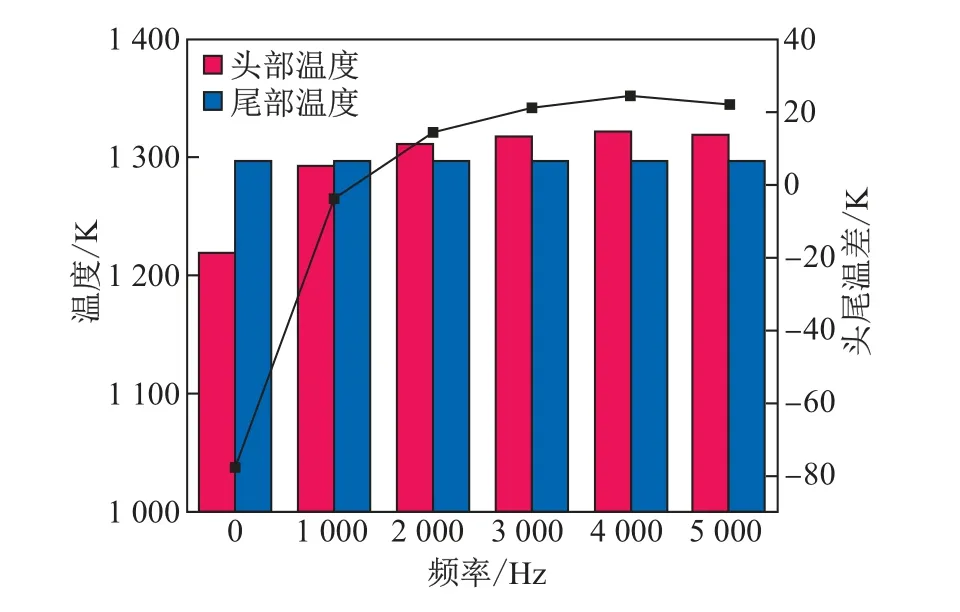
图15 不同激励电流频率作用下连铸坯的头尾温度Fig.15 Temperatures of the head and tail of the continuous casting billet under different current frequencies

为了进一步研究激励电流频率对连铸坯长度方向温度场的影响,取连铸坯表面中心不同位置的温度作图,结果如图16所示.可知:相比于自然冷却100 s的连铸坯温度,激励电流频率为1 000∼5 000 Hz条件下的电流能显著提升连铸坯长度方向的温度;随着激励电流频率的增大,电流对连铸坯头部温度的提升逐渐增强.考虑到4 000∼5 000 Hz条件下连铸坯长度方向的温度与3 000 Hz时较为接近,出于节能的考虑,在当前研究条件下选用频率为1 000∼3 000 Hz的交流电降低连铸坯头尾温差最为合理.

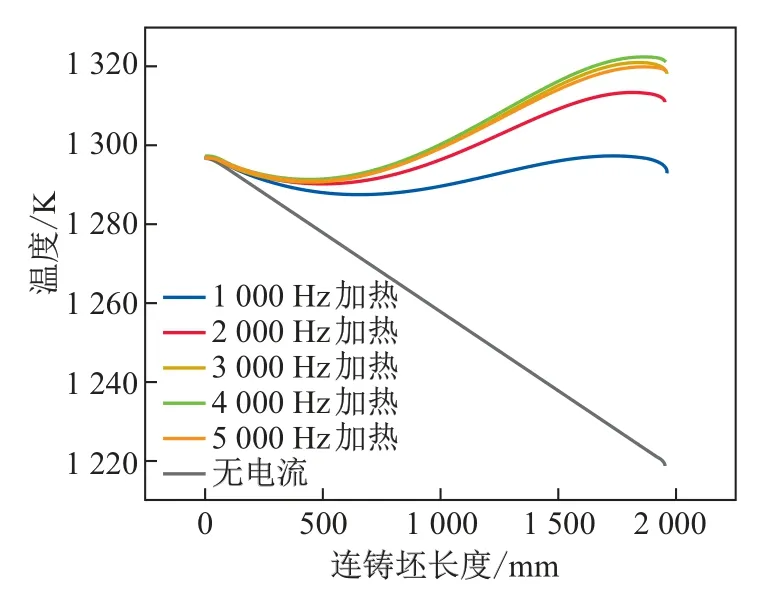
图16 不同激励电流频率作用下连铸坯表面温度的变化Fig.16 Variations of surface temperature of the continuous casting billet under different current frequencies

3.3 连铸坯移动速度对连铸坯温度场的影响

在恒定电流参数(380 V,3 000 Hz)条件下,连铸坯纵截面温度随其移动速度的演变规律如图17所示.当连铸坯的移动速度分别为1.2、2.1和3.0 m/min时,对应的电流加热时间分别为95、55和37 s.可知,当连铸坯移动速度增大时,连铸坯头部表面温度逐渐降低.这是因为随着连铸坯移动速度的增大,电流加热时间逐渐缩短,使得连铸坯头部的加热时间也相应减少.

图17 不同移动速度下连铸坯纵截面的温度分布Fig.17 Distributions of temperature at the longitudinal section of the continuous casting billet under different moving speeds

为了进一步研究连铸坯温度场随连铸坯移动速度的演变规律,取电流加热后连铸坯表面不同高度的温度作图,结果如图18所示.可知:连铸坯头部温度随其移动速度的增大而降低,尾部温度随其移动速度的增大而升高;1.2 m/min移动速度下连铸坯头部温度高于尾部温度,而其他移动速度下头部温度低于尾部温度.这是因为在高移动速度条件下,连铸坯整体受到的电流加热时间短,头部温度未能得到显著提升;当加热结束时,尾部降温时间短,残余温度较高.对比不同移动速度下连铸坯的头尾温差时发现,当连铸坯移动速度为2.1 m/min时,其头尾温差最小,为22◦C;连铸坯内部(720∼1 700 mm)温度相对更均匀.因此,在所选的移动速度范围内,2.1 m/min移动速度的均温效果最好.

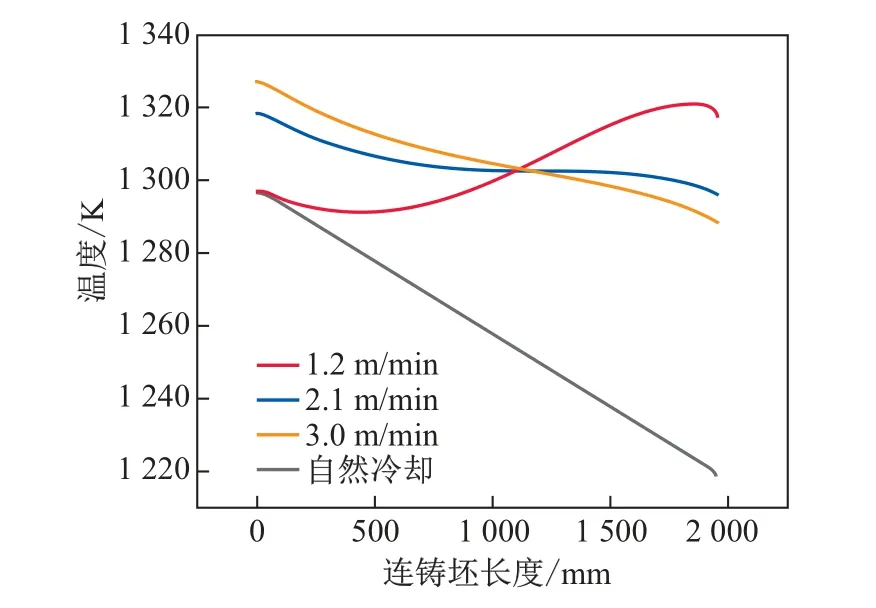
图18 不同移动速度下连铸坯表面轴线温度的变化Fig.18 Variations of surface axial line temperature of the continuous casting billet under different moving speeds

4 电流加热功率计算模型

本工作通过数值模拟,揭示了电流加热过程中连铸坯内部电流与温度场的分布及变化规律,以及连铸坯温度随激励电流频率和连铸坯移动速度的演变规律.然而在实际生产中,电流对连铸坯的均温效果受诸多因素影响,例如连铸坯的尺寸、物性参数、初始温度等.因此,需要根据实际工况设定合理的加热功率,从而实现不同工况条件下的连铸恒温出坯.

假设连铸坯温度沿长度方向线性分布,由于连铸坯温度随着与尾部距离的增大而降低,因此连铸坯沿长度方向的温度可表示为

式中:T1为连铸坯头部平均温度(K);T2为连铸坯尾部平均温度(K);x为到连铸坯尾部的距离(mm).

假设经过电流加热后,连铸坯整体温度均匀分布,设为T3.因此,电流作用下连铸坯由初始温度改变为目标温度T3的这一过程,可以等效为先将低于连铸坯尾部平均温度T2的部分加热至T2,再将连铸坯整体降温至T3.

在连铸坯整体升温至T2的过程中,单位体积吸收热量为

式中:δQ1为单位体积吸收热量值(J);C为连铸坯比热容(J/(kg·K));ρ为连铸坯密度(kg/m3);S为连铸坯横截面集肤层面积(m2);L为连铸坯长度(m);δx为单位长度(m).于是,连铸坯整体升温至T2吸收的总热量为

连铸坯整体温度由T2降至T3放出的总热量为

在电流加热期间,电流产生的总焦耳热近似为

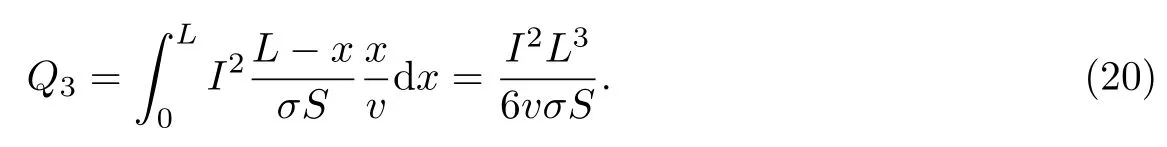
根据能量守恒定律可知:

将式(17)、(19)代入式(20),可得

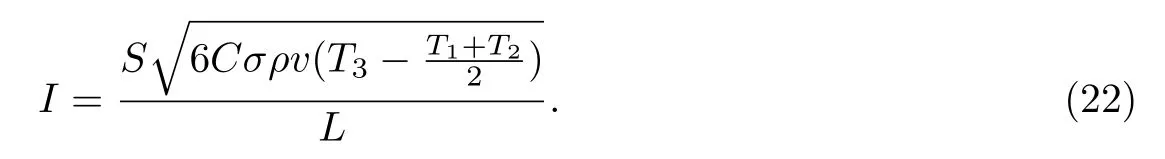
已有的电流加热功率表达式[19]为

式中:R为连铸坯电阻,其表达式为

S2为连铸坯横截面面积(m2).将式(21)、(23)代入式(22),得到了实现连铸恒温出坯所需的加热功率,即

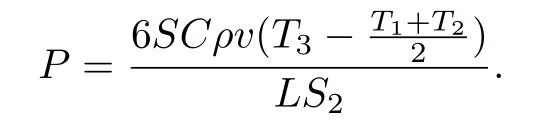
5 结束语

本工作提出了一种基于电流加热实现连铸恒温出坯的方法,通过数值模拟验证了该方法的可行性,并研究了激励电流频率和连铸坯移动速度对螺纹钢连铸坯温度场的影响.通过理论分析建立了电流加热功率计算模型,为确定实现连铸恒温出坯所需的加热功率提供理论依据.本工作得到了如下的主要结论.

(1)通过电流直接加热可以在降低连铸坯径向温度梯度的同时,降低长度方向的温度梯度.

(2)电流加热过程中,电流主要集中于连铸坯表面,电流产生的焦耳热由连铸坯表面向芯部衰减、由连铸坯头部向尾部衰减.

(3)激励电流频率与连铸坯移动速度对电流加热的均温化效果有显著影响,存在可实现最佳均温效果的频率和移动速度范围.

(4)建立电流加热功率理论计算模型.该模型可依据实际工况估算实现连铸恒温出坯所需的加热功率.