基于实时路径积分的双分子化学反应动力学计算方法

李永乐范文斌任伟

(1.上海大学理学院量子与分子结构国际中心,上海 200444;2.上海大学理学院上海市高温超导重点实验室,上海 200444)

化学反应速率常数的确定在燃烧[1-2]、星际分子[3]以及温室效应探索[4]的化学反应动力学建模中起决定性作用.基于确定同一反应、不同同位素的速率常数,计算得到动力学同位素效应(kinetic isotope effect,KIE),可以进一步研究化学反应中的量子效应(如量子隧穿(tunneling)和零点能(zero point energy,ZPE)等),以及动力学效应(如再穿越(recrossing)等).另外,理论计算得到的动力学同位素效应也反映了理论计算中使用的势能面的性质,从而帮助进一步优化势能面[5].其他化学反应动力学的相关物理量,如微正则系综速率常数[6]、反应几率[7]、散射截面[8]等,可以反映化学反应的动态信息,揭示反应的微观机理.由于化学动力学的实验测量通常是一件困难且昂贵的工作[9],而精确的理论计算可以做出可靠预测,其结果还直接对应一定的反应机理,故有助于促进实验技术的发展.因此,化学动力学的理论计算成为研究中不可或缺的重要手段[10-11].

目前,气相双分子反应动力学的理论计算为基于量子散射理论的含时波包动力学提供了较可靠的方法[12-13].结合高精度的神经网络(neural network,NN)势能面[14-15],其计算结果可以与当今量子态分辨高精度测量结果高度符合.如在最近工作中,Chen等[16]基于新开发的NN势能面上的波包动力学计算,并基于振动态分辨的反应几率和散射波函数分析,成功解释了杨学明院士团队在实验中观测到的Cl+CH4后向散射的微分截面在0.15 eV处的峰值,是来自于反应物的重-轻-重动力学效应而不是共振,是理论与实验紧密结合的研究典范.另外,目前已发表的文献表明,NN势能面已经能够拟合多达十个原子的反应体系[17],为计算复杂气相双分子反应提供了坚实基础.但是,基于高精度势能面的量子波包动力学方法,其计算量是根据原子数目呈指数级增长,目前仍不能满足反应动力学研究中对多原子反应的计算需求.在快速计算方面,过渡态理论(transition state theory,TST)[18]以及基于TST的各种改进方法[19-23]是最普通的选择.但TST计算忽略了量子力学的非定域性,以及反应中的动力学效应,导致TST结果存在较大误差,特别是低温下TST的计算结果与实验测量值往往相差若干数量级.另一种常用计算方法为准经典轨线法(quasi-classical trajectory,QCT)[24],该方法根据量子力学设置反应物的初态,用经典力学模拟散射过程,可以快速估算反应几率,并进一步求得散射截面、反应速率常数等物理量[11,25-27].不过,由于QCT的轨迹不包含量子效应,可能会发生零点能泄漏问题,也没有标准的指认产物态量子态分布的方法[28],故导致目前QCT只能作为研究反应动力学的辅助工具.

近年来,基于实时路径积分的珠串分子动力学(ring-polymer molecular dynamics,RPMD,珠串直译为环聚合物)[29-31]被广泛应用于各种气相双分子反应的热反应速率及KIE的计算中[32].RPMD提供了一套比TST和QCT更精确、比量子散射理论耗费资源更少的计算方案.即使在较低温度下的深度隧穿区域,RPMD也能给出足够精确的结果[33].虽然标准RPMD方法的计算量比基于波函数的量子力学方法小很多,但是受限于目前势能面计算能量的速度,目前RPMD可计算的系统仍然停留在七原子及以下反应,无法大幅超越量子波包动力学的应用范围,更无法达到TST和QCT广泛适用的要求.如果采用计算速度快但精度低的解析势能面,则即使应用RPMD也无法计算出正确的反应速率常数[34].目前,针对气相多原子分子反应动力学的理论研究仍然是化学动力学领域的前沿和难点之一[35],需要研究人员进一步完善计算方法.近年来,应用RPMD计算气相双分子化学反应的动力学又有了新的进展,该研究已经扩展到多通道化学反应、微正则系综速率常数、表面化学反应几率和反应截面的计算,本工作将对此进行综述.下面首先简述标准RPMD的化学速率常数计算方法,再简单介绍反应动力学理论的新进展与新应用.

1 方法

1.1 路径积分分子动力学

考虑一个质量为m的原子,引入P个串珠,有

式中:h为普朗克常数;p和q为串珠的经典动量和坐标;为系统哈密顿算符;βP的定义为

式中:kB为Boltzmam常数;HP是所谓的珠串哈密顿量,

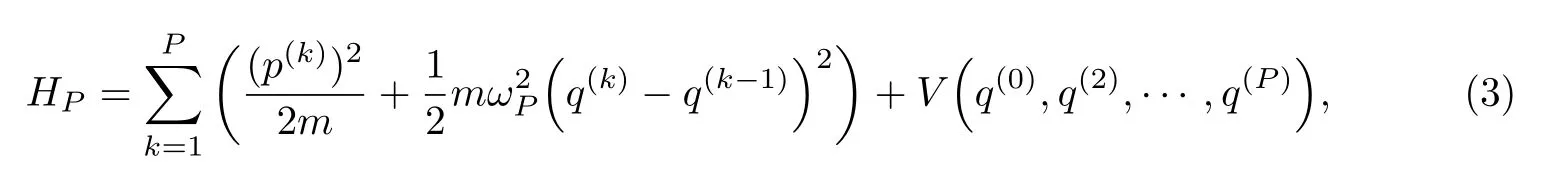
且珠串中珠子间首尾相连,有q(P)=q(0),连接相邻串珠的谐振子频率为

从化学反应的量子理论[36]

出发,计算得到热速率常数.式中:Qr为反应物的配分函数;cfs(t)为流关联函数,

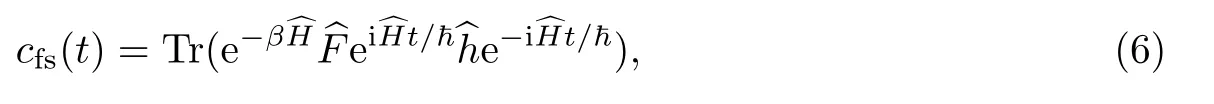
实际计算中,运用Bennet-Chandler分解[37],将计算归结为如下2个步骤.

步骤1计算自由能变.引入2个分隔面s0和s1,其中s0放在2个反应物相互作用可忽略的渐近区域内,s1放在过渡态区域内,由此定义出反应坐标ξ=s0/(s0−s1).再基于路径积分分子动力学(path-integral molecular dynamics,PIMD)沿着ξ的方向,运用增强采样(enhanced sampling)方法,计算出平均力势(potential of mean force,PMF)W(ξ),并确定其峰值对应的反应坐标ξ‡,计算得到

式中:R∞为设定的2个反应物相互作用可忽略的距离;µR为反应物的折合质量.

步骤2计算透射系数.在双dagger号ξ‡处进行基于RPMD的的计算:

式中:δ[ξ]为Dirac delta函数;h[ξ]为Heaviside阶跃函数.此处根据RPMD双分子反应速率理论的基本假设,认为RPMD中得到的对应了量子理论中的cfs(t).

最后,将这2个步骤的结果相乘得到最终速率.考虑到分子电子态的简并有时还需要乘以一项跟电子配分函数有关的修正系数f(T),于是得到

由于步骤2的计算可以模拟实时动力学,RPMD速率包含再穿越(recrossing)效应,可以消去人为引入分隔面带来的影响,因此分隔面的选取有一定的任意性,可在一定范围内任取[38].

2013年,Suleimanov等[39]开发了程序RPMDrate,用于计算气相中双分子化学反应速率常数.由于使用了Fortran和Python编程语言,故该程序得到了广泛应用.

在RPMD计算中,每个原子使用P个串珠(bead)来描述,这对计算量的需求呈线性增长.但由于标准RPMD方法中的时间步长通常为0.1 fs,而计算的轨迹需要数十纳秒(ns),且低温下往往需要多达数百个串珠来描述一个原子的运动,故导致计算效率又降低数百倍,难以满足相关研究的需求.以下将通过2个例子来说明.

OH+CH4在高温下的拔氢过程是天然气燃烧的重要反应步骤,而该反应在低温下是甲烷在大气层中消耗的关键反应步骤[40].刘国平院士课题组于2005年对OH+CH4展开了系列研究工作,系统测量了该反应的化学动力学,如产物之间的振动量子态的关联[41]及KIE[42]等.2018年,Li等[40]开发了基于置换不变多项式神经网络(permutationally invariant polynomial-NN,PIP-NN)的高精度全维势能面.基于此PIP-NN势能面,该课题组于2018年运用TST和QCT计算了OH+CH4的速率常数及OH/OD+CH4、OH+CH4/CD4、OH+12CH4/13CH4这3组KIE.结果表明,即使基于高精度势能面,TST和QCT的估算结果也仅仅在高温区可以与实验结果符合,而在低于300 K的低温区则存在较大误差.其他课题组针对该体系的工作,大部分也是基于高精度电子结构的计算结果运用TST或QCT,或者基于低精度的解析势能面运用高精度的动力学方法进行计算,如RPMD[43].上述二者都因为引入了误差更大的计算方法,所以得到的计算结果与实验数据偏离更大.

H+C3H8是燃料燃烧研究中重要的典型反应.早在1992年就有了关于该反应的量子态分辨的动力学研究[44].2017年的反应动力学实验已经可以精确测量不同反应通道的速率常数[45],这给理论计算带来了极大挑战,对于该反应目前还没有RPMD的计算结果.最近,Laude等[23]在对H及其同位素Mu和C3H8反应的瞬子TST计算中,由于只考虑了势能面上反应路径附近的区域,以及缺乏对再穿越等动力学效应的计算,故得到的KIE比实验值小1 000倍,误差极大.

由上述2个例子可见,对于复杂气相双分子反应,必须基于高精度势能面且运用包含了必要的量子效应的动力学方法(如RPMD),才能计算得到准确的反应速率常数、KIE和反应截面等反应动力学中的关键物理量.要达到上述目标,首先必须解决标准RPMD方法计算速度慢的问题,其次必须解决标准RPMD方法本身存在的问题.例如,最近发现即使是采用足够多串珠(bead)的标准RPMD计算,也存在数值不稳定性和非遍历性的问题[46].

因此,开发RPMD计算的新方法必须确保其正确模拟量子效应的同时提高其计算效率,才能使RPMD被广泛应用.近年来,美国加州理工学院的Korol等[46-47]进行了初步的尝试,其提出的Cayley传播子方法保持了RPMD的保辛性、时间可逆性、强稳定性和遍历性,同时支持较大的时间步长.

1.2 运用Cayley传播子加速RPMD

原始的路径积分分子动力学中,体系从t时刻随时间演化到t+∆t的运动方程为

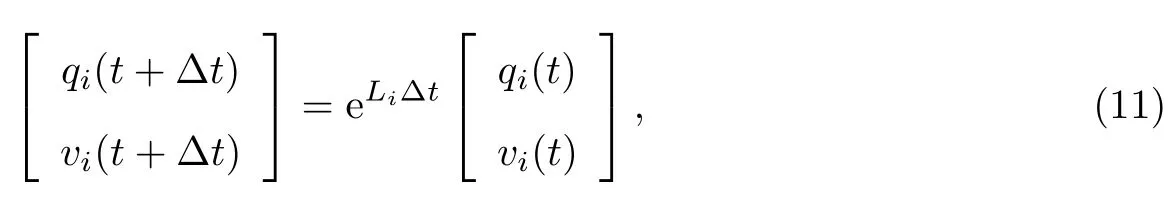
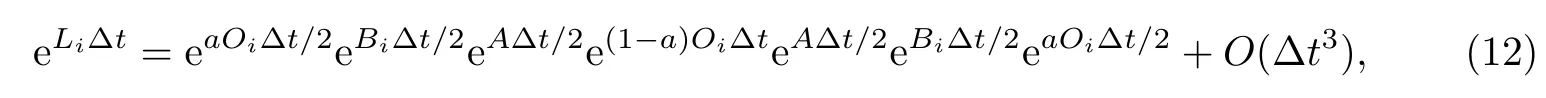
式中:A、B和O分别为自由珠串(free ring-polymer)随时间演化、在外加势能作用下随时间演化和控温;a为可调参数.这里,当a=1时,为标准的对称化RPMD时间演化方案OBABO;a=0时,时间演化记作BAOAB,即Liu等[48]和Zhang等[49]提出的中间控温方案(middle thermostat)具有一定的数值稳定性和计算效率优势.而O=0代表不控温,对应的是微正则系综中的时间演化.

上述传播子中,A具有精确解析表达式:

式中:ωP为串珠之间的谐振子频率,同式(4).

在数值计算中,需要引入近似RPMD传播子M(∆t)来计算exp(A∆t).这里M(∆t)需要满足3个条件:

(2)强稳定性:对所有的ωj,P>0,且∆t小于某不依赖于ωj,P的常数,M(∆t)都是强稳定的辛矩阵;

(3)时间反演对称性:对于速度反演矩阵

满足

标准的M(∆t)使用Verlet积分方法,即

此传播子不满足条件(2),导致标准的RPMD轨迹计算缺乏稳定性.而Cayley传播子考虑了随机时间步长δt,并对其取统计平均:

再将其对称化,得到A∆t的Cayley变换:

这个传播子可满足全部的上述3条性质.Cayley传播子方法就是利用上述cay(A∆t)来代替标准的RPMD传播子exp(A∆t)进行计算,类比上述A、B的记号,记作C.

考虑北京大学Liu等[48]提出的具有较高效率中间控温方案(记作BAOAB),即将自由珠串含时演化拆分成2个部分,在这2个部分中间进行控温,故Cayley传播子可以进一步写成相等的2个部分的乘积:

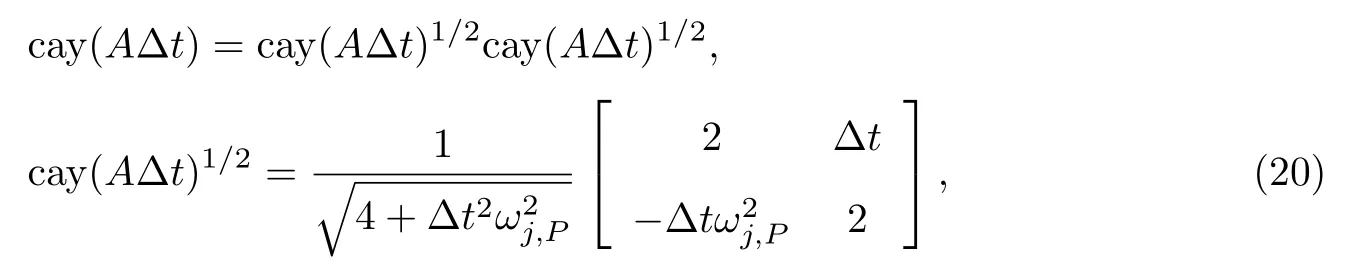
并在上述2个半Cayley传播子中间加入控温步骤,实现正则系综的Cayley传播子PIMD/RPMD模拟,记为BCOCB.这是目前已知数值稳定性最好的正则系综Cayley传播子实现方案[50].

现在,Cayley传播子可以对所有的串珠间谐振子频率给出正确的量子分布,且在传播中可以选取较大的时间步长[50-51].该方法目前已经在一维非谐振子、液相水振动光谱计算中获得了成功应用.目前,Cayley传播子已经编写进原有的RPMD计算程序,在H+H2中进行了测试,结果如表1所示.由表1可见,应用Cayley传播子后可以通过增大积分的时间步长,将计算速度提高了至少5倍而不改变计算结果.

表1 Cayley传播子RPMD(BCOCB)和标准RPMD(BAB+O)计算H+H2在300 K的速率结果对比Table 1 Comparion results of Cayley propogation sub-RPMD(BCOCB)and standard RPMD(BAB+O)calculated H+H2 at the rate of 300 K

1.3 RPMD微正则系综速率常数计算

通过基于RPMD计算出的不同温度下的大量热反应速率常数,应用最近开发的最大熵方法[53]可以计算得到微正则系综速率常数.由统计力学可知,热速率常数k(β)和微正则系综速率常数N(E)具有如下关系:

式中:β=(kBT)−1.运用Laplace逆变换,有

式中:

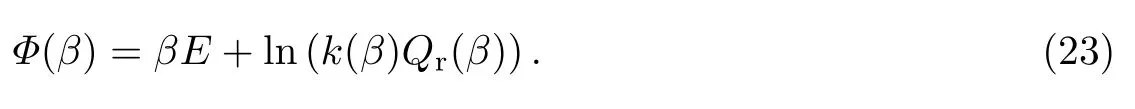
直接应用上述公式会有较大的统计误差,而应用最大熵方法可以得到有效的精确结果,因为计算是基于离散的数据点进行的.

首先,将热速率常数和微正则系综速率常数的关系式改写为矩阵形式:

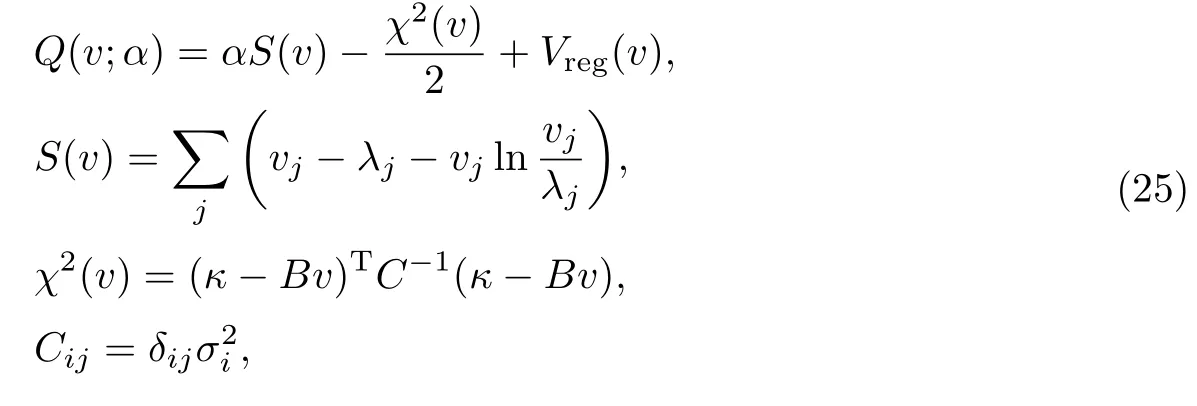
式中:S(v)为求得的v矩阵和某个模型λ(Ej)之间的信息熵;χ2(v)为似然函数;Vreg(v)为一个约束函数,用来保证N(Ei)∈[0,1],

式中:ζ为一个可调参数,通过测试计算确定.目前这套最大熵估计微正则系综速率常数的方法在一维模型体系中得到了验证,但尚未推广到双分子反应的计算中.而且,要得到微正则系综速率常数,必须首先获得至少数十个不同温度下的k(T).标准RPMD的耗时十分巨大,限制了基于RPMD的微正则系综速率常数的计算.但是,如果能成功提高RPMD计算效率,则双分子反应的微正则系综速率常数的计算也能得以广泛应用.

1.4 应用非平衡RPMD计算反应几率和反应截面

QCT方法计算双分子碰撞过程的计算量比标准RPMD更小,且相关物理量的计算较为简单直接,因此将RPMD与QCT结合将会是一个计算效率较高的方法.近期研究结果表明,RPMD模拟不受零点能泄漏问题的影响[7,54-55],计算结果的准确率将远高于标准QCT.Welsch等[56]基于非平衡RPMD,将RPMD初步应用于QCT的相关计算,得到了与实验结果高度符合的H2+Cu(111)和D2O+Ni(111)的表面散射反应几率[7];Marjollet等[8,57]运用这种思路计算了的Mu/H/D/Cl/F+H2散射截面.这些研究结果表明,RPMD-QCT计算具有广泛应用前景.但是,标准RPMD在QCT计算中需要很小的时间步长(约0.01 fs)以保证能量守恒,计算效率较低;另外,目前还没有一套成熟的、基于RPMD的初态选取和产物态指认方案.上述2个问题导致了目前结合标准RPMD的QCT进展缓慢,而新型传播子RPMD由于其计算效率高、稳定性强,有望结合QCT发展新型计算方法,并快速获得复杂气相双分子的热速率常数和KIE等化学动力学中的关键物理量,扩大RPMD在分子反应动力学理论研究中的应用范围.

1.5 应用机器学习电子结构计算辅助RPMD计算

复杂气相双分子反应的势能面开发较为困难.首先,应用高精度量子化学方法计算大量高维空间的构型要耗费大量机时;其次,构型的选取和势能面的构建与完善也需要消耗大量时间.而基于RPMD-QCT,采用基于量子化学计算得到的梯度进行直接动力学计算,可以避免构建势能面.但是,气相双分子反应的直接动力学需要较为精确的量子化学计算结果,目前常见的计算速度较快的量子化学方法(如密度泛函理论)无法满足精度需求.近年来,机器学习电子结构领域取得了显著的进展,其中基于分子轨道的机器学习(molecular-orbital-based machine learning,MOB-ML)方法[58-59]可以在Hartree-Fock(H-F)的计算速度下,达到耦合簇(coupled cluster single double(triple),CCSD(T))的精度.目前,MOB-ML方法已经可以计算闭壳层、开壳层和金属配合物体系,且具有解析梯度[60],计算效率较高.可见,基于这套机器学习量子化学计算方法直接进行RPMD动力学模拟,可以扩大RPMD-QCT的应用范围.

2 结论

目前,国内外应用RPMD计算双分子化学反应速率的研究人员逐年增多,有大连化学物理研究所/复旦大学张东辉课题组、南京大学谢代前课题组、重庆大学李军课题组、西北工业大学孟庆勇课题组、塞浦路斯研究所Yury等.本课题组于2012年首次将RPMD应用于具有van der Waals势阱的重-轻-重气相双分子反应O+CH4的研究,获得了与高精度量子波包动力学一致的结果.此后,本课题组继续致力于RPMD方法在反应动力学中的推广,取得了一系列的成功,如计算无能垒反应O+H2的速率常数等[61].2017年,Zuo等[62]基于MPI4Py开发了跨节点并行的RPMD速率计算版本,应用于本课题组及重庆大学李军、南京大学谢代前课题组的研究中.2020年,本课题组还将RPMD的应用拓展到多通道漫游反应[63].

近年来,对RPMD直接发展的有加州理工学院Miller课题组和中科院北京化学研究所的史强研究员合作开发的非平衡RPMD、非绝热RPMD以及Cayley传播子RPM;瑞士洛桑联邦理工学院的Ceriotti开发了适合RPMD的新型控温方法;美国Stanford大学的Markland将RPMD应用于凝聚相体系;北京大学的刘剑课题组在RPMD的控温和非绝热动力学方面做了重要工作等.

综上所述,针对复杂气相双分子化学反应的反应速率常数、KIE和反应截面等反应动力学关键物理量的计算,实时路径积分RPMD方法体现了强大的应用价值.但是,现有的理论研究方法仍然存在明显不足.如何基于实时路径积分方法,快速且高精度地计算化学反应动力学中的速率常数等关键物理量,目前仍然是研究的热点.未来的发展可能包括如下几个方向:

(1)运用新型传播子加速标准的RPMD方法,使计算速度进一步加快;

(2)开发RPMD-QCT计算方案,使得对化学反应动力学关键物理量的计算不需要计算自由能,可以大大提高计算效率;

(3)结合机器学习量子化学计算方法的直接动力学,实现快速准确地计算上述物理量.

上述3个方向的理论进展,将会使研究人员对双分子气相化学反应的机理有更深层次的认识,也将扩大RPMD的应用范围,为双分子反应动力学研究中理论与实践结合提供更有力的理论计算工具.