几种哈密顿量的写法与变换

吴 超 王海艳

宜春学院物理科学与工程技术学院 江西宜春 336000

J-C模型是量子光学发展的基本模型，已经有近50年历史，正是J-C模型的建立，才让物质与光场相互作用的研究越来越清晰。它主要描述的是限制在光学腔中的单个电磁模和一个两能级原子的相互作用，能量则在场和原子间相互交换，从而可以直接导致相干布居振荡以及叠加态的产生。由于J-C模型精确可解，相关物理问题就研究更为透彻，比如研究量子纠缠、量子逻辑门、光力等问题。对于复杂系统而言，多能级原子与多模电磁场的相互作用研究显得更为重要，而将这些复杂系统的哈密顿量简化成J-C模型则是一项很重要的理论工作。

下文总结了物质与光相互作用系统的几种哈密顿量，并求解了其中一种较为复杂实际系统的有效哈密顿量，也概述了一些复杂实际系统是如何简化成J-C模型的有效哈密顿量。这对从事理论量子光学研究有一定参考价值[1-3]。

1 一个两能级原子与一个外加经典驱动场相互作用的哈密顿量

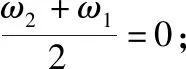
(1)

2 一个两能级原子与一个外加量子场相互作用的哈密顿量

(2)

3 一个三能级原子与两个外加经典驱动场相互作用的哈密顿量

根据理论量子光学理论，第一、第二和第三能级的频率为ω1、ω2、ω3，与第一个经典驱动场(频率为μ1)有关的拉比频率为Ω1，与第二个经典驱动场(频率为μ2)有关的拉比频率为Ω2，能够得到它的哈密顿量为：

H=ћω1|1〉〈1|+ћω2|2〉〈2|+ћω3|3〉〈3|+ћΩ1[|1〉〈2|e-iμ1t+|2〉〈1|eiμ1t]+ћΩ2[|2〉〈3|e-iμ2t+|3〉〈2|eiμ2t]

(3)

4 一个两能级原子与一个外加经典驱动场，两个外加量子场的相互作用的哈密顿量

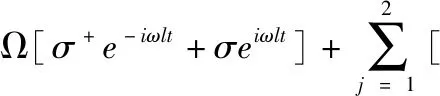
(4)

现在我们将这一复杂系统的哈密顿量进行推导，导出具有类J-C模型的有效哈密顿量。

首先我们将上式的哈密顿量分解成两部分：

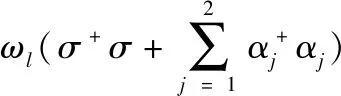
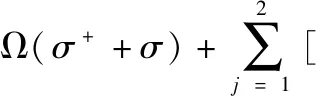
(5)

σ+=|e〉〈g|=cosθsinθπz+cos2θπ+-sin2θπ,σ=|g〉〈e|=cosθsinθπz-sinθπ++cos2θπ

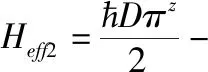
(6)

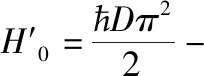
(7)

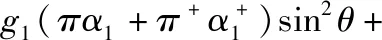
(8)

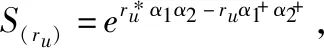
(9)

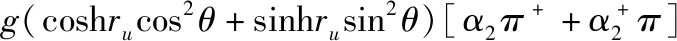
(10)

我们也可以得到以上类J-C模型的哈密顿量。

5 几种复杂实际系统简化后的J-C模型的哈密顿量

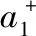
(11)

(12)

(13)

(14)

(15)

很明显，(12)、(13)、(14)、(15)式也是类J-C模型。

Case2：一个三能级原子与双模量子场相互作用，这双模量子场分别为一个为泵浦场，一个为斯托克斯模，|1〉，|2〉，|3〉分别代表原子的三个能级，该复杂系统总哈密顿量为[5]：

(16)

经过幺正变化得到有效哈密顿量为：

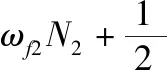
(17)

Case3：一个三能级原子与双模量子腔场相互作用，|1〉、|2〉、|3〉分别代表原子的三个能级，任何高能级与最低能级的跃迁由两个经典场Ω1和Ω2来驱动，失谐量为Δ，；两个量子腔模g1，g2分别耦合在能级|3〉⟺|2〉和|3〉⟺|1〉之间，失谐量为Δ。该复杂系统总哈密顿量为[6]：

(18)

(19)

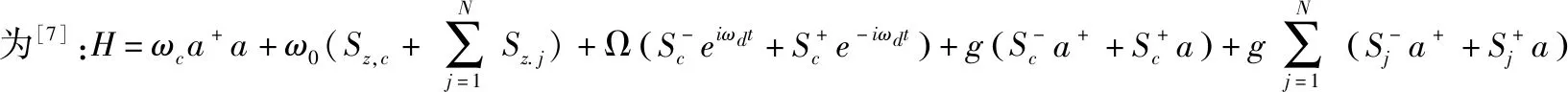
(20)

(21)

结语

在物质与光相互作用的研究中，由于模型变得越来越复杂，经常用到单个二能级原子或者多个二能级原子，有时又用到单个三能级原子或多个三能级原子，有时又研究N原子样本，甚至要考虑用经典场驱动原子跃迁。跃迁过程中有时是共振状态，有时又是失谐状态，严格点还考虑马尔可夫效应。所以初始的系统哈密顿量极其复杂，这就使得获得系统的有效哈密顿量变得很重要。本文给出了一点数学技巧和有效哈密顿量总结，这对更复杂系统优化成类似J-C模型的哈密顿量有参考价值。