Rn上的测度双K-框架

尚蒙娟, 朱玉灿

(福州大学数学与统计学院， 福建 福州 350108)

0 引言

Hilbert空间中的框架作为标准正交基的一种推广, 两者不同的关键在于空间中的元素用框架展开的表达式是不唯一的. 目前, 框架理论已广泛应用于各领域, 参见文献[1-3].

虽然框架重构表达式的形式看起来不复杂, 但计算量稍大.而紧框架比框架的重构表达式的形式更简洁, 计算更简单, 因此紧框架比框架应用领域更广泛.每个框架都可以延拓为紧框架.是否每个K-框架也可以延拓为紧K-框架? 答案是不行, 具体参见命题1.但是双K-框架却可以延拓为紧K-框架, 所以研究双K-框架很重要.类似地讨论双K-框架的推广, 即测度双K-框架.

在以上文献的基础上, 引入测度双K-框架的概念.由于双K-框架是近几年刚提出的, 因此对双K-框架性质的研究文献较少.本研究主要讨论双K-框架的一些性质, 研究任一个测度双K-框架可以膨胀为紧测度K-框架; 分析不同空间的测度双K-框架在算子扰动下的稳定性.

采用如下记号：H是一个可分的复Hilbert空间,I是H的恒等算子.设H1,H2是两个复Hilbert空间,B(H1,H2)表示从H1到H2的所有有界线性算子的集合.特别地,B(H)表示从H到H的所有有界线性算子的集合.若T∈(H1,H2), 则用R(T)和NT分别表示算子T的值域和核,Ω表示Rn的非空子集, B表示Ω上的Borelσ-代数, 其元素称为Borel集,M(Ω, B)为定义在B上的有限正测度集合.

1 预备知识

定义1[7]设μ∈M(Ω, B), 若存在正数α,β, 使得对于∀x∈Rn, 有：

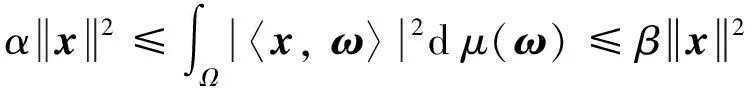
(1)

则称μ为Rn上的测度框架, 其中α,β分别为测度框架μ的下界、 上界.特别地,α的上确界和β的下确界分别成为测度K-框架的最佳下界和最佳上界.若只有式(1)右边不等式成立, 则称μ为Rn的Bessel测度.若α=β, 则称μ为Rn的紧测度框架.若α=β=1, 则称μ为Rn的Parseval测度框架.

对于Rn的Bessel测度μ∈M(Ω, B), 称有界线性算子θμ满足：

θμ:Rn→L2(Ω,μ),θμx=〈x, ·〉Rn

(2)

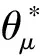
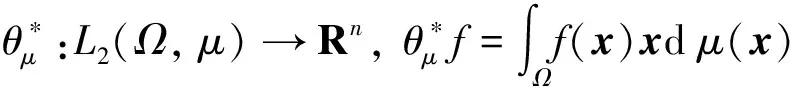
(3)

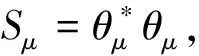
(4)

称Sμ为μ的框架算子.

定义2[14]设K∈B(Rn),μ∈M(Ω, B)称为Rn上的测度K-框架, 若存在正数α,β, 对于∀x∈Rn, 有：

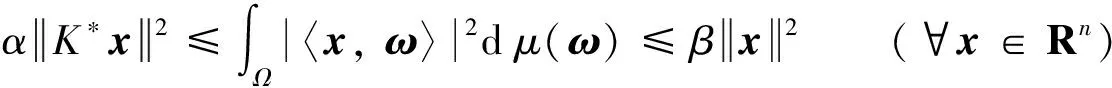
(5)

其中:α,β分别为测度K-框架μ的下界、 上界.特别地,α的上确界和β的下确界分别成为测度K-框架的最佳下界和最佳上界.

(6)

定义4[15]设K1∈B(H1),K2∈B(H2)， 若存在可逆的有界线性算子T:H2→H1满足：TK2T*=K1, 则称K1,K2关于算子T相似等价的.

定义5设K∈B(Rn), 称μ∈M(Ω, B)为Rn上的测度双K-框架, 若存在正数α,β, 使得

(7)

称α,β分别为测度双K-框架μ的下界、 上界.特别地,α的上确界和β的下确界分别称为测度双K-框架的最佳下界和最佳上界.若α=β, 则称μ为Rn的紧测度K-框架.

注1若K=I时, 则μ为Rn上的测度框架, 从而测度双K-框架可视为测度框架的一种推广.

2 一些引理

引理1[16]若T∈B(H)且T有闭值域, 则1)～3)成立.

1) 存在唯一的算子T+∈B(H)满足：

称T+为T的伪逆算子, 特别地, 如果T为可逆的有界线性算子, 则T+=T-1.

2)T+T=πR(T+),TT+=πR(T)， 其中πR(T+)和πR(T)分别是从H到R(T+)和R(T)上的正交投影.

3)R(T*)是H的一个闭子空间, (T*)+=(T+)*.

引理2[17]若T∈B(H), 则Ⅰ)～Ⅲ)成立.

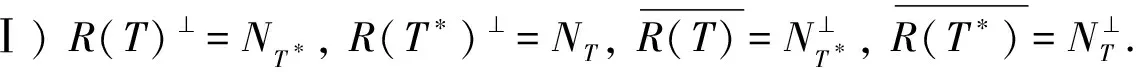
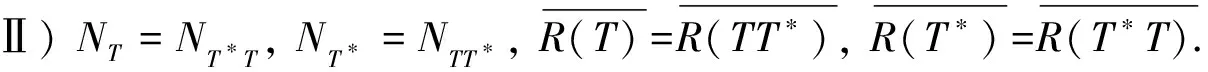
Ⅲ) 如果H的四个子空间R(T),R(T*),R(TT*),R(T*T)中有一个是闭子空间, 则其他三个也是闭子空间.

3 测度双K-框架

下面讨论利用测度K-框架来构造R(K)上的测度双K-框架.

定理1设μ∈M(Ω, B)是Rn的测度K-框架,K∈B(Rn), 则μ∈M(Ω, B)是R(K)的测度双K-框架.

证明 因为μ∈M(Ω, B)是Rn的测度K-框架, 所以

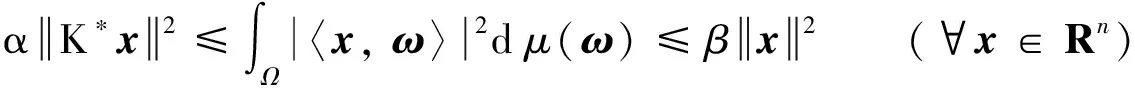
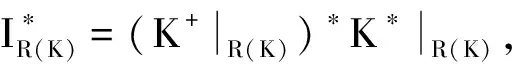
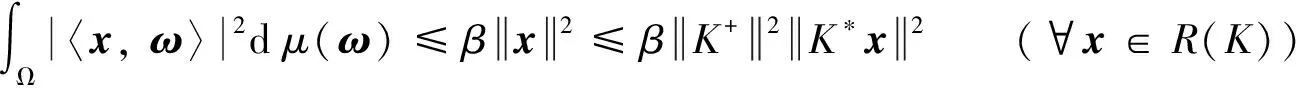
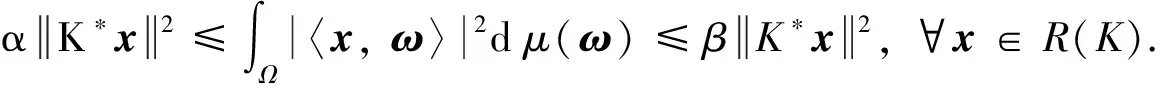
命题1设μ∈M(Ω, B)是Rn的界为0<α≤β<∞的测度K-框架, 如果存在Rn的Bessel测度ν∈M(Ω, B), 使得μ+ν∈M(Ω, B)是Rn的界为λ的紧测度K-框架, 则μ∈M(Ω, B)是Rn的测度双K-框架.

证明 如果存在Rn的Bessel测度ν∈M(Ω, B), 使得μ+ν∈M(Ω, B)是Rn的界为λ的紧测度K-框架, 即:

则:

又因为μ∈M(Ω, B)是Rn的测度K-框架, 所以下式成立.

故μ∈M(Ω, B)是Rn的测度双K-框架.

由测度框架的若干性质知, 在一定条件下, 任给一个测度框架添加测度框架后使之成为紧测度框架[8].由命题1知, 测度K-框架膨胀为紧测度K-框架, 只能是测度双K-框架, 类似于测度框架提升的证明, 可以得到测度双K-框架可以向紧测度K-框架的膨胀.

定理2设μ∈M(Ω, B)是Rn的界为0<α≤β<∞的测度双K-框架, 则存在Bessel测度ν∈M(Ω, B), 使得μ+ν∈M(Ω, B)是Rn的界为λ的紧测度K-框架, 其中λ>β.

证明 设μ∈M(Ω, B)是Rn的测度双K-框架, 其框架算子为Sμ， 则存在正数α,β, 使得：

从而对任意x∈Rn， 有：

故存在Bessel测度ν∈M(Ω, B), 使得μ+ν∈M(Ω, B)是Rn的界为λ的紧测度K-框架.

先考虑两个相似等价算子K1,K2所刻画的测度双K1-框架和测度双K2-框架之间的关系.

定理3设K1∈B(Rn),K2∈B(Rn)是关于可逆的有界线性算子T:Rn→Rn相似等价的,μ∈M(TΩ,TB)是Rn的测度双K1-框架.则ν=μ∘T∈M(Ω, B)是Rn的测度双K2-框架.

证明 由于μ∈M(TΩ,TB)是Rn的测度双K1-框架， 则：

令ν=μ∘T∈M(Ω, B), 于是对任意y∈Rn， 有：

即对任意y∈Rn， 有：

又对任意y∈Rn， 有：

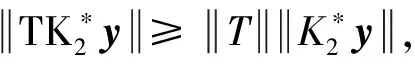
从而

故ν=μ∘T∈M(Ω, B)是Rn的测度双K2-框架.

进一步讨论， 不同空间的测度双K-框架在有界线性算子扰动下的稳定性.

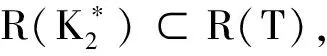
证明 设μ∈M(T+Ω,T+B)是Rn的测度双K1-框架, 则：

又T∈B(Rn,Rm), 且Rm是有限维空间, 所以R(T)是闭的, 由引理1得到T的伪逆算子T+存在, 且TT+|R(T)=IR(T).由Ω⊂R(T), 据引理1得：TT+Ω=Ω.对每个ω∈Ω， 令z=T+(ω), 则Tz=TT+ω=ω,ω∈Ω.所以对任意x∈Rm， 有：

从而对任意x∈Rm， 有：

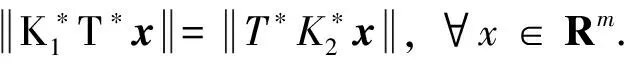
从而

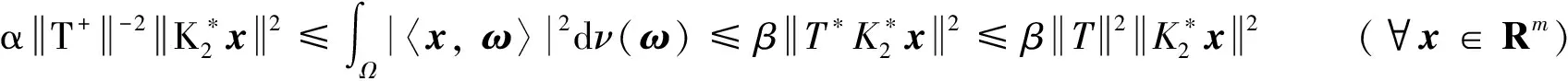
故ν=μ∘T+∈M(Ω, B)是Rm的测度双K2-框架.