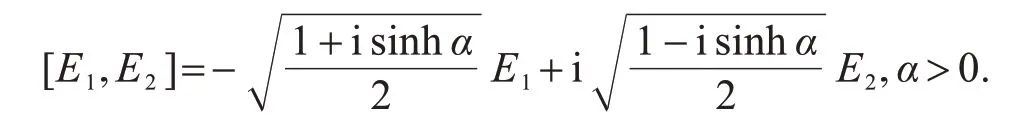三维时空中一对复主曲率类时共形齐性曲面的分类

林燕斌

（闽南师范大学数学与统计学院,福建漳州 363000）

1995年，Wang王长平[1]研究了x:M3→S4是具有三个不同实主曲率{λ1,λ2,λ3}的浸入超曲面x(M3)，定义超曲面的Möbius不变曲率W,同时给出了如下基本定理.

定理1{θ1,θ2,θ3;W}是超曲面M3的一个完备Möbius不变量系统.

进而他证明了这一类Möbius齐性超曲面是常Möbius曲率的杜邦超曲面，并且Möbius等价于下面情况之一：一个是S3中平坦环面在R4中做锥，另一个是S4中三个不同主曲率的等参超曲面.

1998 年,Wang[2]定义了无脐点浸入子流形x:Mm→Sn的4 个Möbius 不变量分别为：Möbius 度量g，Möbius形式Φ，Blaschke张量A 和Möbius第二基本形式B，并建立了子流形的一个完备的不变量系统.随后李同柱等[3-4]给出了Sn+1中具有两个和三个不同主曲率的Möbius齐性超曲面的分类定理，并且证明了这类超曲面除了对数螺线柱面外，都是常Möbius曲率的杜邦超曲面.

1 类时曲面的不变量系统

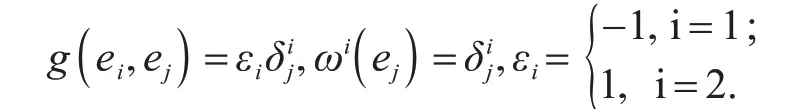
在活动标架{ei,n}下x的结构方程为：

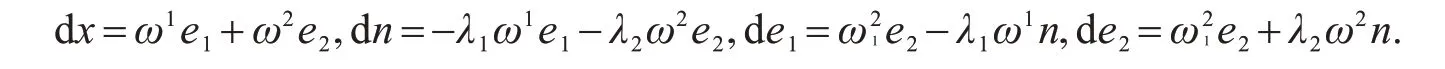
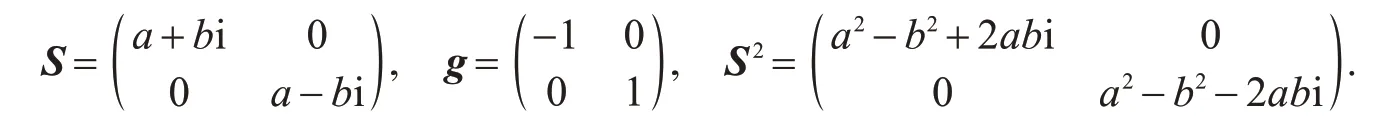
因此，tr(S)=2a,tr(S2)=2(a2-b2),则曲面x的Laplace算子为Δx=tr(S)n=2an.

定理2设中具有一对复主曲率{λ1,λ2}的连通正则曲面,定义下面形式：

1)标准共形不变度量gc:=b2g.

2)共形不变曲率W:=1.

3)典则提升Y:=by,其中.

5)典则法标架ξ:=ay+ξn,其中.

令ηi=Ei(Y),则沿着定义了的一组活动标架为,其中是由=0唯一决定的向量且与其它标架正交.

利用待定系数法,可以求得曲面在共形标架下的结构方程为

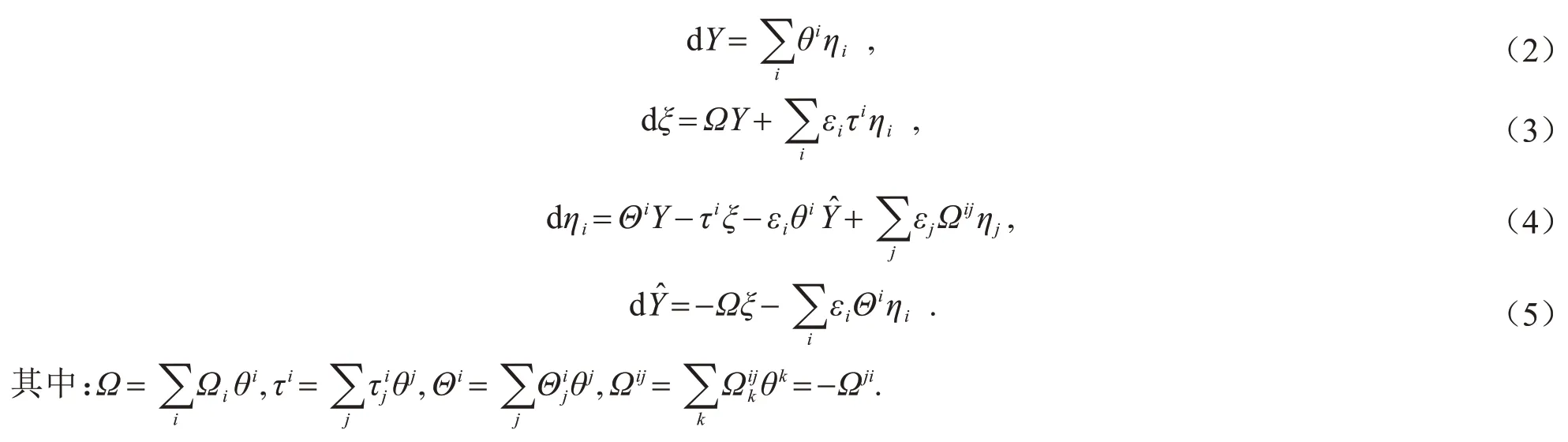
通过观察结构方程，可得如下定理：

定理3如果中具有一对复主曲率的两个曲面,若它们有相同的联络形式，Blaschke 张量,共形形式和共形第二基本形式,则存在共形变换T∈O(3,2)使得它们全等.

根据Poincaré引理，也可以求得曲面的可积条件为

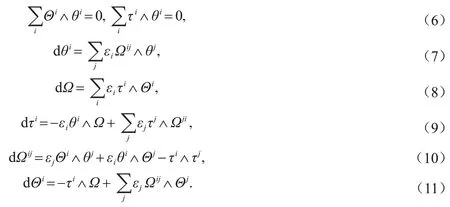
因此，得到如下重要定理.

定理4{E1,E2}是具有一对复主曲率的曲面的一个完备共形不变量系统.

证明根据方程(9)得到

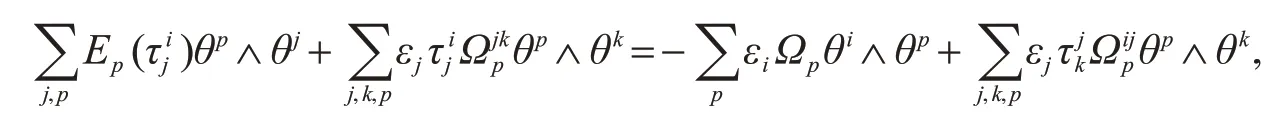
对比θi∧θj项的系数可知，,

由此说明,共形形式Ω由Ei,Γ和Ωij决定.

根据方程(8)推出,对比θi∧θj项的系数可得

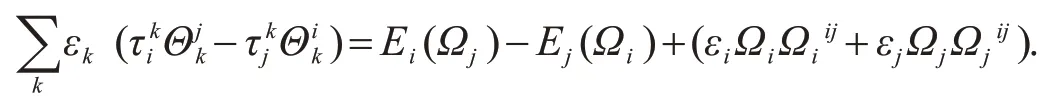
根据方程(10)推出

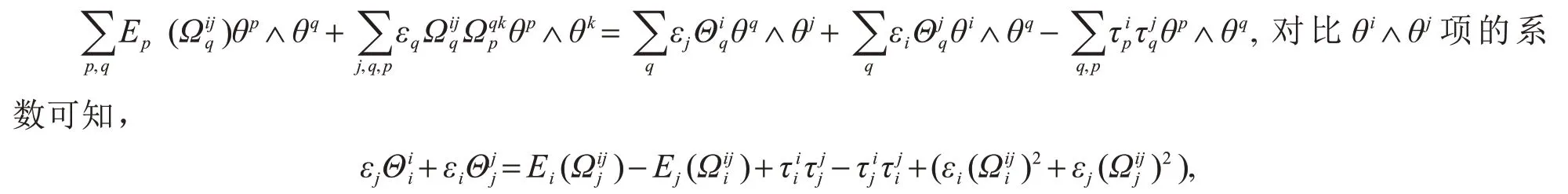
由此说明Blaschke张量Θ由Ei,Γ和Ωij决定.

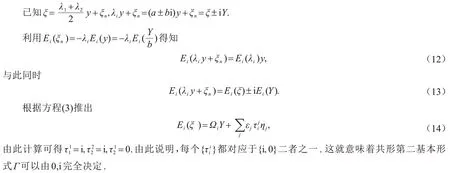
因此,该类曲面的李括号为

这就说明联络形式Ω12可以由[E1,E2]完全决定.

综上所述,我们发现共形形式Ω，Blaschke 张量Θ,共形第二基本形式Γ和联络形式Ωij,可由0,i和李括号[E1,E2]完全决定.

注1利用定理4,我们最终通过计算李括号[Ei,Ej]是否相等,从而快速判断两个类时曲面是否全等.故只需要计算曲面的主曲率{λi}和主方向{ei},然后就可以算得李括号[Ei,Ej].如果两个曲面的[Ei,Ej]相同,则它们在允许相差一个共形变换下两个曲面是全等的.

2 类时共形齐性曲面的分类结果

本节研究的是形状算子可对角化且有一对复主曲率的类时共形齐性曲面.若连通正则共形齐性曲面具有两个共形不变切标架，则此时沿着定义的一组共形标架是唯一确定的.此时，标架是唯一确定的共形不变标架且所有的不变量都是常数.

下面给出共形齐性曲面和类时杜邦曲面的定义:

定义1如果对任意两个点p,q∈,都存在中一个共形变换σ使得σ(x(p))=x(q),,则称为共形齐性曲面.

定义2如果主曲率沿着相应的曲率面为常数,则称是类时杜邦曲面.

在此首先给出如下定理:

定理5如果是常共形曲率曲面,则它是类时杜邦曲面当且仅当Ω=0.

证明利用方程(12),(13),(14),则容易证明该定理成立.

最后,可以得到重要的分类定理:

定理6设是形状算子可对角化且有一对复主曲率的类时共形齐性曲面,则该类曲面共形等价于类时杜邦曲面或者洛伦兹平面上的对数曲线,见如下例1.

证明在下面的证明过程中分两种情形进行讨论.

情形1若在共形齐性曲面中Ω=0,根据定理5可知，该类曲面共形等价于类时杜邦曲面.

情形2接下来，我们只讨论非杜邦的曲面，即Ω≠0的情形.根据方程(14)，此时共形第二基本形式Γ的系数是唯一确定的，即.

根据方程(6)和(8)比较θ1∧θ2项的系数可得,.

根据结构方程求得这类曲面对应的李括号为

由方程(7)和(9)比较θ1∧θ2项的系数得出，.

再由方程(10)比较θ1∧θ2项的系数得出

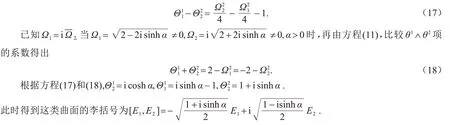
根据定理4可知，该类曲面共形等价于洛伦兹平面上的对数曲线，见如下例1.

综上所述，定理6证毕.

在齐性条件下，利用求解微分方程的方法，对结构方程和可积条件进行计算，可以构造出如下共形齐性非杜邦曲面的实例.

例1假设中具有基{ui},对于任给的常数α＞0,存在共形变换子群

因为S(ψ,φ)◦[gij]◦ST(ψ,φ)=[gij],S(ψ,φ)∈O(3,2),S(ψ1,φ1)◦S(ψ2,φ2)=S(ψ1+ψ2,φ1+).所以矩阵S(ψ,φ)是O(3,2)的子群.选取类光向量P=使得

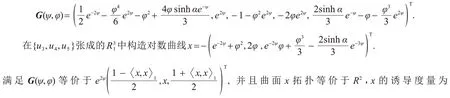
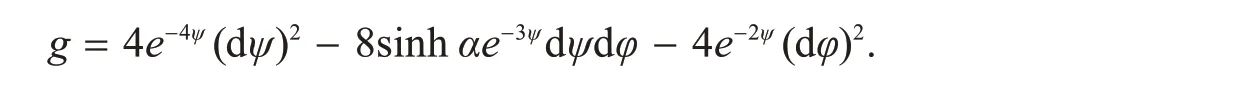
x的单位法向量为

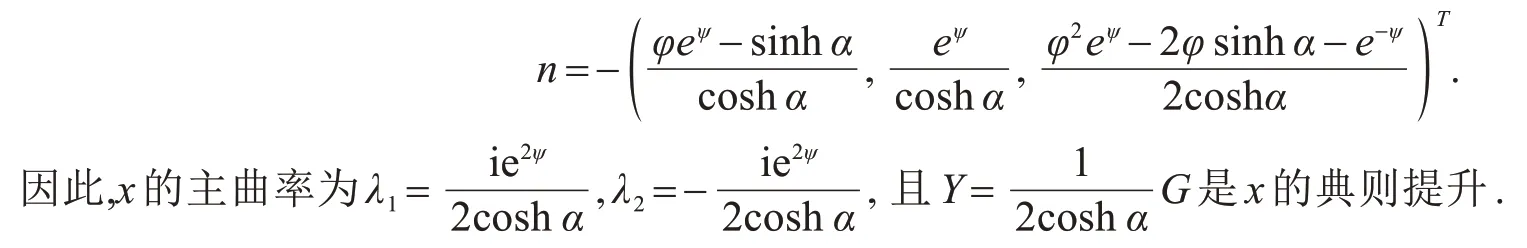
Y的标准共形不变度量为

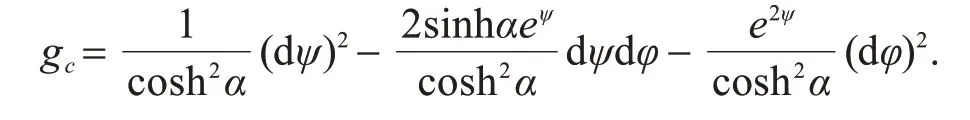
我们选择共形切标架为

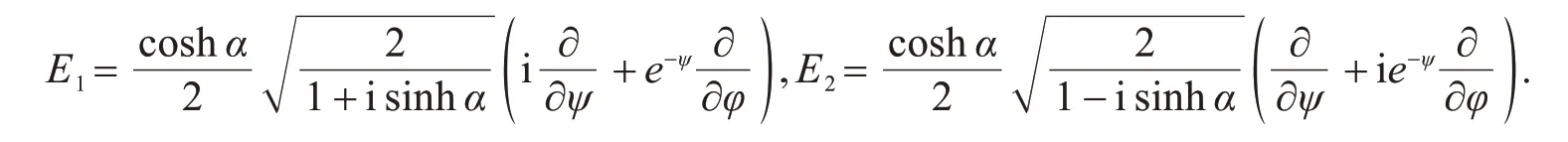
因此,该类曲面的李括号为