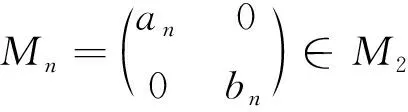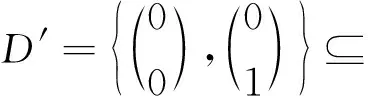平面上两个数字集生成的一类Moran测度的谱性

李海雄， 吴新林*， 丁道新

(1.湖北第二师范学院数学与经济学院， 武汉 430205； 2. 湖北第二师范学院大数据建模与智能计算研究所， 武汉 430205)

设μ是n上具有紧支撑的Borel概率测度，称μ为谱测度，如果存在n的离散子集Λ使得

E(Λ)∶={e-2πi〈λ，x〉:λ∈Λ}

成为L2(μ)上的规范正交基.集合Λ称为测度μ的谱. 也称(μ，Λ)为谱对.

研究一个具有紧支撑的Borel概率测度是否为谱测度是调和分析的一个基本问题，大量的研究谱测度的工作始于1974年Fuglede[1]提出的著名的谱集猜想.关于奇异测度的谱分析，最早是Jorgensen和Pedersen在文[2]中提出，他们指出四分Cantor测度是谱测度，而经典三分Cantor测度不能成为谱测度.众所周知，Moran测度是分形几何中一类典型奇异概率测度[3-4]，关于其谱性研究也一直是众多学者研究的兴趣之一. Strichartz[5]利用compatible tower，研究了一类Moran测度为谱测度的充分性. 最近安丽想和何兴纲[6]系统研究了一维情形下一类Moran测度为谱测度的特征刻画. 而关于一般Moran测度的谱性还可以参见文献[7-11].受上述文献的启发，本文主要考虑二维空间中，两个数字集所生成的Moran测度为谱测度的条件刻画.

设D为n中任意有限集，记这里#D表示集合D所含元素的个数，δd为点d处的Dirac测度.对于任意正整数n，设()为整扩张矩阵(即是矩阵Mn的所有特征值的模严格大于1)，Dn⊂2为数字集. 如果

则存在唯一具有紧支撑的Borel概率测度μ{Mn}，{Dn}，其定义如下：

μ{Mn}，{Dn}=

(1)

这里符号*表示两个测度的卷积且在弱收敛意义下定义其收敛性. 通常来说测度μ{Mn}，{Dn}称之为Moran测度[2-3]，且其支撑在Moran集T({Mn}，{Dn})上，其中T({Mn}，{Dn})定义如下：

T({Mn}，{Dn})=

(2)

本文总假设

这里对于任意n≥1有an，bn>1. 此时Moran测度μ{Mn}，{D}简记为μMn，D.如果所有扩张矩阵都相同，此时的Moran测度μMn，D称为自仿测度，记为μM，D[2-3]. 目前关于平面上2个数字集所生成的奇异测度的谱分析主要集中在自仿测度上，如李建林和文志英[12-13]系统刻画了扩张矩阵为整矩阵且数字集所含元素个数为2时，自仿测度μM，D为谱测度的刻画；随后戴欣荣等[14]、邓启荣等[15-16]将此结果推广到一般扩张矩阵且数字集含三个元素，也得到了自仿测度μM，D为谱测度的条件刻画. 以上结果表明，关于平面上自仿测度为谱测度的分析取得了很好的结果，但是对于一般Moran测度的谱性分析目前的研究还不多. 本文将主要研究一般Moran测度μMn，D的谱分析，通过构造一维2个数字集生成的Moran测度的谱，刻画μMn，D的谱性并给出其一组谱.

1 预备知识及引理

设μ是n上具有紧支撑的Borel概率测度，其Fourier变换定义为：

(3)

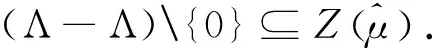
当Λ满足上式时，说Λ为测度μ的双零集. 因为双零集都具有平移不变性，所以本文总是假设0∈Λ，此时有Λ⊂Λ-Λ.

一般来说，当研究分形测度，特别是Moran测度的谱性时，都从下面的函数出发. 设ξ∈n，记

(4)

引理1[2]设μ是n上具有紧支撑的Borel概率测度，又设Λ⊂n为可数集，则

i) Λ为测度μ双零集当且仅当对于任意ξ∈n，有QΛ(ξ)≤1；

ii) Λ为测度μ的谱当且仅当对于任意ξ∈n，有QΛ(ξ)≡1.

特别地，如果Λ为测度μ双零集，则QΛ(z)为复平面上的整函数.

作为引理1的一个重要应用，可以得到下面关于非谱测度的一个条件刻画.

引理2[17]设μ=μ0*μ1是由n上两个概率测度形成的卷积测度，其中μ0，μ1均不为Dirac测度. 如果Λ⊂n为测度μ0的双零集，则Λ必为测度μ的双零集，但不能成为μ的谱.

2 主要结果及证明

对于任意n≥1，总假设an，bn>1，并且记

基于上面记号，得到下面关于Moran测度μMn，D为谱测度的充要条件.

定理1Moran测度μMn，D当且仅当对于任意n≥2，an为偶数.

证明对于任意的k，m∈0，如果k

(5)

为了证明本文定理，先证明充分性，即当n≥2，an为偶数时，Moran测度μ为谱测度.对于任意的m≥1，注意到Moran测度μ可以写成μ=μm*μ>m，这里

更进一步，还可以得到

ξ∈.

(6)

所以Moran测度μ的Fourier变换的零点集合为

记

接下来将证明Λ′为Moran测度μ的谱. 为此首先证明Λ′为Moran测度μ的双零集.对于任意λ1≠λ2∈Λ′，一定存在m1，m2∈0使得下式成立，

ck，ck′∈{0，(-1)k}.

设s≥1为满足cs≠cs′的最小指数，从而存在整数N满足

(7)

注意到cs-cs′不能被2整除且as+1为偶数，从而有

下面来证明E(Λ′)的完备性. 对于任意m∈0，记

类似于Λ′的正交性，容易得到Λ′m为测度μm的双零集. 注意到Λ′m恰好含有2m个元素，而Hilbert空间L2(μm)的维数恰好为2m，所以Λ′m为测度μm的谱. 特别地，根据引理1，有下面等式成立，

(8)

因为Λ′为Moran测度μ的双零集，由引理1知，对于任意ξ∈,

注意到Λ′m单调递增收敛到Λ′且μm弱收敛到μ，从而可以通过Lebesgue控制收敛定理来证明QΛ′(ξ)≡1.为此，对于任意给定的ξ∈，记

fm(λ)=|^μm(ξ+λ)|2,λ∈Λ'm;0,λ∈Λ'm,

f(λ)=|^μ(ξ+λ)|2,λ∈Λ';0,λ∈Λ'.

下面通过f(λ)来构造控制函数，对于任意λ∈Λ′m，首先有

(9)

对于任意给定的m∈0，如果λ∈Λ′m，则

如果m为奇数，类似可得

以及

这样就得到

所以有

(10)

因此，

(11)

这样上面的断言(8)式得证. 所以对于任意m∈0和λ∈Λ′m，进一步有

因为QΛ′(ξ)为整函数，所以对于任意ξ∈，有QΛ′(ξ)≡1. 从而根据引理1知，Λ′即为μ的谱集.

接下来将通过Λ′来构造Moran测度μMn，D的谱. 定义

这里ι:Λ′→是任意实值函数. 可说Λ为测度μMn，D的谱. 这是因为

(12)

所以就证明了定理的充分性.

关于必要性，将采用反证法来证明. 为此设存在n0≥2使得an0不为偶数.记M1，n=M1M2…Mn，又记Mn，1=MnMn-1…M1. 特别地,M1，1=M1.通过计算Mask函数MD的零点，有

所以,

注意到n0≥2，所以

M1，n0Z(MD)⊆M1，n0-1Z(MD).

记

类似的，对于任意n≥1，仍假设an，bn>1，记

则还可以得到下面定理.

定理2Moran测度μMn，D′当且仅当对于任意n≥2，bn为偶数.

证明根据定理1的证明，知当bn(n≥2)为偶数时，

为Moran测度

这里ι:Λ′→是任意实值函数. 类似于定义1的证明，可以得到Λ为测度μMn，D′的谱.反之亦类似，证毕.