基于不同截面形状的螺旋弹性管束换热器传热特性分析
2022-12-01季家东高润淼张经纬李飞扬
季家东,周 蓉,高润淼,张经纬,邓 旭,李飞扬
(1.安徽理工大学 机械工程学院,安徽 淮南 232001;2.安徽理工大学 人工智能学院,安徽 淮南 232001)
振动强化传热无需消耗额外能量,属于无源强化传热技术[1-2],是换热器研发、设计领域的主要内容之一。弹性管束换热器是一种利用振动实现强化传热的典型设备,其利用紫铜元件替代传统不锈钢元件,在保证使用寿命的同时,大幅提高传热性能。与传统平面弹性管束不同[3-4],螺旋弹性管束便于在换热器内实现顺/逆向密集布置,有利于换热器的总体传热性能的提高[5]。螺旋弹性管束的截面形状改变,会影响换热器内壳、管程流体的流动特性,进而影响螺旋管束的振动和传热特性。因此,基于管束的不同截面形状,研究螺旋弹性管束的传热性能,对于螺旋弹性管束换热器的设计和研发具有重要的理论和工程意义。
关于传统弹性管束及其换热器,大量科研人员[6-11]基于流体诱导振动、振动强化传热、管束结构改进等方面进行了许多卓有成效的研究。研究表明:传统弹性管束在低流速流体诱导下振动强化传热效果明显,且流体诱导振动的主因为壳程流体,振动主要表现为垂直于管束平面的面外振动。关于螺旋弹性管束换热器,Wu等[12]通过对一种螺旋管束换热器在壳程流体诱导下综合性能的研究发现:由于大量涡流的存在,增强了壳程流体的湍流特性,进而提高了换热器的综合传热性能。Ji等通过对换热器内单层双螺旋弹性管束传热性能的研究发现:螺旋管束的振动主要表现为垂直方向,换热器内上部管束的平均传热系数比下部管束的平均传热系数高约2.2倍。Khosravi-Bizhaem等[13]通过研究螺旋管中脉动流对传热特性的影响发现:在脉动流作用下,压降增加了3%~7%,换热性能提高了约39%。关于截面形状方面,Su等[14]基于三种截面形状对管束涡激振动特性和传热机理进行了研究,研究发现:在较低流速下,漩涡脱落力影响水平椭圆管的振动特性;当流体速度较大时,局部壁面涡流使得局部换热系数明显提高。
为探究截面形状对螺旋弹性管束传热性能的影响,本文以螺旋弹性管束四种截面形状(四边形、六边形、椭圆形和圆形)为出发点,以双向流固耦合(fluid structure coupling,FSC)计算的顺序求解法为基本手段,对单层四螺旋弹性管束在不同入口速度条件下的振动和传热特性进行了研究。
1 数值计算方法
1.1 螺旋弹性管束
单层四螺旋弹性管束换热器示意图,如图1所示。
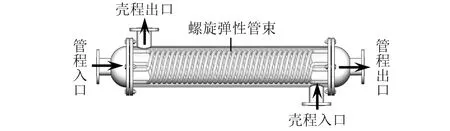
图1 螺旋弹性管束换热器Fig.1 Spiral elastic tube bundle heat exchanger
如图1所示,四根尺寸一致的螺旋弹性管束等间距的安装在换热器左右管板上,管程热流体从左侧管程入口流入换热器左封头区域,通过左管板孔流入四根螺旋弹性管束,经右管板孔流入换热器右封头区域,从右侧管程出口流出。壳程冷流体从底部壳程入口流入换热器内部,冲刷螺旋弹性管束后从顶部壳程出口流出。冷热流体相互作用,耦合诱导螺旋弹性管束振动,进而实现强化传热。
1.2 流体域和结构域
图2所示为螺旋弹性管束流体域及结构域。因壳程流体为管束振动的主因,计算仅保留壳程流体。图2中:L为流体域或螺旋管长度;P为螺距;Dh为螺旋直径;M为壳程出、入口距离流体域左、右端间距;R1为壳程出、入口流体域半径;R2为流体域半径。为便于说明,将管束编号为1~4,并标记为i(i=1~4)。此外,为分析管束截面圆周的局部传热性能,选取四个截面位置为分析对象(图示Ⅰ、Ⅱ、Ⅲ、Ⅳ),编号与管束编号相对应。
计算过程中,结构参数设置如下:L=600 mm,P=100 mm,Dh=100 mm,M=30 mm,R1=20 mm。为便于对比,不同截面形状的管束设置相同的壁厚(δ=1.0 mm)和相同的截面积(S=78.5 mm2)。
螺旋弹性管束的材料为紫铜,物性参数为:密度ρp=8 900 kg/m3,弹性模量Ep=1.29×1011Pa,泊松比υp=0.33。
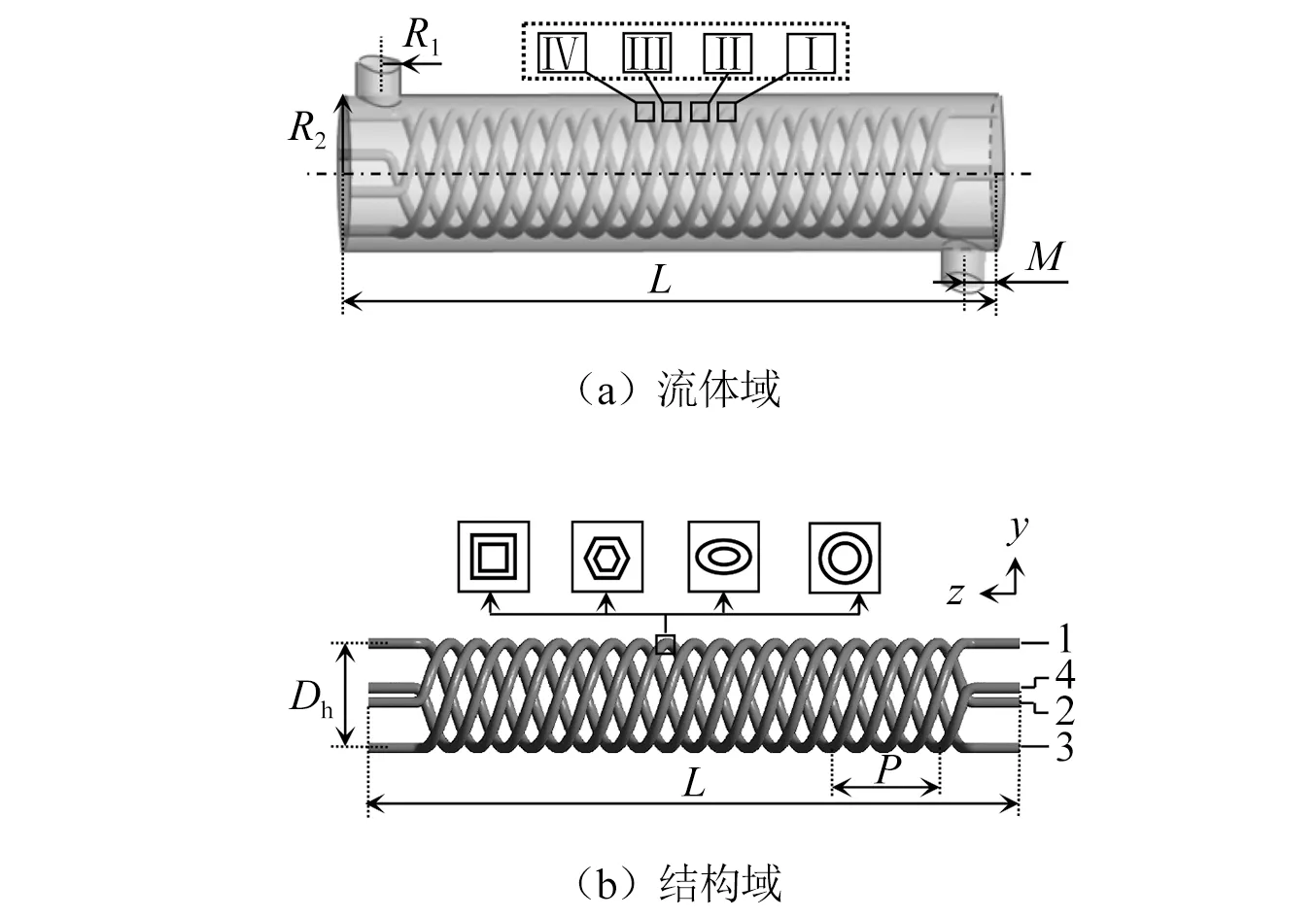
图2 流体域和结构域Fig.2 Fluid domain and structural domain
1.3 数值方法
计算过程中,流体介质为不可压缩流体——水。热物性参数取决于流体平均温度,且不考虑热损失。流体域计算采用ANSYS CFX软件,结构域计算采用ANSYS Workbench平台的Transient Structural模块。流体域边界设置:入口设置为“Inlet”,给定入口流体速度(vin=0.1 m/s,vin=0.4 m/s,vin=0.7 m/s)和温度(Tin=293.15 K);出口设置为“Outlet”,给定出口 相对压力(Pre=0);设置与管束接触的壁面为FSC交界面,给定壁面温度(Twall=333.15 K)。结构域边界条件:螺旋弹性管束的两端面均设置为“Fixed Support”;螺旋弹性管束的壁面均设置为FSC交界面,对应于流体域的FSC交界面;设置重力加速度方向为-y方向,其值为:9.807 m/s2。
基于考虑FSC交界面的能量损失,系统有限元波动方程为
(1)
基于哈密尔顿原理,含流体力的结构力学方程为
(2)
式中:下标f为流体;下标p为结构;M,C,K分别为质量、阻尼和刚度矩阵;u为速度矢量;p为流体动压;RT为FSC交界面的耦合矩阵;Fp和Ff分别为结构场内部作用力和流体作用力。
联立式(1)和式(2),可得FSC问题的有限元离散方程为
(3)
FSC计算时,流体域和结构域的数据传递通过FSC交界面实现,且遵循如下守恒
nfτf=npτp
(4)
sf=sp
(5)
式中:n为FSC交界面的法向矢量;τ为FSC交界面的压力;s为FSC交界面的位移。
计算满足如下条件时,计算结束。
(6)
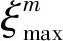
为得到稳定流场的传热数据,将计算过程分两步进行:粗算和精算。粗算:基于流场初始边界条件,启动CFX解算器对流体域进行计算,直至壳程流场获得充分发展。精算(计算流程见图3):① 以粗算后流场条件为初始条件,启动CFX解算器对流体域进行第一步计算,将计算后的压力通过FSC交界面传递到结构域;② 以FSC交界面传递的流体力为初始条件,结合结构域初始边界条件,启动ANSYS解算器对结构域进行第一步计算,将计算后的位移通过FSC交界面传递到流体域;③以FSC交界面传递的位移为初始条件,结合第一步计算的流场条件,启动CFX解算器对流体域进行第二步计算,将计算后的压力通过FSC交界面再次传递到结构域;④ 以FSC交界面传递的流体力为初始条件,结合结构域第一步计算的结果,启动ANSYS解算器对结构域进行第二步计算,将计算后的位移通过FSC交界面再次传递到流体域;⑤ 如此交替计算,直至完成所有时间步。
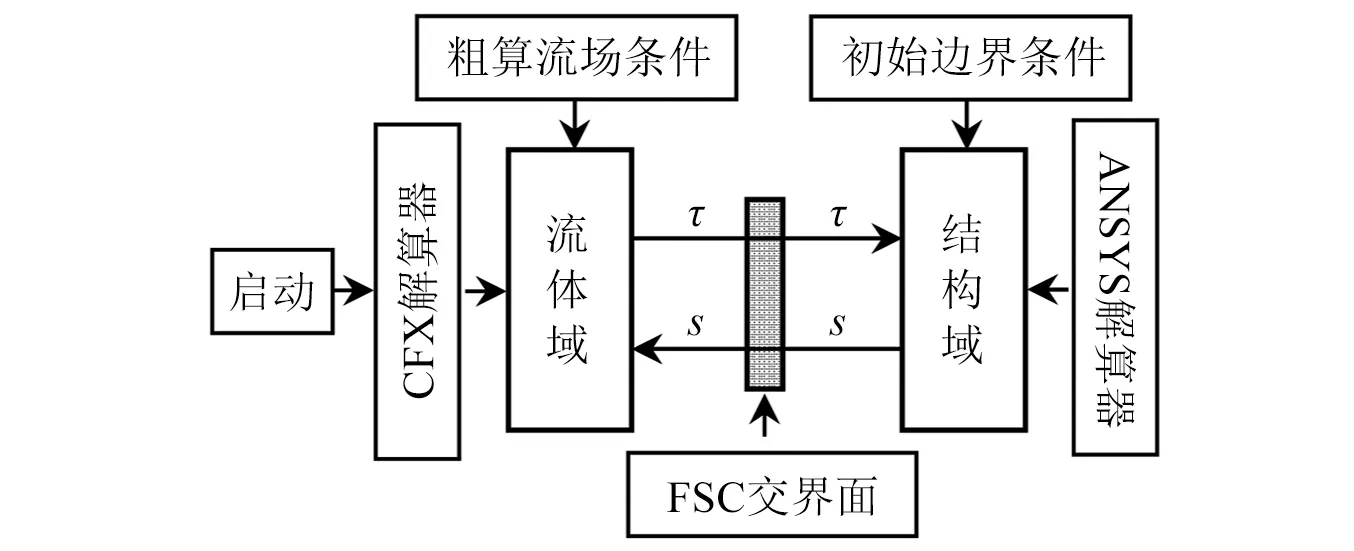
图3 FSC计算(精算)流程Fig.3 Process of FSC calculation (accurate calculation)
粗算过程中,为使流场获得充分发展,设置计算时间为300 s,时间步长为0.1 s。经验证,该时间及步长设置能够使本文计算流速条件下(vin=0.1 m/s,vin=0.4 m/s,vin=0.7 m/s)的流场获得充分发展。精算过程中,为捕捉到精确的振动波,设置计算时间为1.2 s,时间步长为0.001 s。经验证,该时间及步长设置满足计算要求(参见1.5节结果验证)。
1.4 网格划分
图4所示为流体域和结构域网格,网格划分采用ANSYS Workbench平台的Meshing模块执行。结构域划分为六面体网格,流体域划分为四面体网格,且流体域内部近壁区设置6层边界层网格。
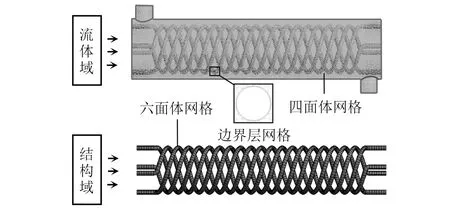
图4 流体域和结构域网格Fig.4 Grids of fluid domain and structural domain
基于不同截面形状的流体域和结构域的网格数和节点数,如表1所示。经试算,进一步增加网格数目和边界层数对计算结果的影响不大,网格满足独立性。

表1 网格数和节点数Tab.1 Number of grids and nodes
1.5 数据处理
管束在振动条件下面均传热系数的表达式为
h=q/ΔT
(7)
其中,
(8)
式中:q为壁面热流密度;ΔT为对数平均温差;Tin和Tout分别为壳程进出口流体的平均温度;Twall为壁面温度。
此外,为分析换热器内所有管束的平均传热性能,定义平均传热系数为
(9)
式中:i为管束编号;n为管束数目;hi为管束i的面均传热系数。
1.6 结果验证
文献[15]研究了螺旋管束壳程振动强化传热特性,所用螺旋管束与本文螺旋弹性管束的结构、材料、流体介质均一致。为验证本文计算结果的有效性,基于Jamshidi等建立的单螺旋弹性管束计算模型,采用本文粗算加精算的计算方法和网格划分方法,对振动条件下的努塞尔数(Nu)进行了计算,并与试验结果进行了对比,如图5所示。

图5 模拟结果与试验结果的对比Fig.5 Comparison between simulation results and experimental data
从图5可以看出,不同雷诺数Re条件下模拟结果与试验结果的差距不大,最大相对误差仅为3.05%。这说明,本文粗算加精算的计算方法和网格划分方法是合理的且有效的。
2 结果与讨论
2.1 振动响应分析
图6所示为基于管束不同截面形状的速度矢量图。图示截面为y-z面,vin=0.1 m/s。
从图6可以看出:
(1) 流体进入换热器后,首先冲击壳程入口附近管束,而后冲击换热器内壁,改变流动方向后近似螺旋向左推进,最后从壳程出口流出。
(2) 不同截面形状管束的速度分布不同,流体域上侧流动更加强烈,且由于管束绕流作用,在流场内产生大量回流及涡流。
(3) 局部放大图显示,壳程流体主要以轴流方式冲刷管束,同时也会在其尾流区域产生一定的螺旋流。
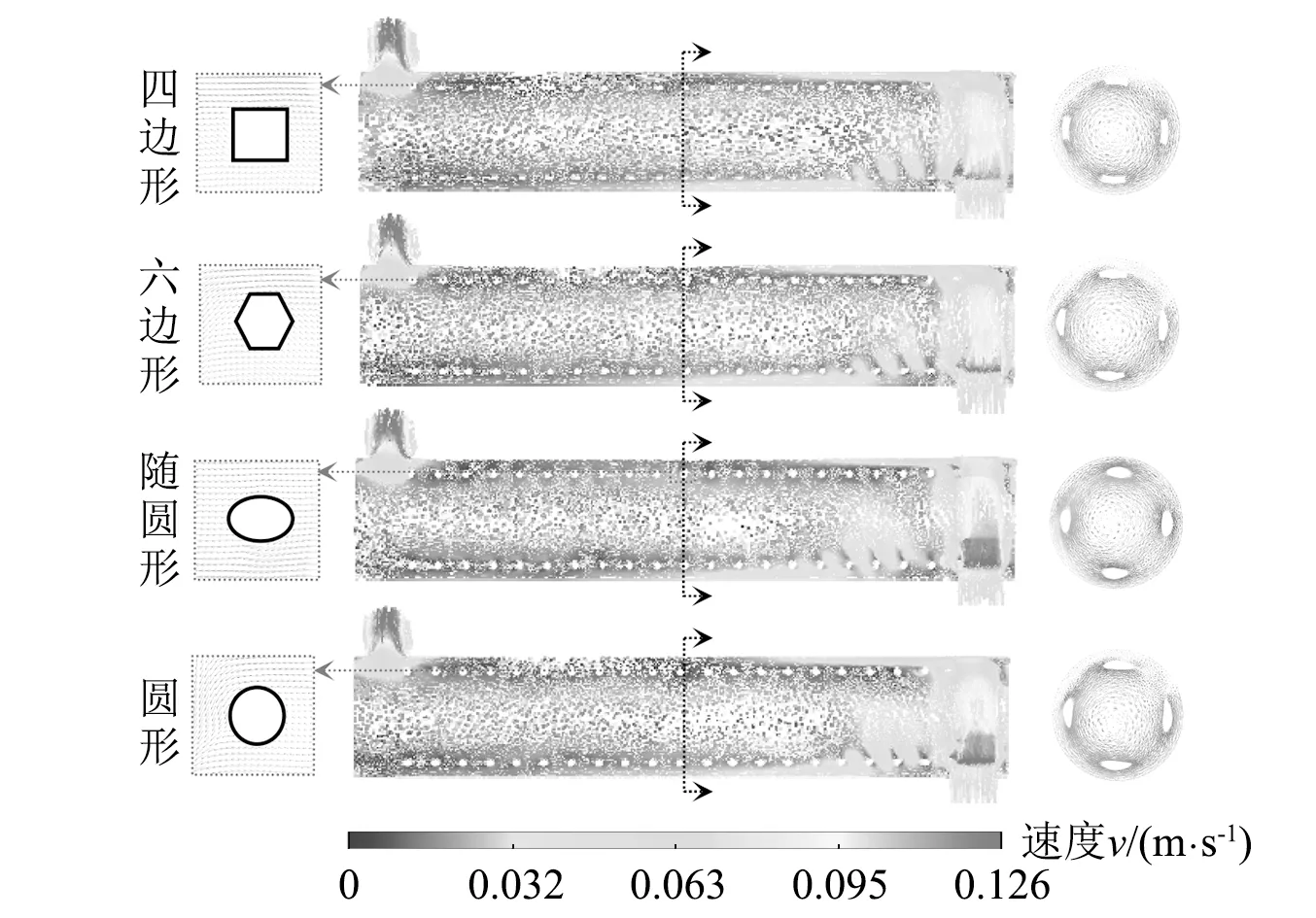
图6 基于不同截面形状的速度矢量图Fig.6 Velocity vector diagram based on different section shapes
为了对壳程流体诱导下螺旋弹性管束的振动响应进行分析,在每根管束的中心位置设置监测点。表2所示为不同截面形状下监测点的振幅(A)和频率(f)情况。其中,vin=0.1 m/s。
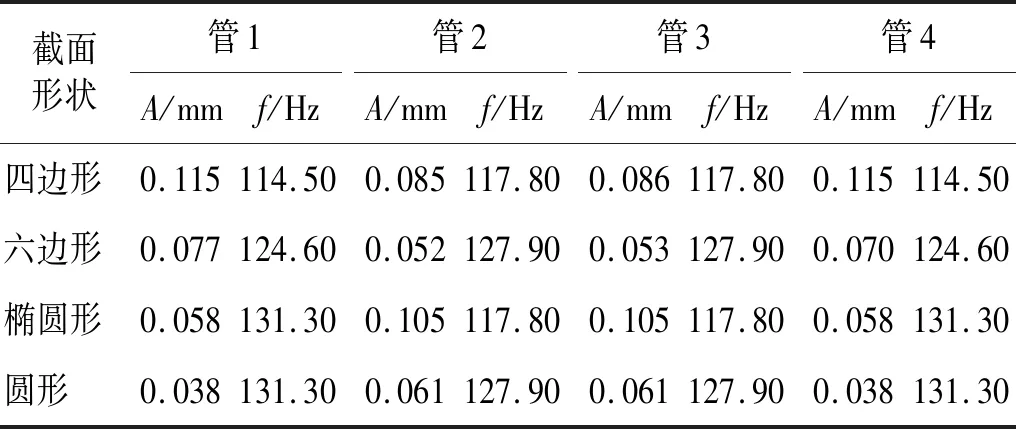
表2 不同条件下监测点的频率和幅值Tab.2 Frequency and amplitude of monitoring points under different conditions
从表2可以得出:
(1) 对于四边形和六边形截面,管1、管4的振动较剧烈,且振动频率略低;对于椭圆形和圆形截面,管2、管3的振动较剧烈,且振动频率略低。
(2) 对于管1、管4而言,振幅由高到低,截面形状依次为:四边形、六边形、椭圆形、圆形;对于管2、管3而言,振幅由高到低,截面形状依次为:椭圆形、四边形、圆形、六边形。
综上,由于壳程流场的作用,不同截面形状的螺旋弹性管束在换热器内不同安装位置的振动响应有明显的不同。对于管1、管4而言,截面为四边形的螺旋弹性管束的振动最剧烈,对于管2、管3而言,截面为椭圆形的螺旋弹性管束的振动最剧烈。
2.2 不同截面形状的传热性能
图7所示为基于管束不同截面形状的温度场分布云图。图示截面为y-z面,vin=0.1 m/s。
从图7可以看到:
(1) 由于螺旋弹性管束的振动传热作用,壳程入口的低温流体逐渐被加热后从壳程出口流出。

图7 基于不同截面形状的温度场分布云图Fig.7 Temperature distribution nephogram based on different section shapes
(2) 截面为四边形、六边形和圆形的管束在顶部靠近壳程出口处存在高温流体集中区域。
(3) 截面为椭圆形的管束温度场的过度更加均匀,且在顶部的高温流体集中区域很小。
图8所示为振动条件下基于管束不同截面形状的单根管束传热系数(hi)分布情况。其中,vin=0.1 m/s。
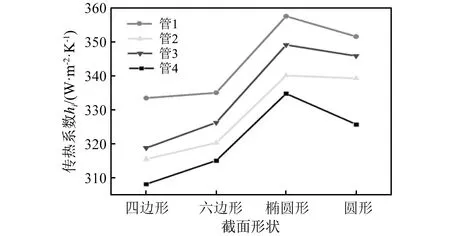
图8 基于不同截面形状的振动传热系数Fig.8 Vibration heat transfer coefficients based on different section shapes
从图8可以看到:
(1) 相同截面形状条件下,管1在振动条件下的传热系数均最高,说明管1的传热性能最佳。
(2) 不同截面形状条件下管束的传热性能不同,截面为椭圆形的管束在振动条件下的传热系数最高、圆形次之、四边形最低,说明管束截面形状为椭圆时的传热性能最佳。
为了进一步分析螺旋弹性管束的振动强化传热性能,基于不同的截面形状,计算了管束在不振动条件下的平均传热系数(ha),并与振动条件下的平均传热系数进行了对比,如图9所示。其中,vin=0.1 m/s。
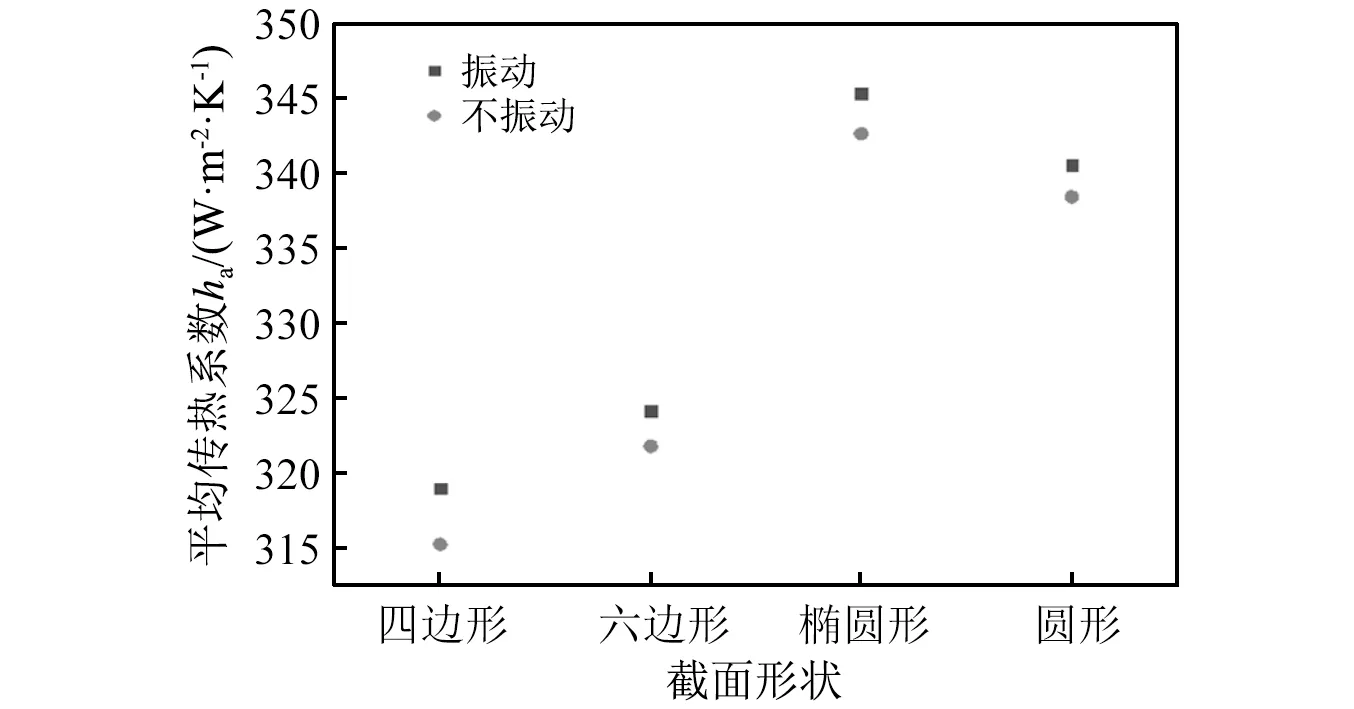
图9 振动与不振动条件下不同截面形状管束的平均传热系数Fig.9 Average heat transfer coefficients of tube bundle with different cross-sections under vibration and non-vibration conditions
从图9可以看到:
(1) 振动条件下下管束的平均传热系数均高于不振动条件下的平均传热系数,说明流体诱导管束的振动实现了强化传热。
(2) 振动和不振动条件下截面为椭圆形的管束的平均传热系数均为最高,进一步说明管束截面形状为椭圆时的传热性能最佳。
结合前面对振动响应的分析,对于管1、管4,截面为四边形的螺旋弹性管束的振动最剧烈,但截面为椭圆形管束的传热性能最佳;对于管2、管3,截面为椭圆形的螺旋弹性管束的振动最剧烈,且截面为椭圆形管束的传热性能最佳。这说明,振动能够实现强化传热,但振动剧烈的管束其传热性能并不一定是最佳,这种结论区别于Duan等、Ji等(2021年、2018年)的研究结论。因此在进行螺旋弹性管束换热器设计时,并不是要一味追求高强度的振动,还要综合考虑螺旋弹性管束的安装位置和截面形状。
2.3 不同入口流速的传热性能
图10所示为振动条件下基于不同壳程入口流速的管束平均传热系数(ha)的分布情况。

图10 不同入口流速条件下不同截面形状管束的平均传热系数Fig.10 Average heat transfer coefficients with different cross-sections under different inlet flow rates
从图10可以看到:
(1) 不同截面形状管束的平均传热系数均随流速的增加而增加,当流速0.1 m/s从增加到0.7 m/s时,截面为四边形、六边形、椭圆形和圆形的平均传热系数分别提高了254.9%,259.2%,294.3%和263.8%,说明截面为椭圆形的管束的传热性能受流速的影响最大。
(2) 同一流速条件下,截面为椭圆形的管束的平均传热系数均为最高。当vin=0.7 m/s时,其相对于截面为圆形、六边形和四边形管束的平均传热系数分别提高了20.3%,17.0%,9.9%。说明不同流速条件下椭圆形管束的传热性能始终为最优。
为了进一步分析螺旋弹性管束的振动强化传热性能,基于不同的壳程入口流速,计算了截面为椭圆形的管束在不振动条件下的平均传热系数(ha),并与振动条件下的平均传热系数进行了对比,如图11所示。
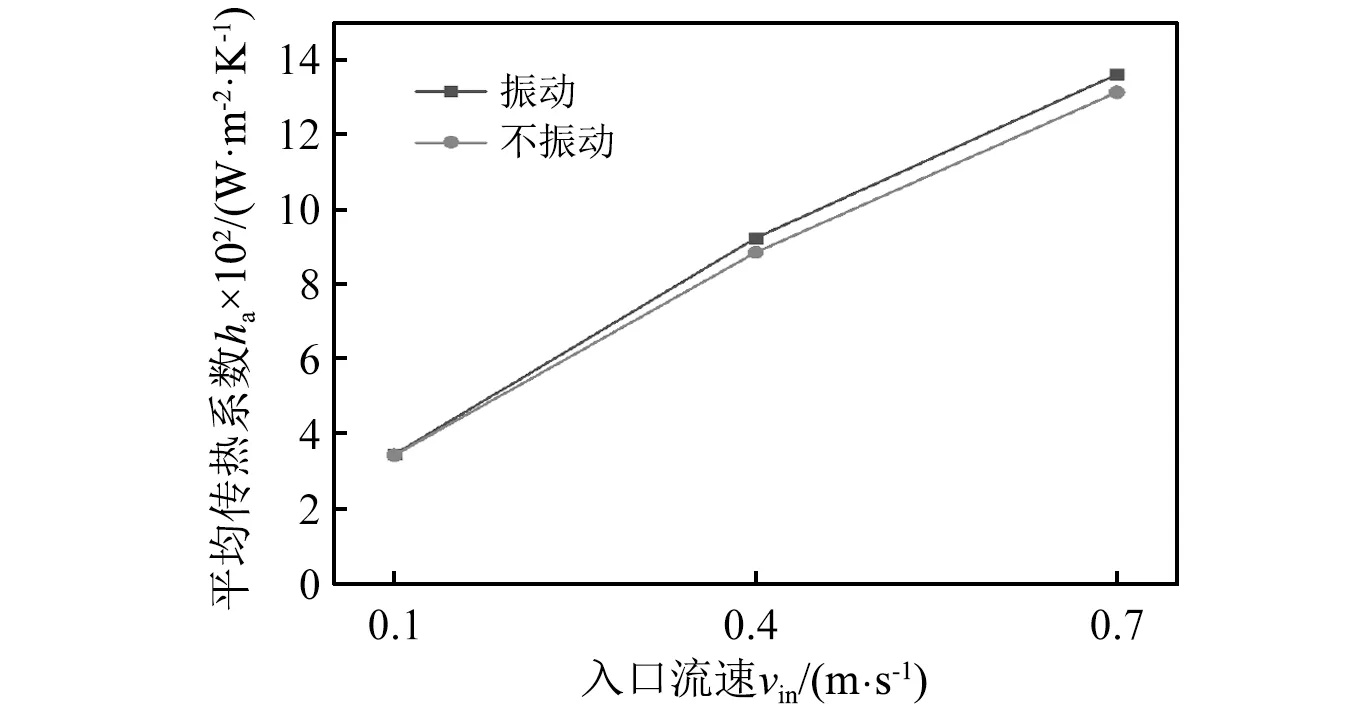
图11 椭圆形管束振动与不振动时的平均传热系数Fig.11 Average heat transfer coefficients of tube bundle with elliptical cross section under vibration and non-vibration conditions
从图11可以看到:
(1) 不同流速条件下,截面为椭圆形的管束在振动条件下的平均传热系数分别提高了0.8%,4.2%和3.5%,振动条件下的平均传热系数均高于不振动条件下的平均传热系数。
(2) 当流速0.1 m/s从增加到0.7 m/s时,不振动条件下的平均传热系数增加了283.4%,振动条件下的平均传热系数增加了294.3%,说明管束在振动条件下传热性能受流速的影响更加明显。
(3) 结合前面的分析(见图10),与振动强化传热相比,管束截面形状的改变对管束的传热系数影响更大。
2.4 截面圆周局部传热性能
为了分析管束在截面圆周上的局部传热性能,基于图2所示的四个截面位置Ⅰ、Ⅱ、Ⅲ、Ⅳ,分析了不同截面形状条件下管束截面圆周的局部传热性能,如图12所示。其中,vin=0.7 m/s。
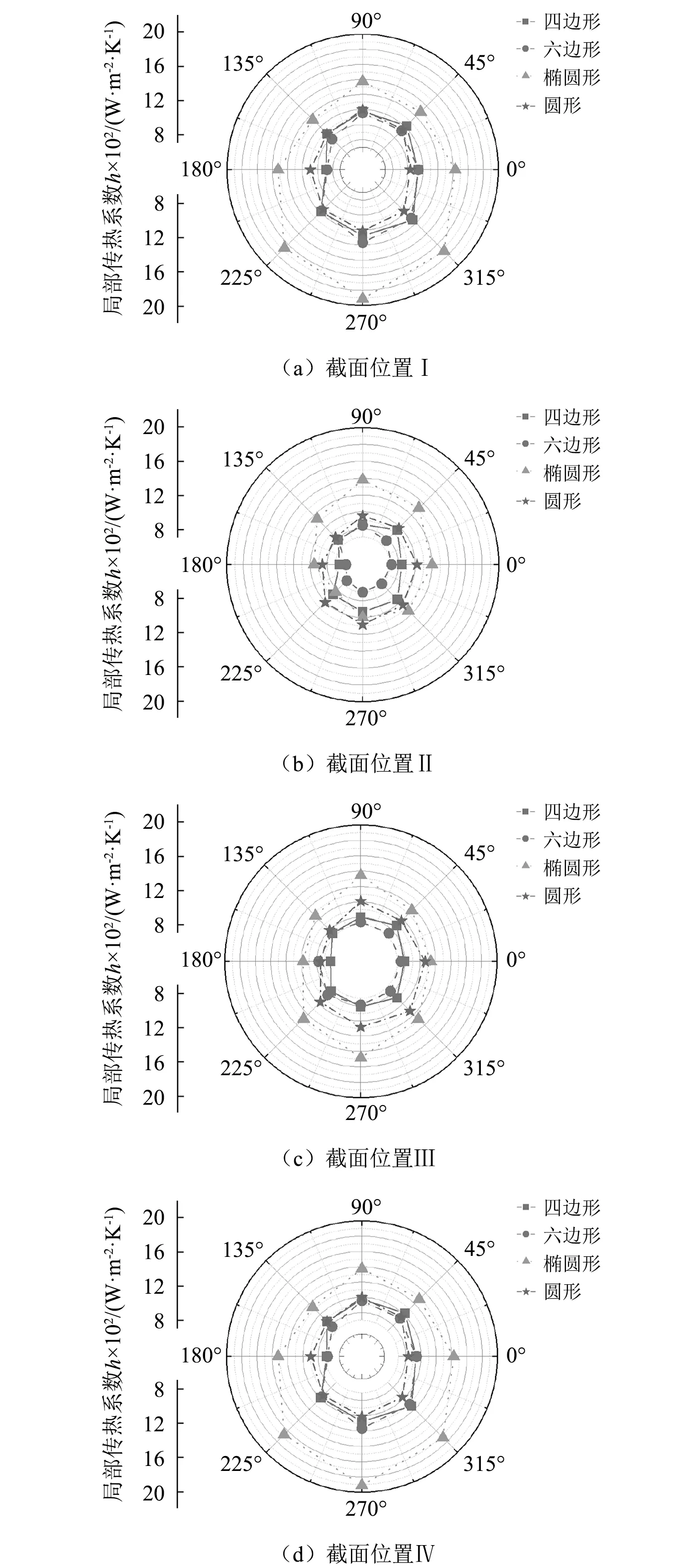
图12 不同条件下的局部传热系数Fig.12 Local heat transfer coefficients under different conditions
从图12可以看到:
(1) 同一截面位置处,截面形状为椭圆形的管束圆周上的局部传热系数均为最大,说明截面为椭圆形的管束局部传热性能最优。
(2) 不同截面位置处,基于相同截面形状的圆周上的局部传热系数大小不一,这是由于不同截面处管束周围流体的流动方向和大小不同所致。
(3) 总体来看,截面圆周270°(或90°)处局部传热系数为最大,180°处局部传热系数为最小。这是由于壳程流体绕流管束后引起的低压及回流现象所致。
3 结 论
为探究截面形状对螺旋弹性管束传热性能的影响,基于四种截面形状(四边形、六边形、椭圆形和圆形),采用双向FSC计算,对单层四螺旋弹性管束在不同入口速度条件下的振动和传热特性进行了研究。主要结论如下:
(1) 由于螺旋弹性管束的绕流作用,在换热器壳程流场内产生大量回流及涡流,致使不同截面形状的螺旋弹性管束在换热器内不同安装位置的振动响应有明显的不同。
(2) 不同流速条件下,截面为椭圆形的螺旋弹性管束在振动和不振动条件下的传热系数最高,说明管束截面形状为椭圆时的传热性能最佳。
(3) 振动能够实现强化传热,但振动剧烈的管束其传热性能并不一定最佳,在进行螺旋弹性管束换热器设计时,并不是要一味追求高强度的振动,还要综合考虑螺旋弹性管束的安装位置和截面形状。
(4) 同一截面位置处,截面形状为椭圆形的螺旋弹性管束截面圆周均具有最大的局部传热系数。由于壳程流体绕流管束引起的低压及回流现象,截面圆周270°(或90°)处的局部传热系数为最大,180°处的局部传热系数为最小。
