基于大型声学风洞的飞行器起落架噪声试验研究
2022-12-01梁俊彪KopievVictorBelyaevIvan
赵 鲲,梁俊彪,Kopiev Victor ,Belyaev Ivan
(1.中国空气动力研究与发展中心 低速空气动力研究所 气动噪声控制重点实验室,四川 绵阳 621000;2.俄罗斯中央空气流体动力研究院 气动噪声部,莫斯科 105005)
随着航空航天科技高速发展,飞行器数量剧增,伴随而来的噪声排放问题日益引起世界范围内的密切关注。以大型民用客机为例,2017年12月31日,美国联邦航空管理局(FAA)和国际民航组织环境保护委员会 (CAEP) 开始采用的第五阶段适航噪声标准,对优化航空业噪声环境提出更高要求,同时也为其他发展大客的国家增加了新的技术挑战与壁垒。因此,我国研制的ARJ、C919及中俄联合研制的CR929等民用飞机要进军国际市场,噪声问题必须得到有效解决。
飞行器排放噪声主要分为发动机噪声和机体噪声两大类[1]。自二十世纪七十年代起,随着大涵道比结构、锯齿尾缘等一系列降噪技术的成功应用[2],发动机噪声显著下降,这使得机体噪声比重大幅度增加,成为重要噪声源。机体噪声主要来自增升装置(缝翼、襟翼等)、起落架等部件,是由高速来流与其固体表面相互作用而产生,其作为“航空器噪声障碍(aircraft noise barrier)”,是气动声学研究领域的热点[3]。
起落架是飞行器着陆时承载全部质量的核心部件,具有精密力学结构。由于起落架是关系到飞机安全的重要部件,传统的起落架结构是以实现安全性、可靠性为前提的最优设计,在噪声辐射方面未有足够考虑。这就导致了多种气动噪声源直接暴露在高速来流中,伴随产生大尺度流动分离、漩涡脱落、尾迹与下游物体干涉等现象,造成严重噪声污染。此外,湍流边界层与空腔共振等现象令其噪声问题更加复杂[4-5]。因此,起落架降噪技术是当前气动声学领域的一个热点问题。
中国空气动力研究与发展中心(以下简称“气动中心”)与爱尔兰圣三一学院联合团队对当前世界上公开发表文献中的起落架降噪技术进行了综述,总结了包括整流罩(轮毂盖)、部件优化、舱体前缘锯齿、空气幕等各类主动、被动控制方法。然而,由于技术成熟度较低,即使具有较好前景,绝大多数方法目前仍未得到商业应用,起落架噪声问题仍是民机噪声控制领域的关键障碍。因此,对起落架噪声特征及相关产生机理研究十分必要。
当前,起落架噪声研究主要包括以下手段:风洞试验[6-11]、数值模拟[12-15]、飞行试验[16]、理论分析与半经验公式相结合的模型预测[17-19]等。风洞试验,特别是声学风洞试验可以提供所需且可控的流场与声学环境;与飞行试验对比成本相对较低,与数值模拟和模型预测相比具有更高的可靠性,因此在起落架噪声研究领域被广泛运用。例如,在新型降噪技术概念验证领域,小尺度声学风洞试验已成为一种普遍手段。然而受缩比限制,模型缺少几何细节,小尺度试验并不能反映许多真实特征。此外,数值模拟与模型预测工作均需要准确的试验数据与验证,因此开展大尺度试验研究非常必要。
2018年,中国空气动力研究与发展中心与俄罗斯中央空气流体动力研究院(TsAGI)在两国政府的支持下,共同承担了“面向飞行器起落架降噪技术的针对不同尺度模型的噪声产生机理研究”项目,主要针对大尺度起落架开展噪声特性研究,达到进一步认清噪声产生机理,开发新型降噪方法的目的,为两国共同研制的大型民用客机的低噪声设计提供支撑。本文工作是该项目中的一部分联合试验内容。
本文以气动中心FL-17 5.5 m×4.0 m航空声学风洞和相关配套声学测量设备为研究手段,开展了大尺度起落架噪声试验。模型采用模块化设计,通过参数化试验方法,研究了不同状态下起落架噪声特性,包括风速、高度、轮直径、攻角、轮数、轮攻角等。本文研究成果对飞行器起落架低噪声优化与设计具有较好的指导意义。
1 试验设备与模型
1.1 FL-17 5.5 m×4.0 m航空声学风洞
试验在中国空气动力研究与发展中心5.5 m×4.0 m航空声学风洞(FL-17)开展,如图1所示,该风洞是一座单回流式低速低湍流度声学风洞,具有开口、闭口两个可更换试验段,本次试验是在开口试验段进行。该试验段长14 m,横截面为矩形,高4.0 m、宽5.5 m,最大风速100 m/s,主要用于声学试验,其背景噪声为75.6 dB(A)(距喷管出口中心侧向距离7.95 m处,截止频率200 Hz,风速80 m/s),中心区域气流湍流度≤0.05%。开口试验段外包围着一个内部净空尺寸为26 m(宽)×18 m(高)×27 m(长)的全消声室,截止频率100 Hz。
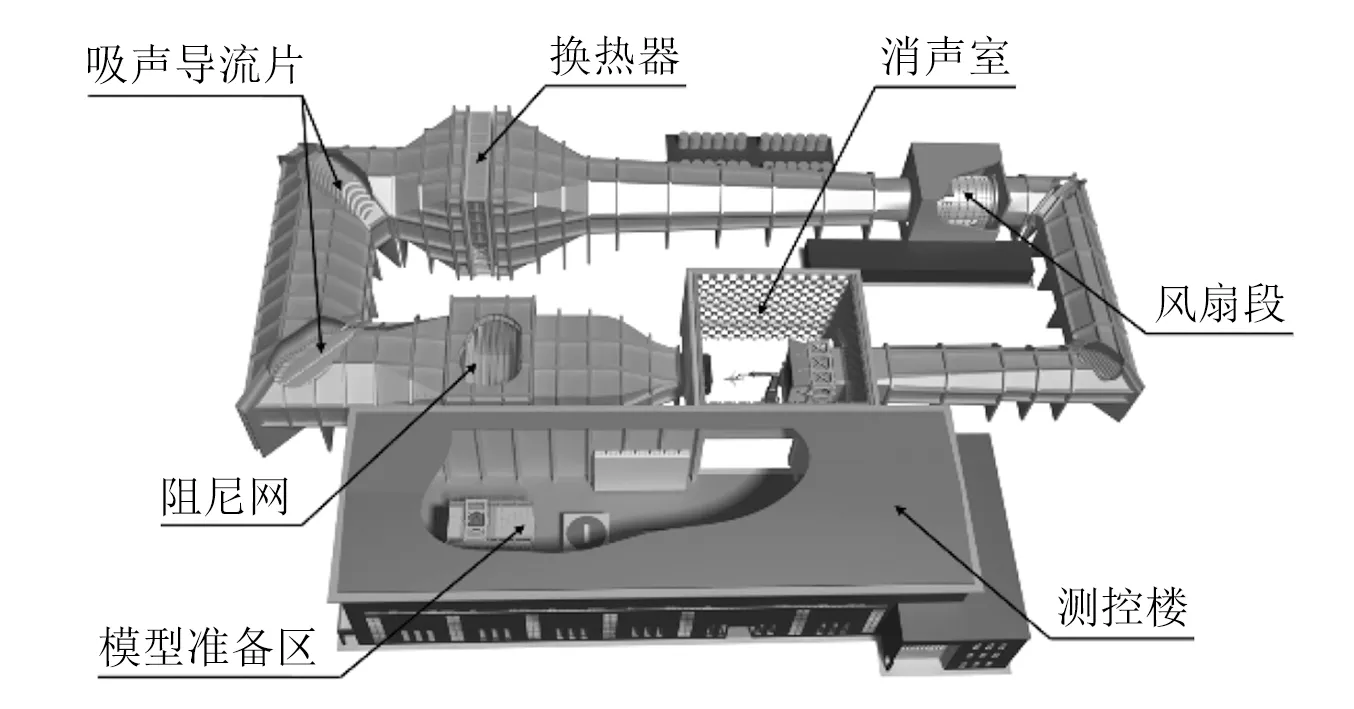
图1 FL-17 5.5 m×4.0 m航空声学风洞总体结构示意图Fig.1 Outline of the FL-17 5.5 m×4.0 m aeroacoustic wind tunnel
1.2 3/4开口试验段
3/4开口试验段是为FL-17风洞设计的多功能模型支撑平台,其结构如图2所示。地板长13 500 mm,宽8 600 mm,标高6 000 mm,前缘与风洞喷口无缝联接。地板分为硬质地板和穿孔板两种构造,本试验采用穿孔板地板。该结构采用消声处理,穿孔板下层布置吸声尖劈,可有效降低地板噪声反射,便于开展声场测试工作。
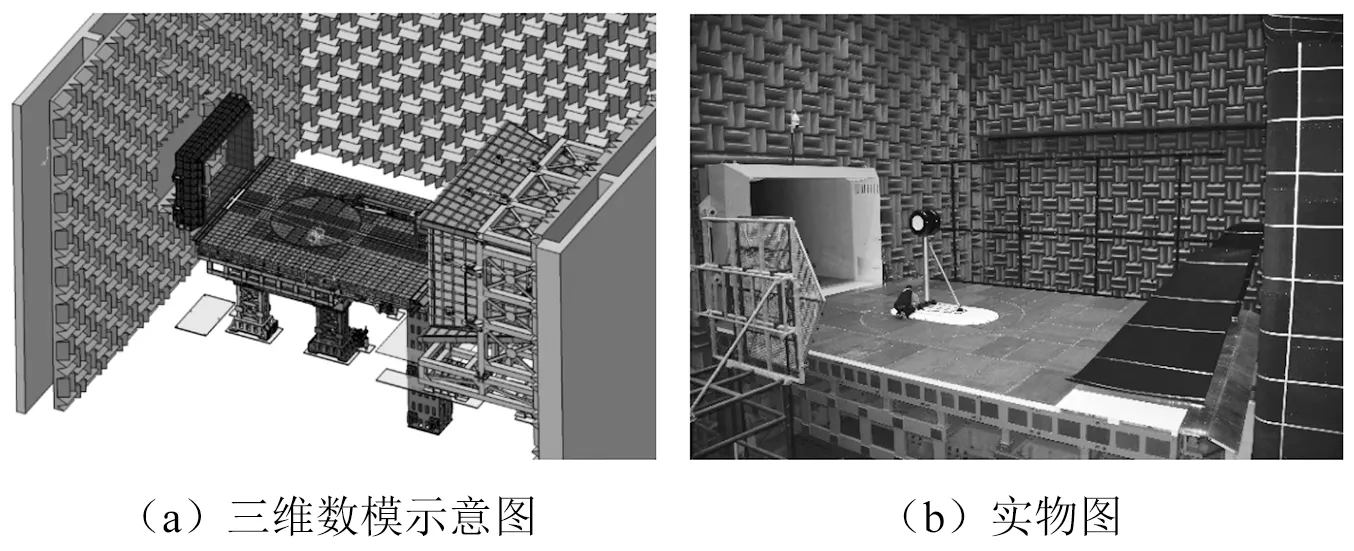
图2 3/4开口试验段Fig.2 3/4 open test section
1.3 试验模型
试验模型由气动中心和TsAGI联合设计制造,与我国自行研制的C919飞机起落架尺度相当,属于大尺度工程简化模型,实物如图3所示。为方便研究,该模型简化了真实起落架的细节机械结构,但覆盖典型声源类型与重要小尺度部件,因此试验研究结果对工程中的起落架低噪声设计具有较为重要的参考价值。该模型主要包括支柱、轮胎、支杆等部件,如图4所示。整个模型通过外筒底部连接轴与底座连接,底座与试验支撑平台固联。为避免额外噪声产生,底座与连接轴都配备整流罩实现光滑过渡。

图3 模型模块实物图Fig.3 Photo of the test model modules
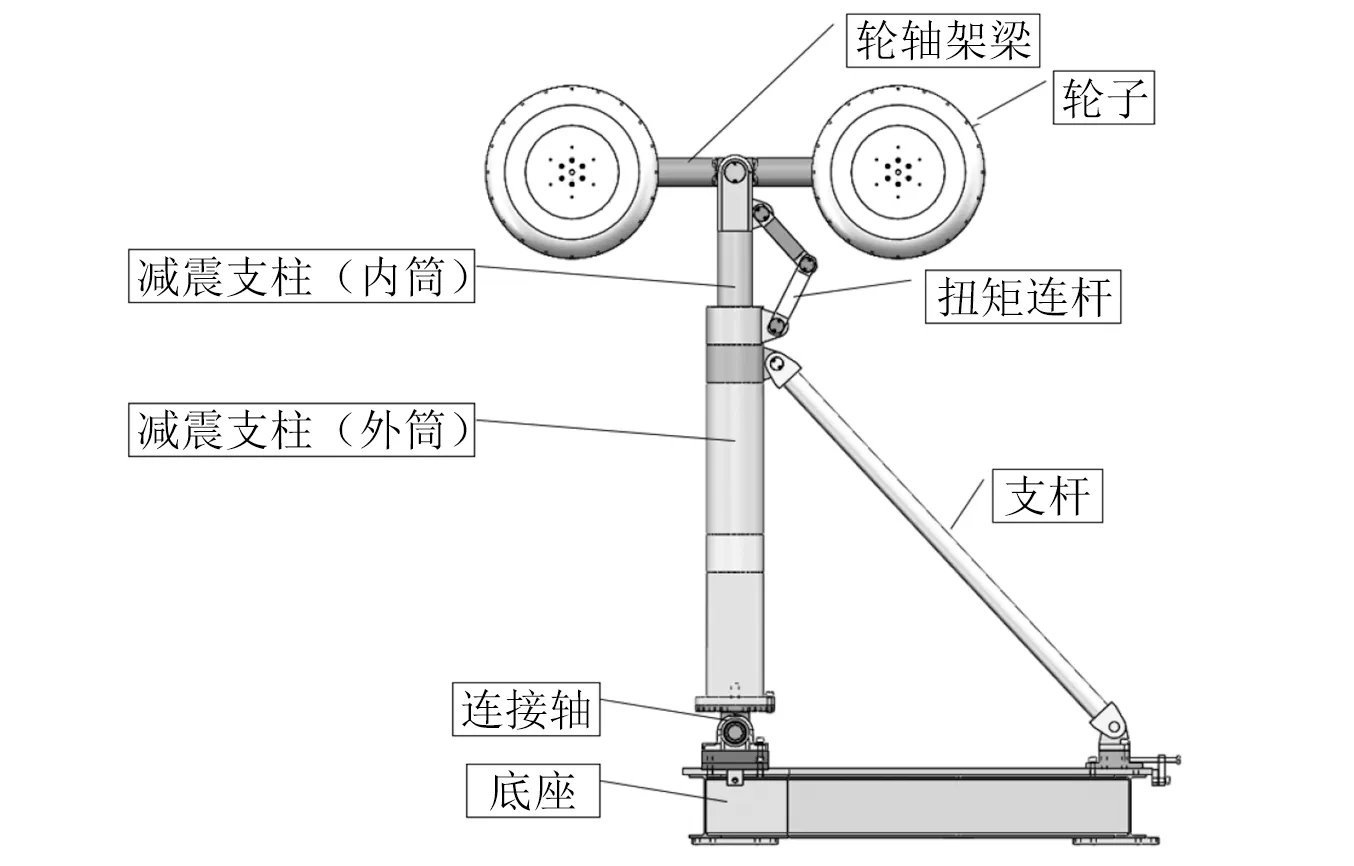
图4 起落架主要部件示意图Fig.4 Sketch of the landing gear model key element
为研究各参数对起落架噪声影响,模型采用模块化设计,确保各个部件可拆卸更换,从而能够研究不同构型下起落架噪声特征及声源分布规律。通过模型变换,可实现研究的起落架参数包括:不同高度h、不同轮直径φ、不同攻角α、不同轮数、不同轮攻角αw、不同偏角β。
1.3.1 不同高度h
为研究起落架高度对噪声特性影响,模型以两轮型为基础,通过变化外筒,采用了三种高度进行试验,即低高度、中高度和高高度,具体如图5所示。在高度变化过程中,为确保攻角与来流的相对位置,根据相应几何关系,对支杆进行了适应性变化,从而实现与外筒进行匹配。
1.3.2 不同轮直径φ
起落架设计过程中,轮尺寸对噪声具有一定影响。为此,模型以两轮型为基础,对轮子进行了更换,进而研究噪声特性。所更换的即为四轮与六轮起落架结构中的轮子,三种尺寸分别为:φ=720 mm(大轮),546 mm(中轮)和480 mm(小轮),具体如图6所示。

图5 不同高度起落架模型(mm)Fig.5 Models with different height(mm)

图6 不同轮直径φ起落架模型(mm)Fig.6 Models with different diameter φ(mm)
1.3.3 不同攻角α
起落架在收放过程中,其攻角α会经历一个连续变化过程,对噪声特征也会产生影响。为此,本文利用图4所示连接轴,并同时更换支杆,对攻角进行了控制,实现α=90°,α=70°,α=50°和α=30° 4个值,具体如图7所示。
1.3.4 不同轮数
当前,起落架根据轮数特征,主要可分为两轮型、四轮型和六轮型三大类。为评估不同轮数对起落架噪声影响,本文对三种结构进行了试验分析,具体参数与构型如图8所示。
1.3.5 不同轮攻角αw
本文针对四轮与六轮型起落架构造,定义轮攻角αw为轮轴架梁与来流夹角,具体如图9所示。在起落与着陆过程中,轮攻角会根据当前姿态进行调整,进而影响噪声特征。为此,本文对四轮结构起落架进行了分析,比较了αw=24°,αw=12°,αw=0°,αw=-12°和αw=-24°,其中正与负方向在图9已标出,即正方向为轮前部俯下方向。
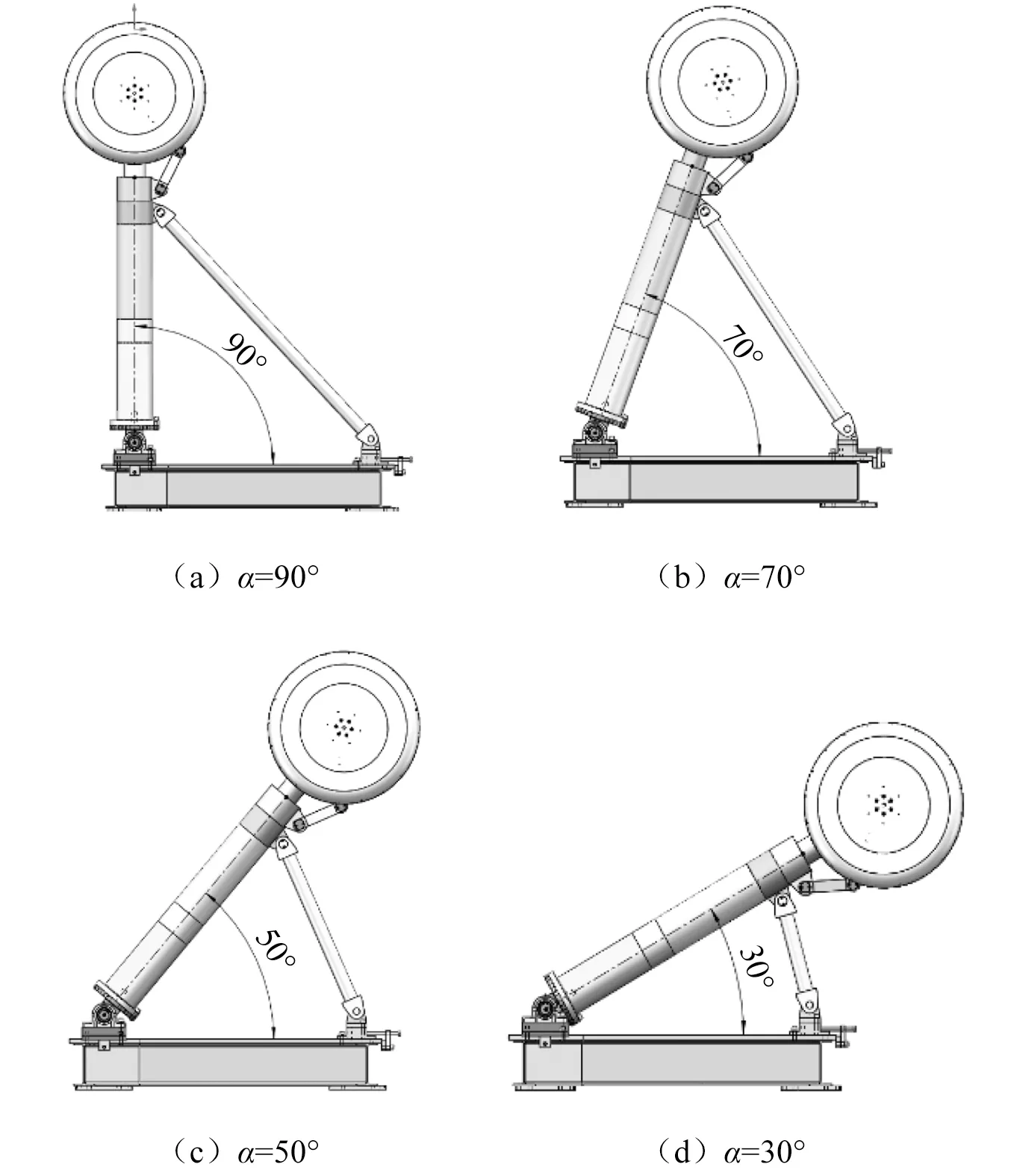
图7 不同攻角α起落架模型Fig.7 Models with different angles of attack α
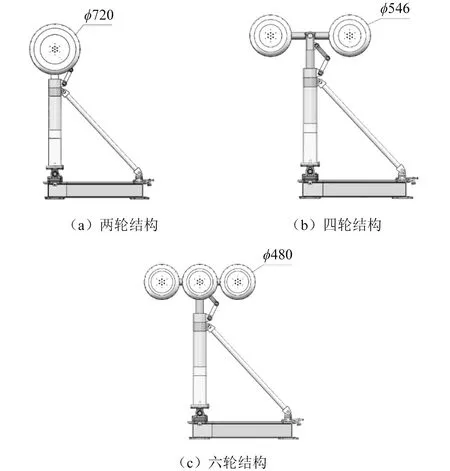
图8 试验不同轮数起落架模型(mm)Fig.8 Models with different wheel number(mm)
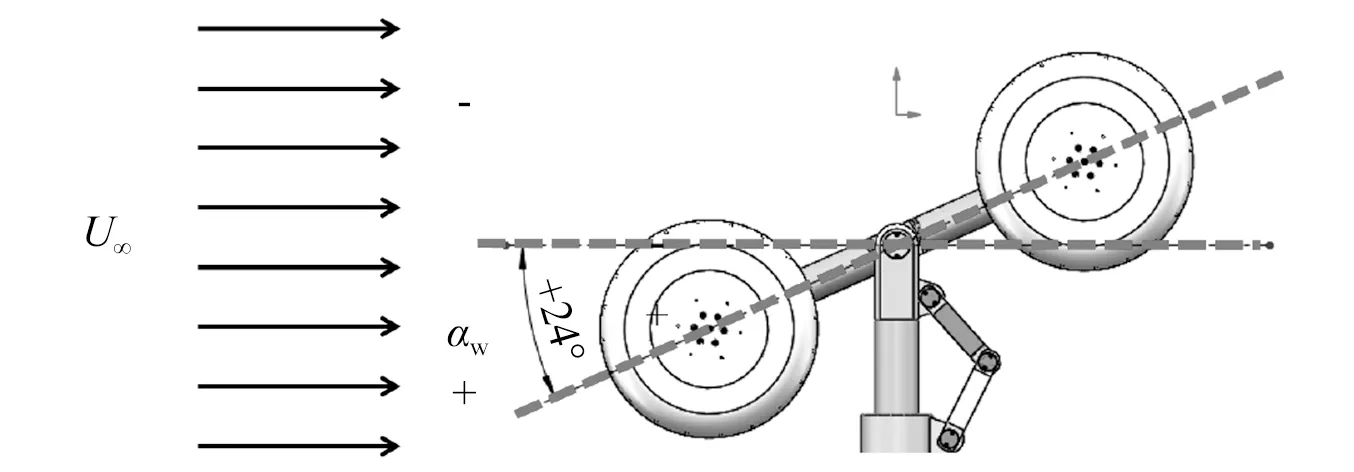
图9 轮攻角αw示意图Fig.9 Schematic of the wheel angles of attack αw
1.3.6 不同偏角β
飞机在起降过程中,常有侧向风存在,在与主流速度叠加后,会与起落架形成侧向夹角,即偏角。研究[20]认为,不同偏对起落架表面脉动压力具有一定影响。为评估其噪声影响,试验特别对两轮、四轮和六轮模型不同β状态下的噪声特性进行了分析,如图10所示,即β=0°,β=2°,β=4°,β=6°,β=8°。
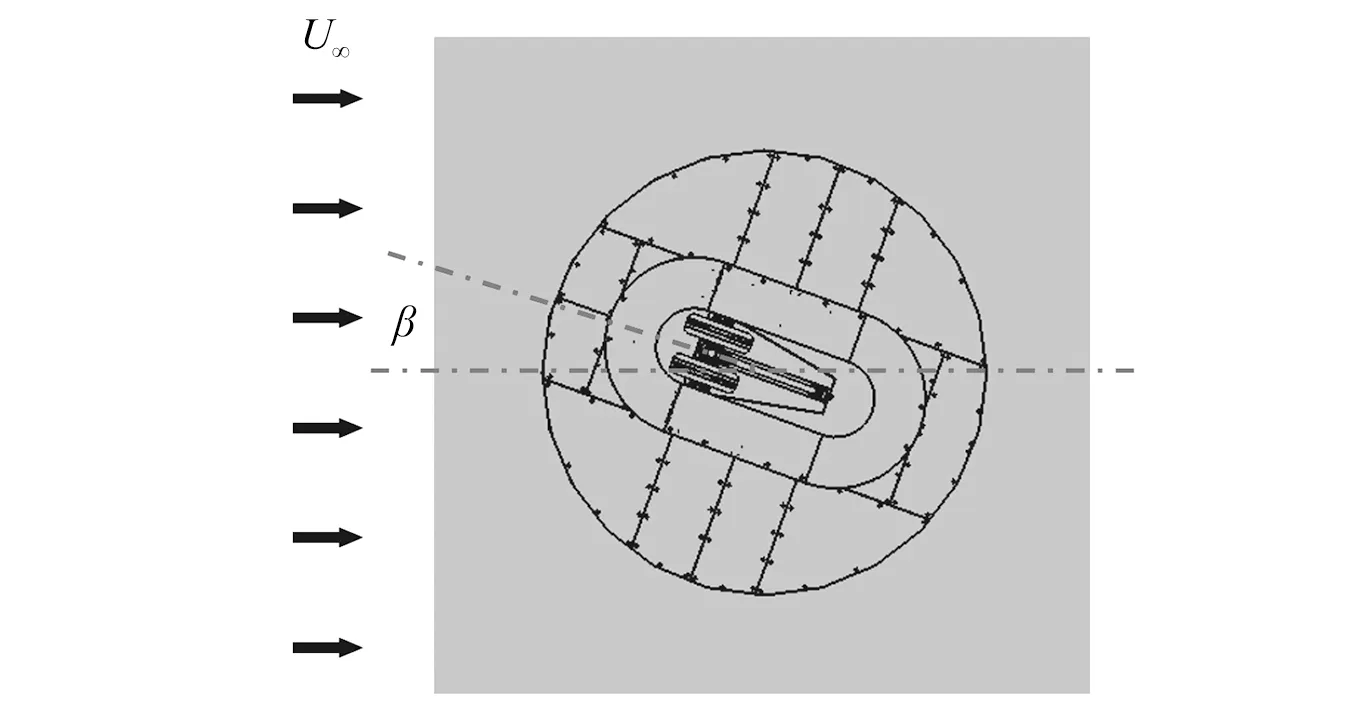
图10 偏角β示意图Fig.10 Schematic of the yaw attack β
1.3.7 轮部拆解
为配合其他参数研究,确定噪声源,试验中对轮部进行了拆解,具体结构将在后续讨论。
1.4 声学测试设备与数据处理方法
1.4.1 声学测试
试验采用自由场传声器与相位传声器阵列开展声学测试,同步实现噪声传播特性和噪声源分布规律分析,其总体布置如图11所示。
自由场传声器布置在模型侧面,配套支撑系统排架采用常规杆式结构,距离风洞中心6 m。支撑杆外敷设一层吸声衬,降低声反射对测量结果影响。试验选用G.R.A.S公司的1/2英寸传声器46 AE,频率范围为3.15 Hz~20 kHz,共布置30个自由场传声器,分为三排,各个编号,如图11所示。
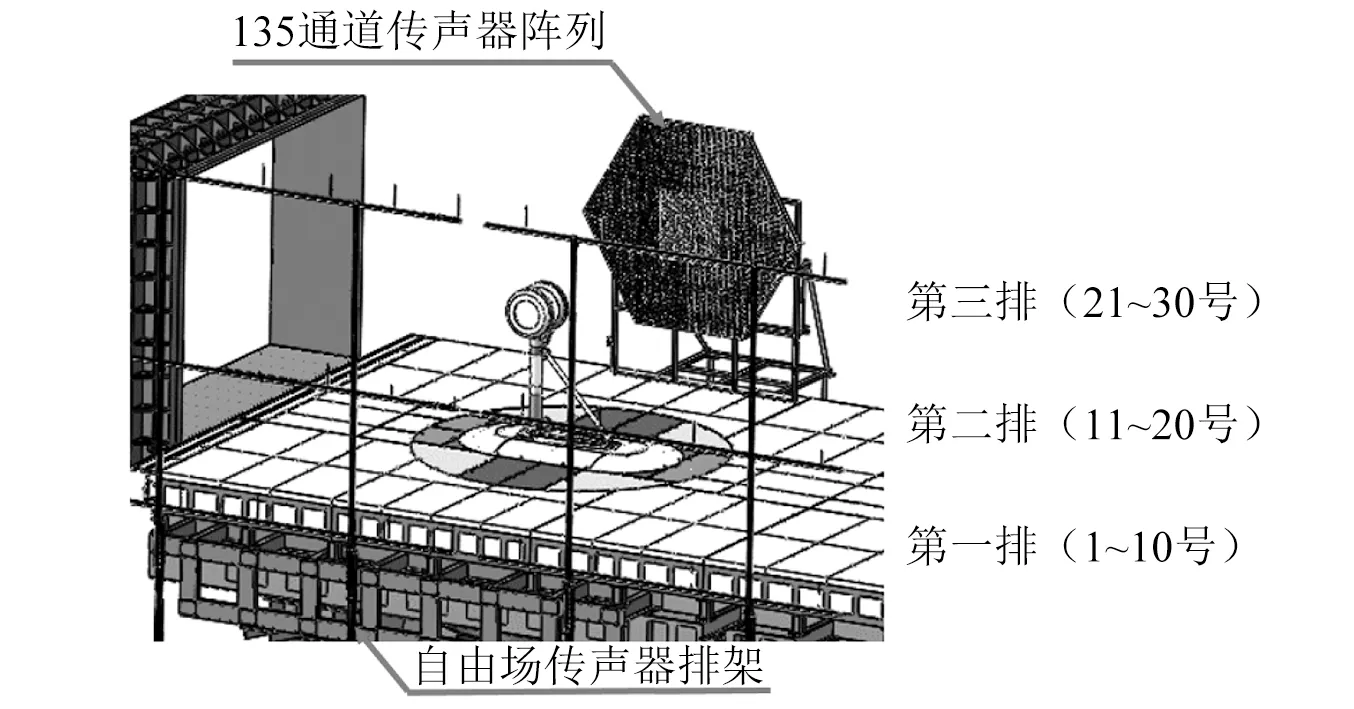
图11 声学测试布置图Fig.11 Set-up of the acoustic measurement
相位传声器阵列共135通道,采用G.R.A.S公司的40 PH,频率范围为100 Hz~20 kHz。为方便阵列架上传声器布置,阵列架设计成等间距网格。除网格部分外,阵列架其余部分包裹消声材料。阵列距离扫描平面中心为5.14 m,其相对位置如图12所示。

图12 阵列与起落架模型相对位置Fig.12 Relative position of the microphone array and the model
数据采集频率为51.2 kHz,自由场传声器与阵列采样时间分别为30 s和10 s。
1.4.2 CLEAN-SC噪声源定位方法
当前,基于波束形成(beamforming)技术的噪声源定位方法被广泛应用在声学风洞测量中,其核心是“延时求和”(delay-and-sum),能很好地清除低频回响噪声,得到声源分布图,在目前声学风洞和外场型号声学试验中得到广泛应用。波束形成基本表达式为[21]
(1)
式中:xi为扫表平面内第i个扫描点pi位置向量;Bi与h分别为该扫描点输出功率和指向向量;G为阵列传声器的互谱矩阵;M为阵列传声器数量,除以M2-M是为了将阵列输出功率谱转化到单一麦克风的量级,并扣除源自风洞背景噪声带来的对角线元素干扰。
传统波束形成算法得到的声源数据中包含有较高声源旁瓣,这些声源旁瓣容易被误认为声源,而且还有可能掩盖一些强度相对较小的真实声源。另外,该算法对于较低频率的声源空间分辨率差,有背景噪声影响时试验的信噪比也较低[22-23]。因此,基于传统波束形成学者相继提出DAMAS,CLEAN-PSF反卷积等先进算法,用以提高噪声定位能力。Sijtsma[24]提出了一种基于空间相干声源(spatial source coherence)的扩展CLEAN-SC算法,对飞行器机体噪声的测试结果更为合理,在阵列动态范围和分辨率上相对于CLEAN-PSF算法又有了显著的提高,具体见文献。本文采用CLEAN-SC作为噪声源定位的数据处理方法。
1.4.3 阵列数据声源区域积分
通过CLEAN-SC算法得到噪声源的声压云图后,可针对代表不同声源的特定区域范围进行积分,进而得到相应阵列数据的区域积分结果(source region integration,SRI)。本文运用区域积分结果分析各声源对总噪声贡献随频率的变化关系。具体步骤如下:首先将噪声源声压云图划分几个区域,第n个区域表示为Rn,其内部所有扫描点即表示为集合{pi|pi∈Rn}。利用点声源相加公式,即可得到
(2)

2 试验内容
为实现研究目标,本文采用试验矩阵方式对试验内容进行具体安排,如表1所示。表1中:每个模型状态分配一个序号用以区别;序号BG代表背景噪声测试,即3/4开口试验段表面为空,不安装任何模型。高度h,轮直径φ每个状态共有5个风速,分别为34 m/s,44 m/s,55 m/s,65 m/s和75 m/s。
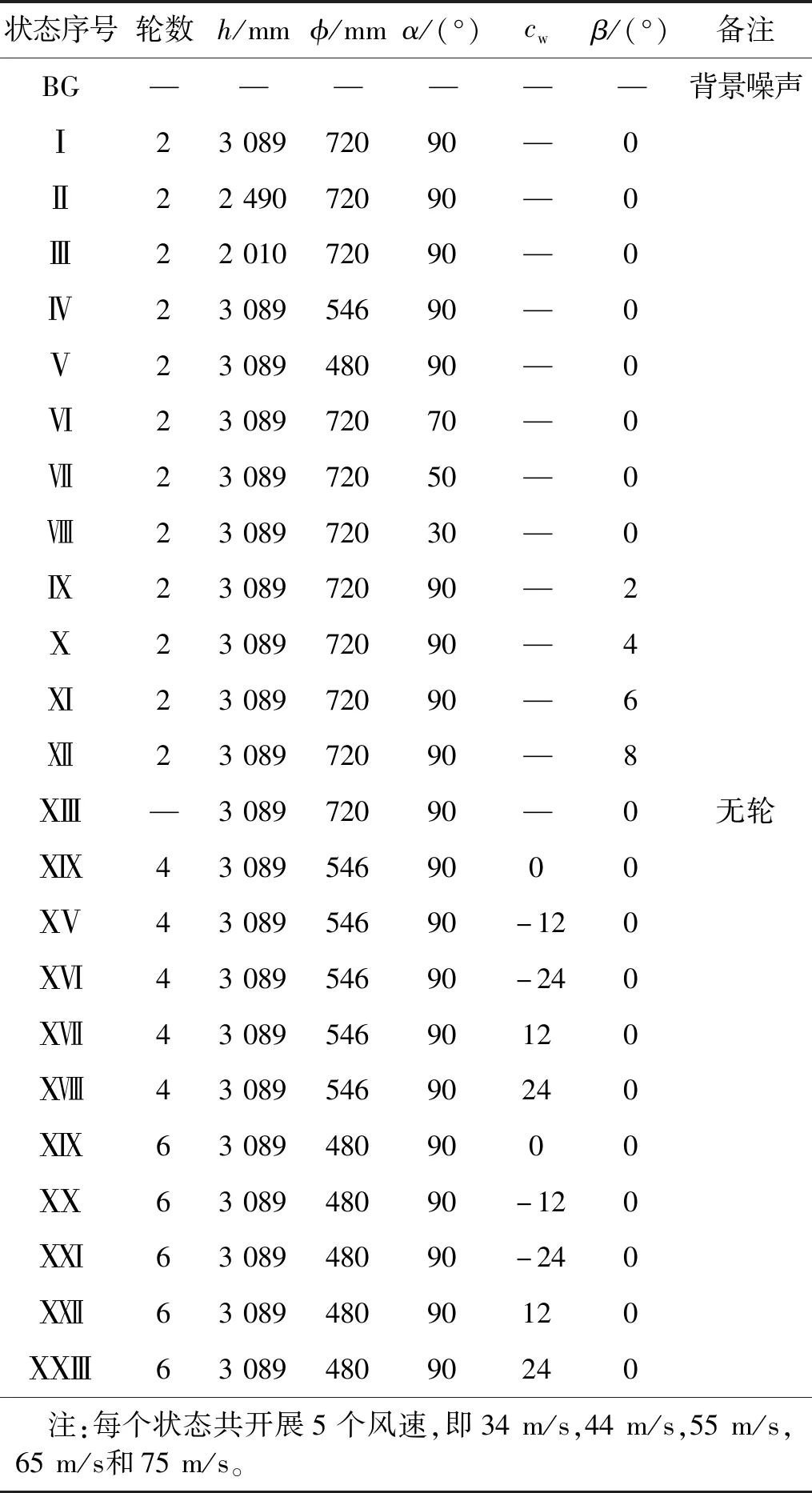
表1 试验矩阵Tab.1 Test matrix
3 试验结果与分析
3.1 背景噪声
背景噪声水平直接决定试验质量,为此试验特安排相关噪声测试。图13给出了在75 m/s风速下状态Ⅰ和背景噪声频谱对比。此处频谱分析采用8 192长度数据块,50%重叠并加Hanning窗。由图13可知,100 Hz~10 kHz分析频率范围内,状态Ⅰ噪声均高于背景噪声3 dB以上,具有较好信噪比,可用于后续数据分析。
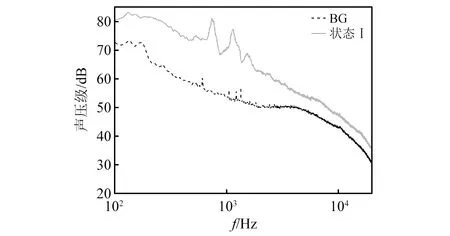
图13 75 m/s风速下状态I与背景噪声声压级频谱对比(15号传声器)Fig.13 Comparison of SPL spectra between scenario No.1 and background noise with 75 m/s (Mic.15)
3.2 不同风速的影响
风速对起落架噪声影响明显,本文针对状态Ⅰ进行了相关分析。图14是不同风速下状态Ⅰ声压级频谱对比,可以看出随着风速不断提高,声压级显著上升,且频谱中存在明显纯音峰值。
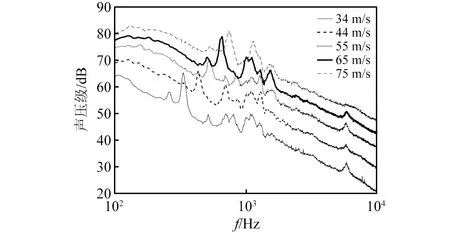
图14 不同风速下状态Ⅰ声压级频谱对比(15号传声器)Fig.14 Comparison of baseline test SPL spectra with different incoming flow speed acquired by Mic.15
纯音噪声可分为两类:第一类频率随风速显著变化,与斯特劳哈尔数成正比,由钝体扰流(流动分离/涡脱落)或空腔自激振荡产生[25];第二类峰值频率随风速变化不明显,与亥姆霍兹数成正比,产生原因主要为空腔中形成驻波产生的声共振、亥姆霍兹共振腔等[26-27]。图14中:200 Hz~800 Hz内各风速下峰值频率明显随风速变化,即第一类纯音;而在1 100 Hz,5 788 Hz频率附近即有与风速变化不明显的峰值,即第二类纯音。
3.2.1 噪声源位置
图15给出75 m/s风速下不同频率噪声源声压云图。由图15可知,234 Hz时主要声源为支杆,随着频率上升至387 Hz与489 Hz,噪声源不断向高处移动到扭矩连杆、支杆与外筒连接处。由图14可知710 Hz频率下纯音判断属于第一类范畴,声压云图显示其噪声源位置判断与轮部紧密相关。除底部连接轴外,大于2 068 Hz后噪声源基本集中于扭矩连杆、轮部。如图16所示,扭矩连杆虽然为一小尺度部件,但由于其在真实起落架中需要实现关键力学功能,因此拓扑结构复杂,包含多个钝体、空腔等几何构型,因此易产生大量噪声。底部连接轴判断是由于该处存在缝隙,进而产生空腔引起相关纯音噪声。因此,在真实起落架设计过程中,连接处应尽力避免产生类似缝隙。
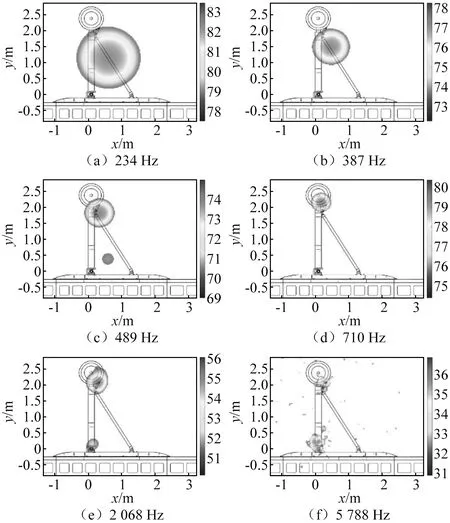
图15 状态Ⅰ不同频率噪声源声压云图(75 m/s)Fig.15 Noise source localization at different frequencies of scenario Ⅰ (75m/s)
3.2.2 部件贡献
为分析各部件声源对起落架总噪声的贡献随频率变化的关系,本文采用阵列数据区域积分,如1.4节所述。图17给出了阵列云图积分区域划分,其中区域A、B、C、D、E分别对应轮部、小尺度部件(含可视区域内扭矩连杆和支杆连接轴)、支杆、支柱连接轴、支柱。此外,区域“总积分”代表整个起落架模型。阵列数据区域积分频率范围为1 kHz~7 kHz,其中每25 Hz进行一次CLEAN-SC计算。

图16 扭矩连杆Fig.16 Torque link
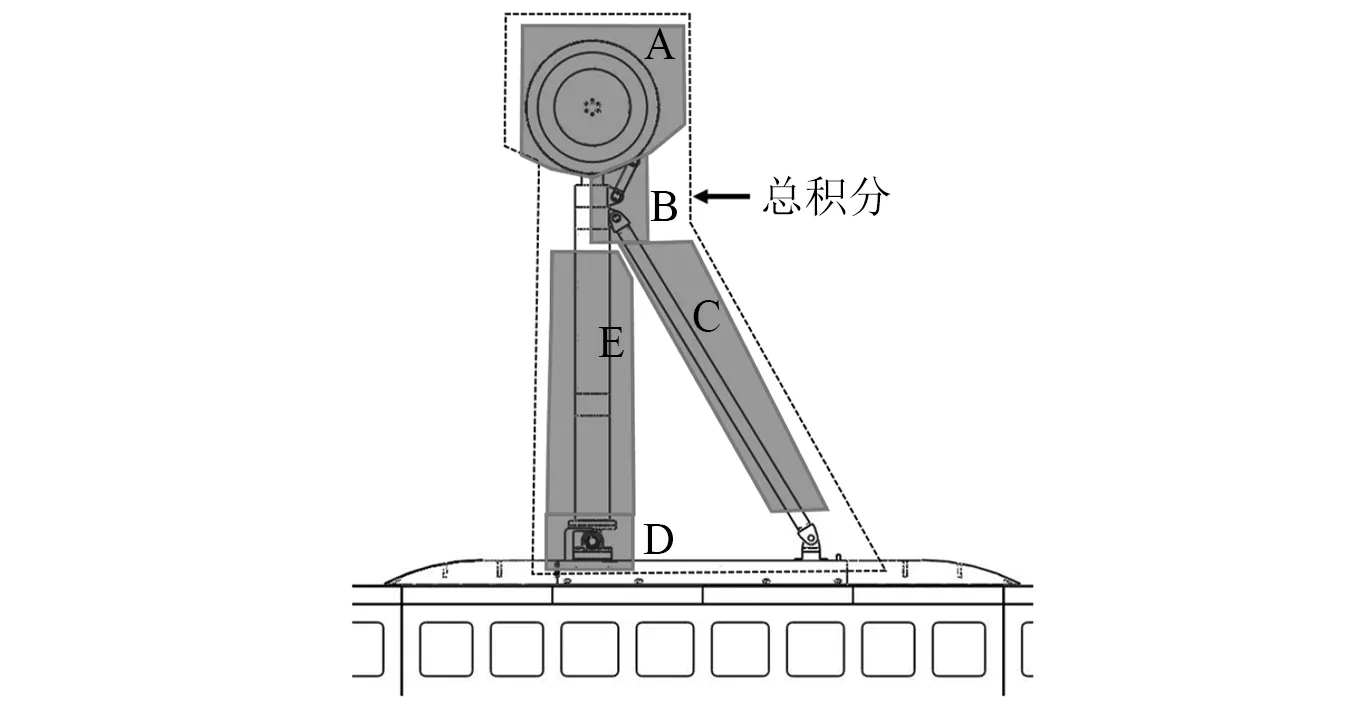
图17 声源区域划分Fig.17 Source region partitions
图18为不同风速范围内声源区域积分结果,可以看出,各风速下区域积分谱线趋势基本一致。以65 m/s风速为例,首先可以看出,除去总积分外,轮部(区域A)在高于4 050 Hz频率范围内声源积分最高,判断为主要噪声源。在600 Hz~700 Hz内总积分可观察到一个峰值,且该峰值频率与风速相关,属于第一类纯音噪声。由此可以判断,该峰值与图14中相应频率范围内第一类纯音噪声对应。由于区域A积分也有该峰值且声压级非常接近,说明该第一类纯音基本源于轮部。区域B在400 Hz~1 300 Hz内声压级值仅低于总积分与区域A,说明该频率范围内小尺度部件对起落架总噪声贡献大。区域C在低于400 Hz范围内除总积分外排声压级最高,说明支杆在低频率范围内是最大贡献部件,甚至高于轮部。但是,随着频率升高,支杆对总噪声贡献显著下降。区域D贡献始终靠后,说明其对总噪声贡献较低。值得注意的是,支柱虽然是最大部件,但是其对应区域E对总噪声贡献并不总是最大。在450 Hz以下仅低于支杆,但随着频率升高,其贡献进一步下降,低于轮部与小尺度部件,在2 025 Hz后,又有一定升高,仅低于轮部。
由以上讨论可知,起落架各个部件对总噪声的贡献随频率发生变化,且各部件对总噪声的贡献并非与其尺度成正相关。总体而言,轮部为最主要噪声源,支杆与支柱主要产生低频噪声,且支杆大于支柱。小尺度部件的虽然体积小,但对噪声贡献不容忽视。
3.2.3 指向性特征
起落架噪声具有指向性特征,为此本文选取第二排3个传声器所得数据进行分析,分别为图11所示第12号、15号和19号传声器,其相对位置如图19所示。由于3个传声器距离声源距离不同,此处分析只关注各自频谱内相对量的显著差异。

图19 用于指向性影响分析的3个传声器位置对比Fig.19 Comparison of three microphones used for directivity analysis
图20给出了状态I 3个位置传声器声压级频谱对比(75 m/s风速)。由图20可知,频谱趋势基本一致,反映出指向性对宽频噪声特征影响相对较小,但是其对不同频率的纯音噪声测量差别较大。例如,位于744 Hz附近峰值,其噪声源位置如图21(a)所示为轮毂边缘,3个传声器均测量到其存在,仅幅值略有不同;相比而言,15号传声器测得位于1 152 Hz峰值,如图21(b)所示声源为轮部边缘或扭矩连杆,但在12号和19号传声器频谱中不明显。
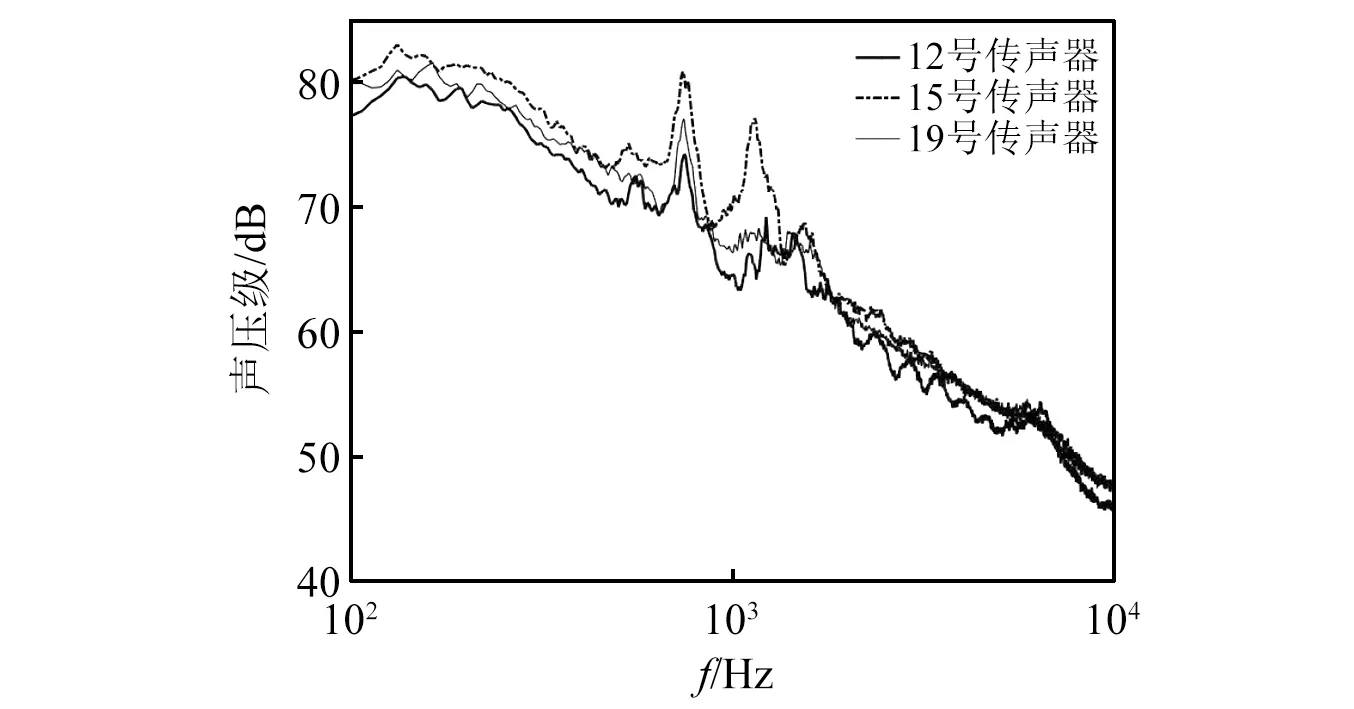
图20 3个位置传声器声压级频谱对比(75 m/s)Fig.20 Comparison of SPL spectra measured from three microphones with different positions (75 m/s)
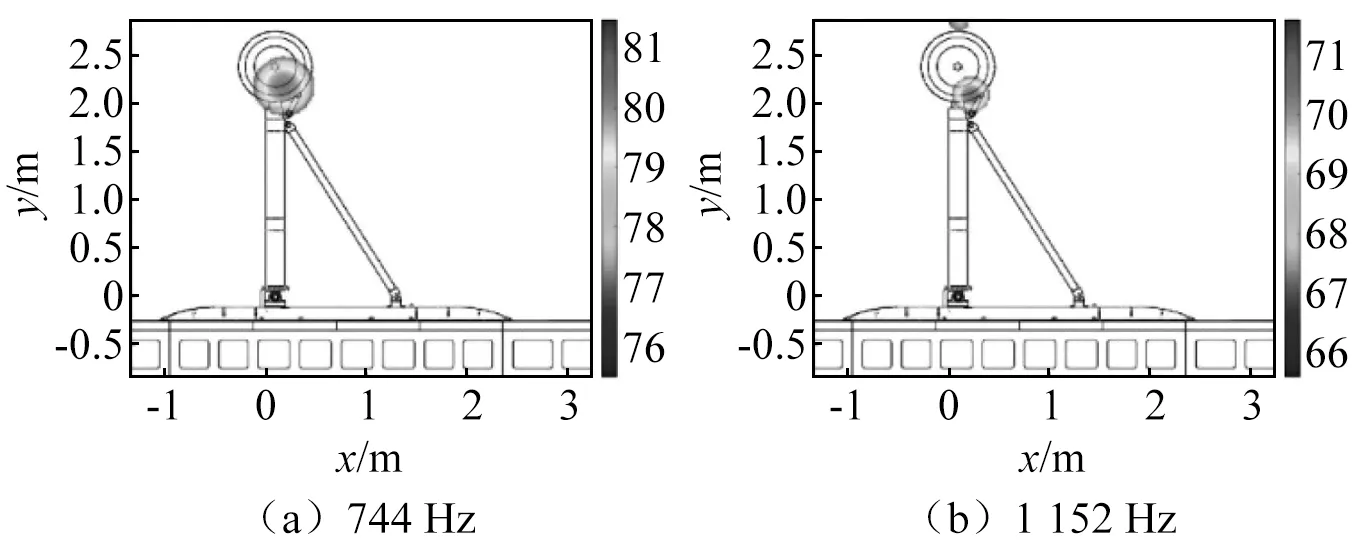
图21 744 Hz与1 152 Hz下噪声源声压云图Fig.21 Noise source localization at 744 Hz and 1 152 Hz
图22给出3个传声器测量总噪声声压级随风速变化,计算频率范围为100 Hz~10 kHz,其中具体数值也相应给出(由上到下分别来自15号、12号、19号测量结果)。由于15号传声器距离声源起落架较近,其测量结果始终大于其他两个传声器。此外,位于上游的12号传声器在低风速时大于位于下游的19号传声器,而高风速时小于19号。由此可知,随风速变化,总声压级增长率与指向性相关。
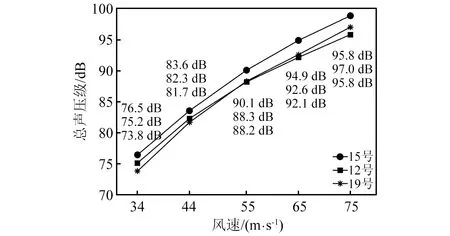
图22 3个位置传声器总声压级随风速变化(计算频率范围100 Hz~10 kHz)Fig.22 OASPL of three microphone positions with different flow speed(frequency range 100 Hz~10 kHz)
3.2.4 归一化频谱
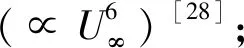
(3)
式中:Uref为参考风速,本文采用75 m/s;n为幂次,6次方律即n=6,n=7次方即n=7。
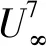
对于纯音噪声,由图23(b)可知,第一类纯音由于频率改变无法重合。第二类纯音由于产生原因特殊,幅值并未有明显n次方规律。
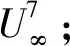

图23 不同风速频谱归一化结果(15号传声器,参考速度75 m/s)Fig.23 Results of normalized spectra with different incoming flow speed(Acquired by Mic.15,reference flow speed 75 m/s)
3.3 不同高度的影响
起落架设计需要根据需求选取不同高度,其对噪声特性也将产生影响,为此本文进行了试验分析。如1.3节所述,试验共采用3种高度模型,分别为h=2 010 mm,2 490 mm和3 089 mm,即表1中状态Ⅰ~Ⅲ。图24给出了三种高度条件下的频谱对比图,由图24可知,高频段(>2 000 Hz)3个频谱差别较小;在低频段(<600 Hz)宽频噪声幅值差别较大。此外,由3.2节讨论中已知,由轮部产生的第一类纯音幅值也发生了一定变化。已知轮部结构未改变,幅值变化推测是由于高度变化,轮部位置与15号传声器相对位置发生改变,进而由于指向性影响造成的。
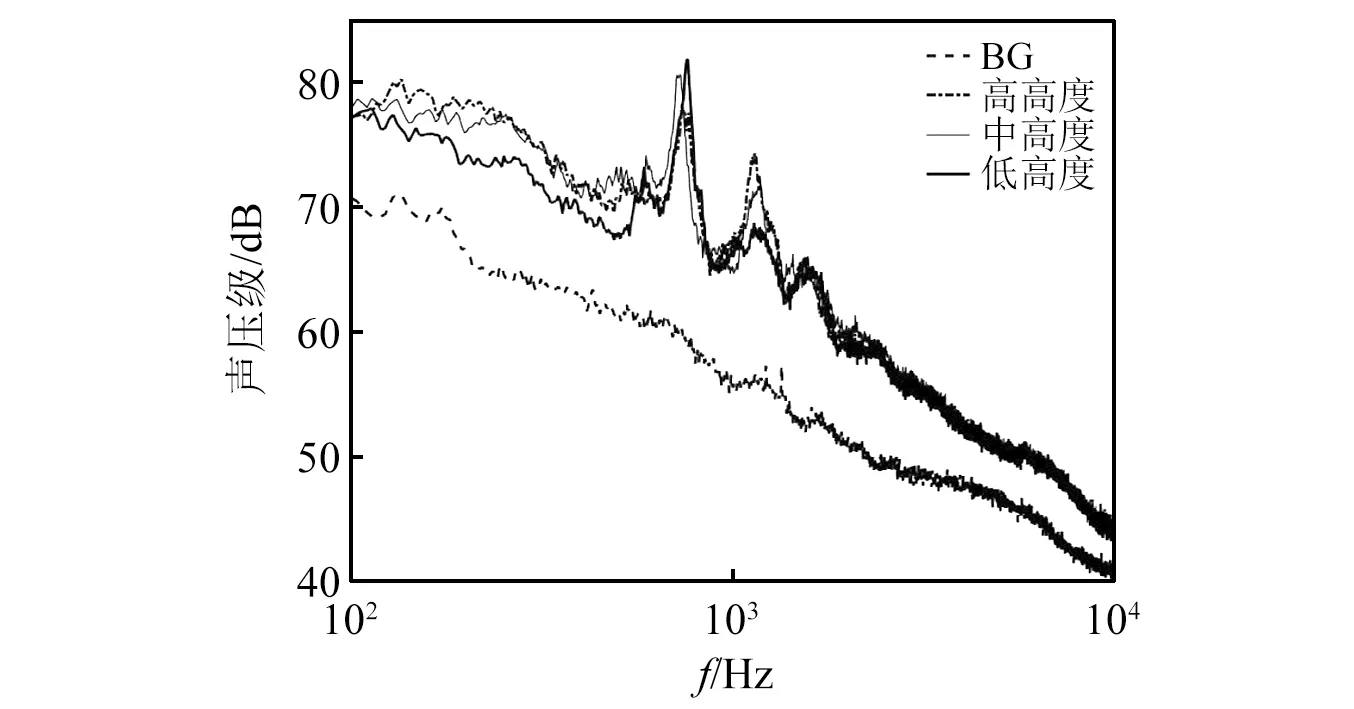
图24 不同高度状态声压级频谱对比(15号传声器)Fig.24 Comparison of SPL spectra with different h acquired by Mic.15
图25给出了三种高度状态下在低频段典型频率(200 Hz)的噪声源定位结果。可以看出,低频段噪声源变化主要发生在支杆,这主要是因为随着模型高度变化,支杆长度与角度也随之调整,进而产生不同噪声特征。
3.4 不同轮直径的影响
由3.2节讨论可知,轮部是重要噪声源之一。因此,其关键参数—直径φ对整个起落架噪声有重要影响。为此,本文对不同φ的噪声特性进行了分析。
图26给出了三种轮直径状态下噪声频谱。由图26可知,总趋势变化并不明显,即φ对宽频噪声特性影响较小。然而,对于与轮部相关纯音特征影响较大。例如,大轮状态下峰值在750 Hz附近的一纯音频率在中轮与小轮状态下明显前移。此外,小轮状态下出现若干不明原因尖峰,频率为443 Hz,887 Hz和1 331 Hz,具有一定谐波特征。为研究噪声源,本文采用拆解方法将轮部卸下,即状态ⅩⅢ,如图27所示。
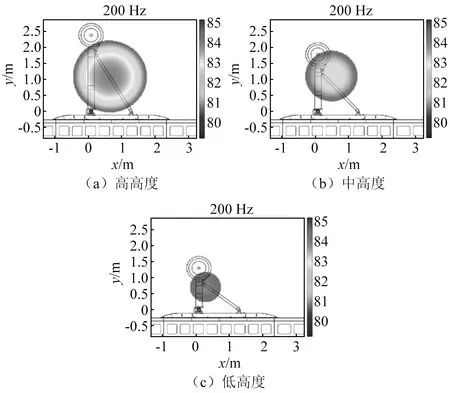
图25 200 Hz下不同高度状态噪声源声压云图Fig.25 Localization of sources at 200 Hz with different height
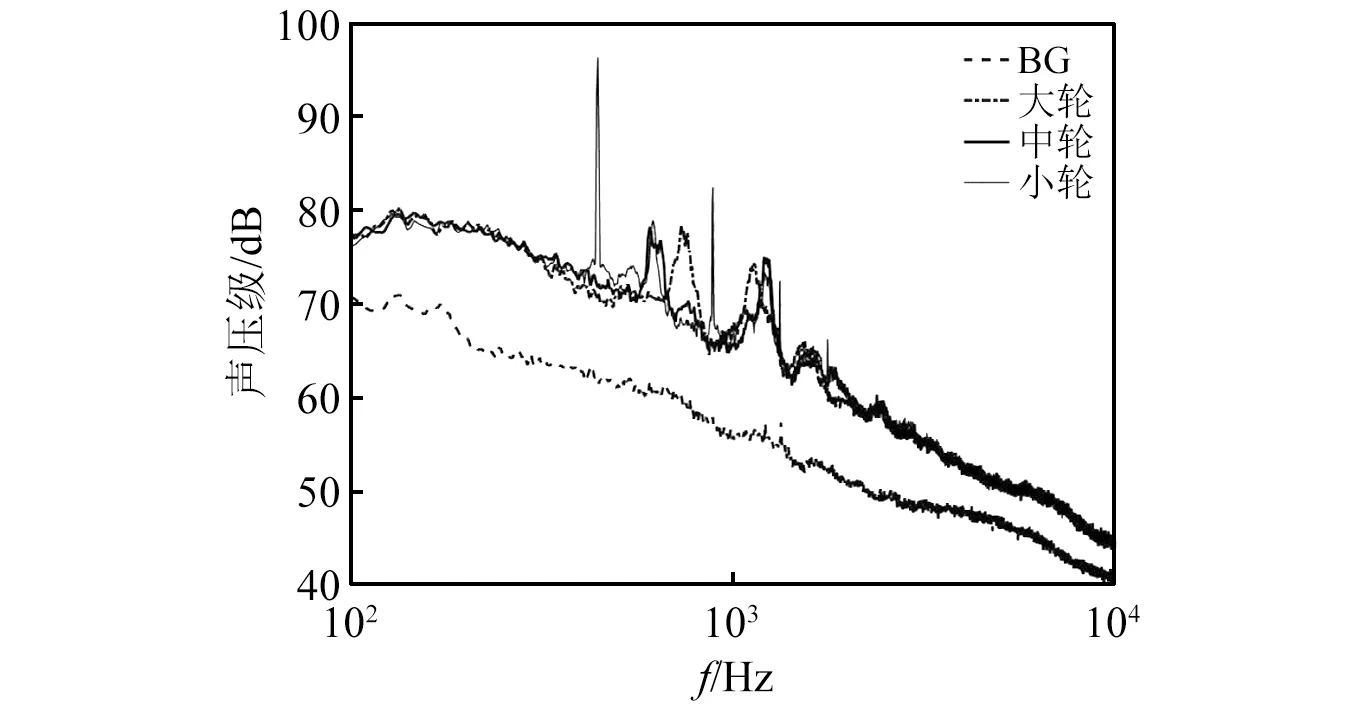
图26 不同轮直径起落架噪声频谱特性(15号传声器)Fig.26 Spectra of landing gear with different wheel diameter(Mic.15)

图27 无轮状态(状态ⅩⅢ)Fig.27 No-wheel scenario (scenario ⅩⅢ)
图28给出了小轮状态和无轮状态频谱对比,可以看出不明峰值在两种状态下依然存在,仅幅值发生一定变化,判断该噪声源与轮部无关。图29给出了443 Hz时无轮状态噪声源定位结果,发现噪声源出现在顶部连接轴端点,是来流吹击顶部引起的钝体扰流纯音噪声。
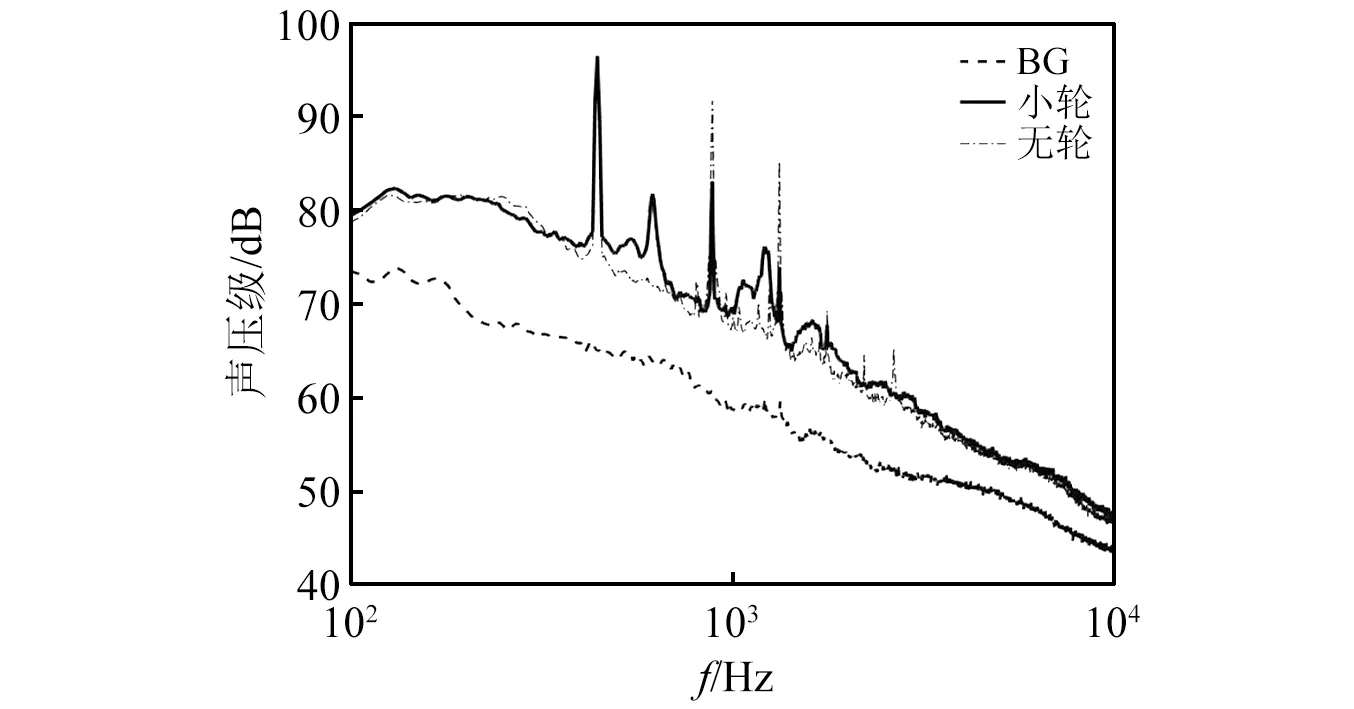
图28 小轮与无轮状态下频谱对比(15号传声器)Fig.28 Spectra of the small wheel and no-wheel spectra(Mic.15)
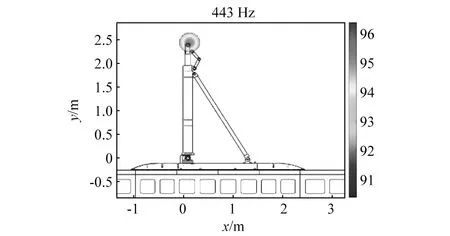
图29 无轮状态下不同频率噪声源CLEAN-SC定位结果Fig.29 Noise source localization of no-wheel scenario at different frequencies in CLEAN-SC
顶部端点纯音噪声仅在小轮状态出现,判断是由于随着轮直径变小,原先暴露在轮部侧面尾流的顶部端点转变为直接暴露在来流中,因此产生与无轮状态相似的单频纯音噪声。所以,在进行轮部尺寸设计时,应综合考虑两侧轮间端点噪声情况;为避免增加纯音噪声,轮部直径不能过小。
3.5 不同攻角的影响
飞机在起降过程中需要收放起落架,该动态过程会引起起落架攻角不断变化,对噪声特性也会产生一定影响。图30给出了起落架不同攻角状态下噪声频谱对比,其对应构型在1.3节中已经具体描述。由图30可知,攻角变化引起的噪声频谱特征区别明显。首先,宽频噪声随着攻角显著变化,如α=30°整个频段总体低于其他攻角;第二,纯音特征变化更为突出,例如α=90°时在744 Hz附近出现的纯音在α=70°时向左移动,在α=50°继续移动且幅值大幅减小,而在α=30°基本消失,相似情况在α=90°时的1 141 Hz频率附近纯音也有出现,其他攻角下该峰值基本消失;第三,α=70°和α=50°时3 616 Hz出现一异常尖峰。图31给出了该频率下起落架攻角为70°时噪声源定位结果,发现该噪声源出现在底部连接处。这是由于随着起落架倒伏,连接处出现缝隙,形成典型空腔噪声。随着攻角继续变化,倒伏幅度增长后缝隙消失,因此该峰值不再存在。
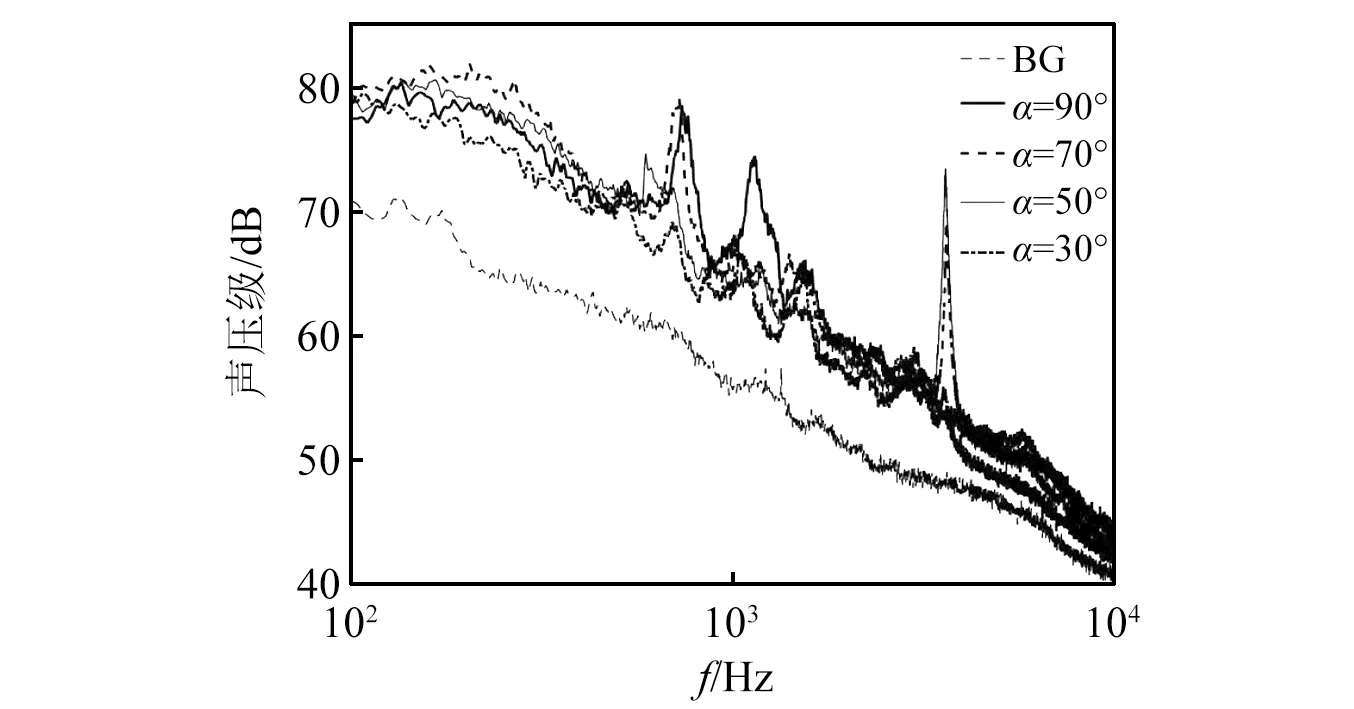
图30 起落架不同攻角噪声频谱对比(15号传声器)Fig.30 Spectra of the landing gear with different angles of attack(Mic.15)
由上所述可知,攻角变化对宽频与纯音噪声均有显著影响。此外,一些原本重要声源部件可能不再产生过高噪声;而另一些部件却成为显著声源,这些情况在起落架噪声设计中均需要考虑。
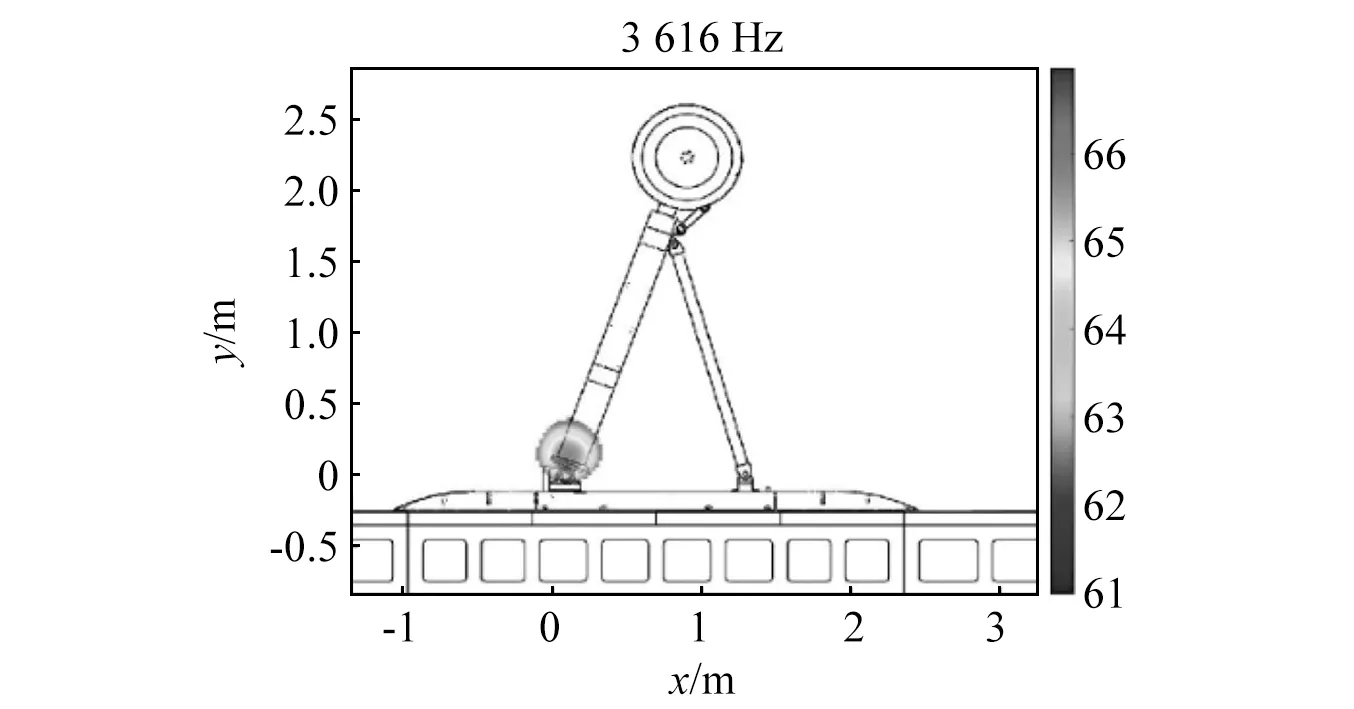
图31 起落架攻角为70°时声源声压云图Fig.31 Noise source localization of the landing gear at α=70°
3.6 不同轮数的影响
当前,起落架构型主要以两轮、四轮与六轮为主。为研究轮数对起落架噪声带来的影响,具体模型细节如1.3节所示。
图32为75 m/s风速下两轮、四轮与六轮起落架噪声频谱对比。由图32可知,总体而言对比两轮结构,四轮与六轮结构曲线较为平缓,纯音幅值较低。这些纯音在3.2节讨论中已经确定产生与轮部有关,该现象说明增加轮数有助于抑制轮部纯音噪声。
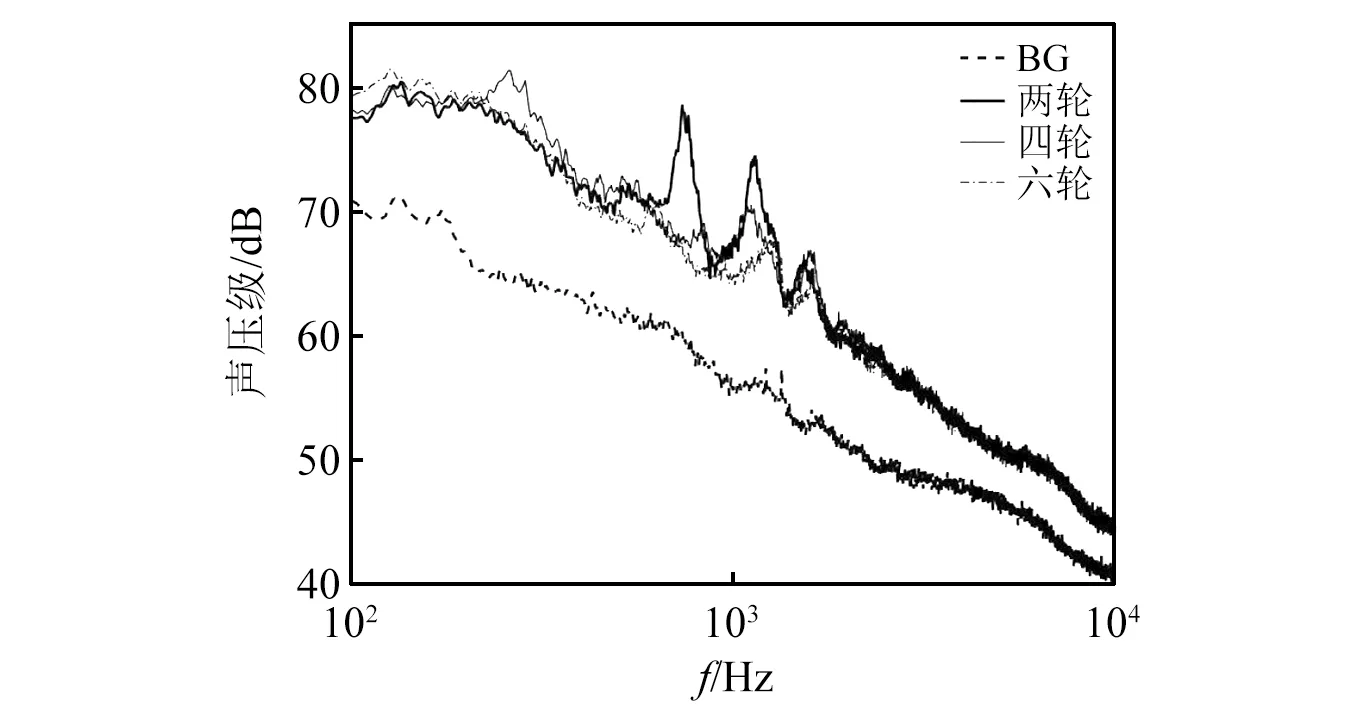
图32 75 m/s风速下两轮、四轮与六轮起落架噪声频谱对比(15号传声器)Fig.32 Comparison of two-wheel,four-wheel and six wheel landing spectra under 75 m/s(Mic.15)
图33与图34分别给出了四轮与六轮结构起落架在不同风速条件下的声压级频谱对比。通过与图14比较,再次验证了曲线较为平缓这一结论。图35与图36给出了四轮与六轮起落架模型基于CLEAN-SC的典型噪声源分布。对于四轮起落架,轮轴架梁与减震支柱(内筒)连接处成为一个明显噪声源。对于六轮起落架,连接杆前部,即前轮和中轮之间也存在明显声源。
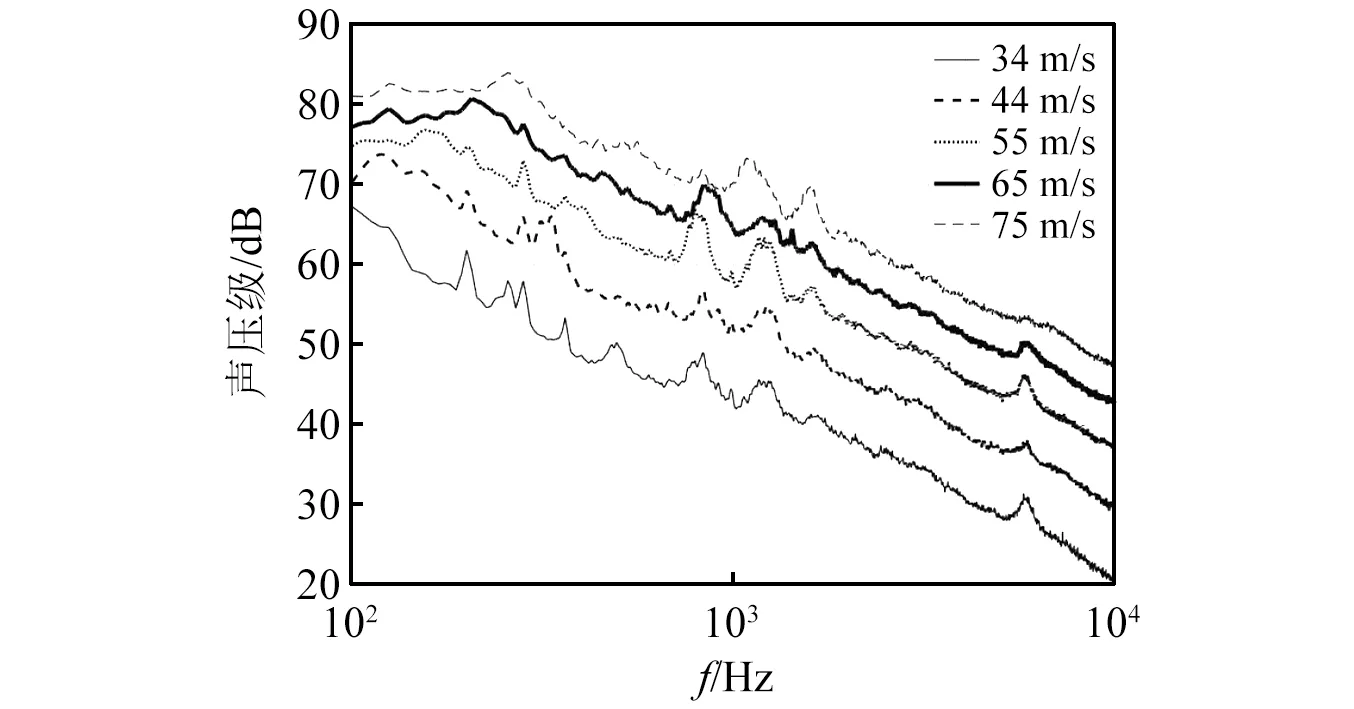
图33 不同风速下四轮起落架噪声频谱对比(15号传声器)Fig.33 Comparison of four-wheel landing gear spectra(Mic.15)
综上,与两轮结构比较,四轮与六轮曲线较为平缓,轮部引起的纯音噪声大幅度下降。同时,由于增加了连接杆,成为四轮与六轮结构的一个重要声源。
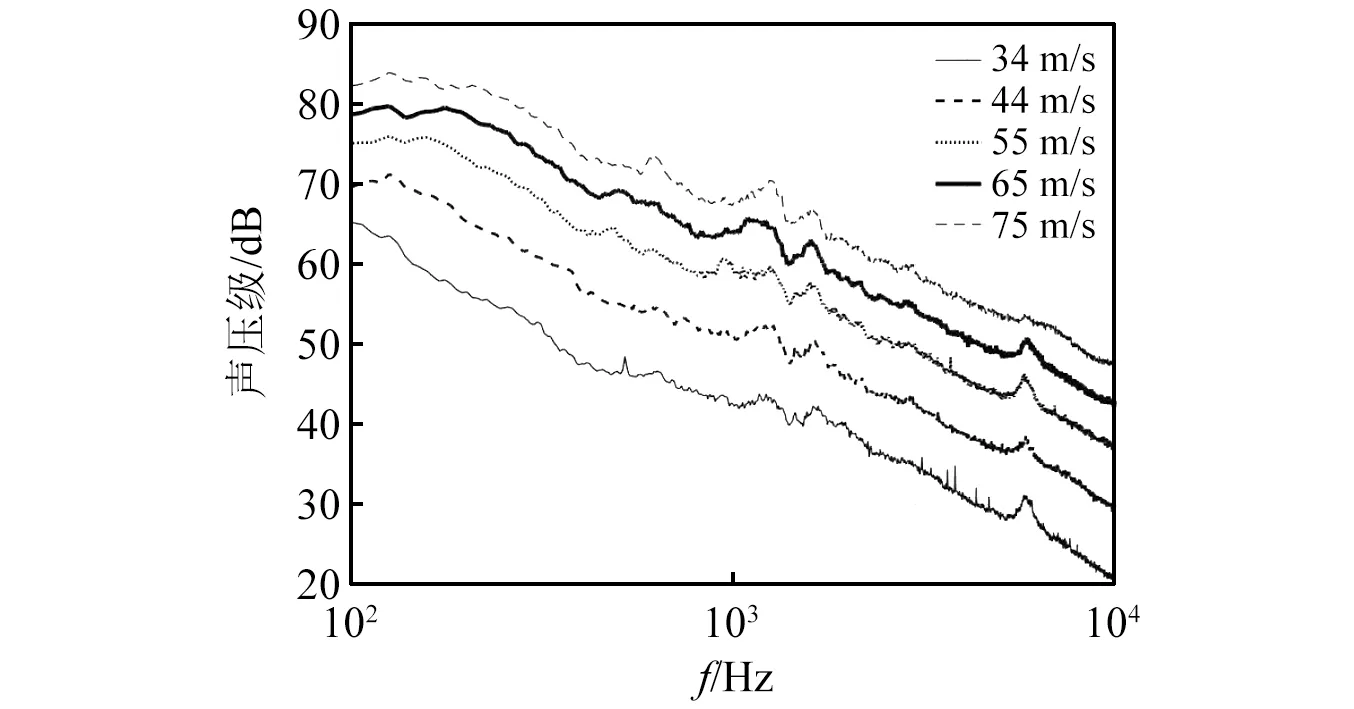
图34 不同风速下六轮起落架噪声频谱对比(15号传声器)Fig.34 Comparison of six-wheel landing gear spectra (Mic.15)
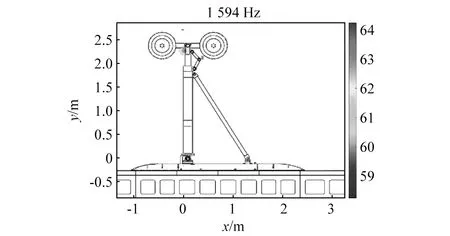
图35 四轮起落架声源声压云图定位结果Fig.35 Noise localization of four-wheel landing gear
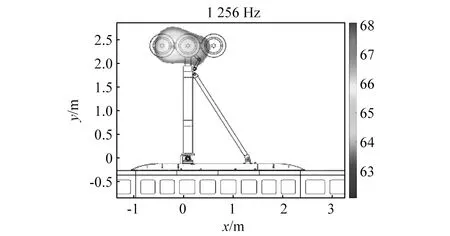
图36 六轮起落架声源声压云图定位结果Fig.36 Noise localization of six-wheel landing gear
3.7 不同轮攻角的影响
如1.3节所述,在四轮与六轮起落架收放过程中,轮攻角会根据姿态进行调整,进而影响噪声特征。初步判断,轮攻角αw变化对减震支柱与支杆噪声特征影响较小,但对与轮部相关结构噪声影响较大。
图37与图38给出了不同轮攻角状态下四轮与六轮起落架噪声频谱对比。可以看出,发生变化的主要为纯音特征。由图中纯音部分放大图可知,对于四轮起落架,在500 Hz~900 Hz,1 000 Hz~2 000 Hz频率范围内,随着轮攻角变化,峰值幅值和频率都有所改变;而对于六轮起落架,相似现象出现在500 Hz~800 Hz和1 000 Hz~2 000 Hz频率范围。
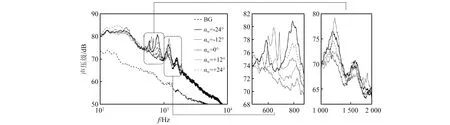
图37 四轮起落架不同轮攻角噪声频谱对比(15号传声器)Fig.37 Comparison of the four-wheel landing gear with different wheel angle of attack (Mic.15)

图38 六轮起落架不同轮攻角噪声频谱对比(15号传声器)Fig.38 Comparison of the six-wheel landing gear with different wheel angle of attack (Mic.15)
3.8 不同侧滑角的影响
如1.3.1节~1.3.6节所述,偏角产生是由于飞机起降过程中侧向风引起的,角度一般较小。为此,本文比较了β=0°,β=2°,β=4°,β=6°与β=8°时的噪声特征。图39给出了75 m/s风速下两轮、四轮与六轮起落架在不同偏角时的频谱对比。由图39可知,随着β改变,噪声频谱重合度较好,并未发生显著变化。因此可以推断,偏角对起落架噪声影响较小,设计过程中可以不予考虑。
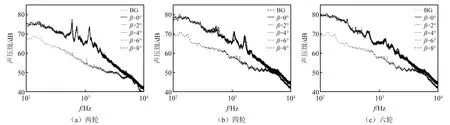
图39 起落架不同偏角状态下噪声频谱对比(15号传声器)Fig.39 Comparison of landing spectra with different yaw angles (Mic.15)
4 结 论
本文通过大尺度声学风洞试验研究,分析了不同结构参数对起落架噪声的影响规律。主要结论如下:
(1)本文通过声学风洞试验研究,分析了不同结构参数对起落架噪声的影响规律。试验研究发现,起落架各个部件对总噪声的贡献随频率发生变化,且各部件对总噪声的贡献并非与其尺度成正相关。
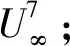
(3)起落架高度引起的噪声特征变化主要集中于较低频段,由随之发生变化的其他部件引起的。轮部直径不应过小,否则易使两侧轮中间部件直接暴露在来流中,增加纯音噪声。
(4)攻角变化对起落架噪声各类特征有显著影响,是低噪声设计中需要考虑的重要因素;8°范围内偏角对噪声特征影响较小,设计过程中可以不予考虑。
(5)相比两轮结构,四轮与六轮起落架噪声频谱纯音特征有所减弱,但增加的连接杆将成为重要声源之一;此外,四轮与六轮起落架轮攻角变化对频谱纯音特征有较大影响。
