基于PSO算法优化的RBF神经网络水厂混凝投药控制*

庹婧艺 徐冰峰 徐悦 喻岚 王雪颖 郭露遥

（昆明理工大学 建筑工程学院，昆明 650500）

0 引言

目前国内多数水厂投药量仍靠人为因素调节，如经验法、烧杯试验法等。本文数据来源于昆明市某自来水厂机器采集的源水浊度等实时数据。当出水余氯与浊度不够理想时，其水厂投药量通过当班工作人员人为调节，既耗人力又耗财力，且投药量仅靠个人经验的投药方式有很大的个人主观因素影响。其他学者就此类问题提出了许多预测出水浊度或投药量的方法，例如建立二元回归分析模型［1］、机理模型［2］、Elman ANN算法模型［3］、优化BP神经网络模型［4-5］等，通过数量间的映射关系，运用模拟分析掌握水厂混凝投药量的规律。但二元回归模型需要对高浊期与低浊期水质进行分类建立回归模型，对数据要求高且精度较差。机理模型建立难度大、求解困难，且对不同工艺水厂需要重新建模，适应性差。其他神经网络模型多数存在迭代次数高、鲁棒性差、易陷入局部极小值等问题。

PSO粒子群算法与RBF神经网络算法均属于近年的主流算法，PSO算法本身拥有优秀的全局搜索能力，每个粒子运动轨迹保持独立，仅接受全局适应度的约束，迭代次数较普通遗传算法快很多。RBF神经网络是简单的多层前馈神经网络，可以近似任意非线性函数，精度高，在模糊识别、非线性拟合中有着广泛应用。RBF神经网络与PSO粒子群算法结合后，具备了误差反馈调节能力，提升了算法的全局搜索性，拥有更高精度且降低了鲁棒性。本文数据选自昆明市某自来水厂，基于PSO算法优化后的RBF神经网络，利用敏感度分析水厂投药量影响因子，建立了4类源水参数与投药量之间的高维映射模型，以解析源水数据与投药量之间的规律，实现对投药量的动态预测。

1 理论基础

1.1 RBF神经网络原理

RBF的原理是使用核函数（cover函数）方法，将输入向量空间转换到隐层，使样本点逼近一个连续的高维度曲面，这样更容易求得插值曲面，使线性不可分问题变为可分。得到插值曲面后，将自来水厂非线性待求样本值映射到曲面，就能得到投药量模拟预测值。为了拟合大数据量，广义的RBF函数网络中心点数量与训练样本数量不一致［6］，由输入层、隐层、输出层组成。设输入值为Xk，则投药量输出值Y（x）为：

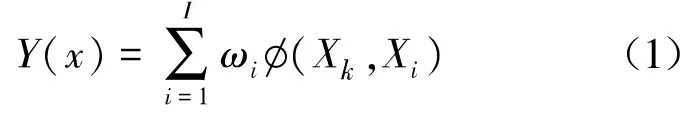
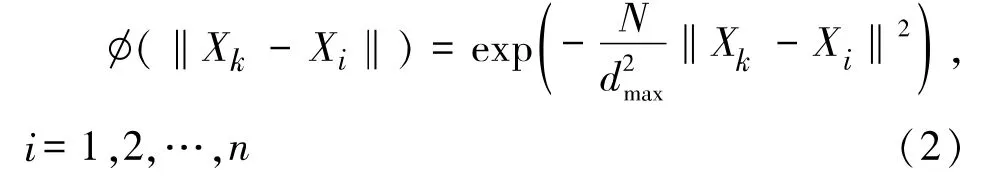
式中，n为隐层数，也是基函数中心点个数［7］；dmax为中心点Xi的最大距离。

RBF基函数模拟原理如图1所示，散点为待拟合的训练样本，X轴处相同函数是基函数，x1处样本点实值为a，基函数乘以权值后模拟出插值函数，RBF拟合的插值Y（x）就是b点与c点的纵坐标之和。在RBF网络中，需要训练的参数为：隐层中基函数的中心点位置；隐层节点个数N；隐层中基函数的标准差；隐层到输出层的函数权值。最终求得最优解，尽可能使虚线曲线拟合训练样本。

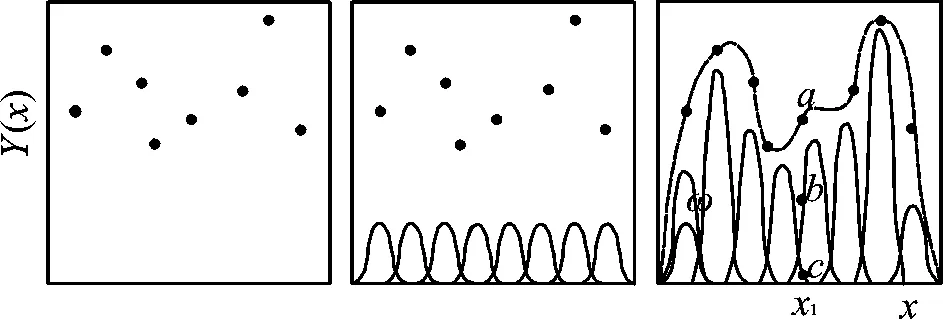
图1 RBF基函数模拟原理

1.2 PSO粒子群算法原理

PSO算法最早源于对鸟群进食的研究，基于种群智能行为的随机搜索算法，个体鸟类便是PSO算法中的粒子i，食物的位置便是问题的最优解。在D维搜索空间中，粒子的位置可由坐标xi=（xi1，xi2，…，xid）表示，运动速度可由向量vi=（vi1，vi2，…，vi）表示。鸟群在飞行进食时，每个个体都会记录飞行运动过程中的最优位置，即个体最佳点ibest；在每一次迭代运动后，个体也通过鸟群经验共享和飞行协作来更新最优进食点，即全局最佳点gbest，每一次粒子的飞行位置优劣和运动速度方向都由f（x）适应值函数约束，最终使种群在复杂的高维空间中获得最优解。PSO算法收敛速度相较于遗传算法更快，且具有更好的聚类效果，其飞行位置与运动速度由式（3）、式（4）决定：

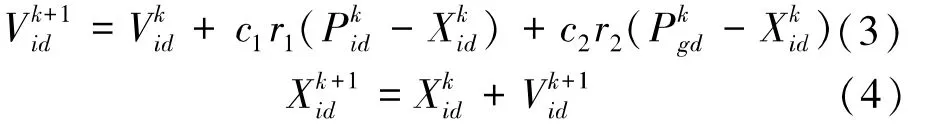
2 优化算法模型的建立

2.1 数据预处理

2.1.1 影响因子确定

本文采用全局敏感度分析法，计算昆明市某自来水厂7个源水影响因子与投药量之间的敏感度系数，结果如表1所示。

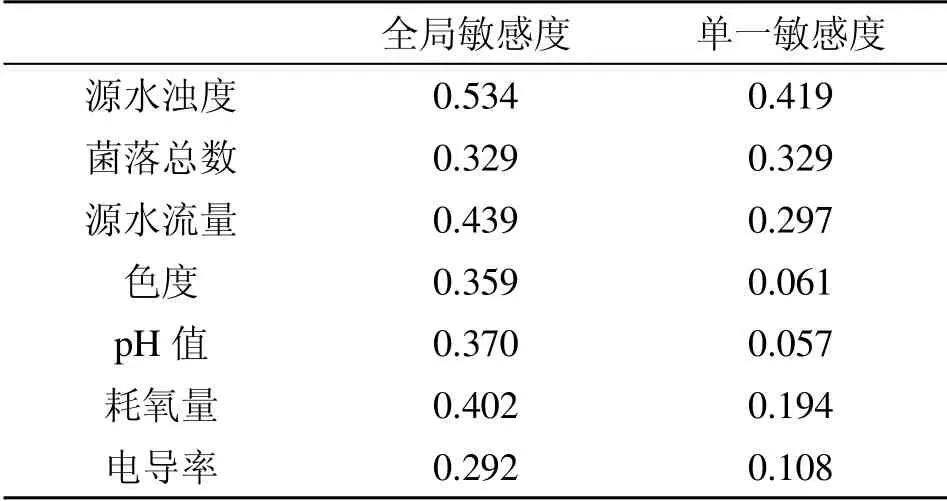
表1 敏感度系数分析计算结果

由敏感度计算结果分析，源水指标影响因素从高至低依次为：源水浊度>源水流量>耗氧量>pH值>色度>菌落总数>电导率，因此投药量应重点围绕流量、浊度、pH值、耗氧量等4个影响因子考虑。依据此结果，本文选取以上4个影响因子指标作为训练样本的维度，投药量作为实际输出值的维度［9-10］，如图2所示。

图2 RBF神经网络模拟水厂投药量结构

2.1.2 样本选取

以昆明市某自来水厂2018年1月—2020年7月共30个月的监测数据作为训练样本，将训练样本矩阵打乱不按照既定年月排列，以此创建4×191的矩阵作为PSO优化RBF神经网络的输入矩阵，X（x1n，x2n，x3n，x4n），n=1，2，…，191。创建1×191的矩阵作为期望拟合的投药量实际值J矩阵。J=J（xn），n=1，2，…，191。随机取自来水厂2018年1月—2020年7月监测数据，创建30个样本量矩阵作为测试矩阵样本。

由于源水指标数量级存在差别，为了防止计算饱和，先对训练样本进行归约处理：

式中，X为水厂数据的训练样本集，Xmax为样本集数据最大值，Xmin为最小值。

2.2 创建函数

PSO算法优化RBF网络训练流程如图3所示。

图3 PSO算法优化RBF神经网络训练流程

2.2 .1使用减法聚类法确定RBF网络隐层节点个数

减法聚类算法可以快速合理地得到数据的聚类中心，根据广义径向基函数特点，可直接将求出的聚类密度最大的训练样本点作为PSO函数的中心点，将样本点数作为RBF网络的隐层节点数。将归约处理后的数据矩阵X（x1n，x2n，x3n，x4n）按照式（6）计算样本i处的密度指标。

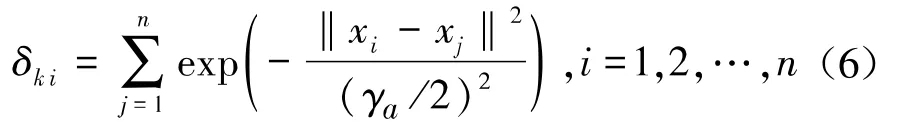
式中，ki为训练样本i处的密度指标，k为迭代更新次数。将首次迭代时密度指标最高的数据点X0=max{x∣ki（x）}作为函数的第一个聚类中心。将第k次更新的密度指标kmax所对应的训练样本点xkmax作为新的聚类中心，采用式（7）修正k+1次样本数据的最大值密度指数。

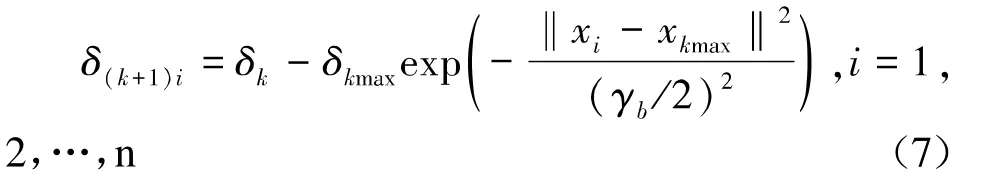
式中，a、b由式（8）确定。依据式（7）计算第k+1次迭代的密度指数k+1判断是否成立，成立则退出，否则重新转到式（7）。计算所得聚类中心数即为广义径向基函数隐层节点个数N。式中为聚类中心点的邻域半径，取值一般为≥0.5时结果较优［11］。

2.2.2 使用公式确定RBF网络高斯基函数标准差

计算高斯函数标准差即扩展函数为：

式中，dmax为聚类中心点之间的最大距离，聚类点存在高维度时，其间距计算采用欧氏距离；N为隐层节点的个数。

2.2.3 使用PSO算法更新RBF网络中心点位置

利用PSO基于群体智能的算法，将减聚类法得到的聚类中心集xk设置为初次迭代的中心点位置，以减少迭代次数，根据式（4）更新粒子每次迭代的运动位置。RBF神经网络是利用误差反向传递调解输出值，本文采用PSO优化训练来使拟合误差缩小。因此，PSO算法的适应度函数f（x）可采用RBF网络均方误差的倒数来进行约束，见式（10）。原始RBF是将训练样本点直接归为某类聚类中心，而PSO优化后的RBF网络归类方式更为敏感、聚类效率高、搜索速度更快。

根据式（1）求得的输出值Y，计算得适应度函数为：

以此约束式（4）以求得每个中心点的位置，中心点Xpo（px1N，x2N，x3N，x4N）为N×10的矩阵。

2.2.4 使用伪逆法计算RBF函数权值

确定中心点个数、位置与标准差之后，下一步是采用伪逆法求取输出权值。假设投药量期望输出矩阵为J=J（xn）；Jij为函数输入向量i的第j个输出值，其中i∈（1，n），j∈（1，n）；kj为函数从隐层节点k到输出节点j的权值，其中k∈（1，N）。则突触权值矩阵可用式（11）求得：

式中，投药量输出矩阵G={gik}，权值矩阵=kj，其中gik是输入向量i的第k个输出值；G+为投药量矩阵G的广义逆，其目标解可由式（12）作奇异值分解求取。

3 函数运行结果

最终生成PSO优化后的RBF神经网络水厂混凝投药模型的函数式，13个隐层数和网络中心点数、最大相对误差12.55%、平均相对误差5.63%、平均绝对误差61.49，迭代次数59次，优化后的函数与原始函数运行结果对比如图4所示。

图4 优化后的函数与原始函数运行结果对比

PSO算法优化后的RBF神经网络相较于水厂机理模型、回归分析、其他神经网络等模型，精度存在明显提高，如表2所示。结果表明，本文提出的PSO优化RBF网络模拟投药量能力优于原始RBF算法，此种模拟可为解决水厂投药量控制提供参考。

表2 优化后的RBF神经网络与其他算法模型运行精度对比

4 结论

1）PSO算法优化后的RBF神经网络在59次便已达到收敛，而原始RBF神经网络在150次左右收敛，可看出PSO算法优化后运算速度更快，能改善RBF网络性能。

2）PSO优化后的RBF神经网络相较于未优化的原始RBF神经网络对于水厂投药量预测平均相对误差降低了25.04%，最大相对误差降低了1.101，可见优化后的RBF相较于原始RBF神经网络模拟精度更高。

3）运用回归方程分析水厂投药量时，常将样本分为高浊与低浊两个方程计算。本文将训练样本矩阵打乱不按照既定月份排列，最后发现高浊度期和低浊度期数据对优化后的神经网络输出影响不大，且预测结果比回归方程求解输出更为精准。

4）机理模型高精度的前提是保证其与水厂的相似性，当更换水厂后，机理模型难以拥有高精度，对于地理位置、工艺流程及源水水质不同的水厂不具有普适性，难以投入生产实践。本文减少了对水厂每个单元的机理模拟，通过PSO优化后RBF神经网络的函数直接得出投药与源水水质的映射关系，获得水厂运行数据库就能借助函数有针对性地进行建模。