基于近似结构风险的ELM隐层节点数优化

黄重庆,徐哲壮,黄宴委,赖大虎

(福州大学电气工程与自动化学院,福州350108)

基于近似结构风险的ELM隐层节点数优化

黄重庆,徐哲壮,黄宴委,赖大虎

(福州大学电气工程与自动化学院,福州350108)

隐层节点数是影响极端学习机(ELM)泛化性能的关键参数,针对传统的ELM隐层节点数确定算法中优化过程复杂、容易过学习或陷入局部最优的问题,提出结构风险最小化-极端学习机(SRM-ELM)算法。通过分析VC维与隐层节点数量之间的关联,对VC信任函数进行近似改进,使其为凹函数,并结合经验风险重构近似的SRM。在此基础上,将粒子群优化的位置值直接作为ELM的隐层节点数,利用粒子群算法最小化结构风险函数获得极端学习机的隐层节点数,作为最优节点数。使用6组UCI数据和胶囊缺陷数据进行仿真验证,结果表明,该算法能获得极端学习机的最优节点数,并具有更好的泛化能力。

极端学习机;结构风险;VC信任;粒子群优化;隐层节点数

1 概述

极端学习机(Extreme Learning Machine,ELM)[1]是一种单隐层前馈神经网络,具有运算速度快、泛化性能好等特点。与普通的前馈神经网络一样,ELM为保证良好的泛化性能,确定合适的隐层节点数量尤为重要。文献[2]指出,ELM虽然避免了梯度下降法存在的问题,但如何确定最优隐层节点数,避免反复试验调节,依然是个亟待解决的问题。文献[3]针对稀疏数据学习问题提出了RCGA-ELM算法,利用遗传算法,优化ELM的隐层节点数、权重w和偏置b,由于涉及多重算子,算法复杂,耗费大量时间。为了降低算法复杂度,提出了S-ELM算法,以5倍交叉验证来选择S-ELM的最佳参数w和b值。PSO-ELM[4], IPSO-ELM[5]和ICGA-SRM-ELM[6]均提出基于粒子群优化(Particle Swarm Optimization,PSO)算法对ELM进行改进,其中,PSO-ELM以均方根误差为优化目标针对ELM中的w和b进行自动选择与优化。IPSO-ELM与ICGA-SRM-ELM类似,强调优化ELM的w和隐层节点数,但IPSO-ELM强调优化ELM的w值,并未涉及隐层节点数的优化问题,而且优化目标函数及迭代选择标准与E-ELM[7]无实质差别。ICGA-SRM-ELM则针对在经验风险最小化原则下对隐层节点数进行分析,但没给出具体形式。文献[8]提出一种能自动确定隐层节点的OP-ELM算法,但是需通过多元稀疏回归和留一(LOO)算法,把开始设定的大隐层节点数删减到最佳值,这与EM-ELM和μGELM[9]一样,需要多重判断标准机制来选择增加或删减节点,使整个算法趋于复杂。此外,μG-ELM用遗传算法优化隐层节点数,给出的优化目标函数仅仅是经验风险最小化,容易出现过学习。这些工作对ELM的可调参数优化研究都做出了或多或少的贡献,但还是存在一些不足之处:(1)没有给出具体的优化目标函数;(2)优化目标函数为经验风险,容易出现过学习或陷入局部最优;(3)利用遗传、差分进化算法优化过程复杂。

本文提出一种SRM-ELM算法,改进VC信任函数以获得凹函数,与经验风险构成近似的结构风险最小化(Structural Risk Minimization,SRM)函数,利用PSO算法寻找SRM最小化时的ELM隐层节点数,为最佳的隐层节点数量。最后,由6组UCI数据和胶囊缺陷数据来仿真验证SRM-ELM的可行性与性能。

2 ELM基本原理

给定N个训练样本(xi,yi),xi=[xi1,xi2,…, xin]T∈Rn,yi=[yi1,yi2,…,yim]T∈Rm,i=1,2,…, N。令隐层节点数量为K,激活函数为g(w,x,b),可构造一个单隐层网络,则ELM模型为:

其中,i=1,2,…,N;j=1,2,…,K;wj=[wj1,wj2,…,wjn]T是连接输入节点到第j个隐层节点的输入权重;βj=[βj1,βj2,…,βjm]T是连接第j个隐层节点到输出节点的输出权重;bj是第 j个隐层节点的阈值。

把N个学习样本分别代入式(1)中可得:

其中:

H称为网络隐层输出矩阵。在一般情况下,隐层节点数远小于训练样本数,即K≪N,H就可能不是一个方阵,因此需求H的伪逆,即Moore-Penrose广义逆。在式(2)中,任意人为给定w和b,以及激活函数g(w,x,b),由Moore-Penrose广义逆定理求得广义逆H+,从而β的解为:

与传统的梯度下降法比较,ELM具有运算速度快和不需反复调整权值等特点[10],但隐层节点数K成为影响ELM泛化性能的重要因素之一,如何自动选择参数K为本文研究重点。

3 SRM-ELM算法

3.1 SRM原理

为克服经验风险最小化存在的过学习问题,文献[11]提出了SRM[11],有如下结论:

对于来自具有有限VC维h的完全有界函数集0≤Q(z,α)≤B,α∈Λ的所有函数,则:

成立的概率至少为1-η。式中R(α)为期望风险;Remp(α)为经验风险,且:

其中,N为样本数量,0＜a≤4,0＜b≤2,η∈(0,1],两类问题中B=1,式(4)右边第2项称为VC信任或VC置信区间。由SRM原则,为使R(α)最小,则必须使Remp(α)和VC信任总和最小。而在给定样本情况下,VC信任取决于整个函数集的VC维h。从文献[12-14]可知,隐层激活函数为sigmoid的神经网络VC维为:

其中,λ为网络的权值个数;l为网络的隐层数;n0为隐层神经元和输出层神经元的总数。

由式(6)可知,h均与λ有关,对ELM来讲,l= 1,则:

其中,n为ELM输入维数;m为ELM输出维数;n和m由样本确定。在n和m已知情况下,由式(7)可知VC维h为隐层节点数K的函数。

根据统计学习理论,令式(4)中B=1,则VC信任可写成:

令a=4,b=1,对h求一次导得:

由式(9)可知,h=N时为仅有的极大值点,即h=N时f(h)取得最大值。

3.2 VC信任函数的改进

利用UCI数据库中的Haberman数据进行VC信任函数式(9)特性分析。图1为VC信任函数f(h)与h的关系。在h∈[0,N]时f(h)为凸函数(经过归一化),则式(4)右边两项的和很难求出全局最小值,相反很容易陷入局部最小值,为此需要对f(h)进行改进。

不难发现,对于任意h,满足下列公式:

则式(4)写成:

另一方面,由式(4)得出概率:

由式(11)和式(12),得:

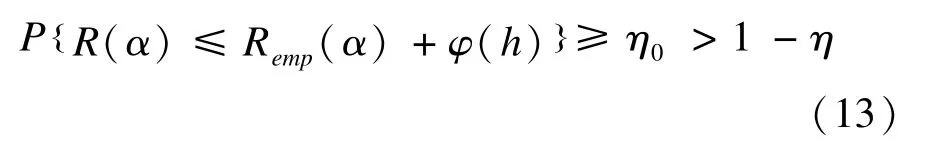
其中,η0∈(0,1],η∈(0,1]。即不等式:

成立的概率至少为1-η。

同样利用UCI数据库中的Haberman数据对改进后的VC信任函数φ(h)与VC维h之间的关系进行分析,如图1所示。从图1可知,改进后VC信任φ(h)为VC维h的凹函数,式(14)是VC维h的函数,可近似获得ELM的泛化能力:

图1 f(h)、φ(h)与h的关系

3.3 PSO基本原理

本文把PSO的位置值直接作为ELM的隐层节点数,PSO每迭代一次相当于ELM训练一次,迭代完毕后即获得最优隐层节点数。

基于惯性权重的粒子速度v和位置p更新公式为:

其中,是粒子i在第k次迭代中的第d维位置;是粒子i在第k次迭代中的第d维速度;为粒子i在第k次迭代中第d维达到的最好位置;为粒子群在第k次迭代中第d维达到的最优位置,d=1,2,…,N;c1,c2为学习因子,一般c1=c2=2;rand1,rand2介于(0,1)之间。

惯性权重τ计算公式为:

其中,τmax和τmin分别表示权重的最大值和最小值;itmax表示最大的迭代次数;NC表示当前迭代的次数。粒子在搜索过程中都有一个最大最小速度和最大最小位置,设置规则见PSO-ELM[4]。

PSO算法的优势在于结构简单,容易实现,且没有过多参数需要调整,可以直接把粒子的位置参数替换成需要优化的决策变量。SRM-ELM直接把PSO的位置值当作隐层节点数,粒子群最终达到的最佳位置就是所要寻找的最优节点数。

3.4 SRM-ELM算法流程

SRM-ELM算法步骤如下:

Step 1 粒子种群初始化。

Step 2 粒子的位置量p直接作为隐层节点数K赋予ELM。

Step 3 在ELM训练的过程中,根据每个粒子的位置值(隐层节点数)计算对应的目标函数R(α,h)。

Step 4 更新粒子最优位置pbest和粒子群最优位置gbest。如果当前粒子的R(α,h)比上一代小,则对应的位置作为目前粒子到达的最优位置;如果当前粒子群的最小R(α,h)比上一代的小,则对应的位置作为目前粒子群到达的最优位置。否则不更新。

Step 5 更新粒子位置p和速度v。根据式(16)和式(17)重新计算粒子的位置和速度。

Step 6 迭代终止。如果NC＞itmax,则优化结束,最后得到的粒子群最优位置即所求的最优隐层节点数K。否则转到Step2循环操作。

PSO和ELM的结合关键在于PSO把位置值赋予ELM,作为隐层节点于ELM主体中,同时把目标函数R(α,h)植入ELM,随着PSO算法的迭代,逐渐接近最好的位置,即逐渐优化出最佳隐层节点数。

4 仿真实验

4.1 参数设置

4.2 UCI数据

本文分别用UCI数据库中的6组2类数据来验证SRM-ELM算法,6组数据如表1所示。

表1 数据信息

在ELM设计时,一般利用交叉验证法在K值预设定的范围内确定最佳隐层节点数K。由Haberman数据进行仿真,假设令K从1～300递增,依次得到对测试样本的分类精度如图2(a)所示,图2(b)为最高测试精度为0.739 6所对应的隐层节点数K=5。从图2可知随着K值继续增加,ELM的测量精度总体上是递减的,当4≤K≤9时,ELM具有很好的测试精度。

利用SRM-ELM算法对6组数据分别连续重复仿真50次,求平均值确定最佳隐层节点数K完成ELM网络设计。图3为Haberman数据的仿真结果,其中图3(a)为50次仿真所得到的隐层节点数K,从50次仿真可知,K值主要集中于6≤K≤9,落在交叉验证法得到K的范围中。图3(b)为第10次仿真中隐层节点数K收敛情况,K从1递增到10,在第16代时收敛于7。对比图3与图2可知,由SRMELM算法所获得K值能够很好地符合由交叉验证法得到的K值。

图2 ELM对Haberman数据的测试精度

图3 隐层节点数K分布

表2 SRM-ELM、ELM与试凑公式N0= +c的性能比较

表2 SRM-ELM、ELM与试凑公式N0= +c的性能比较

数据类型 交叉验证法ELM N0= a+b+c SRM-ELMK测试精度/% K 测试精度/% K 测试精度/% Haberman 4～9 73.62±0.34 3～12 73.45±0.31 6～9 73.57±0.25 Blood 28～45 86.75±0.17 3～12 86.25±0.12 35～40 86.75±0.17 Pima 10～17 79.48±0.12 4～13 79.21±0.03 13～17 79.34±0.03 Ionosphere 35～55 91.58±0.49 7～16 85.64±0.30 27～33 90.59±0.19 Breast Cancer 35～50 99.75±0.15 4～13 99.75±0.15 13～21 99.25±0.10 Australian Credit 13～23 86.58±0.05 5～14 85.00±0.18 14～19 86.58±0.05

4.3 胶囊外观缺陷检测

图4 正常胶囊和各种缺陷胶囊

表3 胶囊缺陷检测结果

5 结束语

本文针对隐层节点数量影响ELM泛化性能的问题,提出一种SRM-ELM算法。SRM-ELM在结构风险最小化原则下,建立隐层节点数与泛化能力的关系函数,利用PSO简单高效的全局搜索能力,优化ELM的隐层节点数,避免了传统方法反复调节实验的繁琐。由6组标准数据实验结果显示,利用SRMELM计算得到的最优隐层节点数均落在交叉验证法得到的ELM最优隐层节点数范围内,保证了良好的泛化性能,与试凑法比较显现出准确性高、推广性好的优势,并且可将该方法用于胶囊外观缺陷检测中。

[1] Huang Guangbin,ZhuQinyu,Siew C K.Extreme Learning Machine:A New Learning Scheme of Feed Forward Neural Networks[C]//Proc.of IEEE International Joint Conference on Neural Networks. [S.l.]:IEEE Press,2004:985-990.

[2] Feng Guorui,Huang Guangbin,Lin Qingping.Error Minimized Extreme Learning Machine with Growth of Hidden Nodes and Incremental Learning[J].IEEE Transactions on NeuralNetworks,2009,20(8): 1352-1357.

[3] Suresh S,Saraswathi S,Sundararajan N.Performance Enhancement of Extreme Learning Machine for Multicategory Sparse Cancer Classification[J].Engineering Applications of Artificial Intelligence,2010,23(7): 1149-1157.

[4] Xu You,Shu Yang.Evolutionary Extreme Learning Machine Based on Particle Swarm Optimization[C]// Advances in Neural Networks.[S.l.]:Springer,2006: 644-652.

[5] Han Fei,YaoHaifen,LingQinghua.AnImproved Extreme Learning Machine Based on Particle Swarm Optimization[C]//Proc.of the 7th International Conference on IntelligentComputing.Zhengzhou, China:[s.n.],2012:699-704.

[6] Saraswathi S,Sundaram S,Sundararajan N.ICGA-PSOELM Approach for Multiclass Cancer Classification Resulting Reduced Gene Sets in Which Genes Encoding Secreted Proteins are Highly Represented Inaccurate[J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics,2010,8(2):452-463.

[7] Zhu Qinyu,Qin A K,Suganthan P N.Evolutionary Extreme Learning Machine[J].Pattern Recognition, 2005,38(10):1759-1763.

[8] Miche Y,Sorjamaa A,Bas P.OP-ELM:Optimally Pruned Extreme Learning Machine[J].IEEE Transactions on Neural Networks,2010,21(1):158-162.

[9] Lahoz D,Lacruz B,Mateo P M.A Biobjective Microgenetic Extreme Learning Machine[C]//Proc.of IEEE Workshop on Hybrid Intelligent Models and Applications.[S.l.]:IEEE Press,2011:68-75.

[10] Huang Guangbin,ZhuQinyu,Siew C K.Extreme Learning Machine[J].Neurocomputing,2006,70(1): 489-501.

[11] Vapnik V N.Statistical Learning Theory[M].New York, USA:Wiley,1998.

[12] Koiran P,Sontag E D.Neural Networks with Quadratic VC Dimension[J].Journal of Computer and System Science,1997,54(1):190-198.

[13] Bartlett P L,Maiorov V,Meir R.Almost Linear VC Dimension Bounds for Piecewise Polynomial Networks [J].Neural Computation,1998,10(8):2159-2173.

[14] Karpinski M,Macintyre A.Polynomial Bounds for VC Dimension of Sigmoidal and General Pfaffian Neural Networks[J].JournalofComputerand System Sciences,1997,54(1):169-176.

[15] 朱启兵,刘 杰,李允公,等.基于结构风险最小化原则的奇异值分解降噪研究[J].振动工程学报,2005, 18(2):204-207.

编辑 顾逸斐

Optimization for Hidden Nodes Number of ELM Based on Approximate Structure Risk

HUANG Chong-qing,XU Zhe-zhuang,HUANG Yan-wei,LAI Da-hu
(College of Electrical Engineering&Automation,Fuzhou University,Fuzhou 350108,China)

The number of hidden nodes is a critical factor for the generalization of Extreme Learning Machine(ELM). There exists complex optimization process,over learning or traps in local optimum in traditional algorithm of calculating the number of hidden layer of ELM.Aiming at the problems,Structural Risk Minimization(SRM)-ELM is proposed. Combining empirical risk with VC confidence,this paper proposes a novel algorithm to automatically obtain the best one to guarantee good generalization.On this basis,the Particle Swarm Optimization(PSO)position value is directly treated as ELM hidden layer nodes,which employs the PSO in the optimizing process with Structural Risk Minimization(SRM) principle.The optimal number of hidden nodes is reasonable correspond to 6 cases.Simulation results show that the algorithm can obtain the extreme learning machine optimal nodes and better generalization ability.

Extreme Learning Machine(ELM);structural risk;VC confidence;Particle Swarm Optimization(PSO); hidden nodes number

1000-3428(2014)09-0215-05

A

TP18

10.3969/j.issn.1000-3428.2014.09.043

教育部博士点新教师基金资助项目(20113514120007);福建省教育厅科技基金资助项目(JA10034)。

黄重庆(1989-),男,硕士研究生,主研方向:图像处理,智能系统;徐哲壮(通讯作者),讲师、博士;黄宴委,副教授、博士;赖大虎,硕士。

2013-08-12

2013-10-10E-mail:297964854@qq.com