主元法在求解竞赛题中的运用
2022-11-28陈志恩
陈志恩
(浙江省永康市教师进修学校附属初中,321300)
对于含有多个变量或含有参数的数学问题,若以题设或习惯中的主要变量解决问题比较困难时,我们可根据题意条件视其他变量为“主元”,或合理使用参数,将参数与变量身份互换,从而降低解题难度,使问题迎刃而解.这一解决问题的方法我们称之为“主元法”.本文以相关数学竞赛试题为例,说明“主元法”在解题中的运用.
一、求解多位数
例1(2003年全国初中数学联赛第二试试题)试求出这样的四位数,它的前两位数字与后两位数字分别组成的二位数之和的平方,恰好等于这个四位数.
解析设前后两个二位数分别为x,y,10≤x,y≤99,则有(x+y)2=100x+y,
∴x2+2(y-50)x+(y2-y)=0.

由于2500-99y必为完全平方数,而完全平方数的末位数字仅可能为0,1,4,5,6,9,故y仅可取25,此时x=30或x=20.
故所求的四位数为2025或3025.
点评本题设出的两个变量x,y地位相同,但为了解题需要,我们视x为“主元”,y为常量,将方程整理成关于x的一元二次方程来求解的.
二、因式分解
例2(第21届“希望杯”全国数学邀请赛初二第二试试题)将代数式x3+(2a+1)x2+(a2+2a-1)x+(a2-1)分解因式,得______.
解析视a为“主元”,得
x3+(2a+1)x2+(a2+2a-1)x+(a2-1)=(x+1)a2+(2x2+2x)a+x3+x2-x-1=(x+1)a2+2x(x+1)a+x2(x+1)-(x+1)=(x+1)(a2+2xa+x2-1)=(x+1)(x+a+1)(x+a-1).
点评在分解含有多个字母的代数式时,视其中一个字母为主元(未知数),将其他字母看成常数,把代数式整理成关于“主元”的降幂(或升幂)排列后,再利用提取公因式、公式法、分组分解法等,或多种方法综合运用进行分解.
三、求代数式的(最)值

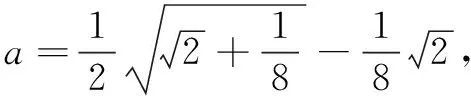
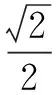
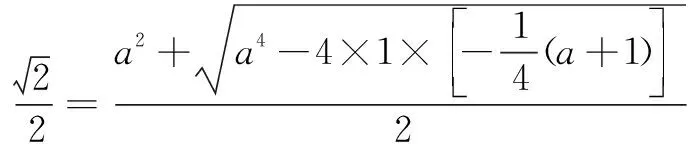
点评该解法巧妙地利用常量与变量的相互转化,并利用一元二次方程的求根公式使问题获解.
例4(2011年全国初中数学竞赛试题)已知x,y,z为实数,且满足x+2y-5z=3,x-2y-z=-5,则x2+y2+z2的最小值是( )
解析对于变量x,y,z,视z为“主元”,这样将另两个变量x,y用z的式子分别表示后,代入目标式求解.

∴x2+y2+z2
=(3z-1)2+(z+2)2+z2
=11z2-2z+5

故选D.
点评本题视z为“主元”,先将x,y均用关于z的式子表示,再代入目标式转化为关于“主元”z的二次函数,最后利用二次函数的性质求解.
四、解方程
例5(第3届“祖冲之杯”初中数学邀请赛)求出所有这样的正整数a,使得二次方程ax2+2(2a-1)x+4(a-3)=0至少有一个整数根.
解析将a视为“主元”,则由ax2+2(2a-1)x+4(a-3)=0,得(x2+4x+4)a=2x+12,∴(x+2)2a=2x+12.
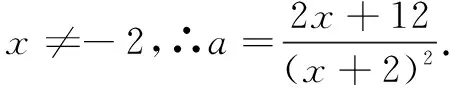
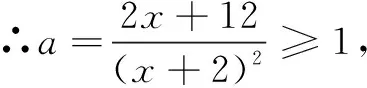
∴2x+12≥(x+2)2,即x2+2x-8≤0,
解得-4≤x≤2,且x≠-2.
又x是整数根,
∴x只能取-4,-3,-1,0,1,2.
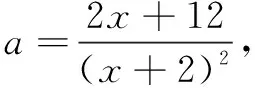
点评本题 “主、次”换位,视正整数a为“主元”,先分离出a,然后根据a是正整数,转化为x的不等式求解.
五、确定取值范围
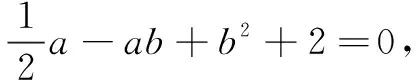
(A)a≤-2
(B)a≥4
(C)a≤-2或a≥4
(D)-2≤a≤4
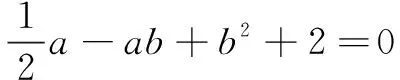
∵b是实数,
即a2-2a-8≥0,
解得a≤-2或a≥4.
故选C.
点评本题视b为“主元”,将已知等式转换为关于“主元”b的一元二次方程,进而利用判别式求解.
例7(第38届“希望杯”全国邀请赛试题改编)当-1≤a≤1时,不等式x2+(a-4)x+4-2a≥0恒成立,则x的取值范围是______.
解析视参数a为“主元”,将原不等式化为(x-2)a+(x2-4x+4)≥0.
令关于a的 “一次”函数y=(x-2)a+(x2-4x+4),
(1)当x=2时,不等式显然恒成立;
(2)当x≠2时,由一次函数图象的性质,得当a=-1时,y≥0,且当a=1时,y≥0,
由此得到关于x的不等式组
对于x2-5x+6≥0,解得x≤2,或x≥3;
对于x2-3x+2≥0,解得x≤1,或x≥2.
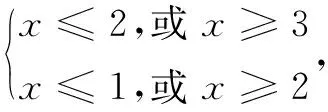
综合(1)、(2),x的取值范围是x≤1,或x=2,或x≥3.
点评在各类考试题中,常出现这样一类问题:系数中含有参数的关于变量x(或x的式子)的一元二次不等式,其参数在某给定的区间上且最高次数为1,求当不等式恒成立时,变量x的取值范围.此类问题如果直接考虑关于x的一元二次不等式则难以处理.但如果视参数为 “主元”,将关于x(或x的式子)的“二次”不等式转化为关于参数的“一次”不等式,再利用一次函数的性质,构建出一个关于变量x的不等式(组),进而求出x的取值范围,则是一条简明而有效的途径.
六、求解函数问题
例8(第22届“希望杯”全国数学邀请赛初三第一试试题)若对于p的任意值,抛物线y=2x2-px+3p+1都过一个定点,则这个定点的坐标是______.
解析因为定点与“参数”p无关,所以可视p为“主元”,将二次函数的解析式化为关于p的一次方程,由各个“系数”均为0求解.
由y=2x2-px+3p+1变形,得
(-x+3)p+(2x2+1-y)=0.
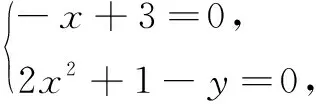
故定点的坐标是(3,19).
点评图象过定点,即与参数无关,我们可视参数为“主元”,将解析式变形整理为含参数和不含参数的两部分,然后令参数的“系数”和不含参数的部分均为0,从而求出定点.
常量与变量不是一成不变的,有时还会相互转化.一个量在一种背景下为变量,而在另一种背景下可以为常量,我们要根据问题的实际情境认清是常量还是变量.只有这样才能理解问题实质,准确有效地解题.“主元法”反映了化归转化数学思想在解题中的应用,是数学思维灵活性的具体表现.在解题中,我们要抓住问题的本质,挣脱“定势”思维框架的束缚,灵活地利用有效的数学方法解决问题.
