挖掘图形特征 优化解题思路

于云霞 王春丽

(山东省荣成市教育教学研究中心,264300) (山东省荣成市实验中学,264300)

一道好的数学题,既能考查学生的基础知识和基本技能,又能提升学生学科的核心素养.在解题教学中,充分挖掘题目内在的数学思想和方法,发挥其应有的功能和价值,必能拓宽学生的解题思路.本文以2019年浙江省富阳市中考模拟试卷第20题为例,谈谈如何引导学生挖掘图形特征,优化解题思路,形成解决几何问题的基本策略.

一、试题呈现

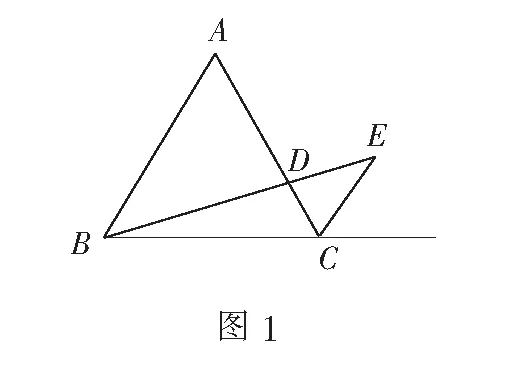
如图1,已知∆ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长,与CE交于点E.

(1)求证:∆ABD∽∆CED;

(2)若AB=6,AD=2CD,求BE的长.

二、试题分析

此题不仅考查了学生对等边三角形的性质、相似三角形的判定与性质、锐角三角函数等知识点的掌握情况,还考查了学生对转化、数形结合、几何直观等数学思想方法的运用能力.

本题第(1)小问比较简单,略.下面只对第(2)问进行解法探究.

三、解法展示

1.利用锐角三角函数解斜三角形

解法1如图2,过点E作EM⊥BF,垂足为M.

∵∆ABD∽∆CED,AD=2CD,

∵AB=6,∴CE=3.

在Rt∆CEM中,∠ECM=60°,

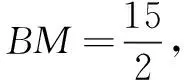
解法2如图3,过点B作BM垂直于EC交EC的延长线于点M.

在Rt∆BCM中,∠BCM=60°,BC=6,

在Rt∆BME中,

∵EM=CM+CE=3+3=6,

说明在斜∆BCE中,已知两边及两边的夹角,通常作垂线,将斜三角形的问题转化为直角三角形问题来解决.

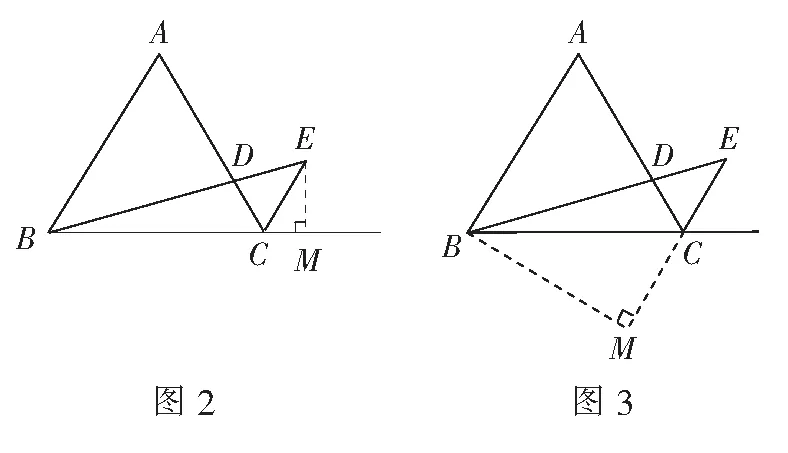
解法3如图4,过点B作BM⊥AC,垂足为M.

在Rt∆ABM中,∠A=60°,AB=6,

∵AD=2CD=4,∴DM=1,

∵∆ABD∽∆CED,

解法4如图5,过点E作EM⊥CD,垂足为M.

∵∠ECM=60°,CE=3,

∵∆ABD∽∆CED,

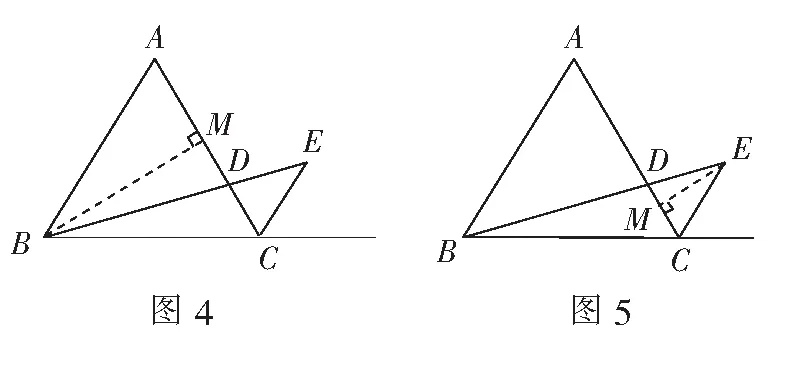
解法5如图6,过点D作DM垂直BC,垂足为M.∵∠DCB=60°,DC=2,

∵BC=6,∴BM=BC-CM=5,

∵∆ABD∽∆CED,

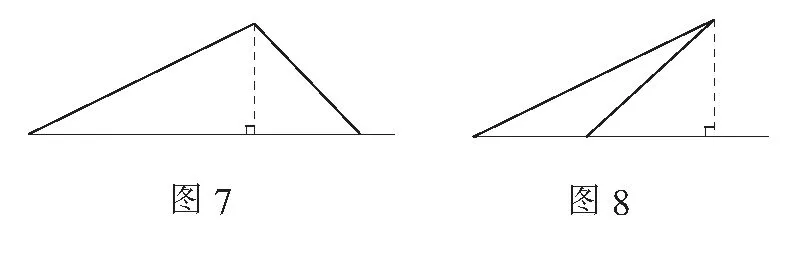
说明在几何解题教学中,通过作三角形的内高或者外高,如图7“背靠式”、图8“叠合式”将斜三角形转化为直角三角形来解决问题,体现了化“斜”为“直”的数学思想.

2.构建“手拉手”模型

解法6如图9,取CG=CE,连结AG,过点A作AM⊥BC,垂足为M,则由AC=BC,∠ACG=∠BCE=120°,可得∆ACG≌∆BCE,∴AG=BE.

∵BC=AB=6，

在Rt∆AMG中,MG=CM+CG=6,

说明如果题目中出现共顶点、等线段条件,我们可以选择构建“手拉手”模型来解决问题.

四、解后反思

1.认识基本图形,回归本源思考

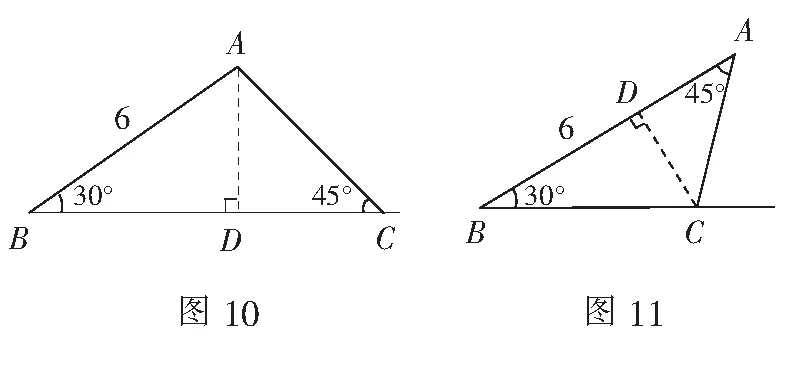
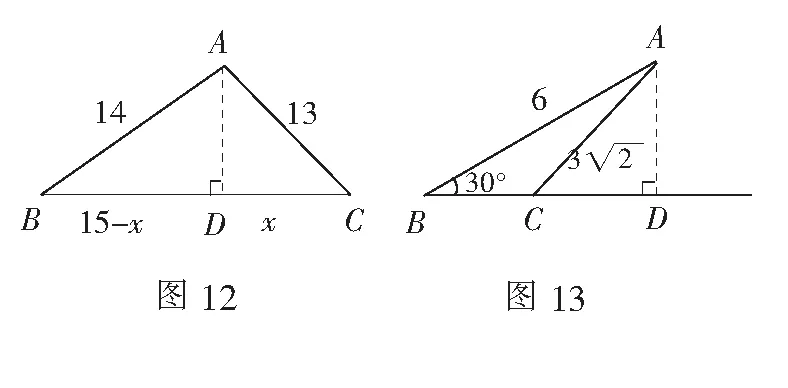
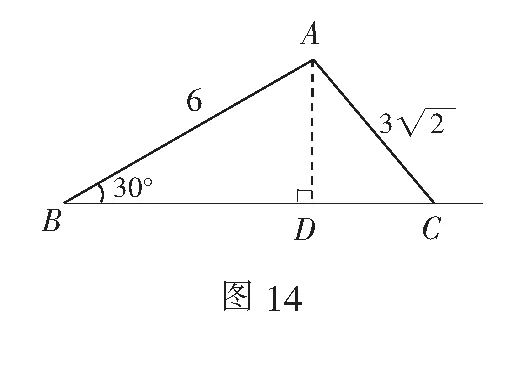
在几何题目中,经常会出现结构简单内涵却很丰富的基本图形,这些图形往往会蕴含一些静态的数量关系，因此，认识并理解这些基本模型,有利于提升学生的高阶思维能力.此题在解斜三角形的时候,由已知条件可以得到斜三角形的两边及其夹角(用“SAS”表示),可将探究三角形全等的方法进行有效迁移,来解决有这样特点的斜三角形.在教学中,教师可以引领学生对知识进行拓展,若斜三角形中已知元素为“AAS”如图10,“ASA”如图11,“SSS”如图12,“SSA”如图13和图14,即斜三角形满足已知两角一边或者两边一角,或者三边的条件,也是可解的.

2.优化解题思路,把握通法通则

在解题过程中,如果我们能够对问题进行多角度的思考,优化解题思路,就能够激发学生思维的灵活性,形成解决问题的通性通法.在具体解题过程中我们会发现,许多题目中的基本模型都会缺失部分元素,需要学生添加辅助线将其补全,这时就需要学生具有几何直观能力和空间想象能力,从不同的切入点联想几何模型,产生丰富多彩的构图方案,继而得到不同的解题思路.例如，此题要求的是线段BE的长度问题,已知条件中有等边三角形,可以建立学生最熟悉的手拉手模型,通过转化的思想,将边BE转化为直角三角形的斜边长,借助勾股定理解决问题.另外,函数思想是贯穿于代数和几何两大领域的重要数学思想,在解决线段长度的问题时,数形结合不失为一种解决问题的基本方法.

总之,解题过程中,我们只有实现“怎样做”到“怎样想”的转变,弄清思想方法的来源,挖掘基本图形特征,把握通法通则,才能够在解题的过程中以不变应万变,真正将数学核心素养落到实处.