剖析结构 启迪思维 聚焦素养——一道填空压轴题的解法探究

陈玉松

(安徽省濉溪县城关中心学校,235100)

在解题教学中,教师应适时地引导学生从不同的角度,用不同的思维方式去观察、联想、分析,并根据问题的特定条件探索出多彩解题思路,使学生的思维触角伸向不同的方向、不同的层次.这样不仅能巩固所学知识,还可以开拓学生的思路,较好地提升学生的数学思维和核心素养.本文以一道九年级月考填空题为例,着力从不同视角挖掘基本图形,探寻解法的自然生成过程.

一、试题呈现

如图1,在等腰Rt∆ABC中,∠ACB=90°，AC=15,点E在边BC上,CE=2EB,点D在边AB上,CD⊥AE,垂足为F,则AD的长为______.

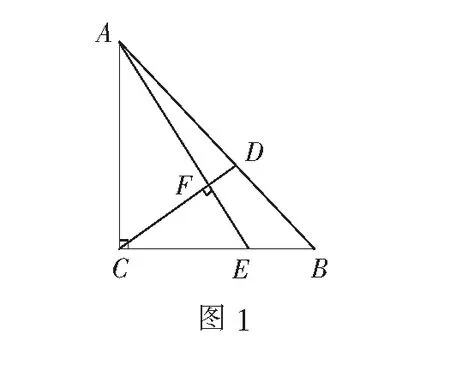
二、试题简析

本题以等腰直角三角形为背景,主要考查三角形相似的判定与性质、全等三角形的判定与性质、勾股定理、平行线分线段成比例定理以及三角函数等数学核心知识.本题条件简洁,构图新颖,内涵丰富,借助图形可从多角度去思考问题.从数学能力上看,要想正确解答此题,需要学生具备分析问题和解决问题的能力.若能引导学生抓住图形的特征条件构建基本图形,解题自然水到渠成.

三、解法探究

视角1利用“A”型平行相似

解法1∵∠ACB=90°,CD⊥AE，

∴∆ACE∽∆CFE∽∆AFC,

∵AC=BC,CE=2BE,

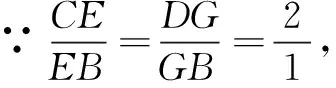
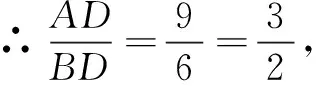
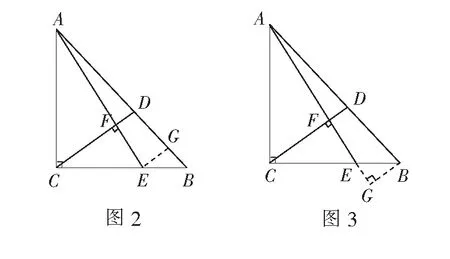
解法2如图3,过点B作BG⊥AE交AE延长线于点G.

∵CD⊥AE,∴CD∥BG,

视角2利用“X”型平行相似

解法3如图4,过点E作EG∥AB交CD于点G.

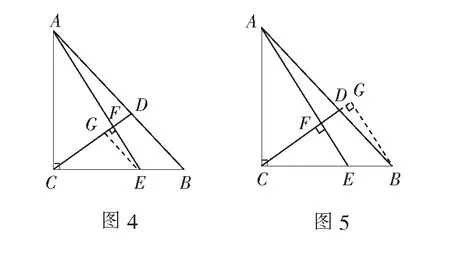
评注以上四种解法都通过添加平行线或垂线,构造平行相似，再结合相似三角形的性质将线段进行转化,求得AD和BD之间的数量关系,从而解决问题.

视角3运用勾股定理及相似三角形

解法5∵AC=BC=15,CE=2BE,

在Rt∆ACE中,由勾股定理,得

由解法1,可知AC2=AF·AE,

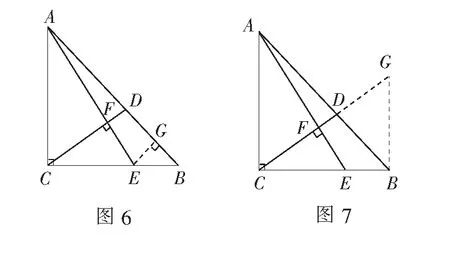
如图6,过点E作EG⊥AB于点G,则得等腰Rt∆BEG,

评注勾股定理是平面几何中应用最为广泛的定理.而本题中的所有线段的长都是确定的,故可利用勾股定理可求出相应线段长,再结合相似三角形即可顺利求解.

视角4巧用全等三角形

解法6如图7,过点B作BG⊥BC交CD延长线于点G.

∵CD⊥AE,∴∠CAE=∠BCG.

又AC=CB,∠ACB=∠CBG,

∴∆ACE≌∆CBG,∴CE=BG=10.

解法7如图8,过点B作BG∥CD交AC延长线于点G.

∵CD⊥AE,

∴∠CAE=∠BCD=∠CBG.

∵AC=CB,∠ACB=∠BCG.

∴∆ACE≌∆BCG,∴CE=CG=10.

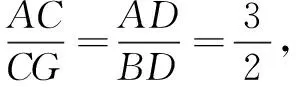
评注这两种解法都是通过添加平行线构造全等三角形,将线段CE进行转化,再运用平行线分线段成比例定理,巧妙地得出了线段AD和BD的比例关系,进而问题得以破解.

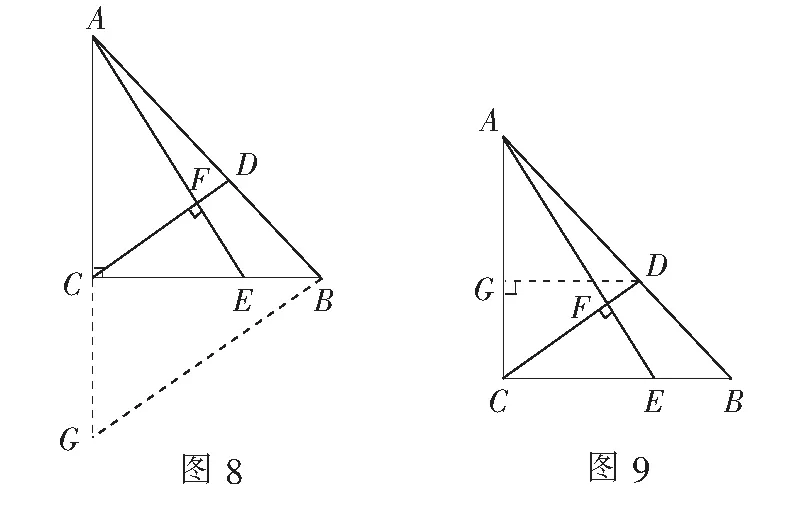
视角5借助三角函数

解法8如图9,过点D作DG⊥AC于点G，则∠DCB=∠GDC.

∵CD⊥AE,∴∠CAE=∠DCB,

设CG=2x,则DG=AG=3x.

∵AC=15,∴2x+3x=15,解得x=3.

评注通过作垂线段,将∆ACD分割成两个特殊的直角三角形,通过设出未知数表示出相关线段的长,进一步构建方程,问题便迎刃而解.

四、解题反思

1.洞察图形结构,打开思维视角

波利亚说:“学习数学的主要目的在于解题.”解题是一种本领,是一个不断联想,自然生长,逐步反思的过程,我们只有在模仿、实践、总结过程中才能感悟它的真谛.在本题中,学生可根据图形剖析结构,抓住特殊角、相等边、三等分点、垂直等特征条件,并对其进行加工和再创造,进一步打开思维,多角度地思考问题,从而得到不同的解法.因此在日常的教学中,教师应重视基本图形的辨识,培养学生的识图能力,引导学生从特征条件出发,寻找基本图形,尝试构建图形,从而实现思维突破.

2.感悟一题多解,发展核心素养

一题多解有助于学生思维的多向发展,是完善思维品质的有效途径.在解题教学中,教师可选择典型习题,引导学生根据题目的条件、结论与图形,挖掘隐性条件,再进行重新配置与组合使学生获得多种解题方法.如本题中,为了求出AD的长,用到了“全等三角形”“相似三角形”等数学模型,这就需要具有一定的数学建模素养;在借助三角函数解决问题时,大大简化了计算过程,这就需要具有较高的几何直观素养.因此教师要融合各阶段知识,引领学生深度思考,建立和完善数学知识结构体系,优化学生的思维品质,发展数学核心素养.