几何极值

单 墫

(南京师范大学数学科学学院,210023)

如图1，过∠A内一定点P引直线与∠A的两边交于点B，C.

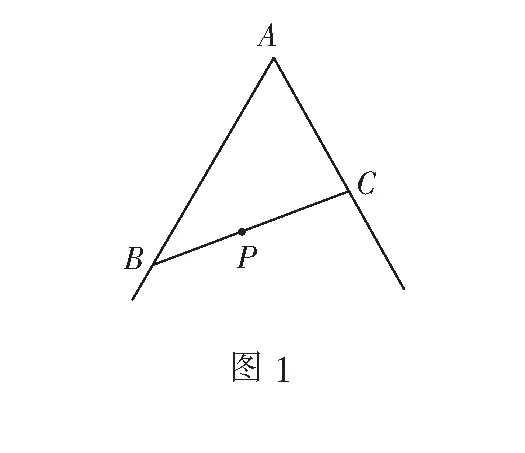
(1)当PB=PC时，∆ABC面积最小;

(2)当BC边外的旁切圆与BC切于点P时，∆ABC周长最小；

(3)当AB=AC时，PB·PC最小.

刘国梁老师选了一批几何极值问题，颇有趣.笔者做了与中学几何有关的几题，其中初中部分即以上3题.

证明(1)如图2，对任一过点P的线取B′C′(点B′，C′分别在AB，AC的延长线上)，则有∠BCC′>∠B，所以过点C在∠BCC′内作CD，使∠BCD=∠B(即CD∥AB).

设CD交PC′于点D，则由BP=PC，可得

∆PBB′≌∆PCD.

所以S∆AB′C′>S∆ABC.

(2)如图3，设旁切圆分别切直线AB，AC于点E，F，则BP=BE，PC=CF，所以∆ABC的周长等于AE+AF.

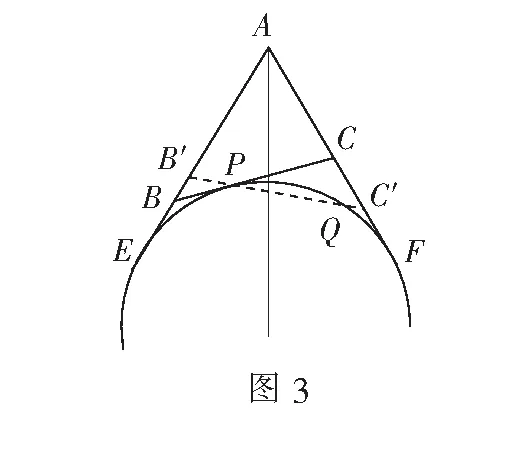
对另一∆AB′C′(B′C′过点P且点B′,C′分别在AB，AC的延长线上)，设B′C′交旁切圆于另一点Q.

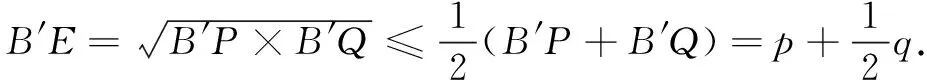
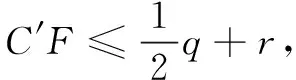
所以B′E+C′F≤p+q+r.

所以∆AB′C′周长=AB′+AC′+B′C′≥AB′+B′E+AC′+C′F=AE+AF=∆ABC周长.

(3)如图4，∠B=∠ACB>∠C′.

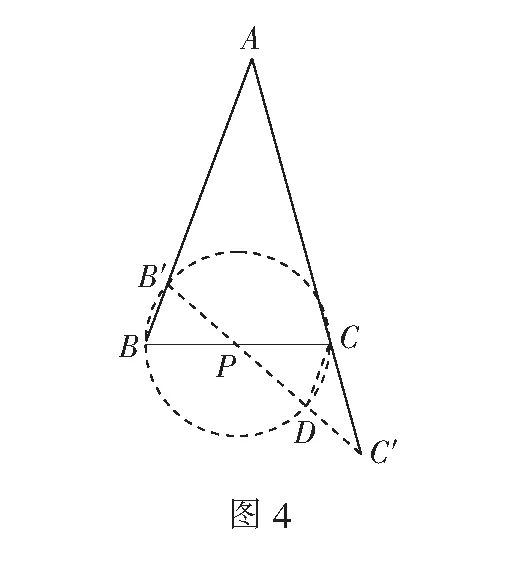
设⊙B′BC交B′C′于点D，则∠B′DC=∠B>∠C′，所以点D在线段PC′上.

所以PB·PC=B′P·PD