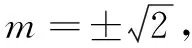依托不动点新定义 探究函数值不变性

李发勇

(四川省巴中市巴州区大和初中,636031)

对于函数g(x),如果存在x0,使得g(x0)=x0,则x0叫做函数g的不动点.本质上,不动点问题就是方程的根的求解问题.其思考方法:依据定义,不动点问题转化为方程g(x)=x的根或函数g(x)=x与直线y=x的交点的横坐标问题.本文举例说明与不动点有关的问题,供分享.

一、不动点的存在性

(2)函数y=3kx+s-1(k,s是常数)的图象上存在“梦之点”吗?若存在,请求出“梦之点”的坐标;若不存在,说明理由.

(2) 由y=x,得(1-3k)x=s-1.

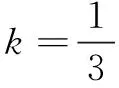
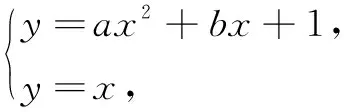
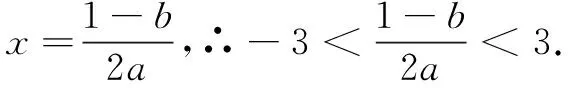
由|x1-x2|=2,得(b-1)2=4a2+4a,

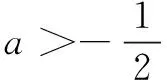
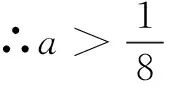
例2(2013届景德镇市九年级第三次质检题)新定义:若t=at2+bt+c成立,则称点(t,t)为抛物线y=ax2+bx+c(a≠0)上的不动点.设抛物线C的解析式为y=ax2+(b+1)x+(b-1)(a≠0).

(2)对于任意实数b,实数a应在什么范围内,才能使抛物线C上总有两个不同的不动点?

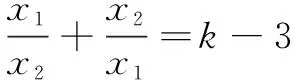
解(1)由题意,得

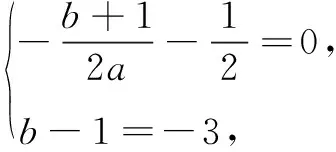
∴抛物线C的解析式为y=x2-x-3.

令x=x2-x-3,

解得x1=-1,x2=3.

∴不动点为(-1,-1)和(3,3).

(2)若抛物线C有两个不同的不动点,则由x=ax2+(b+1)x+(b-1),整理得ax2+bx+(b-1)=0.

∴Δ=b2-4a(b-1)>0,

即b2-4ab+4a>0.

∵b为任意实数,且使得上式成立,

∴(-4a)2-4×1×4a<0,

整理，得a2-a<0,

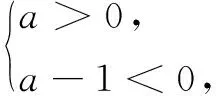
解得0

∴实数a的范围是0

(3)k=-1或k=-2.(过程略)

二、不动点的应用

例3(2003年绵阳中考题)若点P(t,t)在抛物线上,则点P叫做抛物线的不动点.设抛物线y=ax2+x+2经过点(-1,0).

(1)求这条抛物线的顶点和不动点的坐标;

(2)将这条抛物线进行平移,使其只有一个不动点.证明平移后的抛物线的顶点在直线4x-4y-1=0上.

分析(1)设出不动点的坐标,并代入抛物线解析式中,即可求出不动点的坐标.

(2)先设出平移后抛物线的解析式,再由这个抛物线只有一个不动点可得出平移后抛物线的顶点坐标所满足的关系式.

解(1)由抛物线y=ax2+x+2经过点(-1,0),可得a-1+2=0,∴a=-1,

(2)设平移后的抛物线为y=-(x-a)2+b,则由抛物线只有一个不动点,可得方程x=-(x-a)2+b,即x2-(2a-1)x+(a2-b)=0只有一个解,

∴Δ=(2a-1)2-4(a2-b)=0,

即4a-4b-1=0.

故平移后抛物线的顶点在直线4x-4y-1=0上.

例4(2019年上海中考题)如图1,在平面直角坐标系xOy中,已知抛物线y=x2-2x,其顶点为A.

(1)写出这条抛物线的开口方向、顶点A的坐标,并说明它的变化情况;

(2)我们把一条抛物线上横坐标与纵坐标相等的点叫做这条抛物线的“不动点”.

① 试求抛物线y=x2-2x的“不动点”坐标;

② 平移抛物线y=x2-2x,使所得新抛物线的顶点B是该抛物线的“不动点”,其对称轴与x轴交于点C,且四边形OABC为梯形,求新抛物线表达式.

解(1)抛物线y=x2-2x的开口向上,顶点A的坐标是(1,-1).

抛物线的变化情况:抛物线在对称轴左侧的部分是下降的,右侧的部分是上升的.

(2)① 设抛物线y=x2-2x的“不动点”坐标为(t,t),则t=t2-2t,解得t1=0,t2=3.

∴抛物线y=x2-2x的“不动点”的坐标是(0,0),(3,3).

② 设新抛物线的顶点B(m,m)是其“不动点”,则新抛物线的对称轴x=m与x轴的交点为C(m,0).

∵四边形OABC是梯形,

∴对称轴x=m在y轴左侧.

∵BC与OA不平行,∴OC∥AB.

又点A的坐标为(1,-1),点B的坐标为(m,m),∴m=-1,即新抛物线是由抛物线y=x2-2x向左平移2个单位得到的.

故新抛物线的表达式是y=(x+1)2-1.

新定义试题属于创新类试题,主要考查学生对“新定义”的理解和认识,以及灵活运用知识的能力.对于新定义型问题,我们需要将“新定义”与已学知识联系起来,利用已有的知识经验来解决.