基于多目标约束的下降段航迹预测方法研究
2022-11-22樊智勇张泽栋杜航航
樊智勇, 张泽栋, 杜航航
(中国民航大学,天津 300000)
0 引言
随着航电技术的发展,四维航迹运行已成为未来航空运行的目标[1]。精确、多方位地预测航空器下降段飞行轨迹,能够极大地降低航空器未来下降飞行的不确定性,提高空中交通的可预测性[2]。
针对下降段航迹预测的方法主要分为以下3种。
其一,将航迹预测视作随机线性混杂系统的单、多模型状态估计问题。以航空器运动方程构建状态转移矩阵以实现对飞行过程中位置、速度等状态的估计。单模态估计模型包含卡尔曼滤波(Kalman Filter,KF)算法、粒子滤波算法以及隐马尔可夫模型(HMM)及其各类扩展改进算法[3-4]。多模态估计模型包括广义伪贝叶斯算法、交互多模型(Interacting Multiple Model,IMM)算法等[5-6]。
其二,通过机器学习模型训练航空器轨迹预测。以历史飞行信息作为输入特征预测未来飞行轨迹。针对航迹预测问题的典型机器学习模型包含长短期神经网络(Long Short-Term Memory,LSTM)和深度神经网络(Deep Neural Networks,DNN)等[7-8]。此外,机器学习模型还包括遗传算法(Genetic Algorithm,GA),蚁群算法以及支持向量机(Support Vector Machine,SVM)等[9]。
其三,构建航空器运动学模型预测飞行航迹。通过分析航空器受力与三维运动、飞行意图的关系,建立动力学方程,预测未来连续时间点的航空器运动轨迹。在此研究领域通常采用点质量模型(Point-Mass Model,PMM)理念为满足相应需求进行快速仿真环境下的运动建模[10-11]。
综上所述,针对航路限制、性能限制及成本指数约束下的航路预测问题,结合动力学领域应用,提出一种多目标约束下的航空器下降段航迹预测方法。将多目标约束问题代入反向积分航迹预测中,以下降顶点(End of Descent,E/D)为反向迭代起始点,将各航路信息、航空器性能限制为约束点,动态调整成本指数,预测生成对应的飞行轨迹,确保满足航路限制需求及提高燃油经济效益。
1 航迹预测方法流程
基于PMM理论并参考航空器性能数据、特征参数及飞行环境,通过Visual C++构建多领域基础数学模型。结合基础数学模型、航路点限制、航空器性能限制以及成本指数,构建航空器下降段航迹预测模型,如图1所示。

图1 下降段航迹预测流程Fig.1 Prediction process of descent-stage trajectory
1) 在下降段反向积分预测过程中,为解决迭代起始点E/D点状态信息未知的问题,通过航空器巡航阶段状态数据来估计下降终点E/D的航空器全重。
2) 以E/D点航空器全重为反向积分起点,以时间或高度作为积分步长。
第一阶段为进近程序构成的几何下降航径。以航路点坐标及高度、速度限制确定各航段的固定航迹角(Flight Path Angle,FPA)及目标空速,逆向迭代各时间点的航空器状态数据。
第二阶段为慢车下降航径。以成本指数确定经济指示空速及经济马赫数,再结合航路点限速以及性能限制来重复修正目标空速,最终确定慢车下降阶段中各航段目标空速、目标高度等。同时,需考虑相邻航段的目标空速不同所导致的速度变化问题,从而计算出逆向的航空器慢车下降航迹。
3) 积分过程在高度迭加到巡航高度时终止,得到下降起点(Top of Decent,T/D)坐标。为减少最初估算E/D点全重所带来的误差,将从E/D点反向积分迭加到T/D点后的燃油消耗量校正迭代起始点E/D的航空器全重,再次预测生成航空器下降航迹,直至燃油消耗量收敛到一点。
4) 生成航路信息、成本指数及航空器性能约束下的下降航迹及对应时间点的多维状态数据,包含距离E/D点水平路程、高度、空速、升降率、N1目标值、推力、燃油流量及燃油消耗量。
2 航迹预测模型
为估算E/D点航空器全重,首先建立航空器及飞行环境的基础数学模型。下文中未特别说明变量均为标量。
2.1 基础数学模型
2.1.1 大气模型
外界大气温度TOAT为
(1)
式中:T0为标准大气温度;h为起始高度;ΔTISA代表降落目的机场的外界大气温度与T0的差值。
外界大气压强P为
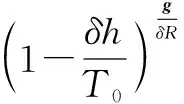
(2)
式中:计算推力、阻力时为使单位统一,压强单位采用英寸汞柱,标准大气压强P0=29.921 26 inHg(1 inHg=254 Pa);δ/T0为温度修正,δ为一常系数;R为通用气体常数;g为重力加速度。
航空器所在的高度大气密度ρ为
(3)
式中,ρ0为标准大气密度,由于推力、阻力计算时单位为磅,故ρ0单位为slug/ft3(1 slug≈14.593 9 kg,1 ft≈304.8 mm)。
2.1.2 气动模型
航空器飞行过程中阻力算式为
(4)
式中:阻力系数CD与寄生阻力CD0、Oswald系数COswald、升力系数CL以及展弦比RAspect有关;VTAS为真空速。
发动机推力模型为
(5)
式中:Tstatic为单发动机基础推力值;CThrust为修正推力系数;P0/P为气压比倒数;Dram为单发动机冲压阻力值。其中,CThrust通过航空器性能特征曲线插值得到的基础推力系数经由当前外界温度、当前马赫数、N1目标值修正获得。
燃油流量fFF模型为
(6)
式中,VTSFC为单位推力耗油率(Thrust Specific Fuel Consumption,TSFC)。
2.1.3 速度转换模型
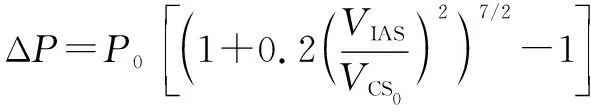
(7)
式中:ΔP为全压与静压的压差(Differential Pressure);VCS为所在高度对应声速。
2.1.4 动力学模型
基于PMM理论,在航迹坐标中得到航空器下降段的动力学方程。无侧滑时航空器动力学方程描述为
(8)
式中:m为质量;G为航空器所受重力;T′为推力;α为迎角;φp为发动机安装角;γ为航迹角。
从能量角度及式(8)分析得[12]
(9)
2.2 初始点航空器全重估算
以E/D点作为反向积分起始点来预测航空器下降轨迹,由于起始下降位置未知,需估算出航空器在E/D点的全重WE/D。
为估算E/D点航空器全重WE/D,设固定航迹角为aFPA、固定下降率为VVS(通常取-1500~-2000 ft/min[13]),则根据几何关系可求得粗略的T/D点位置,并计算航空器巡航状态下到此T/D点的航空器全重WT/D。
再从T/D点以慢车推力下积分至E/D点,通过航空器在不同时间点的高度、马赫数及N1目标值修正式(5)中推力系数CThrust,结合式(6)估算下降阶段的燃油消耗WF,最终得
(10)
此处WE/D为粗略估计,后文会校正。
2.3 进近航段预测模型
进近航段由各受限制下降航路点组成,估算出E/D点航空器全重WE/D后,以WE/D及高度hE/D作为反向积分起始点输入,将dh作为积分步长,通过各航路点限制确定几何航段的固定aFPA,如图2所示。

图2 几何下降航段Fig.2 Geometric descent stage
对于进近程序中的下降航段,N1目标值不等于慢车推力下的N1值,无法通过N1值确定航空器推力。所以,从能量角度分析,以航段首、尾航路点限制速度确定目标空速,并结合几何路径的三角函数关系及式(9)计算推力,过程如下。
首先,假设从航路点a到相邻下一航路点b,已知两航路点限高为ha,hb,航路点限速为Va,Vb,设dh为积分步长,则航迹角
(11)
将指示空速变化率按积分步长均匀分配给各积分步长区间后,对应指示空速变化
(12)
则在此积分区间内的平均真空速VTAS可以通过式(7)转换得到,再根据几何关系计算出平均升降率VVS以及dt。参考飞机气动参数,将VTAS代入式(4)计算当前状态所受阻力D′。
然后,将式(9)等式变换,求得此积分区间对应发动机平均推力为
(13)
将T′代入发动机性能特性曲线插值求得当前N1目标值。再将T′代入式(6)计算此区间的燃油消耗量以及航空器全重,即
(14)
同时,此位置距离E/D点的水平路程为
xtoE/D=xtoE/D+dx=xtoE/D+VTAScosaFPA。
(15)
最终,生成此积分步长后的多维航空器状态数据。
以上述过程类推,以E/D点作为航路点a,下一航路点为b,当h迭加到h≥hb时,计算流程转入下一航段,直至高度迭加到进场阶段初始航路点高度,衔接至慢车下降航段预测。输出进近下降航段中各时间点对应的多维状态数据为Xt=(ht,xtoE/Dt,VIASt,VTASt,Mat,VVSt,T′t,fFFt,WFt,N1)。
2.4 慢车航段预测模型
以进近航段迭代后输出的航空器全重W、慢车下降航段的起始高度h及成本指数或航路点限速所确定的目标空速VIAS作为慢车航段的输入。
成本指数及航路限制确定目标空速。为解决航空器慢车下降阶段中目标空速选取问题,令目标空速VIAS等于航路点限速或经济指示空速的最小值,并判断该空速是否满足性能限制。若反向积分过程中某时间点不满足上述约束,校正该航段目标空速并重新反向积分。其中,经济指示空速由成本指数决定,成本指数定义为时间成本Ct和燃油成本CF之比。
如图3所示,查询发动机的飞行管理计算机数据库文件可知,根据航空器在下降顶点的全重以及成本指数插值确定经济指示空速,通过调整成本指数得到对应目标经济指示空速。

图3 飞机经济指示空速与成本指数关系Fig.3 Relationship between IAS and CI
减速航段时,针对相邻航段的目标空速变化导致前后航段空速不一的情况,以时间dt为积分步长、以匀减速dVIAS计算推力
(16)
式中,dVTAS由式(7)转换得到,阻力D由航空器升力系数与阻力系数关系代入式(4)得到。
其他多维信息的计算方式与进近下降阶段相同,已知推力T′及升降率VVS后可分别求得,从而得到航空器慢车下降中减速段的预测航迹及多维状态数据Xt。
非减速下降航段时,针对慢车航段中非减速航段,设dh为积分步长,N1目标值为空中慢车推力N1IDLE,则将经济下降指示空速或航路点限速确定的目标空速VIAS代入式(7)求出VTAS和Ma。慢车非减速下降阶段推力T′对运动状态影响甚微,由N1目标值N1IDLE代入式(5)求出。
通过式(9)等式转换后计算平均升降率为

(17)
为求距离E/D点水平路程xtoE/D,需求出此航空器在此积分区间所对应的航迹角aFPA,即
aFPA=arcsin(VVS/VTAS)。
(18)
将aFPA代入式(15)得对应xtoE/D。最终得到航空器在慢车航段中非减速航段的各时间点对应的多维状态数据Xt。
以上述过程反向积分并迭代高度h,当h大于等于巡航高度hCRZ时计算终止。
2.5 误差校正
h大于等于hCRZ时,迭代终止,得到T/D点位置及对应航空器预测航迹。为减少初始估算E/D点航空器全重WE/D造成的误差,返回迭代后得到的航空器整个下降航段的燃油消耗量到E/D点,校正E/D点的航空器全重。
已知经由迭代后得到的T/D点位置信息,计算航空器从巡航阶段到达T/D点位置后的剩余全重为
WT/D=WT/C-WFCRZ
(19)
式中:WT/C为航空器在爬升顶点T/D的全重;WFCRZ为巡航阶段燃油消耗。
已知迭代终止时的整个下降航迹燃油消耗WF,校正初始估算的E/D点航空器全重为
WE/D=WT/D-WF
。
(20)
由此,航空器全重WE/D作为航迹预测模型输入并重新迭代计算,直至WF收敛至一点。最后,导出校正后的下降预测航迹以及各时间点对应航空器状态数据Xt。
3 仿真验证
将下降航段航路信息、降落机场空域限制信息、多电飞机的性能数据、气动数据及特征参数等导入仿真程序。对比真实航迹QAR数据,验证是否可动态调节成本指数后输出对应成本效益的飞行下降曲线及其多维状态数据,是否满足航路限制及燃油经济性的要求。
3.1 数据输入
在预测模型中导入某多电飞机发动机模型、气动模型等所需性能数据库参数,参考真实航迹航路点信息,添加导航数据库。截取如图4所示巡航、慢车以及进近航段水平航路点信息,包含各航路点位置及限速限高信息,并将此信息及航空器性能数据导入仿真程序中。图4中限高10/50表示10 m/50 ft,限速160表示160 kn(1 kn≈1.852 km/h)。
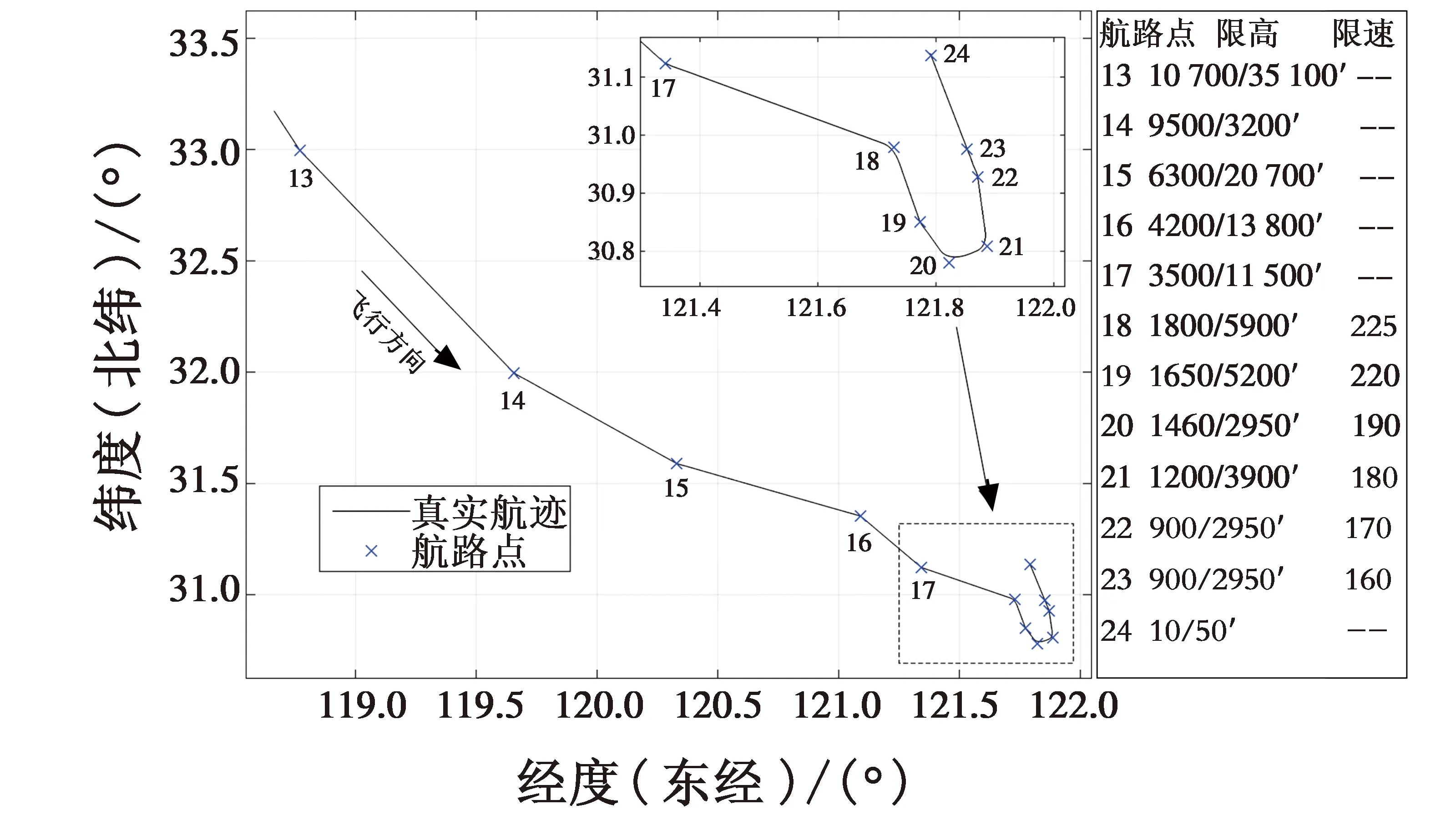
图4 水平航路信息Fig.4 Horizontal route information
3.2 验证并分析
为直观对比在成本指数以及航路限制约束下的预测航迹,动态调整成本指数,将仿真程序输出数据转换为如图5所示的二维垂直剖面预测曲线。
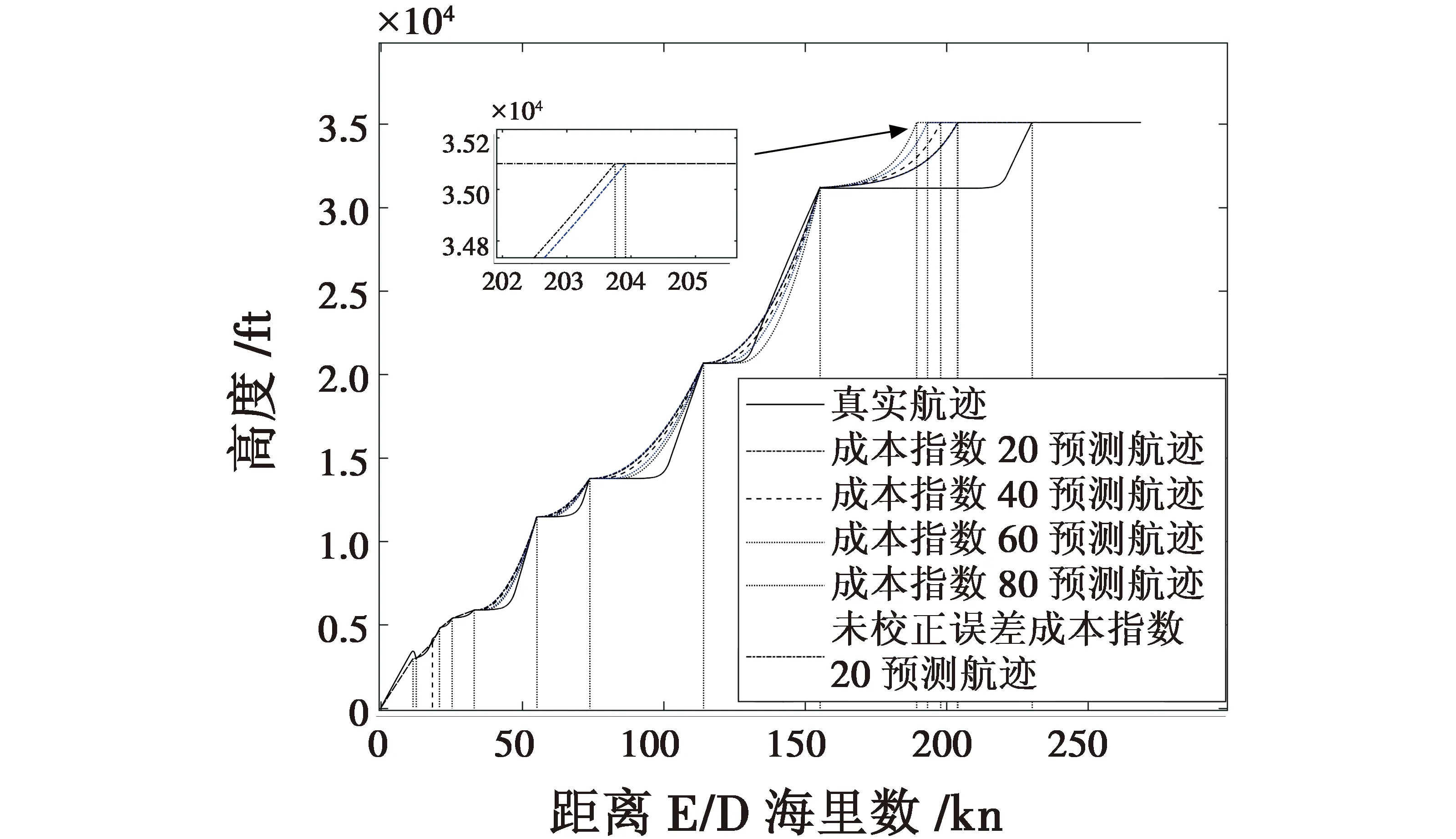
图5 不同成本指数下的仿真预测航迹Fig.5 Simulation prediction track under different CI
仿真程序根据航路点及空域限制信息对航空器下降段航迹进行预测,针对不同成本指数对航迹做出了相应优化。
为验证初始估计的E/D点航空器全重对后续仿真是否产生误差影响,更改初始估算的总燃油消耗值,在具备较大估计差异前提下仿真迭代后的预估燃油消耗量。由图6及表1可知,经由仿真迭代3次后的燃油消耗数值明显收敛。
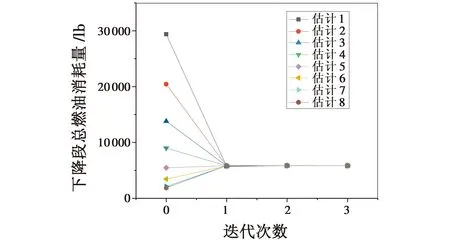
图6 初始估算对仿真的误差影响
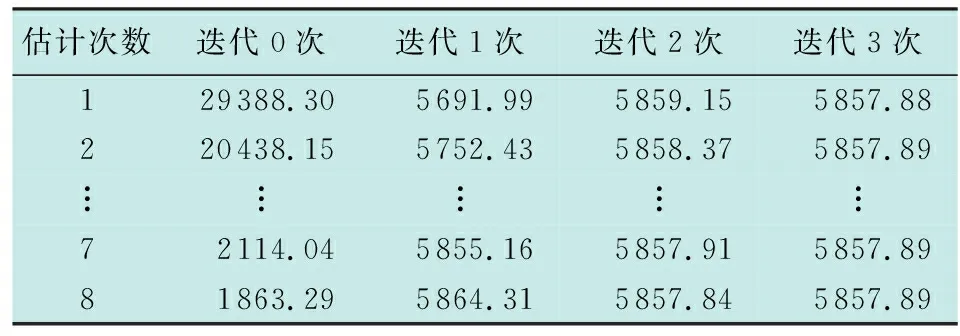
表1 初始估算及经由迭代后的下降段总燃油消耗
在仿真生成的航空器多维状态数据中选取指示空速、真空速、马赫数及发动机推力随飞行时间增加的预测数据如图7所示。
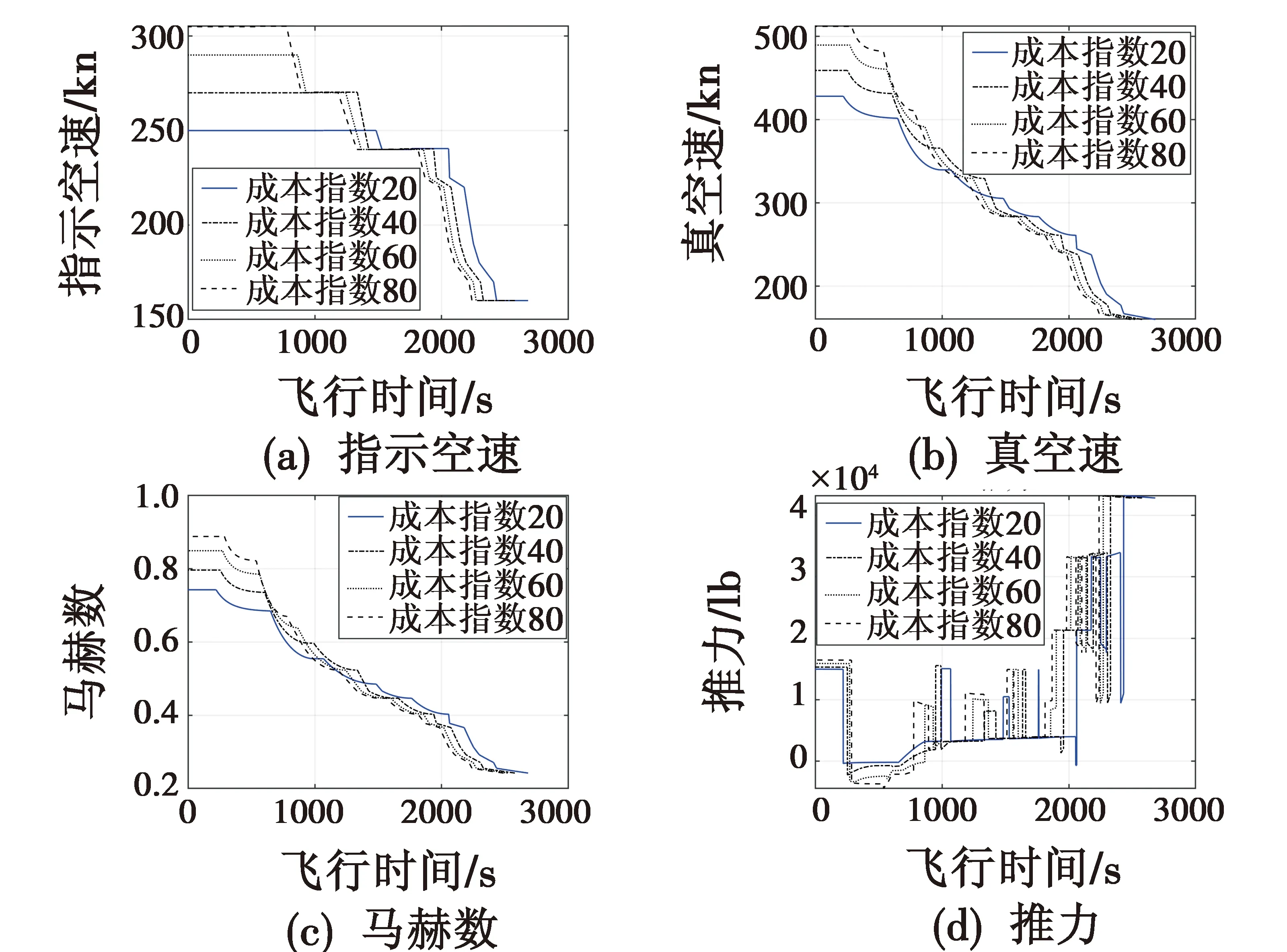
图7 航空器部分多维预测状态数据Fig.7 Part multi-dimensional forecast state data of the aircraft
为直观对比下降段真实航迹同仿真程序生成预测航迹的燃油消耗量,整理真实航迹QAR数据及多维预测状态数据中随飞行时间增加的燃油消耗量如表2及图8所示。
由表2可知,成本指数每增加20,航空器按照对应预测航迹飞行的燃油消耗平均增加1.07%,时间平均减少2.58%。
结合图5、表2及图8可知,在满足航路点限制及成本指数要求下,对比真实航迹,预测航迹在T/D以及各限高航路点位置附近减少大量平飞段,航空器根据预测航迹曲线飞行所需燃油消耗更低。如CI为40时,相比真实航迹,航空器沿预测航迹飞行的总燃油消耗量降低20.67%。
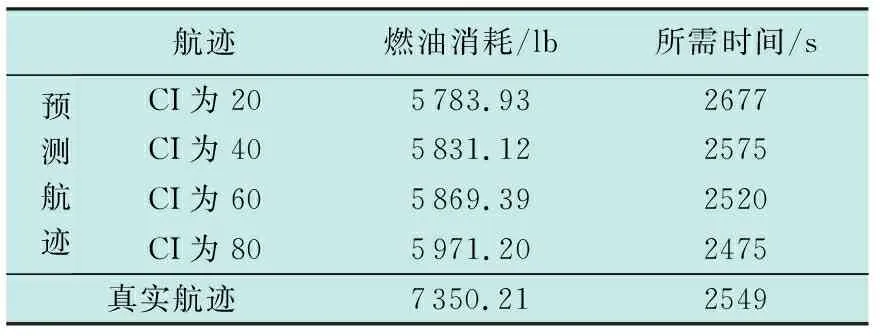
表2 下降段(T/D到E/D,高度35 100 ft至50 ft)燃油消耗与所需时间

图8 燃油消耗对比Fig.8 Comparison of fuel consumption
4 结束语
提出一种基于多目标约束的航空器下降段航迹预测方法,参考动力学应用领域深入分析航空器空气动力学及能量转换关系。通过反向积分预测航空器各状态数据,并以航路限制、成本指数以及航空器性能3个约束点构建航空器下降段航迹预测模型。最后导入航路信息、某航空器的发动机及气动参数,并进行仿真,仿真结果表明:
1) 输入某航空器相应航路数据及性能数据后,更改成本指数,模型计算并生成对应成本效益的下降航迹及航空器多维状态数据;
2) 预测航迹曲线满足下降进近阶段航路限制;
3) 对比真实航迹,航空器沿预测航迹飞行的燃油消耗更低,提高了下降阶段的燃油利用率。
由于对下降段航迹进行预测复杂多变,本文方法以动力学及能量转换为基础,加入航段信息、成本指数及性能限制的约束,反向积分迭代航空器多维预测数据,从而构建出航空器下降段的航迹预测模型。此方法同样适用于爬升、巡航段飞行路径预测,为进一步开发飞行管理仿真系统的导航模块提供理论支撑。
