六旋翼无人机编队快速终端滑模鲁棒控制

王艳丽， 孙利娟

(1.河南科技大学软件学院，河南 洛阳 471000； 2.开封文化艺术职业学院计算机学院，河南 开封 475000)

0 引言

六旋翼无人机是一种依靠控制系统按照地面站操纵指令来执行任务的飞行器，广泛应用于航拍、侦察和测绘等领域[1]。为了适应复杂且多变的任务需求，往往将多架UAV按照某种特定队形进行排列，通过UAV编队整体来执行任务[2]。其中，领导-跟随法、虚拟结构法和一致性法是最为常用的控制策略。由于领导-跟随法的结构简单、控制效果好，在UAV编队中应用最为广泛[3-4]。在实际飞行过程中，UAV容易受到不稳定气流和长机涡流的影响，严重时还会发生UAV相互碰撞的危险，威胁编队飞行安全[5]。另外，为了提高控制系统的实用性，还需要综合考虑模型误差带来的影响[6]。本文综合考虑气流扰动和模型误差下六旋翼UAV领导-跟随编队的控制方法并展开研究。

当前已有相关研究成果发表。文献[7]针对无人机集群受未知干扰影响下的编队问题进行了研究，利用有限时间干扰观测器对未知干扰进行估计，提出了一种基于误差的编队控制方法，能够确保UAV编队稳定，但是收敛条件比较严格；文献[8]针对外界干扰下的UAV分布式编队，设计了状态观测器估计UAV速度和干扰，提出了一种基于连续螺旋滑模控制的分布式编队控制器，虽然能够实现编队稳定飞行，但是响应速度较慢；文献[9]针对领导-跟随UAV编队在大气干扰下的队形保持问题，提出了一种编队模型的自适应控制方法，虽然能够保持编队队形，但是不能准确估计干扰值；文献[10]针对UAV编队飞行中的队形保持问题，提出了一种基于粒子群算法的自抗扰编队控制方法，能够实现编队飞行，但没有考虑复合干扰的影响，实用性不高。为此，本文分别针对六旋翼编队的外环模型和内环模型设计了快速终端滑模鲁棒控制律，并引入自适应律来快速、准确估计复合干扰的大小，实现了六旋翼无人机编队的安全稳定飞行。

1 建立六旋翼无人机运动模型

领导-跟随编队[11]采用的是主-从编队控制策略，在编队控制结构中，存在唯一的领导者跟随地面站指令运动，其他UAV在队形几何关系的约束下跟随领导者运动。当UAV编队规模较大时，领导-跟随法通常采用级联结构，即最上层的UAV担负领导者角色，中间层的UAV作为上层UAV的跟随者同时又作为下层UAV的领导者，层层跟随编队运动。本文研究对象为六旋翼无人机领导-跟随编队，编队拓扑结构见图1。

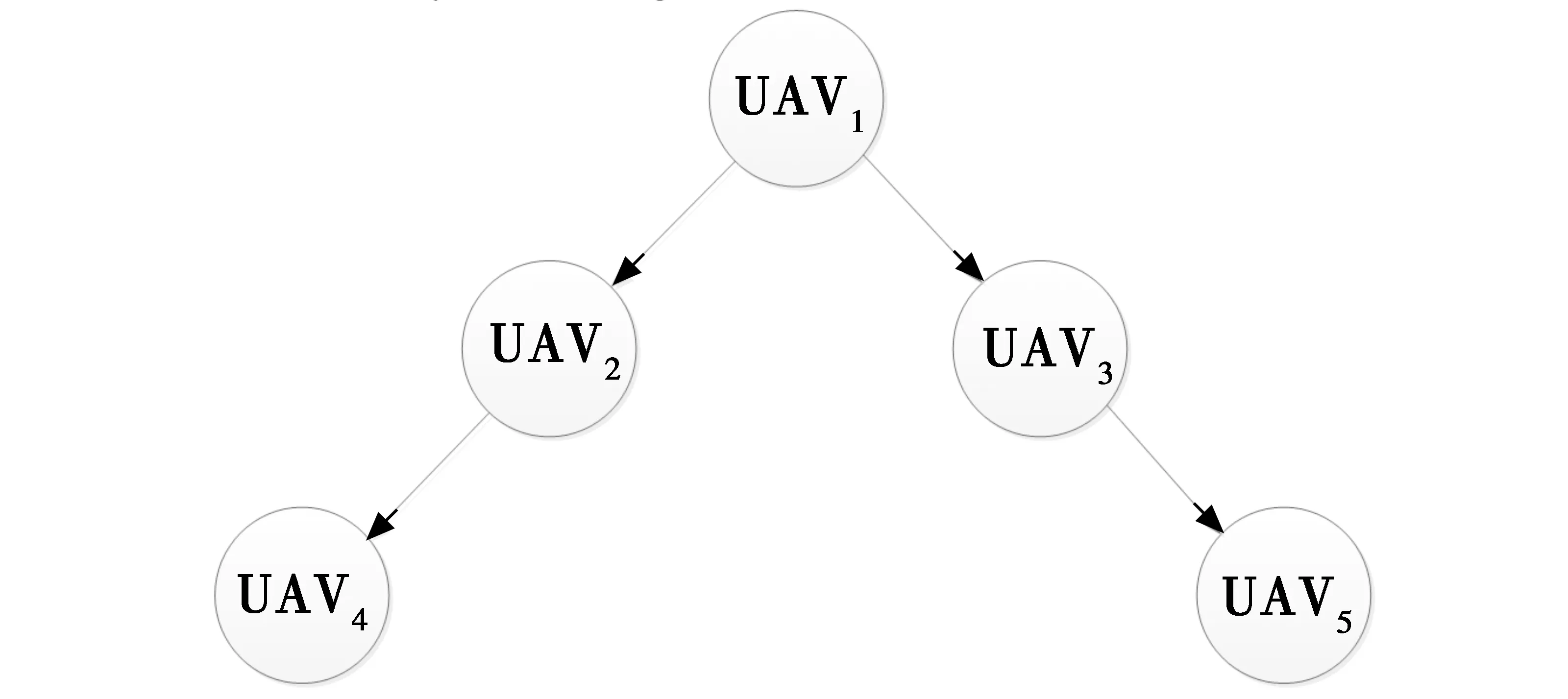
图1 编队拓扑结构Fig.1 Formation topology

图1中,UAV1是编队的绝对领导者，UAV2和UAV3跟随UAV1运动，同时领导UAV4和UAV5运动。本文中如未特别说明，变量均为标量。

六旋翼无人机是依靠6个旋翼转动来完成6自由度运动的飞行器[12]，其结构如图2所示。

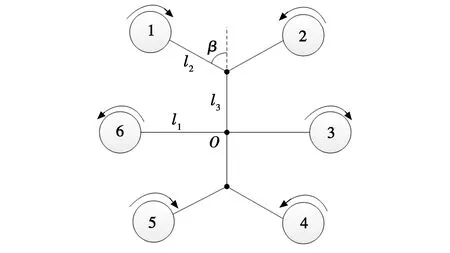
图2 六旋翼无人机结构Fig.2 Structure of six-rotor UAV

六旋翼无人机的6自由度非线性模型为[12]

(1)

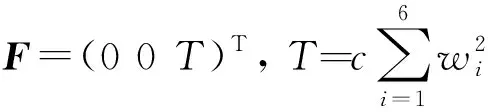
(2)

式中:b为反扭矩系数；Q为控制分配矩阵;β，l1，l2和l3的物理意义如图2所示。

在实际飞行过程中，不稳定气流会影响六旋翼无人机的正常飞行，尤其是在编队飞行中，气流扰动会使UAV相互碰撞，严重威胁编队飞行安全。另外，六旋翼无人机模型与实际UAV之间必然存在误差，会影响控制系统的实用性。综合考虑气流扰动和模型误差的六旋翼无人机模型为

(3)

式中:dv为UAV运动环的气流扰动和模型误差的复合干扰；dω为UAV姿态环中气流扰动和模型误差的复合干扰。

2 快速终端滑模控制律设计

首先根据领导-跟随编队拓扑结构得到位置指令，然后设计外环控制律解算得到姿态角指令，同时引入自适应律来估计复合干扰，最终设计内环控制律来实现UAV编队稳定飞行。以UAVi为例进行控制律设计，控制系统结构如图3所示。

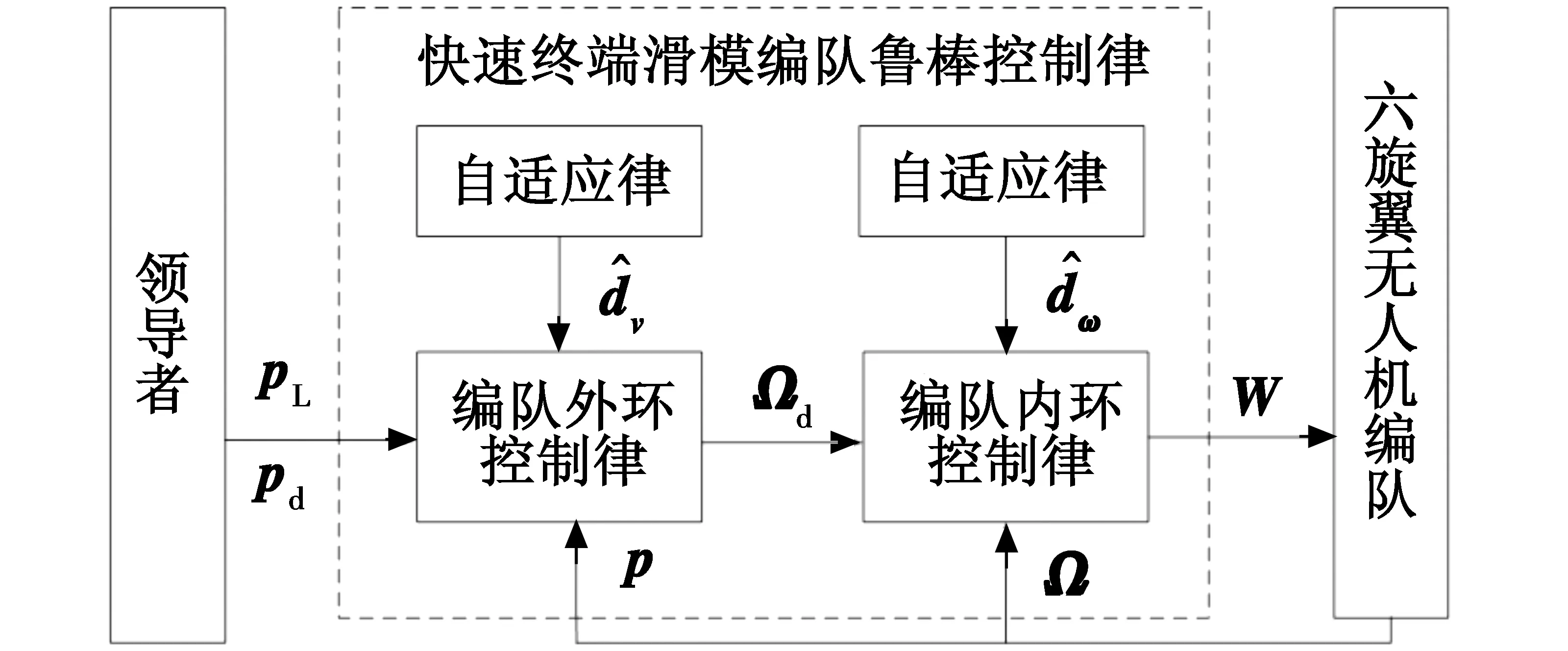
图3 控制系统结构Fig.3 Structure of control system

2.1 编队外环控制律设计

根据领导-跟随编队拓扑结构，可以得到UAVi的编队跟踪误差为

(4)

式中:pL为UAVi的领导者UAV的位置坐标，UAV1的pL为地面站发送的飞行指令；pd为UAVi与领导者UAV之间的期望距离，pd的大小决定了UAV编队的形状，且UAV1的pd为零。

对式(4)求导可以得到

(5)

构建传统滑模面为

(6)

式中，λ1为正定矩阵。传统滑模控制虽然具有一定的鲁棒性，但是动态性能较差。为了改善滑模控制的动态性能，在式(6)滑模面的基础上，提出如下快速终端滑模面

(7)

式中:k1，k2为正定矩阵；p1，q1，g1和h1是正奇数，且满足p1/q1>1，g1/h1>1。

对式(7)求导可以得到

(8)

则设计编队外环控制律为

(9)

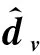
设计如下自适应律

(10)

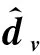
结论1 针对六旋翼无人机领导-跟随编队，设计的式(9)快速终端滑模外环控制律和式(10)自适应律，能够确保编队外环稳定。

证明过程如下。

构建如下Lyapunov函数

(11)

对式(11)求导，并将式(9)和式(10)代入化简得

(12)

则由Lyapunov稳定性定理可得结论1成立。

在六旋翼无人机中，外环控制律F与姿态角满足

(13)

由式(13)解算得UAVi的内环姿态指令[12]

(14)

式中，φLd是UAVi领导者的偏航角。

进一步可以得到UAVi所需合力T为[12]

(15)

2.2 编队内环控制律设计

定义UAVi的内环姿态误差为

(16)

式中，Ωd=(φdθdφd)T，是UAVi的内环姿态指令。

对式(16)求导可以得到

(17)

构建如下快速终端滑模面

(18)

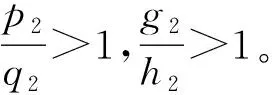
对式(18)滑模面求导可得

(19)

则可以设计编队内环控制律为

(20)

设计如下自适应律

(21)

结论2 针对六旋翼无人机领导-跟随编队，设计的式(20)快速终端滑模内环控制律和式(21)自适应律能够确保编队外环稳定。

证明过程如下。

构建如下Lyapunov函数

(22)

对式(22)求导，并将式(20)和式(21)代入化简得

(23)

则由Lyapunov稳定性定理可得结论2成立。

2.3 稳定性分析

结论3 针对六旋翼无人机领导-跟随编队，设计的式(9)快速终端滑模外环控制律和式(20)快速终端滑模内环控制律可以保证UAV编队稳定。

证明过程如下。

构建如下Lyapunov函数

W′=V1+V2

。

(24)

对式(24)求导，并将式(12)和式(23)代入化简得

(25)

则由Lyapunov稳定性定理可得结论3成立。

由式(2)可以解算得到，UAVi的旋翼转速为

(26)

3 仿真验证

为了验证本文针对六旋翼无人机编队设计的快速终端滑模鲁棒控制方法的效果，分别采用本文方法和文献[13]的领导-跟随编队滑模控制方法进行Matlab/Simulink对比仿真。

3.1 仿真参数设置

整个仿真时间为30 s，设置复合干扰dω=(costcostcost)T,dv=(costcostcost)T。六旋翼无人机编队拓扑结构如图1所示，六旋翼无人机坐标和编队指令如表1所示。

表1 编队参数与指令

六旋翼无人机编队快速终端滑模鲁棒控制律参数如表2所示。

表2 控制律参数

3.2 编队仿真分析

六旋翼无人机编队仿真结果如图4所示。由仿真结果可以看出：在文献[13]滑模控制方法的作用下，六旋翼无人机能够大致保持编队飞行，但是各UAV的运动轨迹频繁大幅波动，不能实现UAV编队稳定飞行，编队效果不好；而在本文快速终端滑模控制方法的作用下，六旋翼无人机能够克服复合干扰的影响，运动轨迹平滑稳定，可以实现UAV编队稳定飞行，编队效果较好。

图4 编队仿真结果对比Fig.4 Comparison of formation simulation results

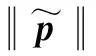
图5 编队轨迹误差对比Fig.5 Comparison of formation trajectory errors

由仿真结果可以看出：在文献[13]滑模控制方法的作用下，六旋翼无人机编队的最大轨迹误差为6 m，不能满足编队稳定飞行要求；而在本文快速终端滑模控制方法的作用下，六旋翼无人机编队的最大轨迹误差仅为0.2 m，可满足编队稳定飞行要求。

3.3 干扰估计结果

为了进一步验证本文设计的自适应律对于复合干扰的估计效果，仿真过程中施加编队外环复合干扰dv=(costcostcost)T，得到了复合干扰估计结果和复合干扰估计误差结果。

由仿真结果可看出：文献[13]的复合干扰估计结果会在真实值附近大幅振荡，估计误差在-2 m/s2～2.5 m/s2的范围波动，估计误差较大；而本文所设计的自适应律能够快速、准确地估计干扰，最大估计误差仅为0.1 m/s2。

图6 复合干扰估计结果和误差Fig.6 Estimation results and errors of compound interference

4 结束语

为了补偿不稳定气流和模型误差等复合干扰对六旋翼无人机编队飞行的影响，分别针对编队外环和编队内环设计快速终端滑模鲁棒控制律，实现编队稳定飞行。通过Matlab/Simulink对比仿真验证了提出的快速终端滑模鲁棒控制律可很好地补偿复合干扰的影响，稳定跟踪编队指令信号，最大轨迹误差仅为0.2 m，编队飞行效果较好，设计的自适应律也能够快速、准确地估计复合干扰，最大估计误差仅为0.1 m/s2，估计效果表现更优。