航班计划对延误波及变化的影响分析

闵 捷，高 强，朱勐辉

（南京航空航天大学民航学院，江苏 南京211106）

航班计划对延误波及变化的影响分析

闵 捷，高 强，朱勐辉

（南京航空航天大学民航学院，江苏 南京211106）

为了提高飞机利用率，航空公司在制定航班计划时会安排同一架飞机每天连续执行多个航班。当连续航班中的前序航班出现延误时，后续航班往往也会受到影响。为了研究航班计划对于航班延误波及传播的影响，构建了延误波及变化这一指标来反映延误波及增加或者减少的变动趋势。通过马尔科夫毯网络建立了航班计划的多个属性和延误波及变化的贝叶斯网络模型。利用列联表卡方检验揭示了航班计划中影响延误波及变化的主要因素为：相邻两个航段之间的计划过站时间和实际过站时间的差，前一个航段的航线类型，航段顺序。通过分析3个因素对于延误波及变化的影响，为航空公司控制延误波及和优化航班计划提出相应建议。

航空运输；航班计划；延误波及；马尔科夫毯网络

随着我国民航运输业的发展，航班量快速增加，航班延误问题日趋严重。除了天气、流量控制等常见原因外，航班计划的不合理也是导致航班延误的一大原因。为了提高飞机利用率、降低运营成本，在编排航班计划时，航空公司会安排同一架飞机连续执行多个航班，而且航班之间的衔接较为紧密。这种航班计划的编排方式会导致前一个航班的延误沿着航班串继续传播，最终加重后续航班的延误。基于现有的航班计划，研究延误波及在航班串中的传播规律将为下一步优化航班计划提供有益参考。

针对延误波及问题，文献[1-7]对延误波及的传播规律进行了研究，所研究的延误波及传播更多是表现在前一个航班到达延误与后一个航班起飞延误两者之间的变化上，没有直接研究延误波及的变化。文献[8]重点分析了过站时间调整量对于首发航班延误和末班航班到达延误的影响，研究了延误波及在航班串的第一个航班和最后一个航班上的变化规律，但是没有分析航班串中其余航班的延误波及变化。文献[9-10]研究了不同机场容量和空域容量对于延误波及的吸收效应，但是没有考虑飞行时间对于延误波及的影响。

为了描述一个航班串中每个航段的延误波及的具体变化趋势，本文提出延误波及变化这个指标。结合国内某航空公司的航班计划和实际数据，利用马尔科夫毯网络建立起延误波及变化的分析模型，识别航班计划中影响延误波及增加或者减少的关键因素，并分析这些因素对于延误波及变化的影响大小。结合原有航班计划，提出控制延误波及沿着航班串传播的优化建议。

1 延误波及和延误波及变化的定义

1.1 延误波及的定义

为了研究方便，这里对前序航段和后续航段做如下定义：前序航段i和后续航段j是1个航班串中2个相邻航段，2个相邻航段中靠前的航段为前序航段，靠后的航段为后续航段。

根据民航航班正常统计办法规定，在计算航班延误时间时需要考虑是否超过15min。延误波及表示了航班串中相邻的两个航段，后一个航段因为前一个航段的延误而发生的延误。由于航班串中的第1个航段前面没有航段，所以第1个航段没有延误波及，

1.2 延误波及变化的定义

如果某架飞机在执行一个航班串任务时，除了第1个航段外，余下每个航段都产生了延误波及，则这里定义一个新的指标即延误波及变化来表示延误波及增加和减少的情况。

假设航段i、航段j、航段k是1个航班串中3个相邻且依次执行的航段，航段i最先执行，则航段k相对于航段j的延误波及变化=航段k对航段j的延误波及航段j对航段i的延误波及。如果延误波及变化大于0，说明延误波及增加了；如果延误波及变化小于0，说明延误波及减少了。根据本文关于延误波及和延误波及变化的定义，从航班串中的第2个航段开始有延误波及，从航班串中的第3个航段开始有延误波及变化。

2 延误波及变化影响因素

为了研究航班计划对于延误波及变化的影响，我们从航班计划中抽出机场、飞行时间、航段顺序的相关属性，重点研究航线类型，起降时段，过站时间裕度，飞行时间裕度，航段顺序这5个与航班计划密切相关的因素对于延误波及变化的影响。

2.1 机场

机场的容量不够和保障能力不足将导致在该机场降落和起飞的航班发生延误。本文将机场按照客运量大小分为3类。其中国内繁忙机场（分类1）包括HKG、PEK、CAN等11个客运量排名国内前11的机场；国内非繁忙机场（分类2）包括XMN、CSX、WUH等客运量排名国内11名以后的国内机场；国外机场（分类3）包括BKK、BOM、CGX等全部国外机场。

前序航段的起降机场类型也将影响后续航班的延误波及。例如前序航段从繁忙机场飞到不繁忙机场发生了延误，在不繁忙机场经停之后再起飞时，后续航段可能就不再延误。为了表示每个航班在不同繁忙程度的机场之间的转移，我们定义了航线类型这个分类变量，并用每个航段的起飞机场和降落机场来表示。航线类型具体分类为：分类1（国内繁忙机场—国内繁忙机场）、分类2（国内繁忙机场—国内非繁忙机场）、分类3（国内繁忙机场—国外机场）、分类4（国内非繁忙机场—国内繁忙机场）、分类5（国内非繁忙机场—国内非繁忙机场）、分类6（国内非繁忙机场—国外机场）、分类7（国外机场—国内繁忙机场）、分类8（国外机场—国内非繁忙机场）、分类9（国外机场—国外机场）。

对于一个机场来说，不同时段起降的航班的延误情况将不同。为分析不同时段对于延误波及变化的不同影响，我们将机场一天的24个小时按照航班起降次数分为起飞特别繁忙时段（分类1）、起飞一般繁忙时段（分类2）、起飞不繁忙时段（分类3）。对于降落时段也划分为降落特别繁忙时段（分类1）、降落一般繁忙时段（分类2）、降落不繁忙时段（分类3）。

航班在一个机场的计划过站裕度也将影响到航班的延误波及变化。通常航班的计划过站时间不会设置太多冗余，即计划过站时间和实际过站时间之间的差不会太大。这就造成了当前序航班发生延误时，后续航班可能会继续延误，从而延误波及不断增加。为了评估实际过站时间和计划过站时间的差，即过站时间裕度对于延误波及变化的影响，我们定义了过站时间的差这个分类变量。过站时间的差的计算公式为：两个相邻航段之间的过站时间的差=两个相邻航段之间的计划过站时间-两个相邻航段之间的实际过站时间。如果实际过站时间小于计划过站时间，则过站时间的差为负值。将过站时间的差按照15min的间隔进行划分，分为（-∞,-60），[-60，-45），[-45，-30），[-30，-15），[-15，0），[0，15），[15，30），[30，45），[45，∞）9个区间，依次标记为分类1，分类2，……分类9。

2.2 飞行时间

通常航班计划在计算飞行时间时，会留有一定冗余，因而实际飞行时间小于计划飞行时间的情况经常发生。如果航班起飞时发生了延误，那么航班到达目的机场时延误可能减少甚至消失了，因为飞行时间冗余吸收了一部分起飞延误。为了分析飞行时间冗余对于延误波及变化的影响，我们定义了飞行时间的差这个分类变量，用来表示航班计划中每个航段的飞行时间的冗余。计算公式为：每个航段飞行时间的差=每个航段的计划飞行时间-每个航段的实际飞行时间。

本文将飞行时间的差分为（-∞,-15），[-15，0），[0，15），[15，30），[30，45），[45，∞）6个区间，依次标记为分类1，分类2，……，分类6。

2.3 航段顺序

一个航班串通常由很多航段构成。航段顺序表示每个航段在航班串中的顺序，以阿拉伯数字来进行编号。如航段顺序为5，表示该航段是航班串中的第5个航段。对于含有多个航段的航班，它的每个航段都需要按顺序依次编号。由于大部分航班串都遵从“早出晚归”的作息时间，即从早上开始执行第1个航段，最后一个航段执行完时已经接近凌晨。因此航段顺序也可以间接表示航班起飞时间的早晚。为了研究航段顺序是否会影响航段的延误波及变化，我们将航段顺序也加入模型。

3 延误波及变化的马尔科夫毯模型构建

3.1 马尔科夫毯网络

马尔科夫毯网络是贝叶斯网络的拓展。贝叶斯网络作为一种不确定性的因果推理模型，主要包括两部分：贝叶斯网络结构（有向无环图）和贝叶斯网络参数（条件概率分布）。贝叶斯网络结构是由节点和箭头组成的有向无环图，用来表示节点的相互关系。如果两个节点之间有箭头表示两个变量不是相互独立的，否则，表示两个变量相互独立。位于箭头尾部的节点是父节点，位于箭头头部的节点是子节点。贝叶斯网络参数用给定父节点取值时子节点的取值的条件概率集合来表示。

贝叶斯网络结构的构建是在初始网络结构的基础上，通过对训练样本不断学习，反复调整网络结构和参数，最终得到一个最佳网络结构用于表示变量之间的相互关系，并基于该最佳网络结构计算参数集合θxi。

3.2 马尔科夫毯网络的特点和适用范围

马尔科夫毯网络对贝叶斯网络的改进体现在增加了特征选择过程，即从众多输入变量中筛选出与输出变量显著相关的变量，去除掉不相关和冗余的变量。特征选择过程减少了学习过程的复杂度，提高了学习结果（网络结构和网络参数）的可靠性和准确性；同时最后的的网络结构只显示对于输出变量有显著影响的输入变量，简化了最后得到的条件概率的形式。对于输入变量较多的问题，采用马尔科夫毯网络可以取得较好效果。此外，马尔科夫毯网络对于输入变量是否相互独立不作要求，即输入变量彼此相关时也可以采用马尔科夫网络。

考虑到本文所选择的输入变量较多，并且变量之间不一定相互独立，加之每个输入变量对输出变量的影响不一定都很显著，本文选择了马尔科夫毯网络来建立延误波及变化的分析模型。构建马尔科夫毯网络需要确定网络结构S和估计参数θ[11]。

3.3 确定马尔科夫毯网络的网络结构S

对于马尔科夫毯网络来说，确定网络结构的核心就是寻找各变量的马尔科夫毯变量。寻找马尔科夫毯变量的过程即为特征选择过程。马尔科夫毯变量包括节点的父节点、子节点以及子节点的其余父节点。当两个变量不独立时，他们均不在彼此的马尔科夫毯变量中。马尔科夫毯网络利用卡方检验、对数似然率检验等统计学的检验方法来检验变量之间是否独立，并在此基础上构建马尔科夫毯网络结构。[11]

网络结构S的具体学习过程如下[11]：

step 1：假设起始网络结构S是一个完全连接的无向网络。

step 2：如果变量Xi和Xj独立检验的概率p-值大于指定的显著性水平a，则删除节点Xi和Xj之间的弧线。

step 3：对每个节点Xi，在余下弧线中，判断在现有网络结构S条件下，变量Xi和Xj条件独立检验的概率p-值是否大于显著性水平a，如果大于，则删除节点Xi和Xj之间的弧线。

step 4：将网络结构中的无向弧线按照图1所示的规则转换成有向弧线。

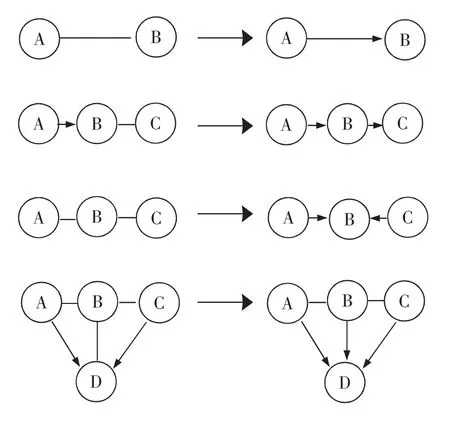
图1 马尔科夫毯网络中的弧线方向转化方式Fig.1 The transformation from undirected lines into directed lines in Markov Blanket Network

3.4 估计马尔科夫毯网络的参数θ

马尔科夫毯网络采用贝叶斯方法来进行各节点的参数估计，各节点的参数彼此独立。1个节点的参数θ的估计，涉及到了先验概率、似然函数和后验概率。当变量具有2个以上分类时，参数θ的先验分布和后验分布都选用Dirichlet分布，参数θ的先验分布的数学形式为

式中：Γ（a1+a2+…+ar）为Gamma函数；r为每个变量的类别数；a1，a2，…，ak…，ar是Dirichlet分布的超参数；θ是0～1之间的某个值；Dir（θ|a1，a2，…，ar）表示Dirichlet分布。

参数θ的后验分布的数学形式为

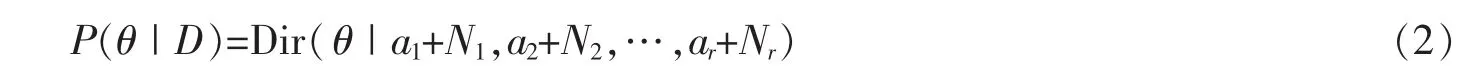
式中：r为每个变量的类别数；D为给定样本数据；N1，N2，…Nr是一个变量每个类别出现的频数。基于Dirichlet分布，变量的取类别k的参数θr的最终估计值为

式中：N为训练样本的数据量；Nk为变量取类别k的数据量。

当得到最优的网络结构时，也会得到了每个子节点相对于其父节点集合的条件概率。再根据贝叶斯公式，便可以计算每个子节点相对于某一个父节点的精确条件概率。

4 实例分析

我们选取了国内某航空公司2015年1月的航班计划和实际运营数据，经过筛选、清洗等预处理后，得到了13 449条有效数据。对数据按照前文所述方法进行离散化处理，得到了包含输入变量和输出变量的数据集见表1。表1中的航段i和航段j表示航班串中的两个相邻航段，航段i在航段j前面。

将上述数据集输入马尔科夫毯网络进行贝叶斯网络结构学习，得到初始网络结构如图3所示。本例采用对数似然率检验方法来进行两个节点的独立性检验，显著性水平a=0．01。节点Xi取类别k对应的超参数为本节点的类别数，si为本节点所有父节点的全部类别的组合数）。按照前文所述的网络结构学习过程，经过多次学习，最终得到网络结构如图3所示，同时得到每个节点的后验概率。图2和图3中的航段i和航段j表示航班串中的两个相邻航段，航段i是航段j的前一个航段。根据马尔科夫毯网络有关知识，如果输入变量对于输出变量（延误波及的变化）的影响较小，则不会出现在图3中。

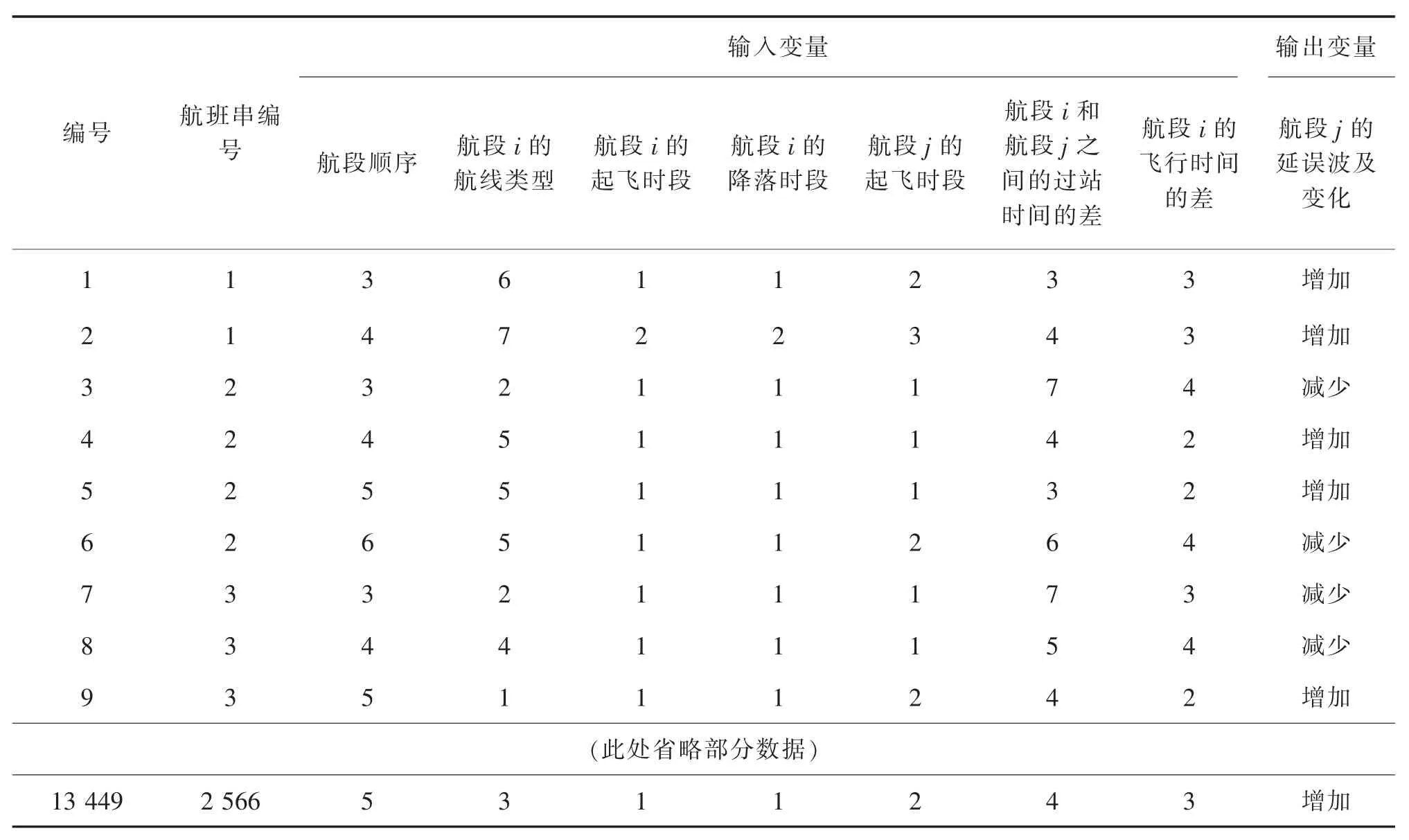
表1 包含输入变量和输出变量的数据集Tab.1 Dataset of input variables and output variable

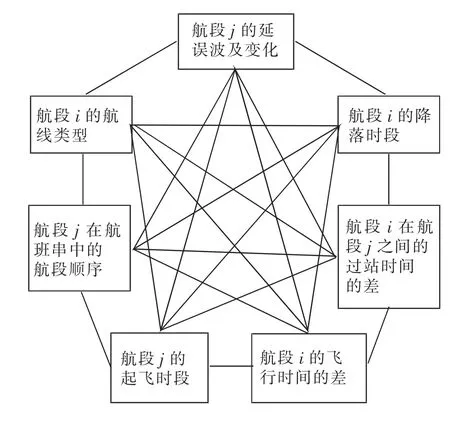
图2 初始的马尔科夫毯网络Fig.2 Initial diagram of Markov Blanket Network

图3 最终的马尔科夫毯网络Fig.3 Final diagram of Markov Blanket Network

4.1 影响延误波及变化的主要因素

从图3可以看出航段j的延误波及变化主要受到航段i和航段j之间的过站时间的差、航段i的航线类型、航段j在航班串中的航段顺序3个因素的影响。为了判断这3个因素中的重要性，我们对这3个因素和延误波及变化使用了列联表来进行卡方检验，检验结果见表2。根据卡方检验有关理论，Cramer’s V系数和相依系数越大，说明两个变量之间的相关性越强。根据表2的结果，可以推断出航段i和航段j之间的过站时间的差是对延误波及变化影响最大因素，其次是航段i的航线类型、航段j在航班串中的航段顺序。

表2 列联表检验结果Tab.2 Test result of contingency tables

4.2 航段i和航段j之间的过站时间的差对延误波及变化的影响

通过马尔科夫毯网络，我们可以得到当延误波及的变化分别为增加、减少两种情况下的过站时间的差的条件概率，具体见表3。从表3我们可以得到，当航段j比航段i的延误波及增加时，相邻两个航段的计划过站时间比实际过站时间少15～30min时的概率最大，为35%；当航段j比航段i的延误波及减少时，相邻两个航段的计划过站时间比实际过站时间多15～30min的概率最大，为33%。因此如果该航空公司希望减少后续航班的延误波及，可以考虑将计划过站时间再延长15～30min，这样可以在一定程度上控制后续航班的延误波及的加重。

表3 相邻两个航段之间的过站时间的差的条件概率Tab.3 Conditional probability of connection time difference between two successive legs

4.3 航段i的航线类型对延误波及变化的影响

由马尔科夫毯网络得到了航段i的航线类型在延误波及增加和减少两种情况下的条件概率，具体数据见表4。从表4我们可以发现，当航段j比航段i的延误波及增加时，航段i的航线类型是“国内繁忙机场—国内繁忙机场”和“国内非繁忙机场—国内繁忙机场”的概率较大，分别为36%和31%；当航段j比航段i的延误波及减少时，航段i的航线类型是“国内繁忙机场—国内非繁忙机场”和“国内非繁忙机场—国内非繁忙机场”的概率较大，分别为30%和26%。因此航空公司在安排航班串时，应该尽量避免两个相邻航段的起降机场都是国内繁忙机场，可以考虑将其中的某个国内繁忙机场替换为国内非繁忙机场，这样可以在一定程度上避免延误波及的加重。

表4 前序航段航线类型的条件概率Tab.4 Conditional probability of previous leg’s route

4.4 每个航段的航段顺序对延误波及变化的影响

考虑到当航班串的航段总数不同时，航段顺序的意义不一样，我们选取了数据集中占比最高的3类航班串，即航段总数分别为4，5，6的3类航班串来分析航段顺序对于延误波及变化的影响。这3类航班串的数量占总数的比例分别为31%，18%，35%。

表5～表7是当航班串的航段总数分别为4～6，延误波及增加或者减少时航段顺序的条件概率。可以看到对于航段总数为4的航班串，延误波及增加多发生在航段顺序为3的航段，延误波及减少多发生在航段顺序为4的航段；对于航段总数为5的航班串，延误波及增加多发生在航段顺序为3的航段，延误波及减少多发生在航段顺序为5的航段；而对于航段总数为6的航班串，延误波及增加多发生在航段顺序为3和4的航段，延误波及减少多发生在航段顺序为5和6的航段。这表明对于航段总数为4～6的航班串，延误波及增加多发生在航班串的前面几个航段，延误波及减少多发生在航班串的后面几个航段。航段顺序可以间接表示航班起飞时间的早晚。对于旅客来说，考虑到出行方便性，通常不会选择较晚起飞的航班（即航段顺序靠后的航班）。对于航空公司来说，可以利用较晚起飞的航班延误率较低这一优势，通过降低票价等营销手段来吸引更多旅客乘坐航段顺序靠后的航班，从而提高旅客的满意度。

表5 每个航段的航段顺序的条件概率（航班串的航段总数为4）Tab.5 Conditional probability of every leg’s order(for flight-stringsw ith 4 legs)

表6 每个航段的航段顺序的条件概率（航班串的航段总数为5）Tab.6 Conditional probability of every leg’s order(for flight-stringsw ith 5 legs)

表7 每个航段的航段顺序的条件概率（航班串的航段总数为6）Tab.7 Conditional probability of every leg’s order(for flight-stringsw ith 6 legs)

5 结论

本文从航班计划出发，提取了航班计划的部分属性，利用国内某航空公司的航班计划和实际运行数据，建立了这些属性和延误波及变化的马尔科夫毯网络模型。我们发现航班计划中对延误波及变化有较大影响的因素为相邻两个航段之间的过站时间的差、前序航段的航线类型、航段顺序，并得出了当延误波及增加、减少时上述3个因素的条件概率。通过分析3个因素对于延误波及变化的影响，为航空公司控制延误波及和优化航班计划提出相应建议。

引起航班延误波及变化的因素除了航班计划外，还有天气、流量控制等多方面因素，本文仅仅研究了航班计划对于延误波及变化的影响，未考虑其他因素，存在一定局限性。如何建立一个包括航班计划、天气、流量控制等多个因素的更完善的模型来研究延误波及的传播和变化，是下一步研究的重点。

[1]刘玉洁，何丕廉，刘春波，等.基于贝叶斯网络的航班延误波及研究[J].计算机工程与应用，2009，44（17）：242-245.

[2]徐涛，丁建立，王建东，等.基于贝叶斯网络的航班延误与波及分析模型[J].系统仿真学报，2009，21（15）：4818-4822.

[3]曹卫东，贺国光.连续航班延误与波及的贝叶斯网络分析[J].计算机应用，2009，29（2）：606-610.

[4]WONG JT，TSAISC.A survivalmodel for flight delay propagation[J].Journal of Air TransportManagement，2012，23：5-11.

[5]邵荃.基于贝叶斯网络的机场航班延误因素分析[J].科学技术与工程，2012，12（30）：8120-8124.

[6]吴薇薇，孟亭婷，张皓瑜.基于机场延误预测的航班计划优化研究[J].交通运输系统工程与信息，2016，16（6）：189-195.

[7]李鹏.航班延误分析及传播机理研究[D].南京：南京航空航天大学，2016.

[8]曹卫东，林翔宇.基于贝叶斯网络的机场过站时间分析[J].航空计算技术，2010，40（5）：5-9.

[9]CHURCHILL A，LOVELLD，BALLM.Flight delay propagation impacton strategic air traffic flowmanagement[J].Transportation Research Record:Journal of the Transportation Research Board，2010（2177）：105-113.

[10]ARIKAN M，DESHPANDE V，SOHONIM.Building reliable air-travel infrastructure using empirical data and stochasticmodels of airline networks[J].Operations Research，2013，61（1）：45-64.

[11]薛薇.基于SPSSModeler的数据挖掘[M].2版.北京:中国人民大学出版社，2014：324-327.

Influence Analysis of Flight Schedule on Delay Propagation Variation

Min Jie,Gao Qiang,Zhu Menghui
（College of Civil Aviation,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China）

To improve the utilization rate of airplanes，airline companiesmay arrange for an airplane to performmultiple flights every day whenmaking flight schedules.Amid sequential flights，subsequent flights are bound to be influenced by previous delayed flights.To evaluate the impacts of flight schedule on the flight delay propagation,an index of was proposed to reflect the increasing or decreasing tendency of delay propagation.A Markov Blanket Network was establishay，in cludingmultiple attributes of flight schedules.Major factors influencing delay propagation variation of flight scheduleswere analyzed by using chi-square of contingency tables：the difference between scheduled connection time and actual connection time，the types of previous flight route and the orders of legs.The research shows that the analysis of the threemajor factors provides airline companies with some suggestions for controlling delay propagation and optimizing flight schedules.

air transport；flight schedule；delay propagation；Markov Blanket Network

1005-0523（2017）05-0081-08

TP18

A

2017－05－04

中央高校基本科研业务费重点项目（NZ2016109）

闵捷（1986—），女，硕士研究生，研究方向为交通运输系统优化。

高强（1973—），男，副教授，博士，研究方向为交通运输系统优化。

（责任编辑 姜红贵）