基于小波包-Copula互信息的肌间耦合特性*

金国美佘青山*马玉良张建海孙明旭

(1.杭州电子科技大学自动化学院(人工智能学院)，浙江 杭州 310018；2.浙江省脑机协同智能重点实验室，浙江 杭州 310018；3.济南大学自动化与电气工程学院，山东 济南 250022)

人体运动是在中枢神经系统控制下完成的复杂过程。运动过程中，中枢神经系统通过神经振荡的方式将运动控制信息传递到相关的肌肉块，引起运动单元的振荡活动[1]，表面肌电信号(surface Electromyographic，sEMG)包含中枢神经系统控制的众多运动单元的动作电位信息[2]，肌肉间不同时空层次的耦合关系体现了运动过程中相关肌肉间的相互作用和相互联系[3]。因此，研究运动过程中sEMG信号间不同频段下的耦合特性，有助于理解中枢神经系统控制下肌肉间的信息传递和耦合作用。sEMG信号耦合分析在近年来成为许多学者研究的热点，为运动医学和康复工程等领域提供理论依据[4]。

日常生活中，人们在进行运动时会随着运动时间的增加而产生疲劳，从而停止运动。但是，患者在进行康复运动时，由于患者的急切康复心理和对肌肉承受力的主观感知延缓性而导致过度训练，造成二次损伤，严重的还会导致终身残疾。然而，现有的康复技术无法实现有效检测肌肉在不同时期状态的功能。目前，肌肉疲劳研究大多数是基于生物电信号，其中sEMG信号是研究肌肉疲劳状态中较为客观准确且无创的生理反馈信号[5]。Cui等[6]利用sEMG信号的特征来对训练期间球员肌肉疲劳进行分类，分类准确率可达95%以上；Wang等[7]提出了快速细化的复合多尺度样本熵方法用于分析等距收缩活动中肱二头肌的疲劳过程，发现疲劳与非疲劳之间存在显著差异。Yu等[8]研究旋转手时上肢肌肉之间的疲劳变化，发现在不同的旋转角度下，肌肉疲劳的特征是不同的。

自1999年Brown等[9]发现了运动过程中sEMG信号之间具有一定关系以来，相继有研究者对肌电信号之间的耦合关系展开研究，取得了一定的研究成果。Nguyen等[10]发现不同的运动范式具有不同的肌间耦合关系，且不同频段的肌间耦合强度也有所不同。王洪安等[11]利用相干性分析方法探究健康人与卒中患者协同肌的耦合强度差异。黄威等[12]利用广义偏定向相干分析方法探究多块肌肉之间的信息传递关系和不同握力下的肌间耦合特性。相干性、格兰杰因果等传统的耦合分析方法只能描述线性的耦合关系，并且相干性分析方法计算出的耦合强度有所偏高[13]。互信息(Mutual Information，MI)是一种用来衡量两个随机变量之间关联程度的方法，其值越大，表明两者之间关联程度越高。MI在研究中广泛应用于非线性耦合分析[14]。陈玲玲等[15]利用MI分析肌间关联特性，构建上肢肌肉功能网络。然而，MI的估计是在准确表示联合概率密度函数的前提下进行的，这在实际情况下通常难以实现。Ma等[16]通过Copula函数估算MI解决了联合概率密度函数精确表示的问题，证明了MI可以等价为Copula熵。在此基础上，Ince等[17]提出了高斯Copula互信息(Gaussian Copula Mutual Information，GCMI)方法，不需要假设每个变量的边际分布，且计算效率高。

由于sEMG信号频域特征突出，在不同特征频段上的耦合特性具有差异。肌间耦合突出表现在alpha(8 Hz～15 Hz)频段、beta(15 Hz～30 Hz)频段和gamma(30 Hz～60 Hz)频段。Copula互信息是时域上的计算，不能描述频域信息，因此，研究者采用小波分解方法对sEMG信号进行分解。Charissou等[18]结合小波与相干分析方法，分析不同频段下的肌间耦合特性，发现不同运动下的beta频段耦合特性具有差异。Yang等[19]将小波分析与相干分析相结合分析单次实验脑肌电的耦合特性。然而，小波变换存在频率分辨率会下降的缺点。因此，引入小波包(Wavelet Packet Transform，WPT)分解方法，小波包是小波的延伸，对信号分解更加精细，并且该分解方法具有无冗余、无疏漏，一定程度上提高信号的频率分辨率，在生物医学信号的时频分析方面具有广泛的应用[20]。

为了准确定量描述不同频段的肌间耦合强度，本文将小波包分解与Copula互信息相结合，构建小波包-Copula互信息模型，并应用于肘关节屈曲运动中的肌间耦合分析。首先对sEMG信号进行预处理，其次用小波包对处理过的sEMG信号进行分解，然后计算不同频段的肌间耦合强度，得到不同频段的肌间功能耦合特性。通过该分析模型可以定量描述在疲劳前后状态下肘关节屈曲运动中的协同肌肉对与拮抗肌肉对的特征频段的耦合特性，为进一步探究肌肉疲劳的神经控制机制提供新的研究方法。

1 数据采集及预处理

1.1 数据采集

实验数据包含5名健康成年人，年龄21～25岁，体重50 kg～70 kg，身高165 cm～175 cm，所有受试者均无上肢运动功能障碍或关节损伤历史，均为右利手。所有受试者精神状态良好，都被告知了实验详情，签署了知情同意书，自愿参加此次数据采集实验。sEMG信号采集装置为美国Delsys公司生产的TrignoTMWireless sEMG，采样频率为1 926 Hz。根据生理学知识，本实验同步记录与肘关节屈曲动作密切相关的三块肌肉，分别为:肱三头肌(Triceps-Brachii，TB)、肱桡肌(Brachioradialis，B)、肱二头肌(Biceps Brachii，BB)。在实验前需要用酒精清洁受试者被采集的皮肤表面，以减少阻抗，避免其对信号采集的影响。根据解剖学知识找到运动所对应的肌肉放置传感器，用绷带包裹传感器使其紧贴肌肉，避免运动导致的伪影，sEMG信号采集位置和实验环境如图1所示。为了增强肌肉活动，使肌肉快速达到疲劳状态，受试者手持哑铃，进行上肢肘关节屈伸运动。实验在安静的室内环境下进行，受试者根据节拍器匀速地进行肘关节运动，每次实验一直持续运动到受试者示意疲劳或观察到手肘剧烈颤抖结束，休息30 min，重复该过程，每位受试者进行三次实验，在实验开始受试者运动5 s后，才开始记录数据，整个实验流程如图2所示。

图1 sEMG信号采集位置和实验环境

图2 实验流程图

1.2 数据预处理

由于动作电位通过多层生物组织传导，记录到的sEMG信号很微弱且不平稳，容易受外部环境影响，为减少干扰并获取更有效的sEMG信号进行下一步肌间耦合分析，需要对采集的sEMG信号进行预处理。实验采集的信号均依次进行去均值、去除基线漂移，并进一步利用滤波器抑制50 Hz工频干扰，然后用带通滤波器对其进行0.5 Hz～200 Hz的带通滤波。以一位受试者为例，预处理后频域图如图3所示。

在sEMG信号采集的实验中，不同的受试者会有不同的振幅，每个受试者进入疲劳状态的时间也不同，这些差异与受试者的身体素质有关。本文采集肌肉分别处于疲劳前状态和疲劳后状态的20 s信号。从图3可知，与疲劳前状态相比，疲劳后状态显示出较高的幅值。

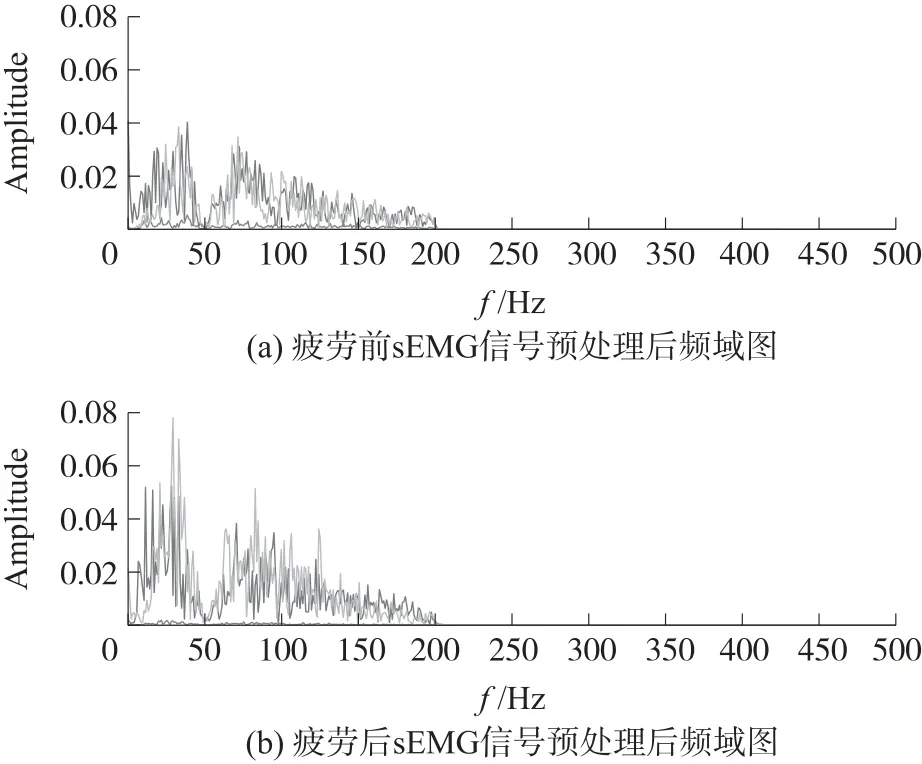
图3 sEMG信号疲劳前后的频域图

2 sEMG肌间耦合分析

为研究肘关节屈曲运动特征频段上的肌间耦合特性，构建小波包-Copula互信息耦合分析模型，应用于肘关节屈曲运动中的sEMG信号分析。首先，利用小波包将sEMG信号进行分解，获得sEMG信号在不同频段上的信息，然后用Copula互信息分析方法，计算特征频段的肌间Copula互信息值，定量研究在疲劳前后状态下的协同肌对和拮抗肌对的功能耦合特性。

2.1 小波包分解

为了得到sEMG信号在特征频段的信息，小波包分解需要选取合适的小波包函数和相应的分解层数。定义肌电信号为X(t)，通过小波包分解，设置该肌电信号的分解层数为i，将(0，2-1fs)频段内的信号分解获得2i个子带信号，并且每个子带信号对应的频段为((n-1)2j-1fs，n2j-1fs)，n＝1，2，…，2i，j＝-i，其中n代表节点数，则该肌电信号X(t)在第i层的第n个子带信号定义为:

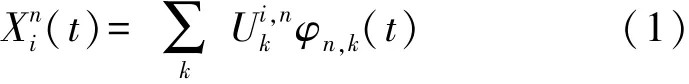
式中:i，k，n∈Ζ，为第i层的第n个子带小波包系数，φn，k(t)为小波包函数，代表特定频段的数据信息。

小波包的分解结构如图4所示。原始信号通过小波包逐级向下分解。从根节点开始，每个节点的信号都经过低通和高通滤波(每一层左边的节点是对上一节点的低通滤波，右边的节点是对上一节点的高通滤波)后再进行一个2倍向下采样的过程，实为降低采样率，只保留偶数序号的元素。经过小波包分解，其子频带乱序排列，需要翻转所有经过高频滤波并下采样的分量的频谱顺序，从而保证分解得到的子频带按升序排列(从左到右依次递增)。例如，输入信号采样频率为128 Hz，则小波包根节点(0，0)处的频率为0 Hz～64 Hz，第3层8个节点的频谱分布为:(3，0)节点代表0～8 Hz，(3，1)节点代表8 Hz～16 Hz，后面以此类推，每个节点代表一个频段，依次以8 Hz为一个频段递增，(3，7)节点代表56 Hz～64 Hz。

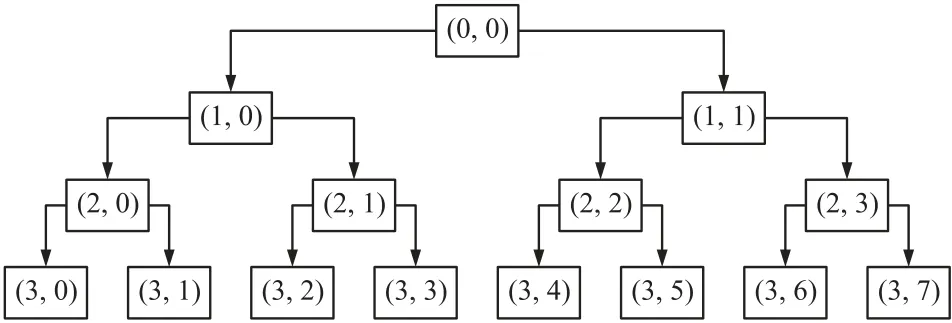
图4 3层小波包分解结构

2.2 小波包-Copula互信息的肌间耦合分析

首先，基于2.1节中分解得到的sEMG信号子带分量，然后利用Copula互信息进行分频段的肌间耦合分析，具体如下。

设X和Y分别表示两通道sEMG信号经过小波包分解得到的频谱能量集中在相同频段的分量，变量X，Y之间的MI定义如下:

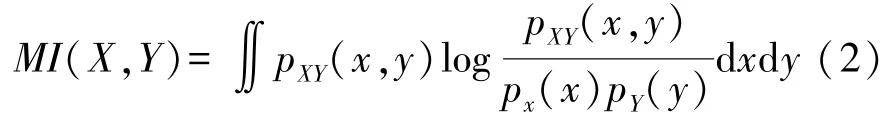
式中:p XY(x，y)表示变量X和Y的联合概率密度，p x(x)和p Y(y)分别为变量X和Y的边际概率密度函数。

由二元Copula的Sklar定理[21]可知:

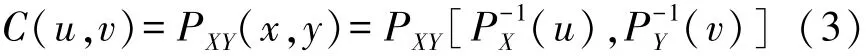
式中:P XY(x，y)表示变量X和Y的联合累积分布函数，u＝P X(x)和v＝P Y(y)分别为变量X和Y的边际累积分布函数。可推导出Copula密度函数:

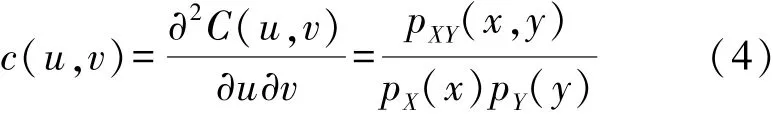
Copula熵的定义[22]如下:

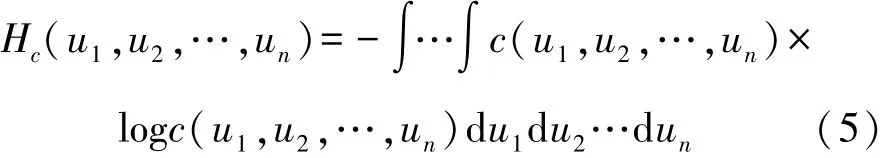
根据文献[23]，MI与Copula熵存在以下关系:

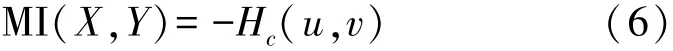
式中:H c(u，v)为变量X和Y的Copula熵。式(6)所得到的MI称为Copula互信息，它的值越大，变量的相关性越大。它是通过Copula函数得到MI的估计值，不同的Copula函数所得到的Copula互信息估计值不相同。为了获得更加准确的估计值，Copula函数的选择至关重要。常见的Copula函数有Gaussian Copula、t Copula、Clayton Copula、Frank Copula和Gumbel Copula。选择的关键在于要确定数据的边际分布类型，本文采用非参数核密度估计不同频段分量的边际分布，根据最大似然函数准则选择最佳的Copula函数，从而估计Copula互信息。

3 实验的结果

sEMG信号不同频段内的耦合特性反映中枢神经系统的支配信息。本文构建了小波包-Copula互信息模型，研究肘关节屈曲运动中的协同肌对和拮抗肌对在不同频段的肌间耦合特性，探究在疲劳前后状态下的协同肌肉对和拮抗肌肉对的肌间耦合特性。

3.1 协同肌肉对与拮抗肌肉对的肌间耦合特性分析

根据1.1节中的实验范式同步采集与肘关节屈曲运动密切相关肌肉块的sEMG信号，其中BB与B为协同肌对、BB与TB为拮抗肌肉对。将采集的sEMG信号进行预处理，利用小波包分解得到特定功能频带的信号，分别对疲劳前后的BB-B与BBTB进行独立频段肌间耦合分析。图5为受试者2(其他受试者的结果与此相似)在疲劳前后状态下的BB-B与BB-TB在alpha、beta和gamma频段的肌间耦合强度。由图5可见，BB-B与BB-TB在alpha、beta和gamma频段的肌间耦合强度表现为频段越高，耦合强度越大。协同肌肉对与拮抗肌肉对在beta和gamma频段表现出较强的耦合关系。另外，不管受试者是处于疲劳前还是疲劳后的状态，协同肌肉对的耦合强度明显高于拮抗肌肉对的耦合强度。

图5 疲劳前后的肌间耦合强度

3.2 疲劳前后的肌间耦合特性分析

为了探究疲劳因素对于肌间耦合强度的影响，本文进一步比较疲劳前与疲劳后状态的耦合特征，分别对BB-B与BB-TB在疲劳前与疲劳后状态下进行不同特征频段肌间耦合分析。图6为受试者4(其他受试者的结果与此相似)BB-B与BB-TB在疲劳前后状态下的alpha、beta和gamma频段的肌间耦合强度。由图6可见，疲劳状态下BB-B的beta和gamma频段的肌间耦合强度明显高于疲劳前状态下对应的频段耦合强度，而BB-B的alpha频段与BB-TB的alpha、beta和gamma频段在疲劳前后的差异不显著；疲劳状态下的B-BB与BB-TB整体的耦合强度相比于疲劳前有所增强，且相比于BBTB，B-BB疲劳前后耦合强度的增加更为明显。

3.3 肌间耦合差异的统计分析

为了分析上述现象是否具有统计学意义，定量地描述特征频段耦合强度的差异，对所有受试者B-BB与BB-TB在疲劳前后状态的alpha、beta和gamma频段的耦合强度取平均与方差，并对各个频段在不同情况下的耦合强度进行独立样本t检验，结果如图7所示。无论受试者处于疲劳前还是疲劳后状态，协同肌肉对在alpha、beta和gamma频段的耦合强度明显大于拮抗肌肉对的耦合强度；对比疲劳前和疲劳后，疲劳后的协同肌肉对在beta和gamma频段的耦合强度明显高于疲劳前，而拮抗肌肉对的耦合强度相对较弱且在alpha、beta和gamma频段的疲劳前与疲劳后的耦合强度无显著性差异。通过整体对比可以发现，相比于拮抗肌肉对，协同肌肉对的肌间耦合强度更大；疲劳后状态相比于疲劳前状态，肌间耦合强度增大，且协同肌肉对的变化比拮抗肌肉对更加显著。

图7 所有受试者在疲劳前后、协同与拮抗肌肉对在特征频段耦合强度的均值与方差

4 讨论

自主运动引起的肌肉疲劳是一种常见的神经生理现象。本文研究肘关节屈曲运动过程中疲劳前后状态下协同肌肉对与拮抗肌肉对在特征频段下的耦合关系，探索中枢神经系统对肌肉的控制机制。

协同肌肉对与拮抗肌肉对特征频段的耦合存在差异。协同肌肉对和拮抗肌肉对在beta和gamma频段表现出较强的耦合关系，这与运动过程中神经肌肉系统的调控有关。其中beta频段能反映运动皮层到运动神经元控制信息的传递，是中枢神经系统运动控制的重要频段[24]，gamma频段的耦合体现在与肌肉收缩和认知过程相关的信息整合[25]。这与文献[26]中得出的结论一致。协同肌肉对的整体耦合强度相对于拮抗肌肉对更高，这与文献[27]所得出的结果一致。这可能是因为中枢神经系统对发挥不同作用的肌肉对采取不同的调控策略。相较于拮抗肌肉对，协同肌肉对需要更多的控制信息[28]。谢平等[29]在研究腕部屈伸肌间的协同-耦合关系时指出，协同性较高的肌肉间耦合关系较强，不具有协同性的肌肉间的耦合关系较弱。

协同肌肉对与拮抗肌肉对在疲劳前后特征频段的耦合强度存在差异。疲劳状态下的BB与B在beta和gamma频段的耦合强度相较于疲劳前显著增加，B-BB与BB-TB疲劳后的整体耦合强度都大于疲劳前，肘关节屈曲过程中伴随着BB的收缩和TB的松缓，BB与B为协同肌，B也会收缩，当运动时间增长，肌肉块逐渐呈现疲劳状态，为了控制相应的肌肉块来维持运动，中枢神经系统要调节相关肌肉的支配方式，传递更多的运动控制信息，使得皮层神经元与运动元之间的同步耦合性增强。这符合肌肉的疲劳程度与肌电一致性存在正相关的结论[30]，并且与文献[31]和文献[32]中的结果相似。杜义浩等[33]的研究结果表明，在低负荷持续疲劳过程中，协同肌肉对与拮抗肌肉对的耦合强度都增加。协同肌肉对的耦合强度变化更为显著，可能由于在疲劳状态下中枢神经系统对两组肌肉对采取不同的控制方式。

为进一步验证该方法的有效性，可以从以下方面进行研究:采集更多健康受试者的数据进一步验证该分析方法；数据的采集从健康人拓展到运动功能障碍患者；可以添加脑电数据，从脑肌电耦合、肌间耦合等多层次深入研究，为肌肉疲劳的控制机制与康复运动功能评价方法提供新的方法和参考指标。

5 结论

本文提出了小波包分解-Copula互信息方法，并应用其分析健康人恒定负荷下的sEMG信号同步耦合特性。结果表明:在肘关节屈曲运动中，肌间耦合强度在beta与gamma频段最为显著，协同肌肉对耦合强度比拮抗肌肉对耦合强度大；疲劳后的耦合强度相对于疲劳前有所增强。因此，本文提出的小波包分解-Copula互信息分析方法可以量化评价协同肌肉对与拮抗肌肉对信号在疲劳前后特征频段肌间耦合强度，为探索人体运动功能控制机制及运动功能障碍产生机理提供理论依据。