基于学生t分布的变分贝叶斯UKF算法在无人船对准中的应用

黄 臻吴 峻

(东南大学 微惯性仪表与先进导航技术教育部重点实验室，江苏 南京 210096)

初始对准是捷联惯导系统导航精度的关键之一。对于低精度惯导系统或系泊状态下无人船的粗对准误差较大，会出现大失准角的情况，SINS误差模型具有较强的非线性[1]。并且无人船无人的特性使其相比传统舰船更适合在环境更加复杂和恶劣的场景下完成作业，因此无人船在恶劣海况下的精对准往往是大失准角的对准。在恶劣海况下无人船会产生大幅摇摆，同时还会受到浪涌、阵风等复杂未知干扰，噪声往往具有时变特性，且由于传感器本身的误差和干扰噪声等的影响，量测输出往往含有部分野值，量测噪声不满足高斯分布而具有“厚尾”特性。针对这一问题，学者们在传统算法的基础上研究提出了很多改进算法。受到广泛应用的一类算法是以Sage-Husa为代表的对噪声统计特性实时自适应估计的算法，可以有效解决噪声特性不确定下的对准问题[2-3]，但是这类算法缺乏鲁棒性，野值会导致噪声的估计存在偏差；强跟踪算法是另一类具有代表性的自适应算法，文献[4]针对对准时出现模型失配和未知干扰时鲁棒性差的问题，引入多渐消因子，通过选取渐消因子强迫残差序列正交，从而实时调整增益矩阵，抑制滤波发散，提高算法的鲁棒性；在此基础上，郭士荦等[5]基于假设检验作为渐消因子的引入条件，进一步提升强跟踪算法的自适应性。但是强跟踪算法依赖于模型的准确性，模型的偏差会影响渐消因子的求取。因此，近年来学者们逐渐对鲁棒自适应算法展开了研究，文献[6]提出了一种基于滑动窗口的鲁棒自适应算法，通过投影统计算法先对滑动窗口内的异常新息进行降权处理，再进行自适应的估计；文献[7]进一步将遗传算法与投影统计算法相结合，实现在较强外部干扰时无人船较高精度的大失准角对准。另外，也有学者将抗差估计理论与自适应算法相结合[8]，通过协方差匹配等检测手段判别野值，对异常的新息进行降权处理，从而提高自适应算法的鲁棒性。

变分贝叶斯是近几年来新出现的近似计算贝叶斯方法中参数后验的方法，不同于以马尔可夫链·蒙特卡洛算法为代表的随机抽样算法需要通过大量重复抽样来逼近参数的真实后验，变分贝叶斯由于在具有较高估计精度的同时还有较快的计算速度，近些年来受到了广泛的关注。文献[9]在海上SINS对准中使用变分贝叶斯方法对量测噪声进行自适应估计；为了提高变分贝叶斯方法的鲁棒性，文献[10]将变分贝叶斯方法与强跟踪算法相结合，文献[11]将抗差估计与变分贝叶斯结合，抑制野值的影响。但是这些方法都没有将实际噪声的厚尾特性进行建模，无法真实反映量测噪声的统计特性。文献[12]提出在变分贝叶斯方法中使用学生t分布对厚尾噪声进行建模，但该方法假设量测噪声固定不变，具有一定的局限性。受此启发，针对恶劣海况下无人船对准时量测噪声时变且存在野值而表现出“厚尾”特性的问题，提出了一种自适应鲁棒的基于学生t分布的变分贝叶斯UKF(Student’s t Distribution Based Variational Bayesian UKF，St-VB UKF)算法，通过将量测噪声建模成学生t分布来描述存在野值时量测噪声的厚尾特性，并使用变分贝叶斯方法对其统计特性进行实时的估计。

1 SINS大失准角对准模型

无人船采用GNSS/SINS组合对准的方式。记地心惯性坐标系为i系，导航坐标系为“东北天”记作n系，实际的计算平台坐标系为n′系，载体坐标系为“右前上”记作b系。假设n系经三次转动可得n′系，三次转动角为两个坐标系间的欧拉平台误差角，记作φ＝[φxφyφz]，考虑陀螺主要误差为常值漂移误差εb和零均值高斯白噪声，加速度计主要误差为常值偏置误差∇b和零均值高斯白噪声，状态方程可由以下六个矢量方程表示:

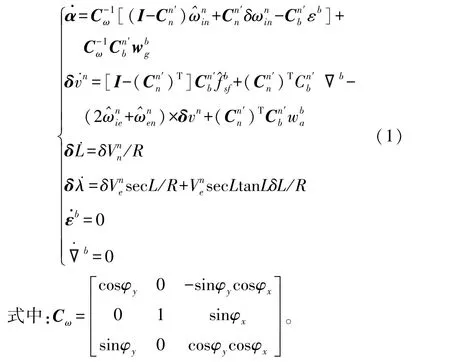
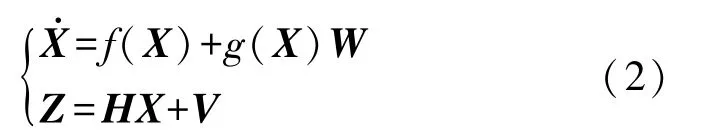
式中:H＝[I4×404×8]，f(X)和g(X)可由式(1)得到。

2 变分贝叶斯下的参数估计

2.1 变分贝叶斯原理

变分贝叶斯(Variational Bayesian，VB)方法的主要思想是通过使用形式更加简单的变分分布，将贝叶斯方法中难以直接求解的参数后验分布转换为变分分布中各个参数的优化问题。

在变分贝叶斯方法中，首先需要给待估的参数在共轭指数分布族中选取合适的先验分布。共轭性可以保证参数的先验和后验分布在形式上保持一致，从而变分贝叶斯方法在迭代更新时只需要估计各个分布中的参数而不需要直接求解后验分布就可以近似参数的后验信息。同时，在参数估计中往往需要求解多个参数的联合后验分布，为了简化计算，变分贝叶斯方法根据平均场理论(Mean Field Theory)的思想，假设所有待求取后验分布的参数都相互独立，则参数的联合后验分布可以近似成如下形式的变分分布[13]:

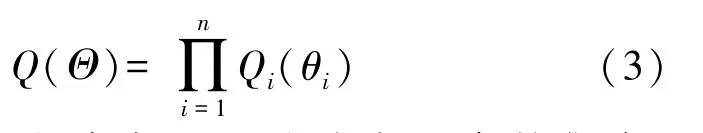
式中:Θ表示所有待求取后验分布的参数集合，Q i(θi)是每个参数在共轭指数分布族中选取的分布。

变分贝叶斯方法通过最小化两个分布间的KL散度(Kullback-Leibler Divergence)使构造的变分分布逼近真实的联合后验分布[14]:

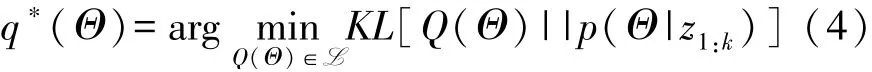
式中:z1:k表示1到k时刻的量测信息，q*(Θ)表示真实后验分布，L表示共轭指数分布族。

KL散度是一种常用的评价概率分布之间差异的度量。利用变分法来计算式(4)，则待估参数集中任意参数的后验估计可以表示为如下形式，其详细推导过程见文献[14]:

式中:φ表示参数集合Θ中的任意元素，Θ(-φ)表示除去φ的其他元素，constφ表示和φ无关的一个常量。

式(5)是变分贝叶斯方法近似计算参数后验的核心，在给待估参数集选取合适的先验分布后，通过式(5)就可以推导变分分布中各个参数的更新公式，然后利用参数的后验近似作为下一滤波时刻的先验信息，循环迭代地进行更新，从而实现自适应估计参数统计特性的目的。

2.2 厚尾量测噪声建模及参数先验分布的选取

考虑无人船在恶劣海况下对准会受到不确定的外界干扰，量测噪声具有时变特性，并且在量测中会存在部分野值，实际噪声与高斯分布相比具有厚尾特性。因此将量测噪声建模成学生t分布:

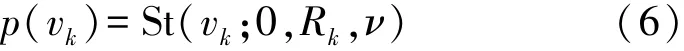
式中:St(v k；0，R k，ν)表示均值为0，尺度矩阵为R k，自由度为ν的学生t分布的概率密度函数。图1是高斯分布与学生t分布概率密度函数的对比，学生t分布在均值附近的概率更小，概率分布表现出较厚的尾部，自由度用来描述噪声的厚尾程度，自由度越小分布的厚尾程度越重。当ν→∞时，分布等价于高斯分布N(0，R k)。

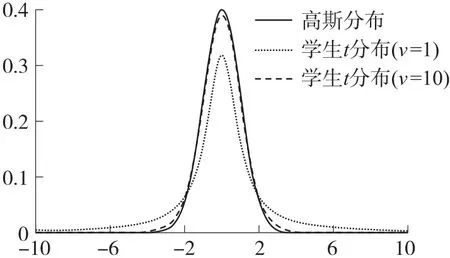
图1 高斯分布与学生t分布概率密度函数对比

由于学生t分布可以看作是高斯分布的无限混合，可以将学生t分布的概率密度写成如下形式[12]:

式中:λk是引入的辅助随机变量，学生t分布建模下量测噪声协方差阵实际为R k/λk；G(·；α，β)表示Gamma分布的概率密度函数，两个参数α，β分别表示形状参数和尺度参数，其概率密度函数形式为:

Γ(·)是Gamma函数。

为了自适应估计量测噪声的统计特性，需要给不确定或时变的参数选取先验分布，然后根据变分贝叶斯方法来计算参数的后验信息。因此，根据量测噪声的建模，从共轭指数分布族中选取Gamma分布作为辅助随机变量λk、自由度参数ν的先验分布，选取inverse Gamma分布作为尺度矩阵R k的先验分布:

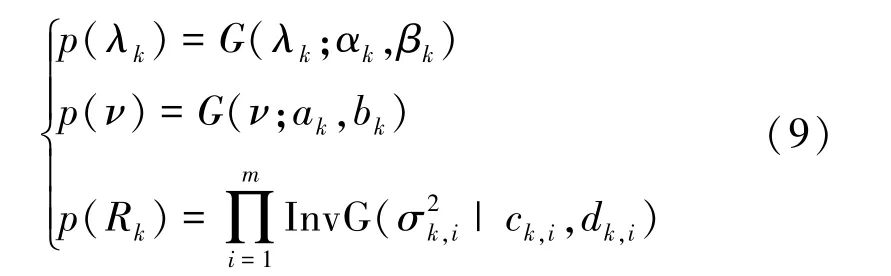
式中:InvG表示inverse Gamma分布，m表示量测向量的维数，表示量测噪声协方差阵对应对角元素的值。

同时，根据模型定义和量测噪声先验分布的选取，利用卡尔曼滤波公式可以推导出状态向量服从正态分布量测向量服从学生t分布St(z k；Hx k，R k，ν)。则根据先验分布的选取，状态变量x k、尺度矩阵R k、辅助随机变量λk、自由度参数ν和量测向量z k的联合概率密度函数为:

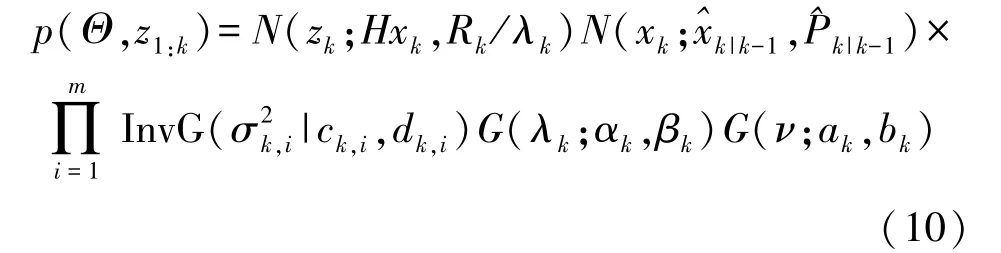
式中:待估参数集Θ＝{x k，R k，λk，ν}。

理论上贝叶斯方法的目标是根据参数先验假设和量测信息计算参数的联合后验分布，而变分贝叶斯方法将其简化成了对变分分布中参数αk，βk，a k，b k，ck，i，d k，i的迭代更新，参数的联合后验分布的计算被近似成了如下变分分布的形式:

在下一节将具体推导基于变分贝叶斯方法的参数更新以及后验近似。

2.3 基于变分贝叶斯的参数后验近似

首先，针对对准过程中噪声可能时变的情况，在计算参数后验近似之前，在先验分布的参数中引入遗忘因子ρ来加强当前时刻量测信息的权重:

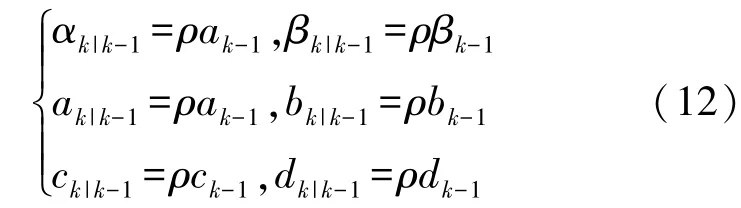
遗忘因子ρ可取(0，1]，根据文献[15]选取1-e-4。

各个参数的更新公式都是通过最小化变分分布和真实后验之间的KL散度推导得到的。将式(10)代入式(5)，取φ＝λk，可以得到:

式中:上标(i＋1)表示第i＋1轮循环变分贝叶斯方法的估计，E(i)[·]表示对应参数在第i轮变分贝叶斯迭代的数学期望，tr(·)表示矩阵的迹，由下式给出:

由于λk先验的共轭性，变分贝叶斯估计下的后验也服从Gamma分布，参数λk的后验可以表示为:

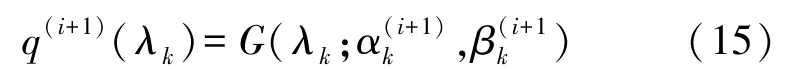
将(15)代入式(13)，可以计算参数αk，βk的更新公式为:

同理，令φ＝ν代入式(5)，得到:

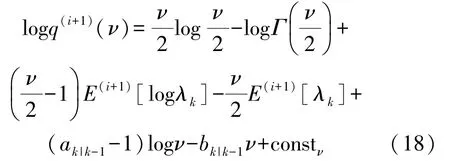
为了简化计算式(18)，基于Stirling近似，logΓ可以近似为[16]:

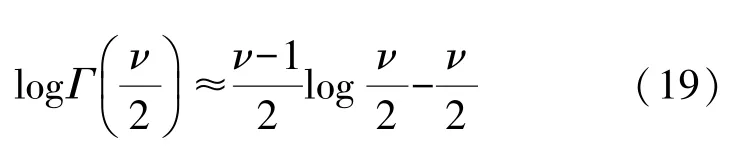
则式(18)可以简化成如下形式:

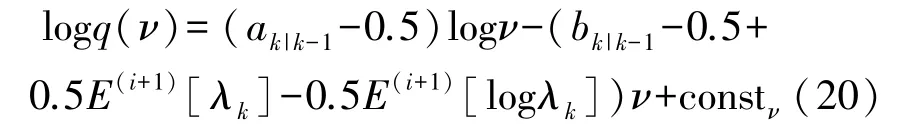
因此，自由度ν的后验可由以下公式进行更新:

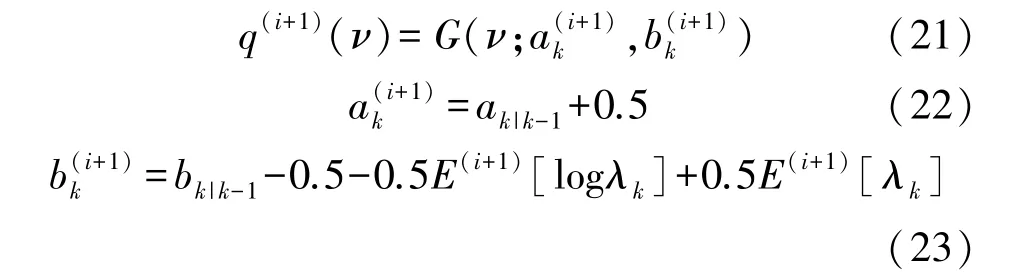
式中:根据Gamma分布的性质，有:

ψ(·)为digamma函数。

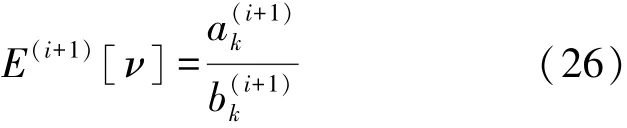
同理，令φ＝R k代入式(5)得到:

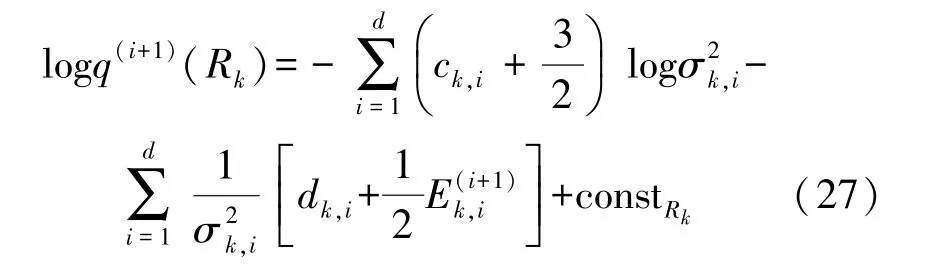
因此尺度矩阵R k的后验近似为:

其数学期望为:

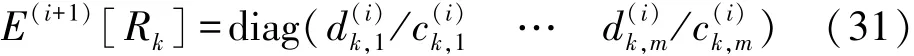
由于量测噪声建模成了学生t分布，根据式(7)，量测噪声协方差阵为尺度矩阵R k和辅助随机变量λk之商:

通过上述的公式，变分贝叶斯方法可以完成在一个滤波周期各个参数的更新，得到与先验保持一致的近似后验分布，并应用到下一滤波周期的参数估计和更新中，从而不断迭代，达到参数实时自适应估计和修正的目的。

3 基于学生t分布的变分贝叶斯UKF算法

根据第一节大失准角非线性对准模型以及第二节变分贝叶斯更新的推导，将变分贝叶斯方法与UKF非线性滤波算法相结合，设计了一种自适应鲁棒的基于学生t分布的变分贝叶斯UKF算法(简称St-VB UKF算法)，通过将量测噪声建模成学生t分布，来描述对准中存在野值时量测噪声的厚尾特性，提升算法的鲁棒性，并结合变分贝叶斯方法来实时自适应估计量测噪声的统计特性。本文提出的算法步骤概况如下:

步骤1 UKF时间更新

选取一组Sigma点来近似系统的状态变量分布，通过UT变化计算一步预测状态向量和协方差

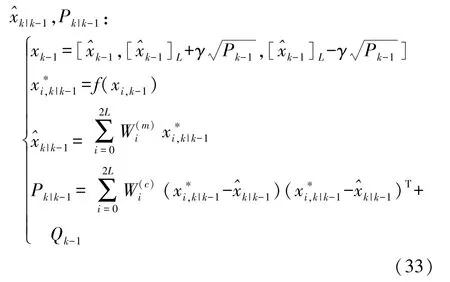
步骤2 基于变分贝叶斯的量测更新

基于变分贝叶斯方法的量测更新是通过参数的先验信息，利用量测信息来迭代更新先验分布中的各个参数，从而近似计算参数的后验，并作为下一滤波周期的先验进行循环迭代的更新。

首先根据式(12)在变分分布参数中引入衰减因子来提高当前时刻的权重，量测更新的迭代过程可以分为UKF量测更新和变分参数更新两个部分，为了提高噪声估计的准确程度，一次量测更新中可以进行N次变分贝叶斯迭代，一般进行2到3次即可。

①UKF量测更新

利用上一轮迭代的变分参数更新量测噪声协方差阵，并以此计算新一轮的卡尔曼滤波量测更新:

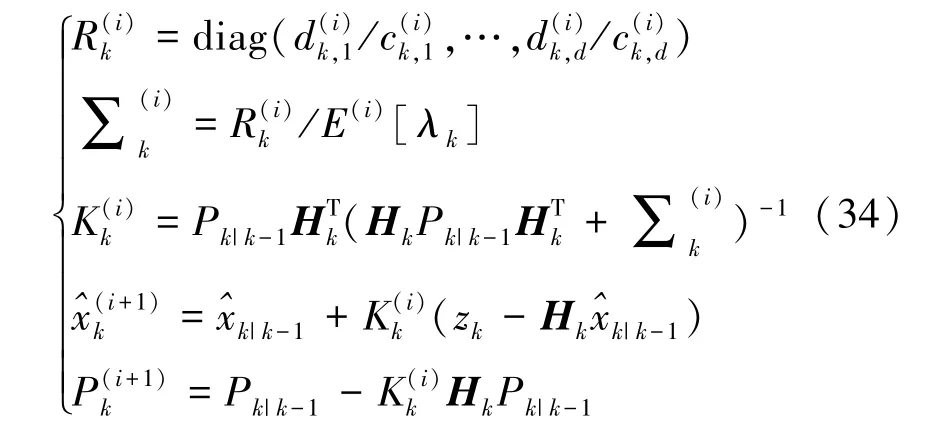
②变分参数更新

在卡尔曼滤波量测更新得到状态估计和协方差统计特性后，利用残差对变分分布中各个参数进行更新，更新的公式已经在第二章中进行了详细的推导。利用式(16)、(17)更新利用式(22)、(23)更新，利用式(29)、(30)更新；并根据其分布的特性更新辅助随机变量、自由度ν(i＋1)和尺度矩阵，进行下一轮的变分贝叶斯迭代。

N次迭代完成后，令各个参数的估计为最后一次迭代得到的结果，然后进入到下一滤波周期。整个算法的流程如图2所示。

图2 St-VB UKF算法流程图

4 仿真分析

模拟无人船在恶劣海况下的航行条件进行对准，在风浪影响下无人船受到大幅的摇摆，其航向角H、俯仰角P、横滚角R作周期变化，摇摆基座的定义如表1所示。

表1 恶劣海况下对准摇摆基座设置

其他参数设置如下:对准时的初始大失准角设置为φ＝[10° 10° 30°]，IMU参数设置为:陀螺常值漂移为0.02°/h，随机漂移为0.01°/h；加速度计常值偏置为50μg，随机偏置为10μg。仿真时间1 200 s。

同时，在实际应用中无人船在对准时可能会受到强风、浪涌等其他未知干扰的影响，且量测中会存在部分野值而使噪声表现出厚尾特性，会对对准精度和速度造成很大的影响。为了验证本文提出算法的有效性，除了表1条件下的摇摆基座外，模拟无人船恶劣海况下可能的干扰环境，在量测噪声中加入干扰噪声和野值。

仿真实验分为两个部分:①强干扰环境下的对准；②强干扰环境存在量测野值的对准。提出的算法分别与传统的UKF算法和Sage-Husa自适应UKF算法进行对比。

①强干扰环境下的对准

考虑无人船在海上对准时可能遇到强风、浪涌、冲击等未知的复杂干扰，干扰主要体现为正弦波形式的短时强干扰和瞬时的随机强干扰，因此在速度观测量中增加如表2干扰噪声。

表2 干扰环境设置

三种算法在强干扰下的失准角曲线如图3所示。取最后100 s的数据计算三个失准角的均值和标准差，结果见表3。

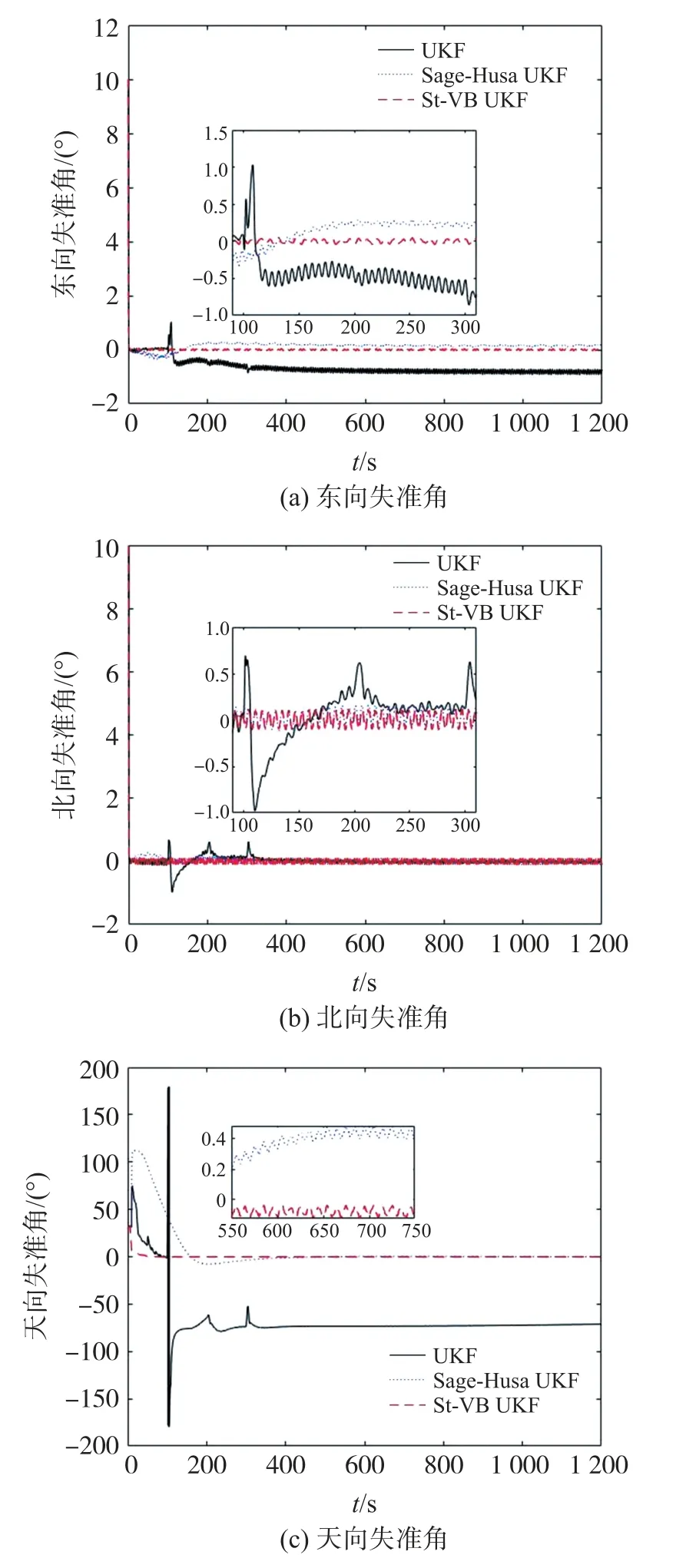
图3 强干扰下三种算法的失准角曲线

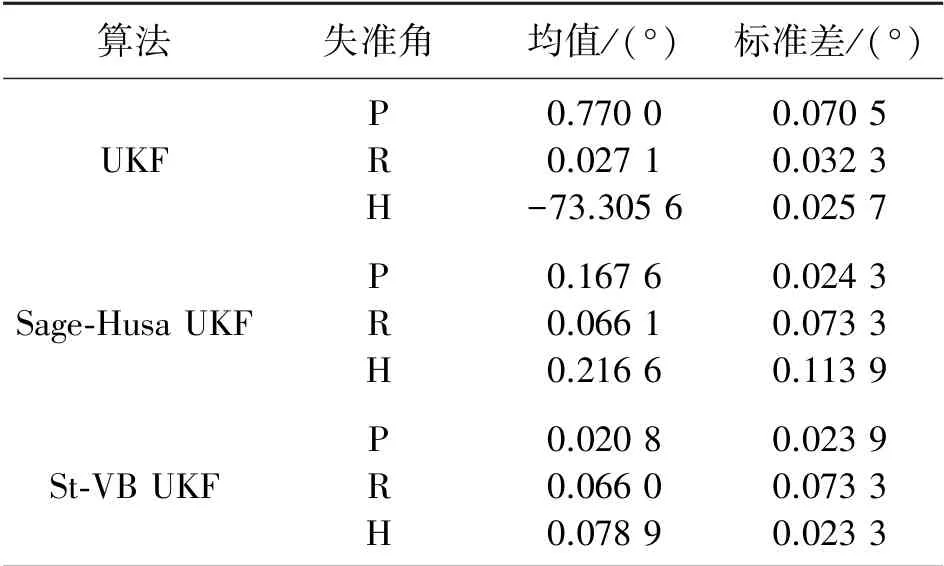
表3 强干扰下三种算法的对准结果

可以看到，在强干扰环境下，传统UKF算法在受到干扰噪声污染时失准角产生严重震荡，并导致发散。而Sage-Husa自适应UKF算法与St-VB UKF算法都可以自适应的估计和修正量测噪声的统计特性，可以抵抗干扰的影响。但是Sage-Husa算法在初期受到瞬时强干扰时出现较大误差，导致收敛速度和精度都受到影响，方位在700 s左右收敛，收敛精度水平在9′和4′左右，方位角在12′左右；St-VB UKF算法具有更快的收敛速度和鲁棒性，方位失准角在100 s左右收敛，水平方向对准精度达到1′和4′，方位对准精度在5′左右。

②强干扰环境存在量测野值的对准

实际无人船在恶劣海况下进行对准，往往由于传感器本身的误差和干扰噪声等的影响，量测输出中会存在部分野值，量测噪声具有“厚尾”特性。被野值污染的量测噪声可表示为如下伯努利分布的形式[17]:

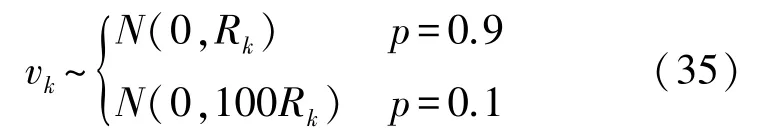
在仿真(1)的干扰环境以及式(35)描述的被野值污染的量测噪声条件下进行20次Monte Carlo仿真，三种算法的仿真结果如图4所示。

图4 强干扰环境下且存在野值时三种算法的失准角曲线

取20次仿真最后100 s的数据计算三个失准角的均值和标准差并取平均值，计算结果见表4。在强干扰且存在量测野值的情况下，传统UKF算法严重发散；Sage-Husa自适应UKF算法虽然可以自适应地修正量测噪声，但由于缺乏鲁棒性，量测在受到野值污染时对准精度下降，20次仿真平均的方位对准精度在5°左右。而本文提出的算法在自适应跟踪噪声的同时具有鲁棒性，可以抑制野值的影响，方位失准角收敛速度略慢于没有野值的情况，可以在400 s左右达到收敛，并且水平和方位的收敛精度均可达到5′以内，精度与没有野值的情况基本保持一致，具有较好的鲁棒性。

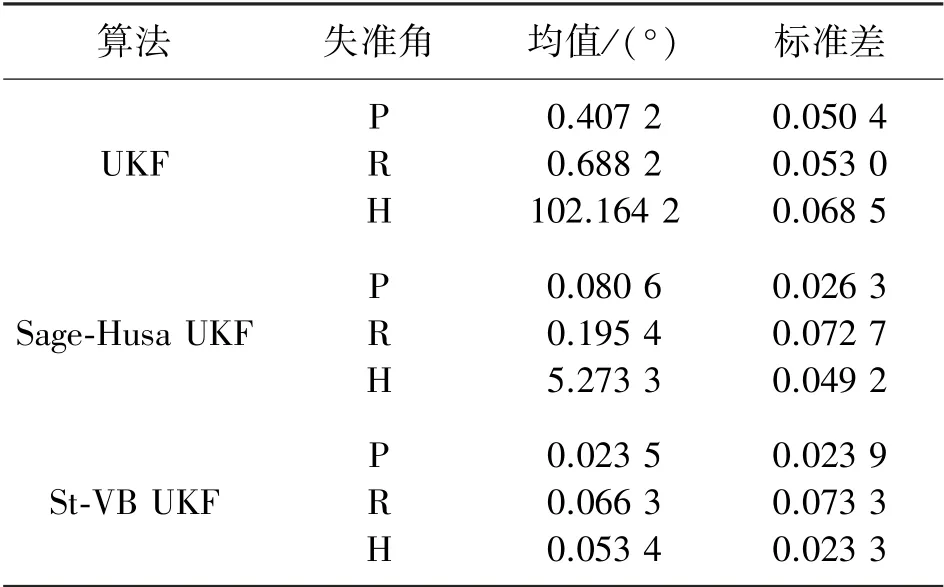
表4 强干扰下且存在野值时三种算法的对准结果

以上两组仿真结果表明，本文提出的基于学生t分布的变分贝叶斯UKF算法在短时强干扰和瞬时干扰环境下可以得到较好的对准精度，且对准速度和精度都略优于传统的Sage-Husa自适应算法；同时，当量测存在野值的条件下，提出的算法可以有效地抑制野值的影响，对准精度与无野值的情况基本保持一致，与传统算法相比具有更好的鲁棒性。

5 总结

无人船在恶劣海况下进行对准，不仅会受到大幅的摇摆，还会受到强风、浪涌等未知的复杂干扰，且由于传感器本身误差等影响，量测输出中会存在部分野值，量测噪声不符合高斯分布而具有“厚尾”特性，此时传统的UKF算法完全失效；而自适应算法虽然可以通过实时修正量测噪声的统计特性来抑制干扰噪声对对准的影响，但自适应算法缺乏鲁棒性，在野值的污染下会影响对量测噪声的估计，对准精度和速度都会受到大幅影响。

针对这一问题提出了一种自适应鲁棒的基于学生t分布的变分贝叶斯UKF算法，通过将量测噪声建模成学生t分布来抑制野值的影响，并根据变分贝叶斯方法对量测噪声统计特性和学生t分布的自由度参数进行实时的估计和修正。通过仿真实验表明，本文提出的算法在短时正弦波强干扰和瞬时随机干扰环境下对准精度略优于Sage-Husa自适应UKF算法，水平对准精度和方位对准精度都可以控制在5′以内，且收敛速度优于Sage-Husa自适应UKF算法；当存在干扰且量测噪声同时具有厚尾特性的情况下，Sage-Husa算法由于缺乏鲁棒性对准精度大幅下降，而本文提出的算法可以保证基本一致的对准精度和速度，鲁棒性更好。