压电式弹性梁生理信号传感器的建模、仿真与试验*

陈 磊王家冬查陈飞沈 驾潘文超

(浙江清华长三角研究院智能装备与技术研究中心，浙江 嘉兴 314001)

人体的生理振动信号可以反映人体在呼吸、打鼾、心跳、体动等等一系列的生理活动状态，分析其中的体征数据例如心冲击图(BCG)[1]、心率变异性(HRV)[2]、心音[3]等，可以为人体的健康状况进行评价。传统的生理信号检测方法主要是通过多导睡眠监测仪(PSG)[4]，但其需要将很多个电极直接粘贴在皮肤上，操作繁琐且影响睡眠。为了便于操作与监测，吉林大学的候天远[5]设计了一种可穿戴的生理信号监测设备，该传感器穿戴方便且无线缆约束，但使用中仍会产生异物感，且易受穿戴位置与穿戴方式的影响。此外厦门大学的张琪[6]设计了一款非接触式生理信号监测椅，非接触的设计使测试更加简便，但易受椅子本身运动的影响，且由于椅子质量与刚性较弱，所以更易受到外界的干扰。因此为了能够无接触并且稳定、长期、持续地获得人体的生理信号，根据压电效应的原理，设计了一款非接触式的压电式弹性梁生理信号传感器，通过该传感器能够对人体在床睡眠时的生理状况进行系统监测[7]。

压电式弹性梁生理信号传感器的具体使用及安装方式如图1所示，传感器固定在床板与床垫之间，靠近人体胸腔的位置。

实际的在床测试中，按照图1的方式，测试人员平躺到床垫上。与此同时佩戴多导睡眠监测仪，同时采集到心跳数据，得到的波形如图2所示。图中两张图分别为生理信号传感器数据与多导睡眠监测仪采集的数据，由图可见，传感器采集的心跳波形与多导仪的波形一一对应。

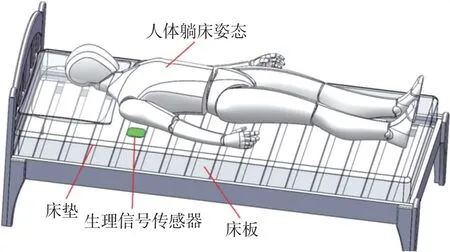
图1 生理信号传感器的安装位置

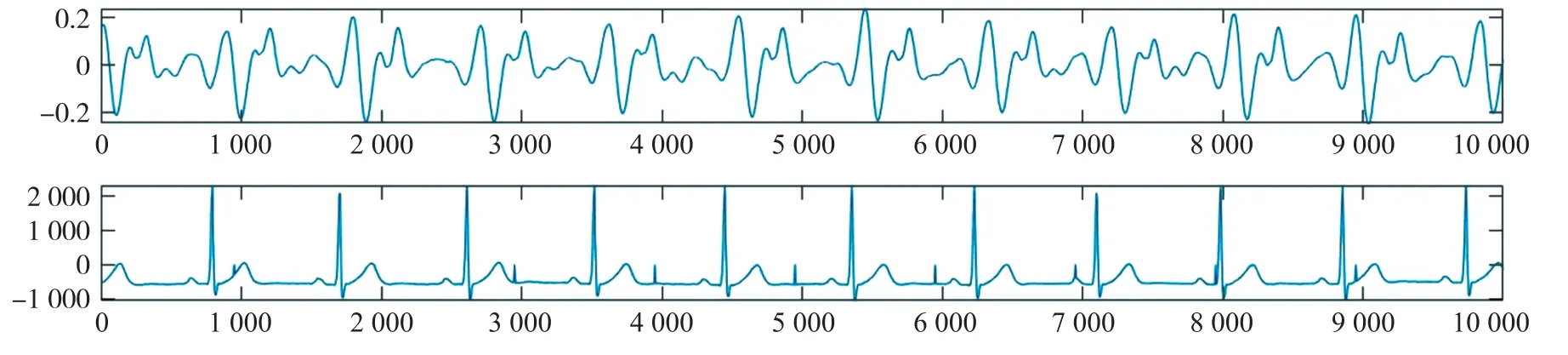
图2 传感器数据与多导睡眠监测仪数据

为了能正确地得到传感器的动态特性，避免传感器采集的信号与实际情况存在较大的偏差，结合压电效应的机电耦合理论[8]以及振动力学、材料力学的相关理论，对复杂的传感器结构进行了简化，并推导了基于压电效应的生理信号传感器的机电耦合方程，并通过与有限元仿真分析及激振器试验的对比，对理论模型进行验证。

1 传感器的机电耦合建模

基于压电效应的生理信号传感器结构如图3所示，核心结构主要包括上盖、凸点、悬臂梁、压电薄膜与硅胶垫，其中对压电薄膜的尺寸进行了放大展示。由较大表面积的上盖，对外部载荷进行广泛地接收，通过凸点将接收到的力进行集中，再将集中力作用在悬臂梁以及贴合在悬臂梁下方的压电薄膜上，悬臂梁底部是用于支撑的硅胶垫，能够减小悬臂梁的形变，避免传感器在厚度方向的尺寸过大，同时能够吸收外界的振动干扰。压电薄膜的极化方向为厚度方向，主要通过厚度方向的受力以及悬臂梁的弯曲产生电信号。

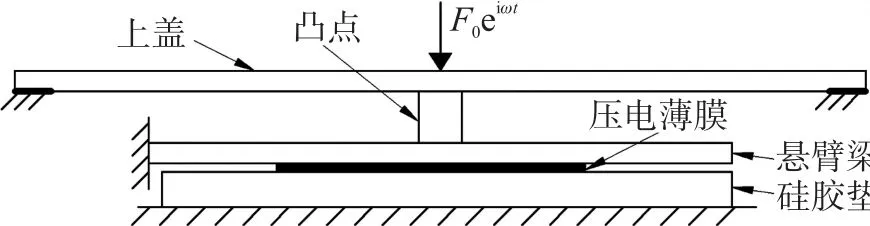
图3 基于压电效应的生理信号传感器结构图

1.1 传感器二自由度简化系统分析

整个传感器通过多个部件对力的传递产生影响，首先外载荷通过传感器的上盖与凸点传递至悬臂梁，再通过悬臂梁的弯曲变形，以及底部硅胶垫作用产生的厚度方向的变形，将力传递至贴合在悬臂梁下方的压电薄膜上，再经过压电薄膜的压电效应将产生的电荷量进行输出。根据以上的分析，首先可以将整个传感器简化为图4的一个二自由度系统[9]进行分析，两个自由度分别代表上盖、凸点的整体结构与悬臂梁这部分的结构。

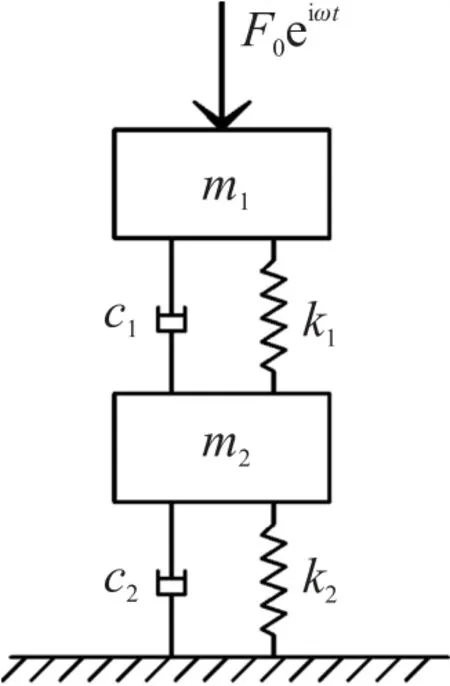
图4 传感器二自由度简化模型

因为在激振器试验中，激振器发出定频的力载荷，施加在传感器的上盖。为了与激振器试验达到一致，并进行数据对比，将简化模型中传感器所受的载荷定义为一个标准的正弦载荷。此外由于外部动载荷的激励幅值很小，对硅胶垫产生微小形变，将硅胶垫简化为弹簧与阻尼系统便于计算。

设传感器上盖表面所受的力为F0eiωt，此力通过上盖与凸点传递到悬臂梁上，传递过程中上盖与凸点的等效质量、位移、阻尼与刚度分别设为m1、x1、c1与k1；悬臂梁的质量设为m2，位移为x2。悬臂梁底部所受的阻尼与刚度分别为c2与k2。

则系统动力学方程[9]的矩阵形式为:

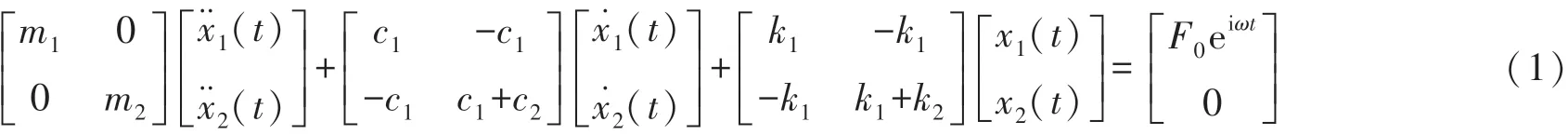
通过直接法求解式(1)，可得:

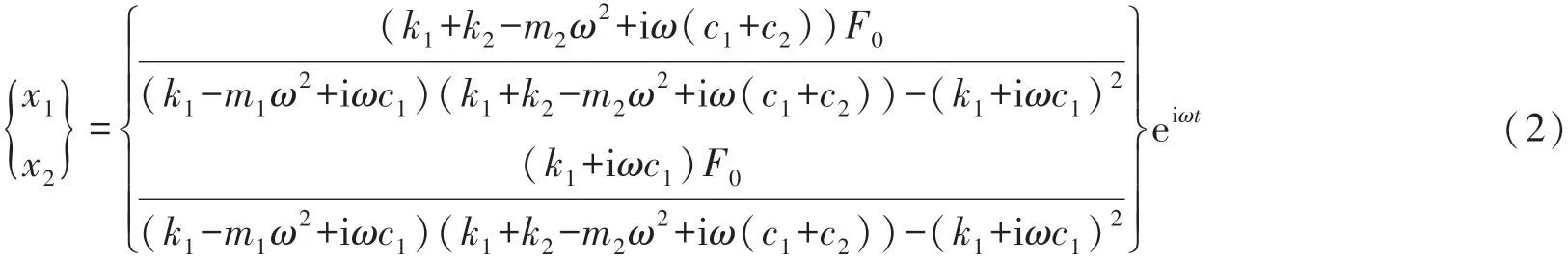
由式(2)可得悬臂梁所受的载荷表达式为:

1.2 传感器欧拉-伯努利梁简化分析

根据求得的悬臂梁上的受力情况表达式(3)，以悬臂梁作为分析对象，考虑其弯曲变形进行建模分析。根据悬臂梁的实际尺寸，其厚度与长度的比值很小，约为0.02，是明显的细长梁，且主要外界振动为低频振动，可以忽略剪切变形以及截面绕中性轴转动惯量的影响，所以将其简化为欧拉-伯努利梁[10]，简化模型如图5所示。

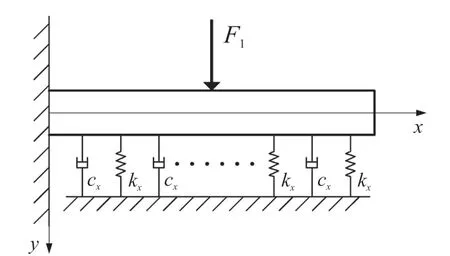
图5 传感器欧拉-伯努利梁简化模型

悬臂梁左端固定，右端自由，悬臂梁上表面的中间受到F1的载荷作用，底部受到均布的阻尼与刚度支撑，并建立图中坐标系。

则梁上的微段dx的受力情况[10]如图6所示。

图6 d x长度悬臂梁微段的受力分析

其中ρ为悬臂梁的体密度；S为悬臂梁的截面积；c x为悬臂梁底部单位长度上的阻尼，其中cx＝c2/l；k x为悬臂梁底部单位长度上的刚度，其中k x＝k2/l；fdx为微元所受的载荷。

由力平衡方程[10]有:

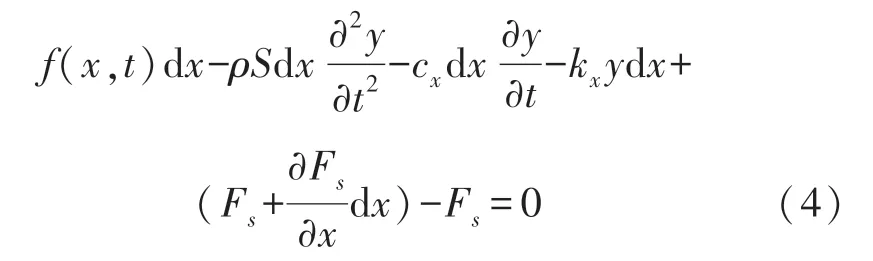
由力矩平衡方程[10]有:

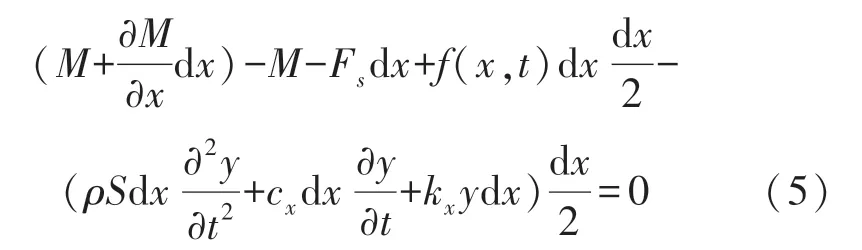
式(5)忽略高阶小量得:

根据弯矩与挠度的关系[11]:

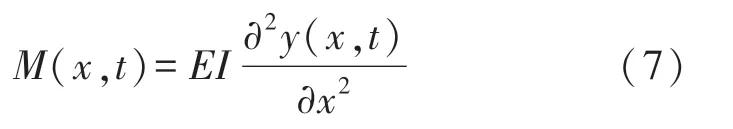
式中:E为弹性模量，I为截面对中性轴的惯性矩。

将式(6)与式(7)代入式(4)，得到等截面梁的动力学方程为:

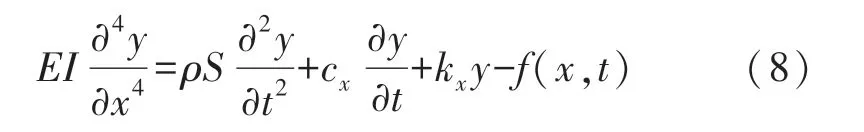
由于悬臂梁上的凸点相对于悬臂梁整个长度较小，所以将施加在悬臂梁上的力设为集中载荷，施加于悬臂梁中部，即

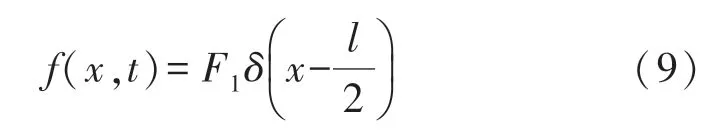
设梁的稳态响应为:

将式(9)与式(10)代入式(8)，通过拉式变换与反变换，得到方程的通解为:

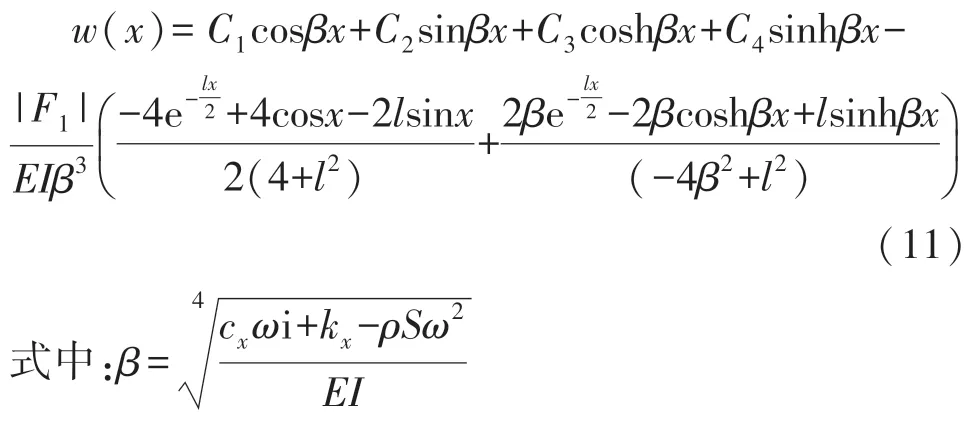
根据梁的边界条件[10]:

固定端:y(0，t)＝0，y′(0，t)＝0

自由端:EIy″(l，t)＝0，[EIy″(l，t)]′＝0

代入到式(11)中，可求得C1、C2、C3、C4参数，由此可得悬臂梁中性轴的稳态响应y(x，t)。

1.3 传感器机电耦合分析

由于压电薄膜厚度只有悬臂梁厚度的百分之五，所以忽略其厚度对悬臂梁中性轴产生的影响，仍以悬臂梁中性轴进行计算，得到压电薄膜在x轴方向的应变[12]为:

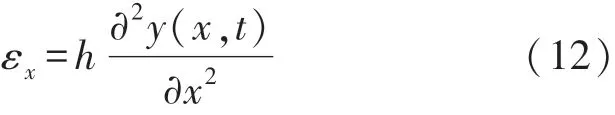
式中:h为压电薄膜到悬臂梁中性轴的距离。

由此可得压电薄膜在x轴方向所受的应力为:

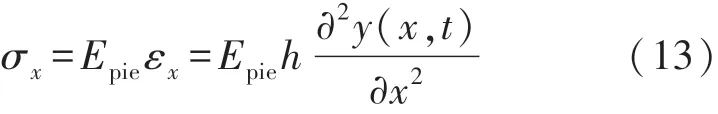
式中:Epie为压电薄膜的弹性模量。

同时可得压电薄膜在y轴方向所受的应力为:

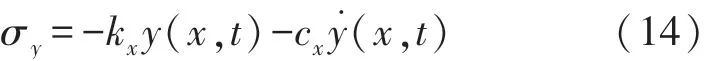
由于在求得x轴方向的应力时引入了y方向压电薄膜到悬臂梁中性轴的距离h，导致该应力所对应的微元与求得y轴方向应力所对应的微元不一致，为了将两者统一，将x轴的应力进行如下的转换:

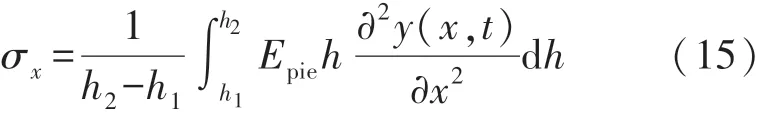
式中:h1和h2分别为压电薄膜在y轴方向上下表面到悬臂梁中性轴的距离。

根据压电方程D＝dT＋εTE[13]，其中T代表应力张量，E代表电场，D代表电位移场。材料参数d和εT分别代表材料的耦合属性和在恒定应力下的介电常数。并且由于没有外加电场，以及忽略二次压电效应，可以得到压电薄膜在y轴方向上产生的电位移为:

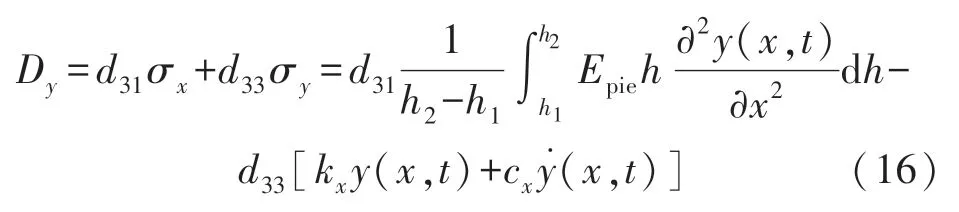
式中:d31和d33分别为压电常数。

由此可得压电薄在上表面产生的电荷量为:

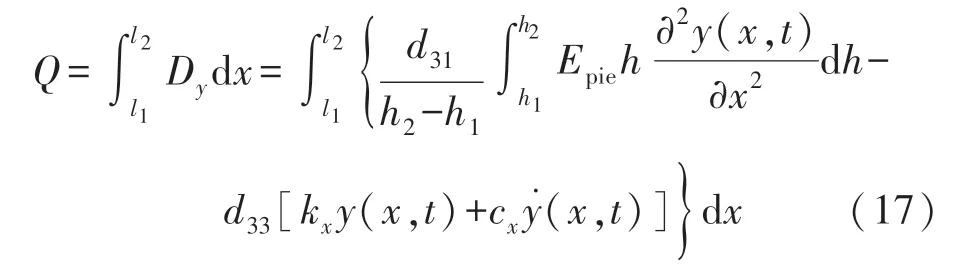
式中:l1和l2分别为压电薄膜x轴方向两端的坐标位置。

2 传感器有限元仿真

传感器的有限元仿真通过COMSOL软件实现，由于传感器是对称结构，并且所受的载荷与约束也是对称的，所以仿真中沿对称面建立二分之一的结构模型，对称面上的法向位移设置为0。在传感器底面设置为固定约束，对螺栓螺纹的连接设置为5 N预紧力，在上盖施加0.05 N的正弦载荷。在传感器内部的结构之间，设置硅胶垫与压电薄膜之间、硅胶垫与悬臂梁之间以及上盖与凸点之间为接触设置，其他连接部分如上盖与传感器壳体之间、螺栓与悬臂梁所在的PCB板之间、PCB板与壳体之间、凸点与悬臂梁之间的边界设置为连续性边界，由此建立图7所示的有限元仿真模型。

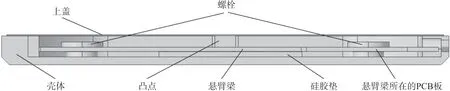
图7 传感器仿真模型

对有限元模型的材料进行设置，将上盖、凸点及螺栓的材料设为结构钢，壳体的材料设为ABS，PCB板设为FR4，压电薄膜设为聚偏氟乙烯[14](PVDF)材质，硅胶垫的本构模型选择Mooney-Rivlin双参数模型[15]，并对结构设置相应的瑞利阻尼。在静电接口中，设置压电薄膜下表面电极接地。压电薄膜、悬臂梁及硅胶垫的几何和材料参数如表1所示。

表1 压电薄膜、悬臂梁及硅胶垫几何和材料参数

仿真得到压电薄膜与硅胶垫在1 Hz频率时所受的应力与变形情况，如图8与图9所示。

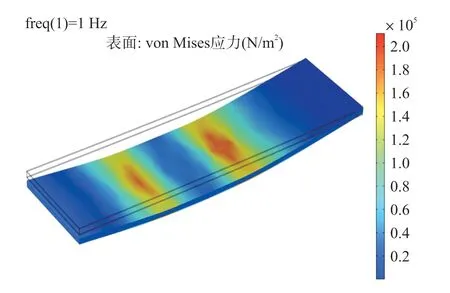
图8 压电薄膜所受应力与变形情况

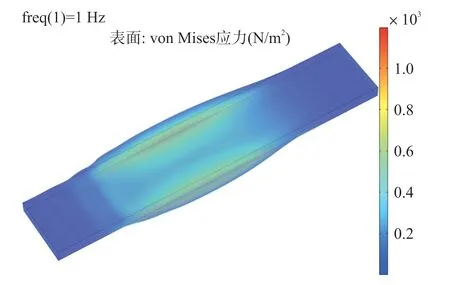
图9 硅胶垫所受应力与变形情况

通过频率扫描最终得到在0.027 N与0.2 N载荷下，压电薄膜产生的电荷量幅频曲线如图10所示。0.027 N与0.2 N为标准力传感器采用相同的外壳安装在床时，采用厚薄两种床垫，通过人躺床测试得到的心跳力值的峰值。仿真结果显示，在不同载荷下，幅频曲线的趋势一致，且由于受到结构阻尼的影响，传感器产生的电荷量在高频阶段发生了很大的衰减，在载荷频率大于20 Hz之后，传感器输出电荷量幅值逐渐保持稳定。

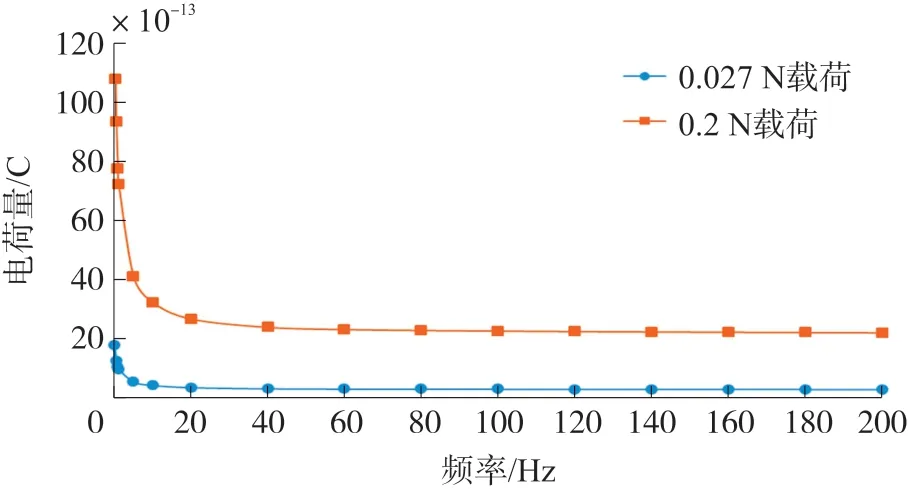
图10 仿真得到的传感器幅频响应曲线

3 激振器试验验证

为了对传感器的动态特性进行测试与验证，采用稳态正弦激励的方式，激励源使用The Modal Shop公司的电动激振器2025E以及2100E21-400型功率放大器。通过激振器对传感器上盖施加一个频率和大小都可调节，且具有单一频率的简谐激振力，依据传感器输出的信号，通过换算可以得到传感器产生电荷量的幅频响应曲线。

激振器试验设备的原理结构如图11所示，主要结构包括激振器、激振器升降机构、传感器治具、标准力传感器、压力传感器等。激振器试验设备实物结构如图12所示。

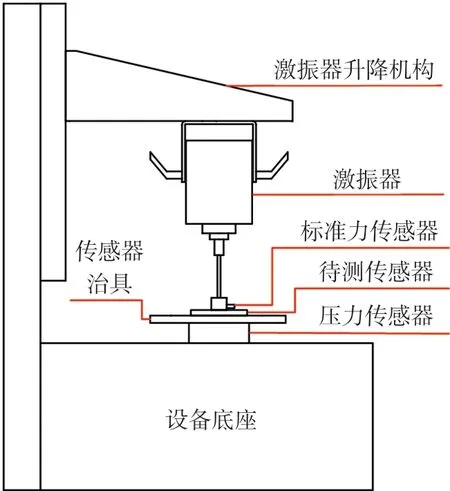
图11 激振器设备原理图

图12 激振器试验设备

激振器发出正弦激励，通过激振器推杆以及中间传递过程，传递至被测传感器上方的力传感器上，由力传感器输出的信号作为反馈，对激振器电压进行调节，使最终传递至被测传感器上的力的幅值与频率都稳定且准确。

由于人体产生的生理信号主要频率在50 Hz以内，所以激振器对该生理信号传感器的频率检测范围主要在200 Hz以内。试验中采用激振器对多个频率进行定频激励，通过被测传感器上盖上方的力传感器反馈的载荷值，自动调节功率放大器的输入电压，使不同频率下载荷的大小一致且稳定。通过激振器分别施加0.027 N与0.2 N的载荷力，得到传感器的幅频响应曲线如图13所示。电荷量幅值同样在高频阶段发生了很大的衰减，在载荷频率大于20 Hz之后，传感器输出电荷量幅值逐渐保持稳定。

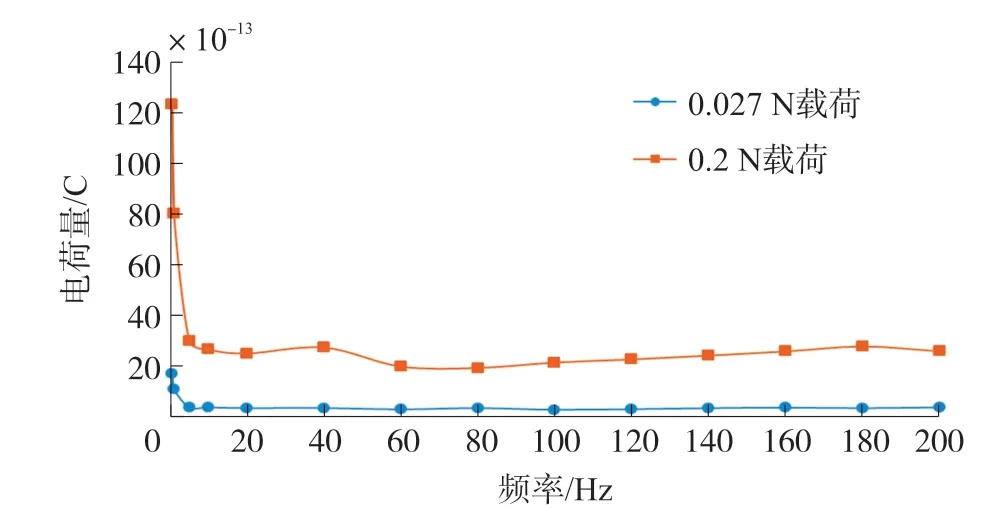
图13 激振器试验得到的传感器幅频响应曲线

4 结果对比分析

根据机电耦合模型所得到的方程(17)，代入相关的几何与材料等参数，可以得到理论计算的幅频曲线。对比图10仿真的数据与图13激振器试验的数据，可以得到0.027 N与0.2 N载荷下传感器幅频曲线分别如图14与图15所示。

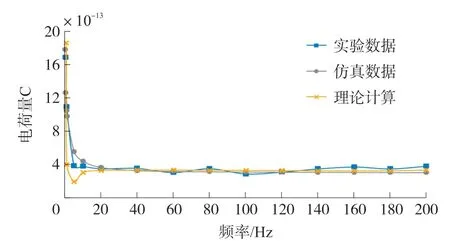
图14 0.027 N载荷下传感器幅频曲线

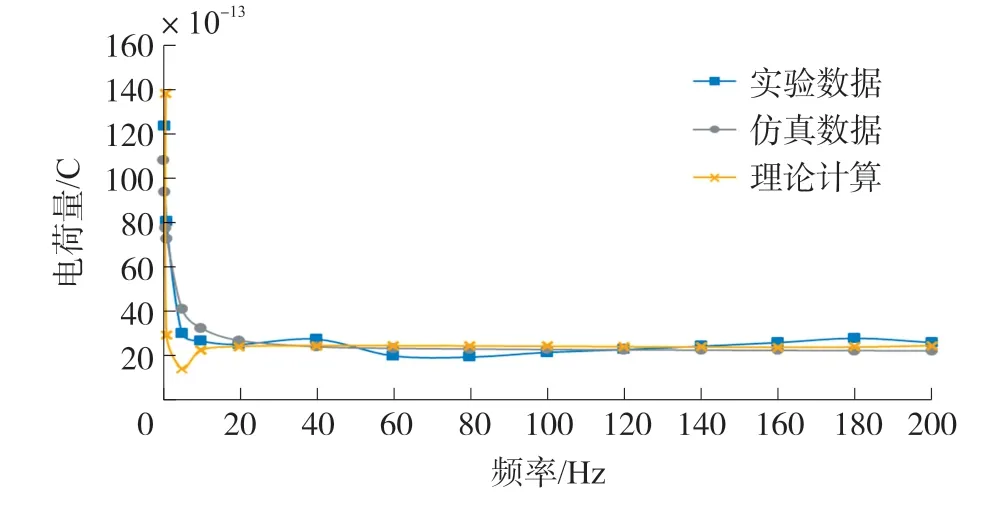
图15 0.2 N载荷下传感器幅频曲线

根据图14与图15可以看出，在不同载荷下，传感器的幅频曲线趋势都较为一致，都是在低频时幅值较大，随着频率的增加，幅值在0～10 Hz产生了很大的衰减，到20 Hz以后保持幅值的稳定，波动较小。试验、仿真与理论数据三者之间，幅频曲线的趋势都保持一致，但是在频率低于20 Hz时，幅值在数值上差别较大，主要原因是受阻尼参数以及激振器试验中附加元器件的影响较大。在频率20 Hz以上，三者的数据都能达到稳定的状态，且三者的数值偏差平均在2.5%以内，三者的幅值吻合得较好。

5 结论

本文通过理论分析，对压电式弹性梁生理信号传感器建立简化模型，并得到其产生电荷量随施加载荷变化的方程；利用COMSOL软件对传感器模型进行仿真计算；通过激振器试验平台，对该传感器的动态特性进行试验研究。综合理论分析、仿真计算与试验研究结果，可以发现，该传感器在频率20 Hz以上时幅值能够保持稳定，同时理论模型、仿真及试验的结果都较为吻合，可以验证理论模型及仿真计算的正确性。为进一步提高传感器性能提供了理论依据与仿真计算的验证模型，对今后批量化的生产及检测提供了试验平台与帮助。