光滑度量测度空间上熵沿几何热流的演化公式

毛晶晶

(江苏省南通卫生高等职业技术学校 基础部，江苏 南通 226000)

0 引言

设(M,g,dμ)为光滑度量测度空间, 其中M为n维闭的黎曼流形, dμ=e-f(x)dx是关于某个给定势函数f的加权测度。 当考虑光滑度量测度空间上的问题时我们常用Bakry-Emery曲率

来替代Ricci曲率, 其中m>n。 加权Laplacian定义为Δf=Δ-▽f·▽。容易看出Δf关于加权测度dμ是对称的。

本文在度量沿着一类几何热流演化的闭光滑度量测度空间上引入新的加权Shannon和Fisher熵, 并推导出这两种熵的演化方程以及单调性。 作为应用, 建立了相应的渐进估计。

1 相关定义

我们假设度量(gt)t≥0满足如下的演化方程

∂tg=h

(1)

在文献[1]中加权Shannon熵定义为

(2)

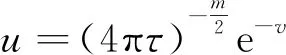
加权Fisher 熵定义为

则加权Perelman熵可以定义

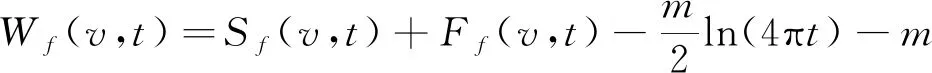
(3)

容易看出

Wf(g,u,t)

如下的加权Bochner公式很有用[1-4]

(4)

2 演化公式

文献[5]中证明了熵W0(v,t)沿着Ricci流

∂tg=-2Ric

和共轭热方程耦合系统的单调不增性。这一节我们来建立加权Shannon熵和Fisher 熵沿着更为一般的几何热流 (1) 的演化公式。 为此，设f为方程

(5)

的解。由[6]知Rimann-Lebesgue度量dx满足

则有

∂t(dμ)=0

设u是方程

(Δf-∂t)u=0

(6)

的正解。则有

因此我们设

(7)

由(2)知

(8)

注意到

因此

利用加权Bochner公式 (4),类似于 [7] 中的计算, 易得

因此

(9)

由 (8) 可得

结合(3)可得

(10)

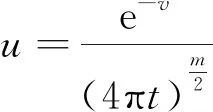
(11)

证明由 (8), (9) 和 (10)，可得

因此 (11) 成立。

3 单调性和渐进性

定理2 在定理1中特别地取f为方程

(12)

的解。度量(gt)t≥0满足加权Ricci流

∂tg=-2Ricf,m

(13)

那么Wf(g,u,t)沿着方程(6)单调不增。

证明此时 (11) 可以变形为

因此Wf(g,u,t)单调不增。证毕。

当t→∞，我们得到了Sf(g,u,t)和Wf(g,u,t)的渐近估计。

定理3 设M为n维闭的黎曼流形，度量(gt)t≥0满足加权Ricci流 (13)，f为方程 (12) 的解，则沿着加权热方程 (6)，

(14)

且

(15)

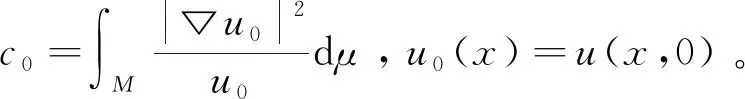
证明由 (9) 可得

注意到

为了叙述方便，记

由Hölder不等式可得

=(-c+A)2

另一方面，

计算可以得到

因此，得(14)和(15)。