计及暂态模式切换下垂控制逆变器故障下同步稳定分析

马堰泓，付立军，胡祺，王光宇，刘陈瑞扬

(海军工程大学 舰船综合电力技术国防科技重点实验室，湖北 武汉 430033)

0 引 言

近年来，风力发电、光伏发电等可再生能源发电技术得到了快速发展，分布式电源大规模接入，使得现代电力系统中传统的同步发电机所占比例不断降低，非同步机电源所占比例则逐步增加，而大多数非同步机电源均通过逆变器接口接入大电网[1]。

逆变器的控制方式可分为多种，例如虚拟同步机控制[2]、基于锁相环的控制方式[3]和下垂控制等。相比其他控制方式而言，下垂控制具有结构简单、安装维修便捷、易于控制、系统扩容方便、成本低等优势[4-5]。

对于并网或孤岛运行的下垂控制逆变器，频率同步是维持有功功率稳定的必要条件。与传统同步电机具有旋转质量块不同[6]，下垂控制的逆变器属于静态功率变换装置，不存在同步电机的“功角”摇摆过程[7-8]，应把经典定义中表征电机受到扰动后与电网保持同步能力的暂态稳定性扩展为同步稳定性[9-11]，依据扰动大小可分为小扰动(静态)与大扰动(暂态)两类[12]。

其中，小扰动下的稳定性可在时域或复频域线性化分析，已初步形成理论体系[13]；而大扰动同步稳定性只能通过时域分析，无法对扰动前平衡点进行线性化处理，分析方法更加复杂，是目前学术研究的热点。对此，文献[14]针对大扰动对交流微电网安全运行产生影响的问题，分别从微电网电流特性与稳定运行特性两个角度进行了分析，但仅仅只是对国内外研究基础的概括与总结，并没有提出具体的控制策略；文献[15]指出，由于电力电子设备的弱应力承受性，在大扰动下逆变器存在因电流过大被烧毁的风险，但并没有对如何限制过电流进行深入分析；文献[16]通过在下垂控制的逆变器系统中添加电流限制，使得大扰动下逆变器的输出电流饱和，逆变电源由电压源切换为电流源，但并没有对暂态切换过程进行深入分析。因此，含有电流限幅的逆变器同步稳定性分析方法有待提出。

能量函数法是评估电力系统暂态稳定性最常用的方法之一，而Lyapunov暂态能量函数法能快速分析微电网系统在预想大扰动下的暂态稳定度[17]。目前，基于Lyapunov能量函数的方法，如波波夫绝对稳定性准则[18]、散耗系统理论[19]、基于T-S模糊模型的方法[20]等等，均已被用于评估逆变器的同步稳定性。文献[21]利用Lyapunov直接法构建了单相逆变器的能量函数，但该方法存在一定的局限性，并未考虑电流限幅对逆变器同步稳定性的影响。

为此，文章对基于下垂控制的逆变电源开展研究。首先建立下垂控制逆变器同步动态动力学模型，分析以电网电压骤降为例的电网故障下，电压源/电流源暂态模式切换对等效功角曲线的影响；然后利用Lyapunov直接法分析电压骤降对系统吸引域的影响，并通过等面积法分析在电流饱和与不饱和情况下系统的同步稳定性，仿真验证分析的正确性；最后，提出一种基于切换有功与无功控制方式的优化控制策略，理论分析该策略的可行性，仿真验证该策略的有效性。

1 系统结构

下垂控制的基本控制原理主要是通过模拟同步发电机的频率和电压调节特性，从而达到对微电源更加方便有效的控制，实现有功功率和无功功率在并联逆变器之间的平均分配。

基于下垂控制的三相电压源型逆变器的拓扑图如图1所示。逆变器采用旋转坐标系下的矢量控制，控制结构可分为三层。最外层为有功调频、无功调压下垂控制，有功调频下垂控制通过结合输出有功功率及额定角频率得出角频率参考值，无功调压下垂控制通过结合输出无功功率及额定电压得到电压参考值，用于多逆变器间并联功率均分。中层的dq轴电压控制用以调节输出电压跟随指令值，其检测dq轴电压反馈与指令值的偏差，通过PI控制器调节输出电流指令，驱动电压反馈跟随电压指令，防止过流，往往加限幅值。内层的dq轴电流控制用以调节输出电流跟随指令值，其检测dq轴电流反馈与指令值的偏差，通过PI控制器调节输出电压，驱动电流反馈跟随电流指令，并产生电压调制波，通过PWM模块以驱动半导体开关。

值得注意的是该级联控制结构下，为保证逆变器动态响应特性与稳定性，功率下垂环、电压环、电流环三环控制的响应时间有所不同，一般情况下电流环控制的响应速度快于电压环控制，而由于在功率下垂环控制中往往会添加低通滤波，所以功率控制环响应速度最慢，时间最长。针对系统同步稳定问题，主要与下垂控制相关，因此可重点关注下垂控制动态影响，电压环与电流环的响应时间可暂时忽略不计。

由于逆变器的弱应力承受性，为保证故障等大扰动下不过流，电流指令往往进行饱和限幅设计，使得限幅前dq电流指令由dq电压控制调节，限幅后dq电流指令由限幅值决定。下垂控制逆变器常采用基于d轴优先的电流参考限制策略，这种策略描述为：

(1)

(2)

根据式(1)，将电流饱和模式定义为逆变器输出电流幅值达到Imax并受电流限制策略限制的场景，而电流不饱和模式定义为逆变器输出电流幅值小于Imax的场景。

综上所述，由于电流指令饱和限幅，下垂控制逆变器存在电压源/电流源暂态模式切换过程。系统正常工作时，逆变电源可等效为串联输出阻抗的受控电压源。由于逆变器承受过压过流能力较弱，故障下逆变器可能会进入电流饱和模式，这使得电流环失去控制，导致逆变电源由电压源切换为电流源，如图2所示。这种电压源/电流源暂态模式切换的情况，导致逆变电源的同步稳定问题分析复杂。

2 同步稳定性分析模型

下垂控制逆变器采用有功调频、无功调压下垂控制策略，即：

(3)

其中：V0为无功-电压下垂控制的电压给定值；Pref和Qref分别为逆变器的有功功率与无功功率的给定值；PE和QE分别为逆变器的输出有功功率和无功功率；Kp和Kq分别为有功-频率和无功-电压下垂控制系数；ω为逆变器的角频率参考值；ω0为无穷大电网的角频率、即额定角频率。

为滤除高频扰动，通常对功率检测值进行低通滤波，表达式为

(4)

其中：滤波后逆变器的输出有功功率为Pf；T为低通滤波时间常数。

结合式(3)和式(4)，有功调频下垂控制动态可表示为

(5)

基于式(5)可得

(6)

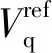
(7)

其中：XΣ表示LCL滤波器电网侧阻抗与线路阻抗之和；U表示电网电压的大小；V表示逆变器输出电压的大小。

故障下，逆变器输出电流变为饱和，逆变电源由电压源切换为电流源，基于d轴优先级的电流参考限制策略，当逆变电源切换为电流源后，电流幅值由限幅值决定，相位定位于d轴。暂态饱和切换的向量图如图3所示。

因此，电流饱和时逆变器有功功率PE可计算为

PE=ImaxUcosδ=Psmcosδ。

(8)

其中：Imax表示电流限幅值；U表示电网电压的大小。根据式(5)、式(7)和式(8)可绘制出下垂控制的逆变器中有功-频率控制的动态响应，如图4所示。

3 同步稳定机理研究

3.1 基于Lyapunov直接法构造能量函数

根据图4可以得到下垂控制的逆变器系统在电流不饱情况下的状态方程为

(9)

结合式(9)和式(6)可得

(10)

基于式(7)，通过将PE赋为Pref可得逆变器在故障前的稳定平衡点δs表达式为

(11)

为了采用Lyapunov直接法构造能量函数，需要将稳定平衡点从(δs，ω0)平移到(0，0)，定义：

(12)

因此，状态方程(10)可以写作：

(13)

对其构造Lyapunov能量函数为

(14)

在电网电压骤降这类电网故障情况出现后，由于逆变电源存在从电压源切换为电流源、电流非饱和切换为饱和的过程，因此不同时刻的稳定平衡点δs、不稳定平衡点δu也将发生改变。平衡点的改变过程将在3.2节具体分析。

从数学角度讲，构造Lyapunov能量函数的目的在于研究在故障清除时系统的状态变量是否在吸引域内，从而判断系统能否回到稳定状态。因此需要计算不同时刻的临界能量。临界能量Vcr定义为系统处于不稳定平衡点时，以稳定平衡点δs为参考点系统所具有的势能。

首先通过系统功角特性曲线得到故障发生后系统的稳定平衡点与不稳定平衡点，分别用(δs，ω0)和(δu，ω0)表示，然后将不稳定平衡点(δu，ω0)代入式(14)即可计算出临界能量Vcr。根据上述步骤，可以得到临界能量函数表达式为

Vcr=V(δu,ωg)。

(15)

故障发生后，通过计算故障清除时系统的角频率ωc与功角δc，将其带入式(14)中可以得到故障后系统的总能量Vc。当Vc

考虑到电压源/电流源暂态模式切换过程，在故障发生时，逆变器输出有功功率表达式由式(7)切换为式(8)，能量函数表达式(14)将会变为

ImaxU(sin(x1+δs)-sinδs)+

(16)

3.2 系统同步稳定分析

在3.1节的分析中，逆变器功角变化率与输出有功功率之间的关系式如式(10)所示。直接绘制系统功角特性曲线，利用能量函数法来对系统的稳定性进行分析。

由式(7)和式(8)绘制出下垂控制逆变器在电流饱和与非饱和情况下的功角特性曲线，如图5所示。

结合所建模型以及动力学方程(10)可知，逆变器的输出有功功率PE与功率给定值Pref的偏差可以驱动逆变器角频率的加速或减速。因此，在功率给定值Pref下方的区域可定义为加速区域，功率给定值Pref上方的区域可定义为减速区域。如果系统工作点在经过加速区域和减速区域后没有出现不稳定性，那么系统就会稳定在一个平衡点，这个平衡点就是功角特性曲线与功率给定值的交点。

由图5可知，电网电压U跌落程度决定了故障后的饱和功角特性曲线是否与功率给定值Pref相交。因此可定义中度电网电压跌落的情况为：饱和功角特性曲线与功率给定值存在交点；重度跌落的情况则没有交点。可描述为：

(17)

下文将分两种情况对电网故障时逆变器的同步稳定性进行分析。

3.2.1 重度电网故障的情况

在重度电网故障的情况下，电网电压幅值从U突降为U′时，逆变器的功角特性曲线如图6所示。其中，P(1)与P(2)分别为电压骤降前后饱和功角特性曲线。当功率给定为Pref，且系统处于稳态时，工作点稳定在A点。

当电压骤降发生时，逆变器进入电流饱和模式，工作点从A点突变至A′点。A′点的输出有功功率PE小于Pref，此时系统进入加速区域，逆变器功角沿着饱和功角特性曲线P(2)持续增大。由图6可知，故障期间系统不存在平衡点，因此也就无法达到平衡状态。

设E′点为故障恢复点，故障恢复后，工作点由E′点突变至E点，故障恢复时的功角特性曲线如图7所示。

故障切除过程中，系统的加速面积是S1，减速面积是S2。加减速面积的表达式如下：

(18)

假设在F点切除故障时，加减速面积相等，即S1=S2，称F点为临界清除点。通过临界清除点可将故障切除分为3种不同的情况，如图7所示，下文将分别进行分析。

1)当δE≤δF时，故障切除后逆变器的输出有功功率PE>Pref，系统进入减速区域，逆变器的功角沿着饱和功角特性曲线P(1)减小。

此时系统的加速面积S1小于减速面积S2，由等面积法则可知，系统最终将会稳定在A点。

2)当δF<δE≤δD时，故障切除后逆变器输出有功功率PE仍然大于功率给定值Pref。但由于δE>δF，导致系统的加速面积S1大于减速面积S2，因此系统不会稳定在A点。逆变器的功角会沿着饱和功角特性曲线P(1)持续减小，最终稳定工作在C点。值得注意的是，C点不是理想的工作点，因为C点处电流仍然饱和，电压仍然不受控制，在工程实践中要尽可能避免。

上述两种情况，由于切除时间的不同，导致故障切除时系统的能量发生变化，使得系统稳定平衡点由A点切换到C点。

根据Lyapunov能量函数(14)可计算出该过程的吸引域的变化情况，如图8所示。其中，Vcr1和Vcr2分别表示故障修复后回到平衡点A点和C点吸引域的临界能量。由图可知，故障切除时系统运行点回到稳定平衡点A点要比回到C点更加困难。

图9用Lyapunov直接法展示了故障切除时系统能量与临界能量的对比。临界能量Vcr1和Vcr2与图8中的曲线一致。由图9可知，故障发生后，系统总能量随时间增加。当能量超过Vcr1后，系统的稳定平衡点由A点切换到C点。若故障清除时系统的总能量低于临界能量，则系统能保持同步稳定。反之，若故障切除时系统的能量超过了临界能量，则无法保持稳定。

根据表1的数据构建仿真模型，首先计算临界清除角δF。由式(18)可得，当S1=S2时，δF=0.69 rad。

仿真结果如图10所示，其中Tc表示从故障切除时间。根据仿真结果可知，当Tc=0.48 s时，对应逆变器的功角δ=0.681 rad，满足δE<δF条件，系统能够回到稳定平衡点A点。当Tc=0.49 s时，逆变器的功角δ=0.698 rad，满足δE>δF，加速面积大于减速面积，系统的工作点最终稳定在C点。因此，仿真结果与理论分析一致，证明了同步稳定分析的正确性。

表1 仿真模型的参数

3)当δE>δD时，逆变器的输出有功功率PE

在MATLAB/Simulink中，用仿真验证上述Lyapunov直接法的正确性，结果如图11所示。当故障在0.45 s被清除时，功角δ能回到稳定平衡点A点。当故障在0.55 s被清除时，功角δ能回到平衡点C点。当故障在0.65 s被清除时，系统状态变量发散，无法达到平衡点。仿真结果与Lyapunov直接法的结论相一致。

3.2.2 中度电网故障的情况

中度电网故障下系统的的功角特性曲线如图12所示，当功率给定为Pref，且当系统处于稳态时，工作点稳定在A点，其功角为δA。

在中度电网电压跌落的情况下，逆变电源进入电流饱和模式，由电压源切换为电流源。系统的工作点从A点突变至A′点，且A′点的输出有功功率PE>Pref，由前文的分析可知，此时系统处于减速区域，逆变器的功角将减小，沿着饱和功角特性曲线P(2)移动，最终到达稳定平衡点C′。

故障清除后，系统的工作点将从C′点跳变到C″点。由于C″点的有功功率输出仍然大于Pref，系统仍处于减速区域，逆变器的功角将继续减小并达到饱和功角特性曲线P(1)上的稳定平衡点C。

故障清除的过程，使得系统的稳定平衡点发生切换，导致故障切除前后临界能量发生变化。整个过程的能量与临界能量对比如图13所示，其中Vcr1和Vcr2分别表示故障切除前后的临界能量。由图13可知，故障发生后，系统的能量突增，但没有超过临界能量Vcr1，随后随时间渐渐降低至0，由此判断系统能保持同步稳定。故障切除后，系统的能量远低于临界能量Vcr2，因此仍然能保持稳定。因此，故障切除时间并不会对系统保持同步稳定产生影响。

为了验证上述理论分析，在MATLAB/Simulink平台构建了如图1所示的仿真模型，仿真模型参数配置如表1所示。

仿真结果如图14所示，逆变器正常运行时，工作点为A点。当电网电压幅值U从1.0 pu突降至0.8 pu时，逆变器的功角将持续减小，工作点由A点移动至不稳定平衡点C′。故障清除后，系统将稳定在C点运行，无法返回到A点。仿真结果与结论一致，验证了结论的有效性。

4 提高同步稳定性的优化策略

根据3.2节的分析可知，在电网发生严重故障期间，逆变器输出电流饱和，逆变电源由电压源切换为电流源。由于此时逆变器输出有功功率PE恒小于Pref，系统处于加速区域，功角持续增大，无法达到平衡状态，逆变器发生同步失稳。

3.2节通过Lyapunov直接法构造系统的能量函数，详细分析了故障切除时间对系统同步稳定性的影响。然而，在某些特定的情况下，无法及时切除电网发生的故障，需要采用一些特殊的控制方式使系统保持同步稳定。

针对以上问题，提出一种暂态同步控制策略，在逆变器输出电流饱和阶段，通过将有功调频控制切换为无功调频控制，使故障期间逆变器功角稳定，以此增强系统同步稳定性。

4.1 优化控制策略的描述

图1中线路动态方程为：

(19)

其中：XΣ为网侧滤波电抗与线路电抗之和；LΣ为对应的电感值；RΣ为对应的电阻值，在电路呈感性的条件下，RΣ可忽略不计，并且LΣ≈XΣ。

逆变器输出功率计算方程为：

(20)

电流饱和的情况下，Id=Imax，Iq=0代入式(19)、式(20)可得：

(21)

由式(21)可知，在电流饱和的情况下，逆变器输出无功功率与功角存在一定的数学关系，由此绘制无功功角特性曲线如图15所示。

由图15可知，由于下垂控制中无功-电压下垂部分功率给定值Qref的存在，逆变器稳定工作时，系统的无功工作点稳定在C点。

在重度电压跌落的情况下，逆变电源由电压源切换为电流源，系统发生同步失稳，功角持续增大。无功工作点由C点突变至C′点，且无功功率也会随功角的增大而呈正弦规律振荡，无法保持稳定。

因此，提出一种优化控制策略，具体描述为：故障发生后，在逆变器电流饱和阶段，将有功调频控制切换为无功调频控制，通过给定无功功率限制QL，使逆变器的功角保持稳定，从而使得有功功率不会发生同步失稳。这种控制策略的原理与控制方式如下式和下图所示：

(22)

根据式(22)绘制带有优化控制策略的逆变器饱和功角曲线如图17所示。

由图17可知，故障发生后，逆变器发生饱和切换，进入电流饱和模式，有功工作点由稳定平衡点A′点突变为A′点。由于优化策略的存在，逆变器转为无功功率控制，工作点切换为无功功角特性曲线上的C′点，随后稳定在无功功角特性曲线与无功功率限制QL的交点处，即图中的C″点。由于此时逆变器的功角已趋于稳定，不再变化，因此对应的输出有功功率同样能维持稳定，不发生振荡。有功功率工作点稳定在图中A″点。

4.2 仿真验证

为了验证该策略对提高系统同步稳定性的作用，在MATLAB/Simulink平台构建仿真模型，仿真参数见表1，其中QL=0.5。

仿真结果如图18所示。由图可知，在未添加优化控制的情况下，电网发生故障的瞬间，有功与无功功率均发生突变，并沿着功角特性曲线变化，与前文分析一致。

添加优化控制后的功角特性曲线如图19所示。由图可知，在电网故障后，功率控制方式发生切换，由于添加了无功功率限制QL，使得逆变器输出有功功率与无功功率能保持在一个定值，功角不再发生变化，保持稳定。

综上所述，没有采用优化策略的系统，在电网故障时发生了暂态功角失稳，由于此时不存在平衡点，系统无法保持稳定；而采用优化控制策略后的逆变器，在电网故障后，能使逆变器输出有功功率与无功功率维持恒定。因此，该优化控制策略能提高下垂控制逆变器的功角稳定性。

5 结 论

电网故障下，三相电压源型逆变电源电流指令饱和限幅使得其会发生电压源/电流源模式切换过程，给其同步稳定性带来考验。计及该暂态模式切换影响，首先建立了下垂控制逆变器同步动态动力学模型，分析了电压源/电流源模式切换对其同步动态的影响。进而运用Lyapunov直接法建立了电压源/电流源两种运行模式下系统的暂态能量函数，从加减速面积和系统能量变化的角度分析了电网故障下系统同步稳定性及影响因素，并提出了一种基于功率改进控制的优化控制策略以增强同步稳定性，得到结论如下：

1)重度电网故障的情况下，下垂控制的逆变器故障期间不存在平衡点，发生同步失稳，而根据故障切除时间的不同，切除后系统存在3种不同的工作状态，并且切除时间越长越难保持稳定。

2)中度电网故障的情况下，故障期间系统仍存在稳定平衡点，并且无论何时切除故障，系统总会工作在电流饱和的稳定平衡点。

3)提出的基于功率改进控制的优化控制策略可以解决采用下垂的控制逆变器在电网严重故障下失稳的问题，有效提高系统暂态同步稳定性。