SF6混合绝缘气体的协同效应及其机理研究

沈腾达，郑宇，周文俊，邱睿

(武汉大学 电气与自动化学院，湖北 武汉 430072)

0 引 言

六氟化硫(SF6)气体具有优异的绝缘性能与稳定的化学性质，被广泛应用于电气设备中[1-3]，但SF6气体全球变暖潜势值(global warming potential，GWP)是CO2的23 500倍，在空气中能够存在3 200年，是《巴黎协定》限制排放的6种温室气体之一[4-5]，考虑目前的“碳中和”要求，研究SF6替代气体意义重大。现存几种替代潜力较大的气体虽然具有接近甚至超过SF6的绝缘性能，但都存在液化温度过高的问题，需要混合缓冲气体(如CO2，N2，空气等)来降低液化温度[6-7]；另一种方法就是使用SF6混合气体来降低SF6的使用量，从而降低GWP与液化温度[8-9]。上述两种方法使用到的替代气体均为混合绝缘气体，因此对混合绝缘气体的理论研究十分重要。混合绝缘气体研究，最重要的问题是缓冲气体种类与混合比例对混合绝缘气体性能的影响，而如何选取合适的缓冲气体以及混合比例，协同效应的强弱是十分重要的参考[10-11]。

早在1972年，日本Takuma等人首次提出了协同效应系数计算公式来对协同效应进行定量评估，认为协同效应系数只与混合气体组成类型有关，而不会随混合比例、气压、间隙距离的变化而变化，并使用SF6/N2和SF6/CCl2F2两种混合绝缘气体进行了相关验证[12]，这也是以后的相关研究中使用最为广泛的公式。近年许多学者对混合绝缘气体的协同效应进行了研究：张晓星等人使用上述公式对不同气压、混合比下C4F7N/CO2的协同效应系数进行了计算，并作为使用气压与混合比例选取的参考依据[13]；满林坤等人通过相同的计算公式对不同c-C4F8混合气体在不同混合比与间隙距离下的协同效应系数进行了计算，给出了两种c-C4F8混合气体协同效应系数的范围[14]；张乔根等人提出了归一化系数h代替协同效应系数C，解决了协同效应系数计算公式不能评估负协同效应的问题[15]，这些研究结果中协同效应系数会随试验条件(如缓冲气体种类、混合比例、气压、间隙距离)的变化而变化，虽然计算结果更具有针对性，但是对于不同条件都需要进行相应试验，试验成本和工作量巨大。有必要从理论上对不同混合气体的协同效应进行评估，为开展更有针对性的试验提供参考。

然而，关于混合气体协同效应强弱的理论分析目前较为缺乏，邱毓昌从碰撞截面分布的角度对c-C4F8、SF6与N2、CO、H2的协同效应进行了分析，认为缓冲气体的非弹性碰撞截面在高电子能量时数值较大，可以降低电子速度利于电负性气体吸附[16]；赵谡等人通过碰撞截面对CF3I/N2、CF3I/CO2两种混合气体的电子能量分布、约化净电离系数进行了计算分析，对两种混合气体协同效应强弱进行了对比，但选取的缓冲气体种类较少，两种混合气体的计算结果差异不明显，尚未解释不同缓冲气体协同效应的强弱机理[17]。

由于混合气体种类较多，本文选择了最具有代表性的SF6混合气体进行研究，根据目前已有研究， SF6/N2、SF6/Air(空气)、SF6/CO2、SF6/CF4和SF6/He被视为SF6的潜在替代绝缘气体[18-20]，这5种SF6混合气体具有相对较高的应用价值，因此本文研究上述5种混合绝缘气体在0.4 MPa气压(绝对压力，下同)，0～100%混合比例下在均匀电场中的工频击穿特性，根据试验结果分析了不同缓冲气体和不同混合比例对工频击穿电压的影响，并通过协同效应系数公式对击穿电压的变化曲线进行了拟合，得到的不同混合绝缘气体的协同效应系数，从而对不同缓冲气体与SF6的协同效应强弱进行了对比，从电子能量分布的角度理论分析了不同缓冲气体与SF6的协同效应强弱对比，理论分析结果与试验分析结果一致，为混合绝缘气体选取缓冲气体提供了参考依据。

1 试验装置与方法

1.1 试验平台

本文采用的工频击穿试验回路如图1所示，其中试验变压器额定输入电压为50 Hz，220 V交流电压，额定容量30 kVA；保护电阻为10 kΩ；电容分压器的变比为1 000∶1，电容分压器与电压表经计量院校准，测量误差<1%。提供试验气体环境的试验腔体为不锈钢制成，容积为10 L，最大长期耐受气压为0.7 MPa(绝对压力)，内部电极为平板电极，用于模拟均匀电场，试验时使用环氧树脂支架固定电极并调节电极间距，结构如图2所示。

1.2 试验方法

试验前需要对试验腔体内部进行清洗和对试验电极进行打磨，并用无水酒精清洁电极表面，最后对试验腔体进行正压和负压的气密性检查。试验环境温度保持20 ℃，工频击穿试验的加压方法为逐级升压法，对每一种试验条件，先进行试验得到首次击穿电压Ub0，后续试验以Ub0为基准，先快速升压到Ub0的75%，然后以每秒2%Ub0左右的速度进行升压直至击穿，记录此时的击穿电压，每两次击穿试验间隔至少3 min，以保证气体的绝缘强度得以恢复，每个试验条件下取10个有效数据(数据的相对平方差<5%)。

本文需要对多种SF6混合气体进行0～100%混合比例的工频击穿试验(50%以下间隔为5%，50%以上间隔为10%)，试验量较大，为提高试验效率，减少试验使用的SF6，对混合气体的充气方法进行了优化。以往进行混合绝缘气体的击穿试验，每个比例都需要重新配置气体再进行试验；而根据道尔顿分压定律，混合气体的组分在腔体内的分压相当于它独自存在时的分压，并在腔体内均匀分布，由此采取了混合比例从高到低的配比方法，每次试验不需要重新配置，而是放出一部分混合气体，再充入缓冲气体至试验气压，从而实现混合比例的变化，大大提高了试验效率，具体操作步骤及计算如图3所示。

为了验证优化试验方法不会影响到试验结果的准确性，选取了SF6/N2混合气体，在2.5 mm电极间距，20 ℃环境，0.3 MPa气压下，使用两种不同的配比方法进行验证试验，并对两种方法得到的试验结果进行对比，验证试验结果如图4所示，从试验结果可以看出，两种方法的工频击穿试验结果基本相同，说明了优化的混合气体配比方法的可行性。

2 试验结果与分析

2.1 混合比对SF6混合气体击穿电压的影响

试验对象为SF6/N2、SF6/Air、SF6/CO2、SF6/CF4和SF6/He五种混合气体，试验气压为0.4 MPa(绝对压力)，电极间距为5 mm，SF6的占比为0～100%，考虑到SF6/N2、SF6/Air、SF6/CO2、SF6/CF4在实际应用中为降低液化温度和GWP值，混合气体中SF6的占比一般较低，因此本文对低比例下的击穿电压更为关注，对低于50%的混合比例采取5%为间隔，高于50%的混合比例采取10%为间隔，而SF6/He的应用比例不固定，采取10%为间隔。工频击穿电压的试验结果在图6中有所展示。此外，本文引入了击穿电压相对值，将击穿电压除以同一试验过程中纯SF6的击穿电压，这样可以与纯SF6的绝缘性能进行对比，也可以降低因试验平台引起的误差，从而对5种混合气体进行对比，不同缓冲气体的混合气体的击穿电压相对值如图5所示。

根据图5击穿电压相对值的对比，在仅考虑工频击穿电压的情况下，SF6/N2在5%～80%的比例下击穿电压都是最高，SF6/Air次之，SF6/CO2与SF6/CF4的击穿电压十分接近，SF6/He的击穿电压则远远小于其他4种混合气体。在80%混合比例以后，由于SF6占比较大，此时混合气体的绝缘性能都十分接近纯SF6，不同SF6混合气体之间的击穿电压差距也很小，此时试验误差很容易影响到不同混合气体之间击穿电压的强弱对比，例如SF6/N2的击穿电压在90%混合比例时略低于SF6/Air，但这并不影响对不同SF6混合气体绝缘性能的整体强弱对比。此外，SF6/N2、SF6/Air、SF6/CO2、SF6/CF4混合气体的击穿电压随混合比例增大呈明显的非线性变化，并且击穿电压均在低混合比例时(0～20%)上升较快，随后缓慢上升。与其他4种混合气体明显不同的是，SF6/He的击穿电压随混合比例呈线性变化。如果以80%的SF6绝缘性能为要求，SF6/N2、SF6/Air、SF6/CO2、SF6/CF4和SF6/He分别需要的SF6比例约为20%、35%、45%、50%和75%。

2.2 不同缓冲气体与SF6协同效应的对比

为了能定量对比不同缓冲气体与SF6的协同效应，采取Takuma等人提出的协同效应系数公式对试验结果进行拟合，拟合公式[12]为

(1)

式中：Um为混合比例为k时的击穿电压；U1为SF6的击穿电压；U2为缓冲气体的击穿电压；C为协同效应系数。为降低试验误差的影响，采取击穿电压相对值进行拟合，拟合公式修改为

(2)

式中：Umr和U2r分别为混合气体和缓冲气体纯气的击穿电压相对值。由公式可知，在出现协同效应的情况下，协同效应系数C在0～1的范围内变化，并且C越小，协同效应越强。

拟合结果如图6所示，结果的具体数值如表1所示。

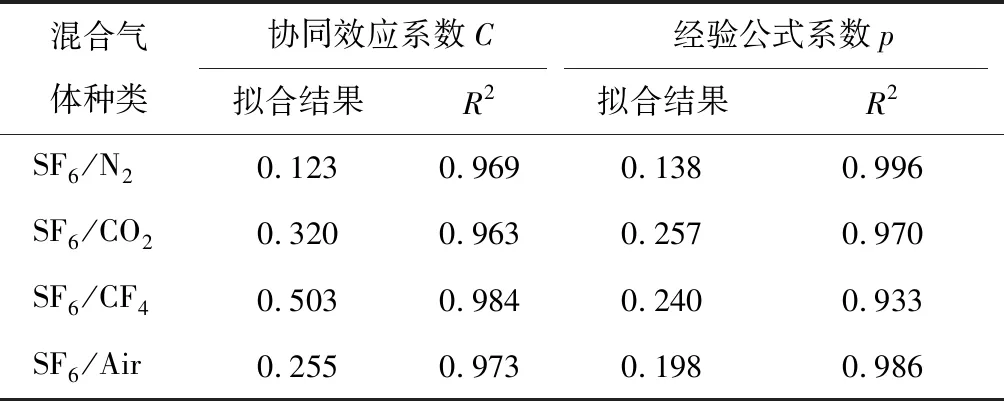
表1 两种拟合公式的拟合结果

为了对拟合结果的效果进行评价，对击穿电压相对值的试验结果同时采取了幂函数经验公式拟合的方式进行对比，拟合公式[21]的形式为

Umr=kp。

(3)

式中p为经验公式拟合得出的结果，经验公式与协同效应系数公式不同，经验公式没有物理意义，仅用于对混合气体击穿电压的预测。

两种拟合方法均采用Levenberg-Marquardt优化算法，具体的试验结果与两种公式的拟合结果如图6所示。从图中可以看出两种拟合方法得到的拟合曲线结果十分接近，表1中的拟合优度R2可以表征拟合效果的好坏，协同效应系数公式拟合曲线的R2均大于0.960，这说明协同效应系数公式的拟合效果较好，经验公式对SF6/N2、SF6/Air、SF6/CO2试验结果的拟合优度R2略高，但在0～5%的混合比例处对SF6/CF4试验结果的经验公式拟合结果明显偏离了试验结果，导致拟合曲线的拟合优度只有0.933，拟合效果较差，而协同效应系数公式的拟合效果好于经验公式拟合，这是由于协同效应系数公式相比经验公式参考了缓冲气体纯气的击穿电压相对值，作为对拟合曲线的拟合结果的限制，从而避免了较大误差的产生。

根据表1中协同效应系数公式的拟合结果C的数值，C数值越小，混合气体的协同效应越强，根据混合气体总体的协同效应系数C对比可以得出，N2与SF6的协同效应最强；空气次于N2，这可能是由于空气中接近百分之八十的成分为N2；CO2与SF6的协同效应弱于N2与空气，但明显优于CF4，SF6/CO2和SF6/CF4击穿电压十分接近的原因是CF4本身绝缘性能很高。

而对于SF6/He混合气体，由于其击穿电压随混合比例的变化接近于线性变化，所以区别于另外4种混合气体，对试验结果进行了线性拟合，拟合优度R2达到了0.993。这说明了混合气体的击穿电压是SF6和He两种纯气击穿电压的线性叠加，对应协同效应系数C为1的情况，这说明两种气体之间没有协同效应。

综合上述对试验结果的整体分析，得出各种缓冲气体与SF6协同效应的强弱对比，由强到弱的排列为：N2>Air>CO2>CF4>He。

3 协同效应机理分析

绝缘气体高绝缘性能的主要来源是对电子的吸附能力，但是对电子的吸附能力不仅取决于绝缘气体本身，也取决于电子的速度。SF6的3种吸附电子碰撞的碰撞截面如图7所示[22]。碰撞截面的大小决定了SF6对电子的吸附能力，可见SF6对分布在 0～1 eV电子能量的电子吸附能力较强，对于更高电子能量，电子的吸附碰撞截面下降了多个数量级，相应的吸附电子的能力也大大下降。缓冲气体降低了电子的速度，使电子更多地分布在低能量区域，使SF6更容易吸附电子，从而提高了混合气体的绝缘性能，从这个角度，可以对不同缓冲气体与绝缘气体协同效应的强弱进行对比。

为获得不同缓冲气体的电子能量分布，采用了BOLSIG+软件对不同缓冲气体的二阶近似Boltzmann方程组进行了求解。考虑到SF6的临界约化场强约为350 Td，分别设定约化场强为140、245和350 Td，对应工频试验结果中的0.4倍到1倍SF6击穿电压。不同缓冲气体的电子能量分布如图8所示。

根据图8中不同缓冲气体电子能量分布，发现在低电子能量区域，在某一电子能量后，分布概率开始快速下降。考虑到SF6的吸附碰撞截面主要分布在0～1 eV，对比了不同缓冲气体在0～1 eV的电子能量分布函数，可以得出电子能量分布概率的大小由高到低为：N2>Air>CO2>CF4>He。电子能量分布在0～1 eV的概率越大，越能发挥SF6的吸附能力，也说明缓冲气体对电子的缓冲能力越强，表现在宏观上，就是与SF6的协同效应越强，混合气体的绝缘性能越高。根据上述分析，可以推断出缓冲气体对电子缓冲能力大小的对比，得到结果为N2>Air>CO2>CF4>He，即与SF6协同效应强弱的对比，与根据工频击穿试验结果得到的与SF6协同效应强弱顺序完全一致，证明了这种理论分析方法的合理性。未来在为新型绝缘气体选取合适的缓冲气体时，可以根据绝缘气体的吸附碰撞截面的分布与不同缓冲气体的电子能量分布，对比得出协同效应更强的缓冲气体。

此外，以N2为例，如图9可以看出随着约化场强的增大，电子在低电子能量的分布概率逐渐降低，这使得SF6的吸附能力降低，协同效应因此降低。反映到击穿电压上，在低混合比例时，混合气体的击穿电压较低，约化场强较低，协同效应高；反之在高混合比例击穿电压较高，约化场强较高，协同效应低，这在一定程度上解释了为什么混合气体的协同效应会随着混合比例的增大而降低。

4 结 论

本文使用优化混合绝缘气体协同效应测试方法，研究了均匀电场下不同SF6混合气体的协同效应的强弱对比并进行了机理分析。主要结论如下：

1)使用协同效应系数公式对不同SF6混合气体的工频击穿试验结果进行了拟合，协同效应系数公式拟合效果良好，并根据拟合结果得出了不同缓冲气体与SF6协同效应的强弱排序：N2>Air>CO2>CF4>He。

2)从绝缘气体吸附分布与缓冲气体电子能量分布的角度分析并解释了不同缓冲气体与SF6协同效应的强弱，电子能量分布在低能量区的概率越大，说明缓冲气体对电子的缓冲能力越强，表现在宏观上，就是与SF6的协同效应越强，混合气体的绝缘性能越高。理论分析得出的协同效应的强弱排序与试验结果一致，证明了这种理论分析方法的合理性。