无轴承电机并联式集成绕组设计准则与快速分相方法

2022-11-18李健李大伟裴同豪曲荣海许湘莲

电机与控制学报 2022年10期

李健，李大伟，裴同豪，曲荣海，许湘莲

(1.华中科技大学强电磁工程与新技术国家重点实验室，湖北武汉 430074； 2.武汉理工大学自动化学院，湖北武汉 430070)

0 引言

无轴承电机具有无摩擦、高转速、高功率密度等优点，尤其适用于航空航天和医药化工等高精尖领域[1-3]。传统的无轴承电机采用定子双绕组结构，由两套绕组分别产生转矩和悬浮力。但是，该结构存在加工难度较高、铜损耗较大、转矩密度较低等问题。相较于双绕组结构，集成绕组结构仅采用一套定子绕组通入两种电流成分，同时产生转矩与悬浮力，有效地解决了上述问题[4]。采用盘状结构的无轴承薄片电机(bearingless permanent magnet slice motor, BPMSM)则进一步简化了无轴承电机的系统结构[5]。

目前，针对无轴承电机已经提出的集成绕组结构主要包括：裂相式、中点电流注入式、桥式与并联式。文献[6-8]针对感应电机提出裂相式结构，该结构将每相绕组分裂为多个部分，并分别控制各部分通入的电流以产生所需要的悬浮力。但是，裂相式结构的控制系统和控制策略较为复杂，难以获得良好的控制性能。文献[9]提出中点电流注入式结构，该结构在每相绕组的中间点处注入悬浮电流，使得气隙磁密只在一侧发生变化而另一侧保持不变。虽然该结构有利于抑制转轴的振动，但其产生的径向悬浮力仅为通常结构的一半。文献[10-11]提出桥式结构，该结构将每相绕组分为两个并联支路，转矩电流分流至各支路，悬浮电流连接在各支路的中点之间。然而，桥式结构需要多组带隔离的单相逆变器，因此控制电路所需的器件增多，设计的成本较高。文献[12]提出并联式结构，该结构与中点电流注入式类似，不同的是，向每相绕组中点注入的是转矩电流而非悬浮电流。该结构仅需两组三相逆变器供电，简化了控制系统。此外，在转子未发生偏移时，悬浮端不存在反电势，减小了控制系统所需供给的电压，桥式结构也同样具有这一特性。因此，文献[13-14]中又将桥式结构与并联式结构统称为无电压式结构。综上所述，本文将重点围绕并联式结构展开无轴承电机集成绕组设计的研究。

就集成绕组的设计方法而言，文献[14]基于槽矢量星形图法给出了可推广的设计流程。该方法具有直观清晰的优点，但整体设计步骤较为复杂。此外，在电机槽数较多时，绘制槽矢量星形图将耗费大量的时间和人力。针对这一问题，本文提出基于槽号相位图的快速并联式集成绕组(parallel combined winding,PCW)设计方法。首先，分析BPMSM主动悬浮力的产生原理并说明其能够实现稳定被动悬浮的特性；其次，依据PCW的结构特点，给出流经各线圈组的电流表达式，并基于此推导PCW的参数选取准则与极槽配合优化准则；然后，分别采用槽矢量星形图法和槽号相位图法进行PCW设计，并将两者的设计流程进行对比，由此说明槽号相位图法绘制简洁、流程简单的优点；最后，将所设计的PCW应用于30槽/4极的表贴式无轴承永磁薄片电机(surface-mouted bearingless permanent magnet slice motor, SM-BPMSM)中，通过电磁转矩和主、被动悬浮力的有限元分析，验证绕组设计的正确性与有效性。

1 BPMSM运行原理

BPMSM的径向主动悬浮力产生原理与传统无轴承电机相同，即依靠励磁磁链与悬浮绕组产生的磁链相互作用实现[15]，其产生条件为：

(1)

式中：ps、pm分别为悬浮磁场极对数、励磁磁场极对数；ωs、ωm分别为悬浮磁动势旋转角频率、励磁磁动势旋转角频率。

不同的是，由于BPMSM结构上长径比较小的特点，其可以依靠磁阻力实现轴向和扭转自由度的被动悬浮[16]，如图1所示。该作用效果体现为：当永磁转子发生沿轴向的运动或出现倾斜时，被动回复力或力矩将其拉回至平衡位置。

2 PCW结构特点与设计准则

2.1 PCW结构特点

PCW电路结构如图2所示，每相绕组均包含两个线圈组，每个线圈组中包含若干个串联线圈，各线圈组的同名端相连。在转子未发生径向偏移时，从注入悬浮电流的端子看去，每相两个线圈组中的感应电势对冲抵消，相当于两个线圈组并联在一起。

PCW中各线圈通入的电流均同时包含转矩电流成分与悬浮电流成分，通过对其电路结构特点的分析，可以得到通入各线圈组的电流情况，表达式为：

(2)

式中：iua～iwb为各线圈组的电流；itu～itw为各相绕组通入的转矩电流；isu～isw为各相绕组通入的悬浮电流。

2.2 PCW设计准则

2.2.1 参数选取准则

PCW结构对无轴承电机的相数m、转子极对数pm、悬浮绕组极对数ps和定子槽数z等参数的选取存在特定的约束条件。

1)相数选取准则。

常规无轴承电机通常是三相结构，此外，还存在单相和其他多相无轴承电机结构。

当相数m满足下式所述条件时，无轴承电机将兼具较好的转矩和悬浮力产生能力：

m=2k+1 orm=6k,k=1,2,…。

(3)

然而，当相数满足下式所述条件时，所设计的无轴承电机可能呈现出单相电机的转矩特性，导致转矩和悬浮力脉动增加[17]，即

m=1 orm=2k,k=1,2,4,5,7,…。

(4)

因此，为确保无轴承电机的性能，应当按照式(3)选择其相数。

2)定子槽数选取准则。

由图2可知，PCW每相绕组包含两个线圈组，而每个线圈组中至少包含一个线圈。因此，每相绕组所含线圈数应至少满足：

(5)

3)转子极对数与悬浮绕组极对数配合准则。

引用单元电机概念说明该条准则[18]，其定义式为：

t=GCD(z,pm)；

(6)

t′=GCD(z,ps)。

(7)

假设采用对称绕组结构，则应将式(5)的条件进一步约束为：

(8)

然而，由于无轴承电机的定子绕组会同时产生极对数为pm、ps的磁动势，因此应在式(8)的基础上增加约束条件：

(9)

对上述约束条件进行简化，假设当m=6k时，将绕组设计成多个对称三相的结构。因此，m=2k+1为普适条件，在此基础上可以将式(8)、式(9)简化为：

(10)

归纳上述参数选取准则，如表1所示。

表1 PCW参数选取准则

2.2.2 极槽配合优化准则

本文以SM-BPMSM为基础，说明设计三相对称PCW时如何选取较优的极槽配合。

对于SM-BPMSM，假设永磁体磁导率接近于真空磁导率μ0，则气隙磁导恒定。因此，永磁磁动势Fm(θ,t)和悬浮绕组磁动势Fs(θ,t)可以表示为：

(11)

式中：ν、μ为各磁动势的谐波次数；φm、φs为各磁动势的初始相位角。

因此，各磁动势在气隙中产生的磁密可以表示为：

(12)

式中δ为气隙长度，假设忽略开槽带来的影响，可以认为气隙长度恒定。

采用麦克斯韦张量法求解径向主动悬浮力，其求解公式为：

(13)

式中R、l分别为转子外径、转子铁心叠长。

仅以Fx为对象进行讨论且令初始相位角均为0，对式(13)进一步化简可得：

(14)

(15)

当ν=μ=1时，电机能够产生恒定的径向悬浮力；而当ν>1时，如果满足特定条件，将会产生悬浮力脉动。因此，有必要对Bm、Bs进行谐波分析，选取各自的主要谐波成分，如表2所示。

表2 PCW磁密谐波分析

将ν=μ=1的两种成分组合记作(m1,s1)，其他组合类似，下文以满足参数选取准则为前提进行分析。

当ps=pm-1,pm≥2时，组合(m1,s1)产生恒定的径向悬浮力。组合(m3,s5)若满足

|3pm-5ps|=1,

(16)

将产生二倍频的悬浮力脉动，即

pm=2。

(17)

同理，组合(m3,s7)若满足式(17)也将产生二倍频的悬浮力脉动。组合(m5,s11)若满足式(17)将产生四倍频的悬浮力脉动。

当ps=pm+1,pm≥1时，类似地，组合(m1,s1)产生恒定的径向悬浮力。组合(m3,s1)若满足下式条件将产生二倍频的悬浮力脉动：

pm=1。

(18)

对比两种可能的情况，当满足ps=pm+1时，仅有一种组合会产生悬浮力脉动，有利于提升电机的悬浮性能。此外，当转子极对数pm较小时，可能会引入较大的悬浮力脉动[19-20]。

然而，BPMSM通常应用于高速、超高速应用场景，若pm选取较大，则基波频率较大，使得逆变电路开关器件的开关频率提高。同时，对于PCW，若选取ps=pm+1，将使绕组端部长度增加，导致其铜损耗增大[21-22]。

因此，实际PCW设计中，往往需要选取ps=pm-1且pm较小的情况。这就要求在选取极槽配合时，保证转矩绕组基波绕组系数尽可能大，同时使悬浮绕组5、7、11次谐波的绕组系数尽可能小。

归纳极槽配合优化准则如下：

1)若重点关注的是悬浮力大小及其脉动，应选取ps=pm+1；若重点关注的是电机的工作效率，应选取ps=pm-1；

2)若所设计电机的额定转速不高，应选取pm≥4，以降低悬浮力脉动；

3)若电机需要运行于高速工况，应选取pm≤2且合理选取定子槽数，使开关频率不至于过高、转矩绕组基波绕组系数尽可能大、悬浮绕组5、7、11次谐波的绕组系数尽可能小。

2.3 PCW设计准则实施示例

本文以一个pm=2的三相对称PCW为例，说明所述准则的实施过程。

首先，依据式(1)与式(10)得出ps=1；

其次，依据式(5)得出z=6k,k=1,2,…；

然后，依据式(17)将产生二倍频、四倍频等悬浮力脉动，应该选择合适的槽数使悬浮绕组5、7、11次谐波尽可能地小。在z≤30范围内，分析可能的情况所对应的各次谐波绕组系数，如表3所示(各次谐波的单元格中，上为转矩绕组系数，下为悬浮绕组系数)。可以看出，选取z=30时，电机将兼具较好的转矩和悬浮力产生能力。

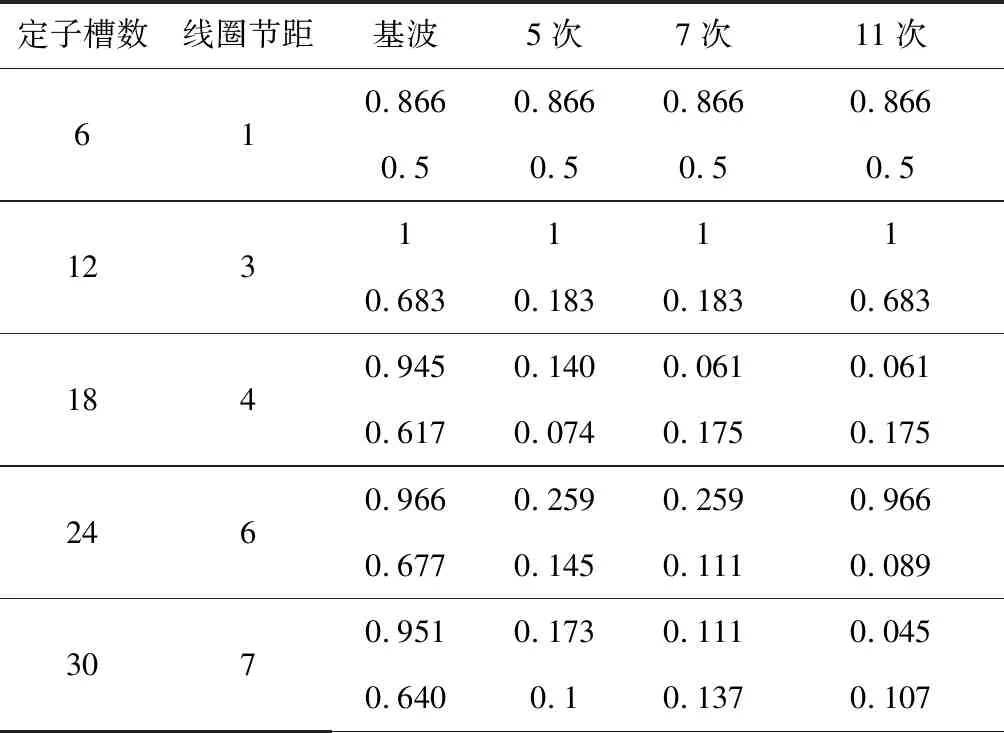
表3 各次谐波绕组系数

3 PCW快速分相方法

在按照所述设计准则确定电机的基本参数之后，需要确定每个线圈中通入的转矩电流相位与悬浮电流相位，即对PCW进行分相。

3.1 槽矢量星形图法

已有的PCW分相方法通过绘制槽矢量星形图实现转子极对数到悬浮绕组极对数的变换，得到各线圈中的电流相位，如图3所示。采用上文设计示例中给出的参数，说明该方法的具体实现步骤。

首先，绘制pm=2对应的槽矢量星形图和连接图(考虑线圈中电流方向的星形图)，相邻槽号矢量之间的夹角为24°电角度，并按照60°相带进行绕组的分相。

其次，绘制ps=1对应的槽矢量星形图和连接图，并按照上述分相的结果进行标注。

最后，依据式(1)对各线圈组中电流情况的分析，需要在保证绕组三相对称的前提下，将ps=1槽矢量连接图中的一半槽矢量反向，如图3(e)中虚线所示，得到悬浮绕组中各线圈实际通入电流的相位情况。为便于理解，未改变图3(f)反向后槽矢量的正负号，但其中通入的电流方向已与原来相反。

对比图3(b)与图3(f)可以发现，pm=2时PCW的三相绕组排布与ps=1时对应的相序相反。此外，在选取一半的槽矢量进行反向时，可能会存在多种选择，应在确保对称性的前提下，选取使悬浮绕组的绕组系数较高的组合。

在完成上述步骤后，可以确定各线圈中通入的转矩电流相位和悬浮电流相位，即可以将各线圈分配至对应的线圈组中，分配的原则是：反向后的线圈放至ua～wa，其余线圈放至ub～wb；每相两个线圈组的矢量之和相等。分配的结果如表4所示。

3.2 槽号相位图法

本文提出一种基于槽号相位图法的PCW分相方法，该方法仅需绘制pm=2、ps=1对应的两张槽号相位图，同时避免了槽数较多时槽矢量星形图存在的矢量分布过密、绘制难度增加等问题。

此外，在选取反向的线圈时，利用槽号相位图可以直接通过图中的小格位移确定对应的槽号。进一步地，可以将该过程归纳为程序代码，快速实现PCW分相，进一步简化PCW的设计流程。

3.3 槽号相位图法实施示例

首先，计算pm=2对应的槽号相位图的基本参数。其横行数为2pm=4，每一横行跨360°电角度；每一横行含小格数为30；相邻槽号在图中的位移小格数为2；同一槽号正负两格之间相差180°电角度。绘制对应的槽号相位图并进行三相分相，如图4所示。

其次，计算ps=1对应的槽号相位图的基本参数。其横行数变为2ps=2；每一横行所含小格数仍为30；相邻槽号在图中的位移格数变为1。绘制对应的槽号相位图，按照上述分相结果进行标注。

然后，选定u相反向的线圈为：-24,-25,1,2,3。v相滞后u相120°电角度(即图中左移10格)，则其反向的线圈为：-14,-15,21,22,23。w相超前u相120°电角度(即图中右移10格)，则其反向的线圈为：-4,-5,11,12,13。最终的线圈分配情况如表5所示。

表5 绕组线圈分配情况(基于槽号相位图法)

需要说明的是，虽然两种方法下线圈分配的结果略有不同，但最终构成的绕组完全等效。

4 SM-BPMSM性能分析

4.1 电机结构参数

本文将所设计的PCW应用于三相SM-BPMSM中，其二维截面图与三维剖面图(不考虑绕组端部)如图5所示，各参数如表6所示。

4.2 电磁性能与主动悬浮性能仿真分析

由于PCW每个线圈中都同时含有转矩电流成分和悬浮电流成分，因此本文将分别讨论只通入转矩或悬浮电流的情况(下称为单电流工况)和同时通入两种电流的情况(下称为双电流工况)。

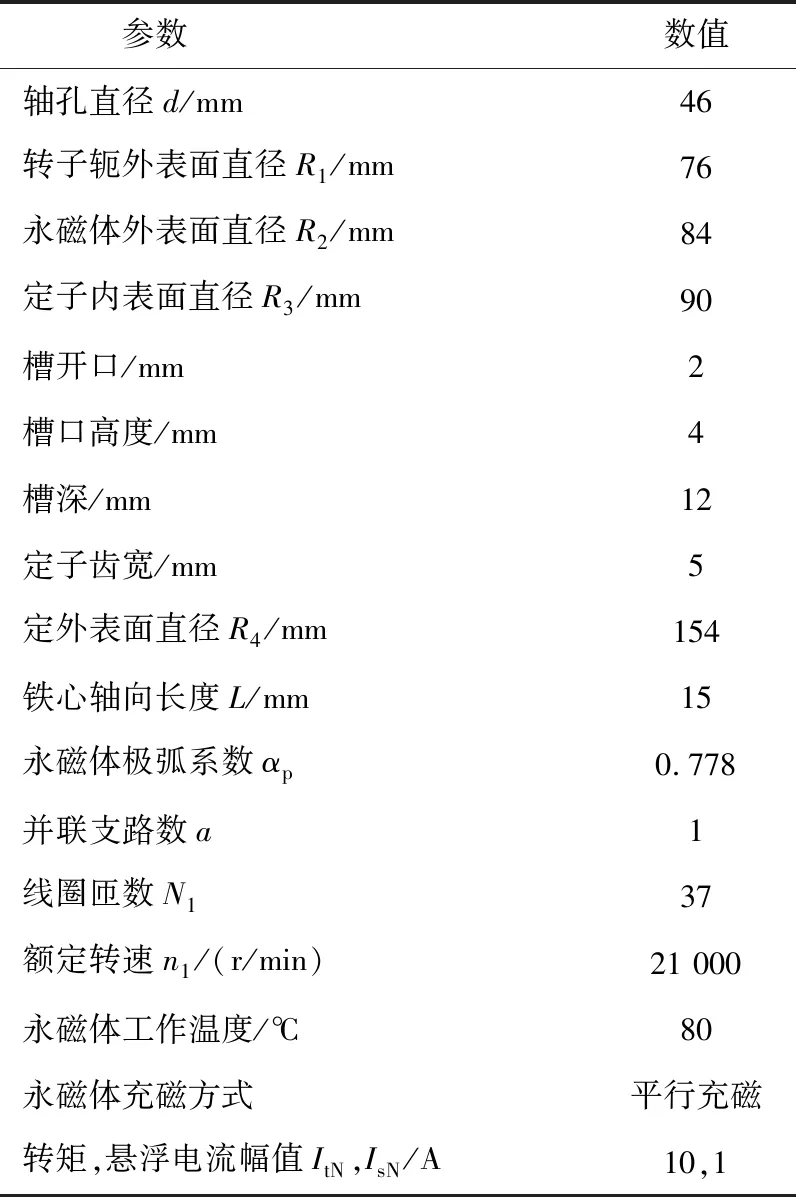
表6 SM-BPMSM电机参数

4.2.1 单电流工况

首先，只通入10 A的正序转矩电流，验证所设计SM-BPMSM产生转矩的能力，通过JMAG有限元仿真分析得到结果如图6(a)所示。转矩平均值约为4.5 N·m，转矩脉动约3.6%。

其次，只通入1 A的负序悬浮电流，验证电机的主动悬浮性能。仿真得到X、Y方向的主动悬浮力如图6(b)所示，合成悬浮力平均值约为13 N，约6.8%。为验证悬浮力的主动可控性，调整悬浮电流相位角使悬浮力大小不变、方向发生改变，其运动轨迹呈圆形，如图6(c)所示。再改变悬浮电流大小，验证悬浮力与其之间的线性关系，结果如图6(d)所示。

对所得主动悬浮力进行FFT谐波分析，得到主要谐波的含量，如图7所示。可以看出，最主要的谐波是二倍频成分，但经过本文的优化设计，其占比较小，验证了上述设计与优化准则的正确性。

4.2.2 双电流工况

保持悬浮电流初始相位角不变，同时通入转矩电流和悬浮电流，仿真结果如图8所示。

对比图6可知：双电流工况下SM-BPMSM的转矩几乎不变，但是悬浮力的大小和方向发生变化，平均值约为12.8 N，脉动增大至接近10%。

据此可以得出，悬浮电流的加入对转矩的产生几乎没有影响，而转矩电流的加入对主动悬浮力的产生具有较大的影响。该问题出现的原因主要有两个，一是转矩电流引起的电枢反应使得磁力线产生偏移，二是潜在的饱和效应引入了更多的谐波成分。

通过上述单/双电流工况下的仿真分析，可以证明本文设计的采用PCW的SM-BPMSM能够同时产生较大的电磁转矩和稳定可控的主动悬浮力[23-24]。