新型同步磁阻电机星形转子结构设计与分析

刘荣哲，董砚，梁晶

(1.河北工业大学 人工智能与数据科学学院，天津 300130； 2.河北工业大学 电气工程学院，天津 300130)

0 引 言

同步磁阻电机转子没有绕组和永磁体，转子惯性小，成本低、结构简单[1]，相对于感应电机具有更高的效率，更低的转子温度，更坚固的结构和出色的瞬态过载能力[2-4]，所以可以作为感应电机的替代品，在多种应用场合中越来越受到关注。由于转子的各向异性，同步磁阻电机表现出较宽的调速范围，非常适合高速和恶劣环境应用[5-6]。

目前，同步磁阻电机的转子磁障结构一般分为分段式，流线形，圆形。文献[7]对比分析了圆形转子结构和分段式转子结构，在相同裂比系数和磁障层数的条件下，圆形转子结构在转矩密度和对应的转矩脉动上的表现均优于分段式转子结构。文献[8]研究表明分段式转子结构的局部饱和和漏磁现象较圆形转子结构严重，导致分段式结构的平均扭矩和效率比圆形结构略低。文献[9]提出了一种流线形转子结构非线性分析模型，结果表明该模型可以根据转子几何形状的变化推导出相应的平均转矩和谐波变化。文献[10]研究了流线形转子磁障末端和q轴轴线的夹角对转矩脉动的影响且推导出一个模型，该模型可以快速选择产生最小转矩脉动的夹角。但流线型公式复杂，对工艺加工水平要求较高。综上原因，学者们研究圆形转子结构较多。

文献[11]对圆形转子结构进行了保形映射变换，可以精确的计算转子磁障磁阻，并且建立磁路等效模型进行了转矩的计算和预测。文献[12]在圆形转子结构磁障位置增加了凸起结构，并通过分析模型得到了四层磁障结构的外面两层磁障凸起结构对磁阻影响不大的结论，同时对内两层磁障凸起结构进行了解析优化。文献[13]基于圆形对称转子磁障结构设计了一种结合电磁、结构和热分析的迭代设计方法，该方法可快速设计出具有低转矩脉动和最小二阶振动模型的同步磁阻电机。文献[14]提出并验证了一种新的同步磁阻电机设计方法，即在解析过程中考虑BH曲线的饱和段及对传统有限元方法进行了改进，结果表明该方法可以大大减小转矩性能解析预测的误差，改进的有限元方法呈现了准确性和鲁棒性。文献[15]提出了一种使用基本电磁方程的同步磁阻电机建模分析方法，将磁障转化成等效气隙长度并添加相应极距的气隙中，将额外气隙长度相加以获得整体气隙函数，并用麦克斯韦张量法预测电磁转矩波形。

同步磁阻电机的转子磁障末端的张角影响着电机的性能，适当增大转子磁障末端张角有助于提高转矩性能[16]。但学者们没有研究传统圆形转子结构增大磁障末端角带来的优异性能，所以本文在传统圆形转子结构的基础上进一步增大转子磁障末端张角，因此提出了星形转子结构。并且对电机进行建模，对转矩进行预测及电机性能分析，验证了星形转子结构出色的电机性能，表明该结构具有实际研究意义。

1 星形转子拓扑结构与建模

1.1 转子结构

提出的星形转子结构如图1(a)所示，图1(b)为圆形转子结构。两种形状的转子均选用3层绝缘磁障。如图1(c)所示，星形转子结构的磁障末端到q轴夹角δ1大于圆形转子结构的磁障末端到q轴夹角δ2。

星形线定义：在平面内存在两个圆，一个定圆(半径为r)和一个动圆(半径为r/4)，动圆绕着定圆内侧旋转一周，并且在运动过程中保证两圆相切，动圆上一定点的运动轨迹即为星形线，如图2所示，P′、P″为动圆上定点P运动过程中的轨迹点。α为OO′与x正半轴的夹角，θ为OP′与x正半轴的夹角，即空气磁障末端角。

其中，以定圆圆心为原点O建立直角坐标系，如图2所示，定圆方程为

x2+y2=r2。

(1)

动圆圆心O′满足

x2+y2=(3r/4)2。

(2)

连接O′P′，根据星形线定义有

PQ=P′KQ。

(3)

式中K为优弧辅助点，并且有

αr=(π+∠P′O′O)r/4。

(4)

根据余弦定理有

(5)

式中：∣O′P′∣=r/4；∣O′O∣=3r。

联立式(4)和式(5)得

(6)

P′点坐标(x,y)可以表示为：

(7)

式中τ为O′P′与x轴正半轴的夹角

τ+α+∠P′O′Q=π。

(8)

联立式(1)～式(8)得星形线参数方程为：

(9)

即星形线方程为：

(10)

又

x=∣O′P′∣cosθ。

(11)

联立式(6)、式(9)及式(11)有

(12)

根据式(12)可以解方程得到α与θ的关系为

(13)

1.2 等效磁路模型

同步磁阻电机磁路分析模型如图3所示，将电机分成6个区域，分别标记为11、12、13、21、31、32、33，并由磁障的末端中点为界限，在模型分析中，忽略磁饱和的情况，且假设在转子铁磁材料中磁动势无变化。

磁动势方程为

F(t,ζ)=∑n=1,2,3ωn(ζ)in(t)。

(14)

式中：n为相位(1表示A相，2表示B相，3表示C相)；ζ是以定子A相轴线s轴为基准沿着气隙的角位置(以弧度为单位)；in(t)表示t时刻的n相电流，且有：

(15)

(16)

(17)

式中：φ0是任意初始相位；I0是相位峰值电流；Ns是每个线圈的串联匝数；b是每相并联支路数；υ表示线圈与极距比；q为每极每相槽数；αs为槽距角，且αs=2πp/Z；p为极对数；Z为定子槽数。

由式(14)～式(17)确定了气隙磁动势，可以计算图3中各个区域的气隙磁动势为：

(18)

(19)

(20)

(21)

(22)

式中：ζr为转子q轴与定子A相轴线的夹角；β1、β2、β3表示第1、第2及第3层磁障末端与q轴的夹角；当p=2，定义θi为第i条磁障曲线的磁障末端角，有θi=βi+π/4且根据式(13)有

αi=arccos(((3cos2θi-(9cos2θi(cos2θi-1)×

(1-…3cos2θi))1/3-(27cos4θi(1-cos2θi))1/3)/3)1/2)。

(23)

式中αi为第i条磁障曲线的参数角。

气隙磁阻计算为：

(24)

(25)

(26)

(27)

式中：μ0为磁导率；δ为气隙厚度；R为转子外径；L为电机轴长。

磁障曲线弧长公式为

(28)

式中si(i=1,2,3)为第i层空气磁障的弧长。

空气磁障磁阻计算为

(29)

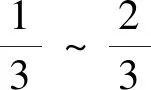
对电机结构进行分析，根据图3的分区，建立如图4所示的等效磁路图。根据等效磁路图进行下列计算。

磁障的磁通量计算：

(30)

(31)

(32)

磁障的磁压降计算：

ΔF1(t,ζr)=φb1Rb1；

(33)

ΔF2(t,ζr)=φb2Rb2；

(34)

ΔF3(t,ζr)=φb3Rb3。

(35)

式中：ΔFi为第i(i=1,2,3)层磁障的磁压降。磁障的磁压降与磁力线穿过磁障的路径无关且在硅钢片中磁动势保持不变。

气隙磁密的计算为：

磁力线穿过不同的磁障形成不同的磁回路，定义ζp为磁力线穿过mi(mi=0,1,2,3)层磁障时所形成的磁回路在穿过气隙时的角度变化量。

1)当磁力线通过第一、二、三层磁障时：

Bδ(t,ζp,ζr)=(μ0/δ)[F(t,ζp)-ΔF1(t,ζr)-…

ΔF2(t,ζr)-ΔF3(t,ζr)]。

(36)

式中ζr-β1p≤ζp≤ζr+β1p。

Bδ(t,ζp,ζr)=(μ0/δ)[F(t,ζp)+ΔF1(t,ζr)+…

ΔF2(t,ζr)+ΔF3(t,ζr)]。

(37)

式中ζr-α1p+2π≤ζp≤ζr+α1p+2π。

2)当磁力线通过第二、三层磁障时：

Bδ(t,ζp,ζr)=(μ0/δ)[F(t,ζp)-ΔF2(t,ζr)-…

ΔF3(t,ζr)]。

(38)

式中ζr-α2p≤ζp≤ζr-α1p或ζr+α1p≤…ζp≤ζr+α2p。

Bδ(t,ζp,ζr)=(μ0/δ)[F(t,ζp)+ΔF2(t,ζr)+…

ΔF3(t,ζr)]。

(39)

式中ζr-α2p+2π≤ζp≤ζr-α1p+2π或ζr+α1p+2π≤ζp≤ζr+α2p+2π。

3)当磁力线通过第三层磁障时：

Bδ(t,ζp,ζr)=(μ0/δ)[F(t,ζp)-ΔF3(t,ζr)]。

(40)

式中ζr-α3p≤ζp≤ζr-α2p或ζr+α2p≤…ζp≤ζr+α3p。

Bδ(t,ζp,ζr)=(μ0/δ)[F(t,ζp)+

ΔF3(t,ζr)]。

(41)

式中：ζr-α3p+2π≤ζp≤ζr-α2p+2π或ζr+α2p+2π≤ζp≤ζr+α3p+2π。

4)当磁力线通过转子但不穿过磁障时：

Bδ(t,ζp,ζr)=(μ0/δ)F(t,ζp)。

(42)

式中ζr-π/p≤ζp≤ζr-α3p或ζr+α3p≤…ζp≤ζr+π/p或ζr-π/p+2π≤ζp≤ζr-…α3p+2π或ζr+α3p+2π≤ζp≤ζr+π/p+2π。

在忽略磁饱和和齿槽效应的前提下，转矩计算为

Tem(t,ζr)=-∂Wm(t,ζr)/∂ζr。

(43)

式中Wm为电机存储的总磁能。

Wm(t,ζr)=Wmg(t,ζr)+Wmb(t,ζr)。

(44)

式中：Wmg为储存在气隙中的磁能；Wmb为储存在磁障中的磁能(在磁导率较大时，假设在转子铁磁部分不储存磁能)。

(45)

式中Rm=d2+δ/2为平均气隙半径。

Wmb(t,ζr)=p(Rb1φb1(t,ζr)2+Rb1φb2(t,ζr)2+…

Rb3φb3(t,ζr)2)。

(46)

将式(44)～式(46)代入式(43)中，得到转矩计算结果。

1.3 有限元仿真验证

通过二维有限元软件建立仿真模型，分析验证三相4极24槽星形线转子结构同步磁阻电机和圆形转子结构同步磁阻电机的转矩，电机主要参数如表1所示。

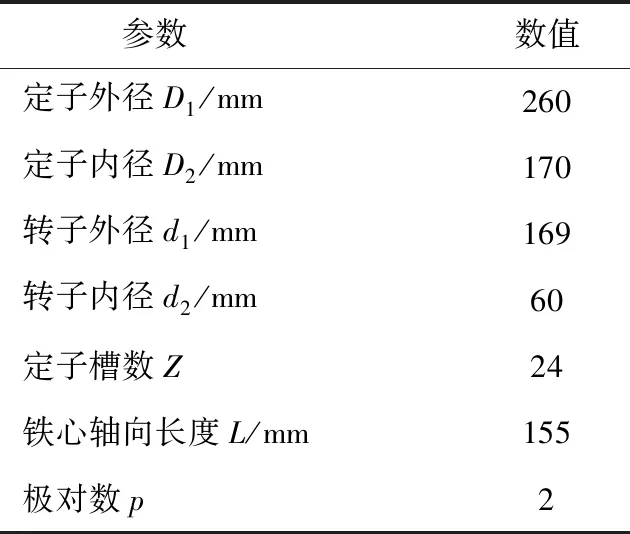
表1 电机主要参数

图5为不同ζr角度下的转矩图。根据图5所示可以看出，在不同的转子位置得到的计算值对比结果误差很小，基本吻合，在可接受范围内，验证了解析计算模型的准确性。

2 电磁性能分析

根据表1的参数，建立有限元模型如图6所示，对两种转子结构同步磁阻电机性能对比分析。

2.1 电机铁耗分析

图7和图8分别为星形转子结构同步磁阻电机和圆形转子结构同步磁阻电机的磁密云图和铁耗曲线图。

从图中可以看到星形线转子的齿、轭处的磁密明显低于圆形转子结构的齿、轭处的磁密，且星形转子的铁心外侧磁密明显低于圆形转子，有利于降低铁耗。由图8可以计算出，前者的铁耗平均值为447.1 W，低于后者的479.7 W。表明星形转子结构有利于提高电机的效率。

2.2 电机空载气隙磁密分析

在额定转速下，对电机空载气隙磁密进行分析和傅里叶分解。图9和图10分别为电机的气隙磁密图和傅里叶分解分布图。

从图中可以看出，两种转子结构同步磁阻电机空载气隙磁密基波幅值基本相同，第5次至第17次奇次谐波影响较小，星形转子结构的第3次、第19次和第21次谐波明显低于圆形转子结构，且星形转子结构的气隙磁密谐波畸变率THD为4.34%低于圆形转子结构的6.39%，表明星形转子结构气隙磁密正弦化程度高，有利于降低转矩脉动。

2.3 电机转矩分析

电机转矩反映了电机输出能力，转矩脉动反映了电机输出的稳定性，两者是电机性能的两个重要指标，图11是两种转子结构的转矩图。

由图11可知，星形线转子结构的转矩平均值为225.3 N·m，高于圆形转子结构的215.1 N·m，且前者的转矩脉动较后者低78%。

从以上验证结果可以看出，文中提出的星形转子结构同步磁阻电机性能优于传统圆形转子结构同步磁阻电机。

3 结 论

本文提出了同步磁阻电机星形转子结构，对星形曲线进行了数学方程推导，进而建立了电机转矩模型，并且与圆形转子结构进行了对比分析，得到了以下结论：

1)通过解析法与仿真结果的对比，验证了转矩模型的正确性。

2)以三相4极24槽同步磁阻电机为例，在保证其他条件一致的情况下与传统圆形转子结构进行对比分析。对磁密云图及铁损分析，结果表明星形转子结构靠近转轴的地方磁密较圆形转子结构更低，有利于降低铁损，铁损降低了32.6 W；对空载气隙磁密分析，结果表明星形转子结构气隙磁密的谐波畸变率较圆形转子结构低2.05%，表明星形转子结构气隙磁密正弦化程度高；对转矩进行分析，结果表明星形转子结构平均转矩较圆形转子结构高10.2 N·m，且转矩脉动降低78%。

3)文中所提出的星形转子结构同步磁阻电机为同步磁阻电机及铁氧体辅助式同步磁阻电机的设计提供了新的选择，具有工程实用价值。