同步发电机转子电磁暂态的准确表达

李生虎

(合肥工业大学 电气与自动化工程学院， 合肥 230009)

同步发电机SG(Synchronous Generator)是电力系统中最重要有功/无功电源。SG功角失稳和频率失稳，是电力系统最严重安全问题。由于方程多、表达形式复杂，SG动态建模，是电力系统动态仿真和稳定分析的基础，也是电力系统暂态分析教学难点之一。

站在SG角度，对其建模可以采用瞬时量形式、abc静止坐标系。站在电网角度，SG建模一般基于相量形式、派克变换后dq旋转坐标系，借助机网结构方程，与电网xy坐标系方程联立求解。

SG电磁暂态包括定子暂态和转子暂态。定子暂态为2阶方程，衰减较快，可简化为代数方程。转子电磁暂态考虑励磁绕组(f)和阻尼绕组(D, Q)，大多用3阶模型描述。

采用磁链作为状态变量时，SG电磁暂态描述非常简单直接。但是由于研究人员更习惯采用内电势(包括d轴暂态电势Eq′和d、q轴次暂态电势Ed″和Eq″)来描述SG，需要转换方程形式，确定暂态和次暂态电抗，增加了电磁暂态准确表达的难度。

现有专著和教材中，有些从电网稳定分析角度考虑，直接给出电磁暂态模型[1-3]。有些基于拓展电路表达和假设条件，尝试给出电磁暂态表达的推导过程，例如：

(1) 根据定、转子电压方程，可将电抗视为电阻、将电阻除以拉式算子后视为等效电容[4-5]；或保留电抗对时间导数，绘制磁链耦合路径，得到d、q轴等效电路[6]。

(2) 对于故障后从定子侧看进去的等效电感，通过不同时间的磁通路径[7]，描述得到暂态/次暂态电感表达。

(3) 基于电压方程或者等效电路，可以得到dq轴运算电抗的拉式变换形式。忽略绕组电阻(人为绕组是超导体)、或者采用初值定理(适用于故障后瞬间)，可以得到暂态/次暂态电抗表达形式[4-7]。

(4) 基于短路试验原理，当f绕组短路、D绕组开路时，令定子绕组中突然流过只含有d轴分量的电流，此时测得定子电抗即是Xd′。当f、D绕组都短路时，令定子绕组中突然流过只含有d轴分量的电流，此时测得的定子绕组电抗即是Xd″。类似可定义Xq″[8]。

SG电磁暂态推导过程涉及很多公式，较为晦涩难懂。因此在讲授本科“电力系统暂态分析”、本科/研究生“电力系统故障分析”、研究生“高等电力系统分析”课程时，对SG电磁暂态建模，往往直接给出最后结果，不解释中间过程。学生常存在疑问：

(1) 暂态/次暂态电抗/电势定义，往往基于等效电路和运算电抗，给人印象是在解释而非严格证明。采用初值/终值定理，不能明确其他时刻暂态/次暂态电抗取值。引入超导体概念，人为假设过强。因此常有疑问：暂态/次暂态电抗/电势表达，是否唯一？

(2) 不同文献中，转子电磁暂态(电压方程)存在不同形式。由此常有疑问：何为准确表达？

针对上述问题，本文基于定转子回路电压/磁链方程，通过矩阵变换，严格证明暂态/次暂态电感/电势表达方式唯一。提出基于内电势的转子电磁暂态的精确表达。算例分析中对比转子电磁暂态系数项，量化了现有近似表达的误差。

1 SG电磁暂态现有表达

正常情况下SG结构和运行参数对称，其结构见图1，内部绕组见图2，其中定子三相绕组和转子励磁绕组实际存在，转子阻尼绕组为等值绕组。

图1 同步发电机结构

图2 同步发电机绕组

忽略零轴、谐波、磁链饱和，将参数由三相静止坐标系变换到dq旋转坐标系，取标么值，定、转子磁链方程见(1)(2)式，电压方程见(3)(4)式。

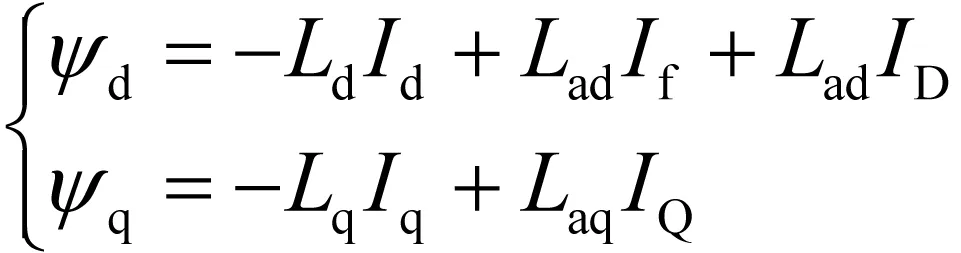
(1)

(2)

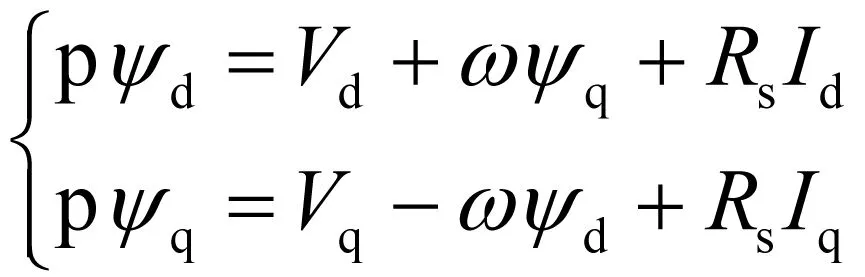
(3)

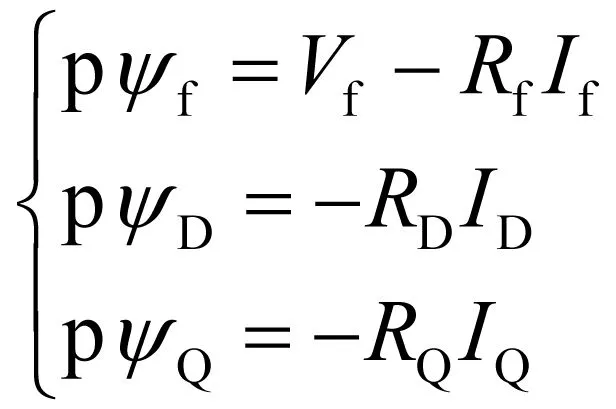
(4)

其中V、I、ψ分别为电压、电流和磁链，R为电阻，L为电感，Lad和Laq为d、q轴反应电感，ω为转速，p为微分算子，下标D表示定子。

在额定转速下，L和电抗X标么值相等。计及机械暂态后，转速存在变化。为简化表达，很多文献不严格区分两者，直接将L写成X。

(3)(4)式可以准确表达SG电磁暂态。其状态变量取磁链，现有计算更习惯内电势模型。将(1)式代入(3)式，得定子电磁暂态简化表达：

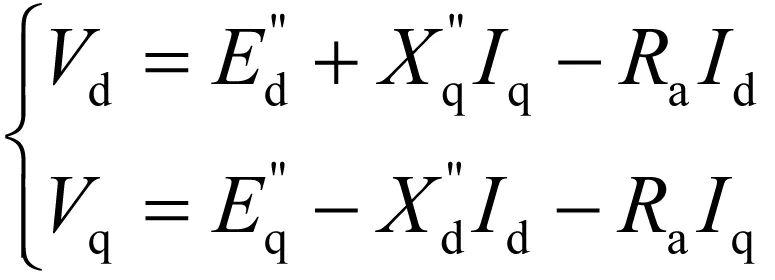
(5)

将(2)式代入(4)式，取状态变量Eq′、Eq″和Ed″，得到定、转子电磁暂态常见近似表达[6, 9, 10]：

(6)

其中Ef=XadIf=XadVf/Rf，Tdo′和Tdo″是暂态和次暂态直轴开路时间常数，Tqo″是暂态和次暂态交轴开路时间常数(7)式。(6)式第二行中pEq′项经常被忽略。

(7)

暂态/次暂态电抗定义见(8)式，暂态/次暂态电势定义见(9)式。

(8)

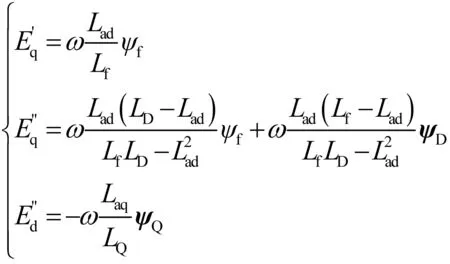
(9)

以下证明：转子磁链暂态(6)式，是否为准确表达、暂态/次暂态电抗和电势(8)(9)式，是否是唯一表达。

2 暂态/次暂态电抗/电势表达唯一性证明

以下基于矩阵变换，提出暂态/次暂态电感/电势的准确表达，以证明其唯一性。

2.1 暂态/次暂态电抗表达唯一性证明

区分定、转子，将(1)-(4)式改写为矩阵形式[11]，

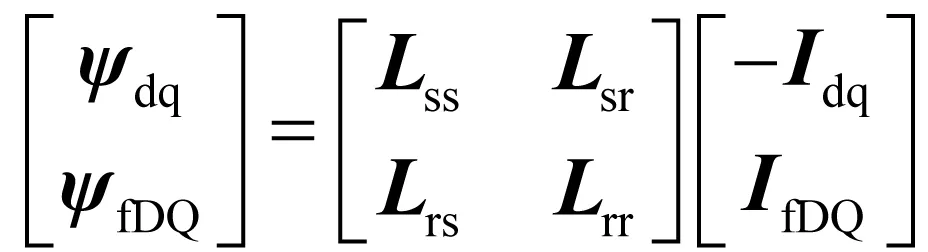
(10)

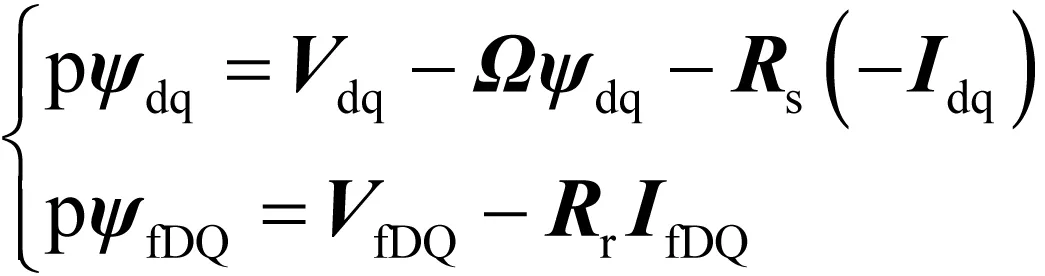
(11)

将-Idq和ψdq对调得，

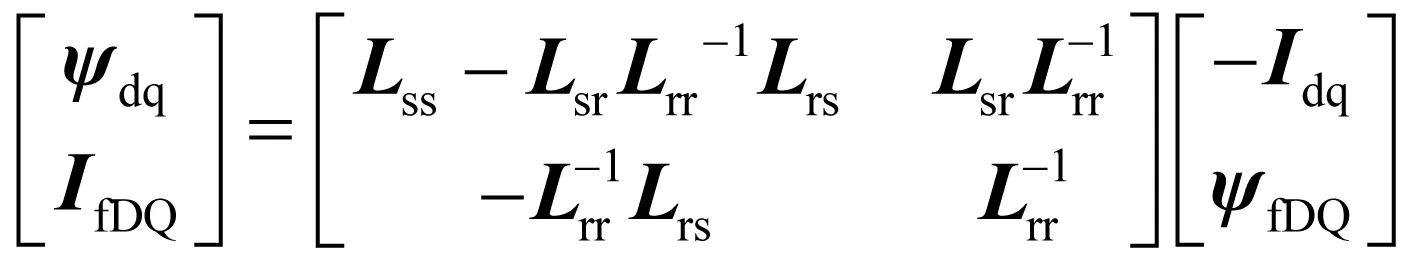
(12)

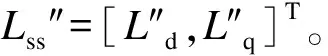
以上表明暂态/次暂态电感表达形式唯一，且不随时间变化，不是仅存在于故障瞬间。没有引入初值定理、超导体等假设，所以是严格证明。

2.2 暂态/次暂态电势表达唯一性证明

将(12)式代入(11)式，得电磁暂态模型，

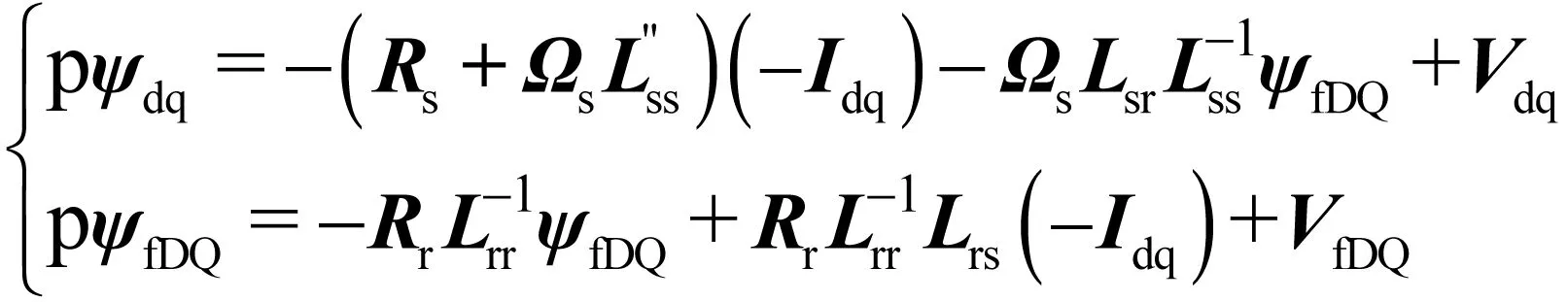
(13)

其中VfDQ=[Vf, 0, 0]T。第一行为机网接口，第二行反映转子电磁暂态。第一行ΩsLsrLrr-1ΨfDQ项展开：

(14)

显然就是(9)式后两行。保留励磁绕组、忽略阻尼绕组，类似可得到(9)式第一行。由此可严格证明，暂态/次暂态电势与转速成正比，且表达方式唯一。

计及(14)式，得定子暂态准确表达：

(15)

对比发现，定子暂态简化表达(5)式忽略定子磁链暂态和转速变化，即假设pψd=pψq=0、ω=1pu[12]。如果计及pψd和pψq，在功角曲线开始阶段中将出现反摆，类似水轮机水锤效应。Kundur、Krause等国内外专家认为，忽略定子磁链暂态和忽略转速变化对SG电磁暂态的影响，可以相互抵消[2, 13]。但是作者严格证明，上述影响可以相互抵消，仅限于定子电阻为零且小扰动分析[14]；否则该结论错误。

3 转子电磁暂态表达的准确表达

相对而言，定子电磁暂态推导较为容易，而转子电磁暂态更难理解，现有表达形式也更多，缺乏准确表达形式。

3.1 转子电磁暂态准确表达

以下基于矩阵变换，提出转子电磁暂态的准确表达。将(9)式写成矩阵形式，

(16)

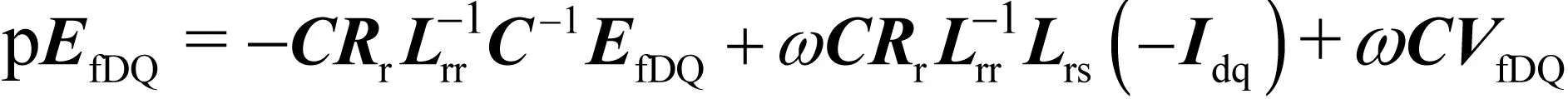
(17)

为比较与(6)式差异，使得右侧转子暂态/次暂态电势项形式接近，改写上式得：

(18)

3.2 现有转子电磁暂态表达的误差

取SG参数Rs=0.003 pu，Ld=1.81 pu，Lq=1.76 pu，定子漏感Ll=0.15 pu，Ld′=0.3 pu，Ld″=0.23 pu，Lq″=0.25 pu，Tdo′=8.0 pu，Tdo″=0.03 s，Tqo″=0.07 s[2]。

定子暂态表示为：

(19)

转子电磁暂态近似表达展开为：

(20)

以下计算SG参数，以建立准确表达。

计算(13)式中系数矩阵：

按3.1节步骤，得到转子电磁暂态的准确表达：

(21)

对比(20)(21)式发现，两式右侧相同，第三行也相同。现有表达的误差，在于左侧时间常数前两行的耦合项。

现有模型忽略第一行pEq′项，是因为其相对于pEq″项衰减较快。将第二行左侧两个系数都取Tdo″、甚至忽略第一项，以简化表达转子电磁暂态表达形式。这些简化节省计算量，但是影响暂态过程的模式特征和衰减速度。

4 结语

本文基于定转子回路电压/磁链方程，通过矩阵变换，证明暂态/次暂态电感/电势表达形式的唯一性，提出基于内电势的转子电磁暂态准确表达。研究发现：

(1) 暂态和次暂态电感表达方式唯一，不依赖于短路瞬间或超导体等人为假设。

(2) 暂态和次暂态电势表达方式唯一。

(3) 现有转子电磁暂态简化表达中，d轴电压方程时间常数存在误差。

上述研究成果，有助于改进电网稳定分析结果的准确性。由于推导过程简洁严谨，便于在本科和研究生教学中得以应用。