“双减”政策下的小学数学高年级试题变化的思考
2022-11-15江畅
江 畅
(福州市鼓楼第一中心小学,福建福州,350017)
“双减”政策之下,学校要确保小学一、二年级不布置家庭书面作业,小学三至六年级书面作业平均完成时间不超过60分钟.60分钟是语数英三科作业时间,分给数学的恐怕只有20分钟左右,对五、六年级来说差不多4~5题.在题量精简的情况下,要达到利用课后练习巩固知识,如果依旧如从前,只是简单机械地采用市面上的试题,一方面时间不予许,另一方面学生容易产生枯燥感,效果不佳.想要事半功倍,就要求老师们能将已有题型进行改编,才能利用最少的题达到最佳的复习效果.笔者认为改编试题可以从以下方向入手.
1 指向认知难点,关注本质辨析
“双减”政策下,要求考试范围不能超出教学大纲.不超纲的情况下,难题依旧存在.难是在于这类题目更加注重考核孩子思考问题的本质,也就是我们常说的关注知识产生的过程.小学阶段的孩子思维还不够清晰,容易出现“重方法,轻理论”的错误.我们可以针对学生思考过程中的“薄弱点”,找准缺口,设计巧妙的试题来凸显学生的认知缺漏,帮助学生辨析易混淆的概念,提升思考的有序性,从而促进学生养成高品质的思维方式.
例1图书馆新购进一批图书,统计情况如下图,能比较准确表示购进各类图书占比情况的是
( )

A.

B.
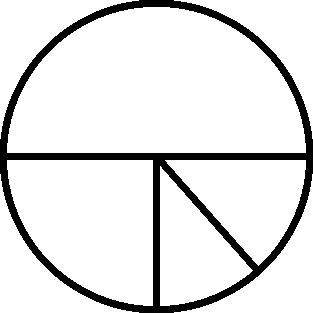
C.

D.

以“统计与概率”中扇形统计图为例:常见的题型多是计算各部分占整体的百分比,体现扇形统计图的特点.例1则侧重考察统计图知识的联系和应用.该题以条形统计图的方式,间接呈现各类图书数量情况,其中作文类和绘本类图书的具体数量无法得知.为了将条形统计图转换成扇形统计图,就需要学生运用以下能力:(1)从统计图中收集数据,估计作文类图书和绘本类图书的总量大概为100本,培养学生数感;(2)根据需要分析数据,从图书总数量判断出科技类图书占比50%,寓言类图书占比剩下的50%,培养学生数据分析观念和推理能力.
仅仅通过一道题,不仅联系新旧知识,还锻炼学生收集数据和处理数据的能力,更是帮助学生辨析统计图的应用,最终达到提升学生思维品质的目的.
2 指向思维支点,关注能力发展
数学教学的本质在于发展学生的数学能力.除了课堂教学,教师也可以通过设计试题提升学生的数学能力.题太易,学生“做之无味”;题太难,学生“望之生惧”.教师就需要找好平衡点,在知识点的思考点和难点找到支点,从而撬动学生的思维,达到发展学生数学能力的目的.
例2同一个钟面,分针和时针转动的速度之比
( )
A.12∶1 B.60∶1 C.1∶12 D.1∶60
以“数与代数”中比和比例为例:常见题多是计算比或比例,一般是能直接计算得到.本题虽然是基于生活中常见的“钟”作为背景,考查的却是“分针和时针转动的速度之比”这一不常见问题.学生大部分都认为分针转一圈是60分钟,时针转一圈是1小时,过于看重数字上的区别,而忽略单位的不同,从而选择B.本题借助比,充分关联“路程、时间和速度”的数学内部信息,速度比可以转换成单位时间内,分针和时针的路程比.一小时,分针转动60小格,时针转动5小格,所以分针和时针的速度比是12∶1.
为了提高学生参与思考问题的程度,设计试题时可以适当隐藏导向性,迫使学生主动思考,探究知识本质,做到让学生有路可循、有据可依,有条理地思考问题.从而激发其思考意识,有效提高学生的数学素养能力.
3 指向问题视点,关注过程体验
学生具有极强的个体差异性,他们数学水平、思维各异.如果我们设计出的试题具备开放和层次性的特点,就能将学生不同的思维水平一一展现.而开放性的试题也能给孩子的数学思维提供广阔的空间,带来不一样的过程体验.
例3将一张长80厘米,宽40厘米的长方形铁皮,通过切割和焊接,做成一个深为10厘米的无盖长方形铁盒(焊接处与铁皮的厚度不计),这个铁盒的容积会是多少立方厘米?请画出简要的设计图示.
以“图形与几何”中容积为例:常见题型多在于表面积、容积之间互相转换和计算.本题的解答方式不唯一(如下图所示),精髓是在于要求学生先“画出简要的设计图示”.借助图示的帮助,学生在脑海里想象出切割过程和所得长方体的形状.使学生锻炼空间想象能力,建立空间观念.

(方法一)

(方法二)
所谓条条大路通罗马,针对同一问题,却有不同的解答方法.关注结果的同时,更关注的是学生解决问题过程的体验,从而提升学生创新意识和创新能力,让不同的学生在数学上有不同的发展.
4 指向文化起点,关注生活应用
数学文化有着悠久的历史,因此数学习题的信息除了来自生活,也可以溯源我们的数学历史,渗透数学文化.指向文化起点的数学信息一般会间接呈现,学生需要发现、获取、辨识进而正确选择信息,才能解决问题,培养学生分析数学信息的能力,帮助建立数据分析观念,同时让数学文化回到我们的课堂.
课标中也曾指出:“为了考查学生从详细情境中获取信息的才能,可以设计阅读分析的问题”.这里的“阅读”指的是数学式的阅读,有的试题会借用“勾股定理”的背景,让学生进行数学式的阅读;有的试题背景不拘泥于数学文化,也可以源自生活,如来自“三坊七巷”的一段数学信息复杂的介绍(如下:例5),让学生能根据数学问题从繁琐的数学信息中进行选择.不论是溯源数学文化历史,还是源自身边情境,区别于语文阅读的数学式的阅读渗透数学知识,在数学知识中理解数学文化的数学观.
例4福州市台江区的上杭路和下杭路及其附近街区,俗称“双杭”,也就是“上下杭”.永德会馆坐落于福州下杭路张真君祖殿斜对面,是一座中国传统建筑风格与西方建筑元素相融合的近现代优秀建筑.坐南朝北,占地面积1 224平方米,东西宽36米,9柱8间排,其中正厅两侧厢房,东厢1间、西厢4间;进深7+2柱,长度34米.一、二层高度各4.5米,西式建筑元素居多.第三层歇山顶,层高5.5米,面积400多平方米,纯属清代古建筑.作为三层建筑的永德会馆高多少米?
小学数学课程标准指出,在设计试题时,应该关注并且表达课标设计思路中提出的十大核心词,要注重考查学生对数学本质的理解.我们改编试题,并不意味着出“偏题”“怪题”,而是设计少量但是能精准地把握课标要求的试题.这样才能更好地考察学生的学习成效,提升数学思维品质.同时还能体现出我们的教学成效,便于教师及时调整,提升教学质量,最终人人都能获得轻松并良好的数学教育.
