高中生空间能力现状调查研究
2022-11-15黄欣然
黄欣然
(南京师范大学教师教育学院,江苏南京,210023)
1 问题的提出
空间能力(spatial ability)在人类认知能力中占有重要地位,也被认为是人类智力结构的一个基本维度,是产生、提取、保持以及操作视觉空间信息的能力(Lohman,1996)[1].关于空间能力的研究,在心理学与教育学领域已有百多年的历史.Francis(1800)在他的实验调查中首次提出了心理表象这一概念.从此,研究人员开始把空间能力作为一般智力的重要组成部分加以研究,并采用不同的方法来检测其成分.近年来,心理学家和教育工作者越来越关注空间能力的研究,空间能力与人们日常生活息息相关,研究主要集中在空间能力的测量及培养等方面.在一项针对40万高中生的大型研究中,发现空间能力在科学、技术、工程和数学(STEM)领域中发挥重要作用[2].空间能力更高的学生在大学专业的选择甚至之后的职业规划都会更加倾向与STEM有关[3].同时,空间能力是一种重要的认知能力,它同样增加了成功解决应用问题的机会[4].由此可见,重视学生空间能力的培养对数学成就以及个人成长有着极其重要的意义.
更高层次的数学在本质上所需的多数思维是空间思维[5],培养学生运用空间思维认识事物一直是数学教学的重中之重.《义务教育数学课程标准(2022年版)》提到:“在数学课程中,应当注重发展学生的空间观念[6]”,《普通高中数学课程标准(2017年版)》指出:“通过高中数学课程的学习,学生能发展几何直观和空间想象能力[7]”.空间观念、几何直观、空间想象是空间能力内涵下不同层次水平的再现[8],自1963年正式提出数学三大能力,到现在倡导发展学生的数学核心素养,如何培养学生的空间能力始终是数学教育关注的话题.
2 研究意义
在学生自身素养方面,提升空间能力可以帮助学生形成良好的思维习惯,思想观念和思考方式,从而使学生能够运用恰当方法解决问题,促进各方面数学核心素养的发展;在学生身心发展方面,培养学生空间能力有利于人脑右半球的智力开发以及创造性思维发展,能极大培养学生的创新意识和创造力,综合强化学生整体素质;在课程目标与教学方面,空间观念与能力的养成是教育培养人的重中之重,学生的空间能力的培养应当贯穿于课堂之中,空间能力的调查研究为教师教学提供建议和指导,也有利于教学目标的落实.因此,通过调查学生空间能力的现状,分析学生在空间能力上的差异性,了解其在数学学习活动中的空间观念,以空间观念为基础提出发展学生空间能力的建议.
3 研究设计
3.1 概念界定
关于空间能力的详细定义,杨孟萍和石德澄(1990)指出,空间能力是一种认知图形,并运用图形在头脑中进行图形操作的能力,它的主要内容就是在解决任务的过程中运用图形表象,它的操作单位不是词,而是能表现客体的空间特征和关系的表象,如构成客体的各种因素的形状、大小、相互位置,以及客体的各种构成因素在平面上、三维空间上相对于特定位置的排列次序[9].李洪玉(1999)在归纳总结他人对空间能力的概念界定的基础上指出:空间认知能力是指人们对客体或空间图形(任意维度)在头脑中进行识别、编码、储存、表征、分解与组合和抽象与概括的能力.它主要包括空间观察能力、空间记忆能力、空间想象能力和空间思维能力等因素[10].目前为学术界所普遍认可的空间能力是指生成、保留、提取和转换视觉图像的能力[2].
空间能力维度如何划分至今一直尚未有明确的定论,不同的专家学者根据其研究的内容目标的差异对维度有不同的解释.Linn和Petersen(1985)将空间能力划分为空间知觉,心理旋转和空间想象三类因素[11].齐建林等人(2003)通过因素分析将空间能力划分为空间视觉化能力和空间定位能力,其中空间视觉化能力主要包括心理旋转,而空间定向能力主要包括对图形排列关系的理解,根据自身和其他物体定向的能力[12].李洪玉和林崇德(2005)通过考察中学生的空间认知能力,将空间能力分为图形分解与组合能力,数学关系形象化表达能力,心理旋转能力,空间意识能力,空间定向能力,图形特征记忆能力和图形特征抽象与概括能力等[13].周珍等人则将空间能力分为空间的心理折叠、心理展开以及心理旋转[14].本研究也采用周珍的分类方式.
3.2 研究内容
本研究的抽样对象为江苏省某四星级中学高二、高三年级的138名学生.测试卷采用Ekstrom等人1976年设计的两种经典空间能力测试题,该测试卷分为两个部分,分别是20个项目的心理折叠与展开测试,主要测试和评定学生视觉化的空间能力(图1).

图1 心理折叠与展开测试示意
另一个是包括20个项目的心理旋转测试,主要测试和评定空间关系的空间能力[15](图2).测试时间为15分钟,经过数据清理与筛选,剔除无效数据,最终获得有效数据134份.
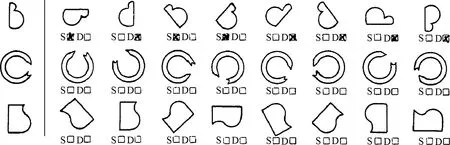
图2 心理旋转测试示意
3.3 研究方法
以空间的心理折叠与展开、心理旋转为两大维度测试.通过测试卷调查得出的数据用数据分析软件SPSS 25.0与办公软件Excel进行统计分析得出相关结论.该测试卷信度为0.842,难度为0.220,区分度为0.675.
4 研究结论
不同学生空间能力的差异较大,最小值与最大值之间的差值均大于10分,尤其是心理旋转能力差值达到16.87分,空间能力总分的差值更是达到了23.25分.

表1 空间能力测试统计分析
学生数学成绩与空间能力之间呈正相关性,相关系数为0.287,且在0.01的水平上显著相关.
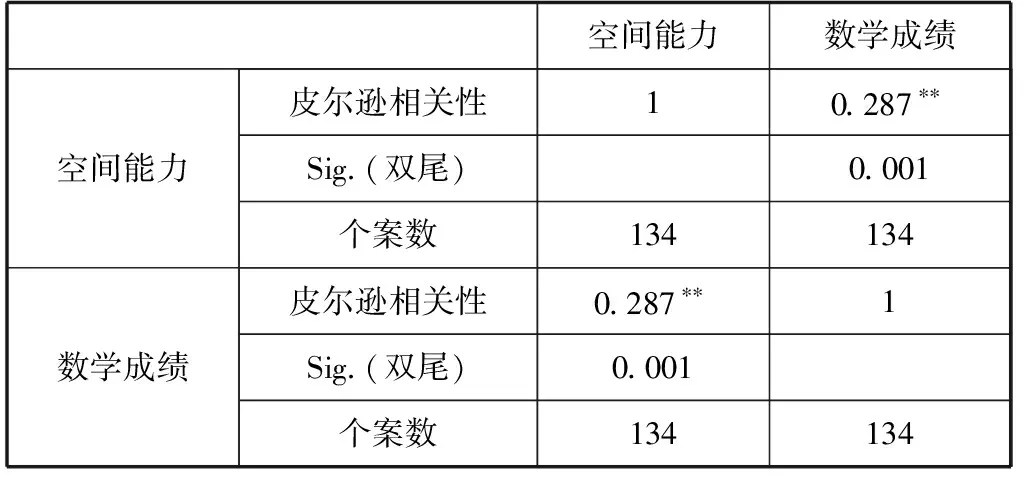
表2 空间能力与数学成绩的相关性
学生心理折叠与展开能力以及空间能力总分在学习优困生存在显著差异,心理旋转能力无显著差异.学习成绩优秀的学生空间能力强于学困生.
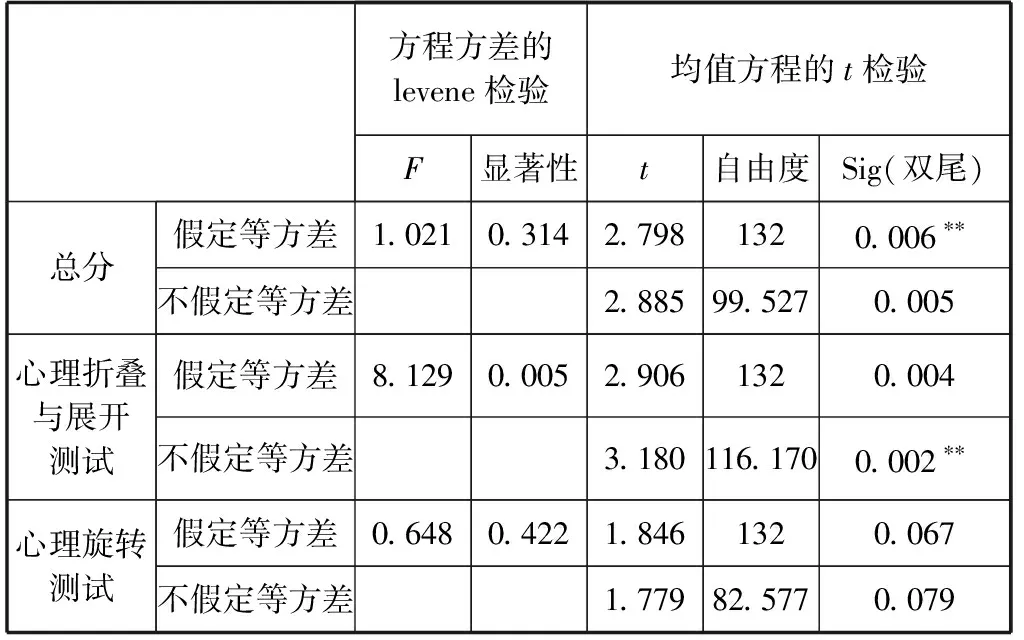
表3 学习优困生空间能力的差异性分析
学生心理折叠与展开、心理旋转与空间能力总分均未在性别上显示显著差异.
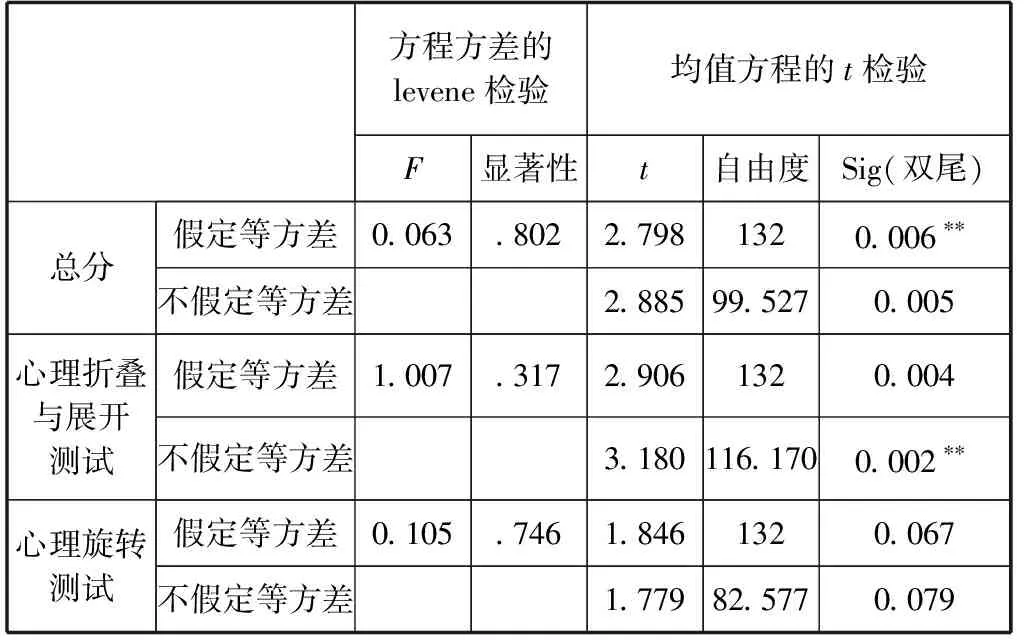
表4 学生性别与空间能力的差异性分析
学生心理折叠与展开能力以及空间能力总分在学生年级上存在显著差异,心理旋转能力无显著差异.高二学生的空间能力强于高三学生.
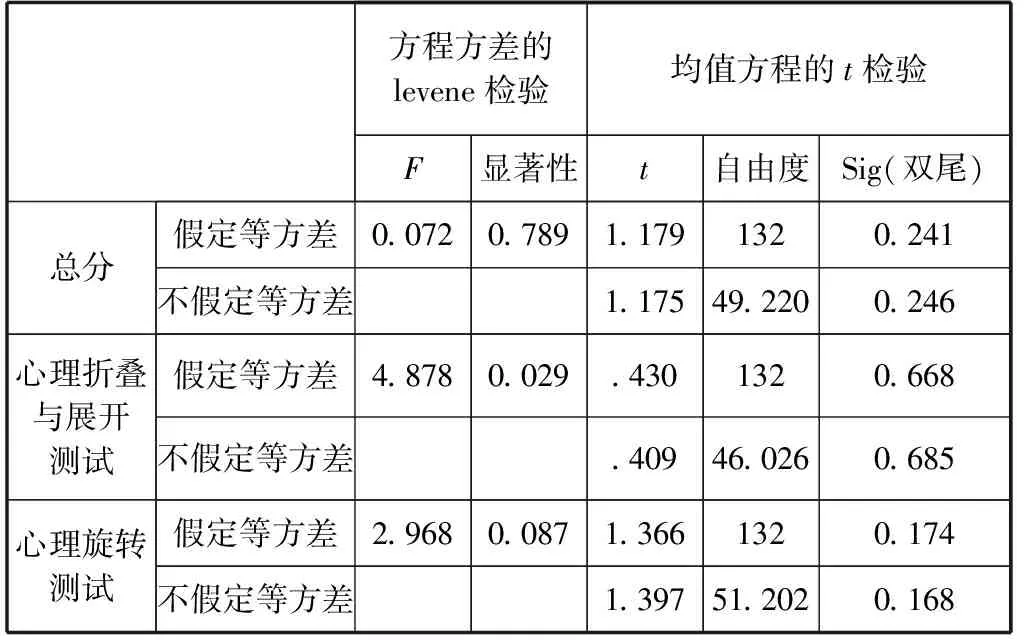
表5 学生年级与空间能力的差异性分析
5 讨论与小结
2022年4月新颁布的《义务教育数学课程标准》(以下简称“新课标”)中,明确了义务教育阶段的15大素养,其中“几何直观”与“空间观念”是小学与初中阶段的共有素养.同时,在《普通高中数学课程标准》中,空间能力也是核心素养的表征之一,空间能力的提升带来的将是学生整体素养的提升.
本研究将空间能力分成心理折叠与心理展开以及心理旋转两大维度,心理折叠与展开本质上是学生在头脑中对几何图形进行的二维与三维之间的维度转换,是学生空间能力的重要体现.测试中发现,学生在心理折叠任务中主要有两种解题策略.面对题目所给的二维纸张折叠图,少数学生倾向于利用某一点的位置,逐步还原该点在每一次展开后所在位置,再依次类推所有点的位置,从而进行判断;多数同学则是在头脑中想象出完全展开后纸张的形态,再根据初始点的位置确定展开后所有点的位置,从而得到答案.实际上,不论是哪种方式,都需要学生具备良好的二维与三维图形的空间转换能力.教师应当根据学生不同的思考策略在实际教学中引导学生构建空间立体图形,同时在立体几何的教学中,也需要注重策略的选择,从而构建起平面与立体,“数”与“形”之间的关系.
在心理旋转测试时,遇到复杂图形,如不规则图形中形成的角多于两个、图形有直有曲时,研究发现学生耗费的时间过多,这也是造成学生在心理旋转测试上分数不理想的原因.这也表明,学生对于较复杂图形的认识不到位,无法抓住图形旋转时的关键点,从而投入过多认知努力,造成心理焦虑[16],不仅造成时间的浪费,也会使学生更加无法在集中注意脑中形成旋转的视觉图像,陷入恶循环.
从研究结果不难发现,空间能力与数学成绩显著相关.提高学生的空间能力可以锻炼空间思维并强化空间观念,不仅会对立体几何、空间向量的问题解决产生帮助,更会在解决其他数形结合问题时提供思路.国外学者以儿童为研究对象考察了心理旋转能力与数学能力的关系,结果发现视觉空间工作记忆训练可以显著地提高儿童的心理旋转能力,进而提高其数学能力.对教师来说,在教学之外适当对学生进行空间能力的训练,譬如进行图形维度的转换训练,该训练主要是图形的空间性质、关系的内化过程,在此过程中学生的思维在二维与三维空间不断转换,空间想象力得到提升.此外,在课堂教学中,教师还可以适当运用丰富的教学技术手段直观形象地展示几何,譬如运用几何画板或GGB等辅助教学,通过动画与空间几何的呈现,从而让学生一目了然地体会到几何形态的变化过程,从而加深空间观念.
此外,本研究发现学生空间能力的发展并不具有相应的连续性,并未随学段的增加而得到提升,不符合以往研究得到学生的空间能力随年级或年龄的增长而提高的结论.在与任课教师交流后得知,一方面高三学生面临升学压力,学生大多关注于数据计算与如何解题,注重掌握解题思路方法的训练而非能力的培养;另一方面,立体几何知识属于必修二,高二学生刚刚接触过,一定程度上强化了学生的空间观念与空间能力.也提醒教师,学生常常容易出现“学了前面,忘了后面”的情形,在这种情况下,教师可以通过大单元整体教学的设计,形成知识与知识之间的有效联结的方法巩固;也可以通过螺旋式复习的方法,教学知识与其他已学单元进行串联,在教会学生解题的同时,在学生脑海中形成知识图块,从而加强空间能力的培养.
