让每一堂数学课都是一段愉悦的旅程
2022-11-15黄雪林
黄雪林
(吴江盛泽中学,江苏苏州,215000)
常常听到高三学生抱怨:“高考结束以后,我再也不学数学了!”可见孩子在高中数学学习的过程中感受到的只有痛苦.作为一名高中数学教师每每听到这样的抱怨都有深深的刺痛感,为什么原本生动有趣的数学学科在学生的眼里是如洪水猛兽一样的灾难形象?数学学科本该是和物理、化学、生物这些学科一样活泼、灵动有趣.然而现实中充斥着“唯解题”式的课堂教学,把数学这样一个天生丽质的美人给装扮成了一个令人害怕的怪兽,学生茫然地在数学的“题海”里浮沉,不知道从哪里来要往哪里去,这样的课堂谁又不恐惧呢?
如果每一堂数学课都是一段愉悦的旅程,在每一段旅程中教师都能够引领学生探究世界和思考世界,体悟到数学的魅力,从而快乐地学习数学,相信每一位学生都能够学好数学,自然在数学考试中也能够获取较好的成绩.然而什么样的课堂教学才能够实现获取心灵的愉悦呢?温暖的课堂氛围下,学生自由的思考世界、自如的探究世界本质、自然的生成数学概念、公理、定理,在课堂中获得心灵的愉悦.笔者就自己在构建高中数学现象教学课堂过程中的点滴做法与诸位分享,不足之处,敬请指正.
1 观察表象世界,感受数学源于生活
我们的数学课堂教学“希望能给学生带来愉悦感并喜欢上数学”.基于对现象探究的数学课堂教学,引领学生像数学家一样观察表象世界,探寻现象背后的数学本质,在数学学习过程中自然生成数学概念.这样的数学课堂教学能够帮助学生发现数学的美,促使学生自主地去探寻现象背后的数学本质.真正体悟到“兴趣是最好的老师”,在学习过程中哪怕遇到困难仍然愿意迎难而上,甚至能够做到再苦再累也心甘情愿.
我们的课堂教学总是花费太多的时间去思考课堂引入要靠什么去激发学生对数学概念、公理定理的兴趣.如果过于依赖数学以外的材料并不能有效地帮助学生获得成功的愉悦,我们应该引领学生去发现数学自身的美、自身的魅力.这样的课堂教学才能帮助学生真正领会数学的本质、真正学好数学、学到真正的数学.
以讲授2019人教A版教材必修二第八章“二面角”的概念为例,教材中以“开门”这样生活中最为常见的事情来理解二面角,“把门开大一些”是指哪个角大一些?来引导学生思考如何去剥离表象世界,探寻本质世界.门和墙面我们都可以抽象为平面来理解,都是规则的矩形,这是特殊的形状学生很快就能够理解并找到二面角,这个处理很好.但是对“二面角”概念的探究不能到这里就戛然止步,然后按部就班的给出来概念的表述、开始例题讲解、习题训练.二面角的概念此时还并没有在学生脑子里形成,所有的表述都还是老师自己的理解,我们要继续引领学生去探寻世界.
“开门”“打开书本”“打开笔记本电脑”这些都属于同一个情境,都属于矩形抽象为平面,三角形能不能抽象为平面?梯形能不能抽象为平面?不规则的平面图形,像一片叶子,随手扯的一张纸能不能抽象为一个平面?答案是肯定的,随手撕一张不规则的纸片,折成两个半平面能不能使得这两个半平面的二面角为30°、45°、°60°、90°?你如何能说明这个二面角是30°、45°、°60°、90°?
学生做了非常好的演示:我把三角板45°的两条边直直的插在两个半平面的交线处,就得到了两个半平面的二面角为45°.要想得到两个半平面的二面角为30°、°60°,也按照同样的方法去做就可以了.(如图1)
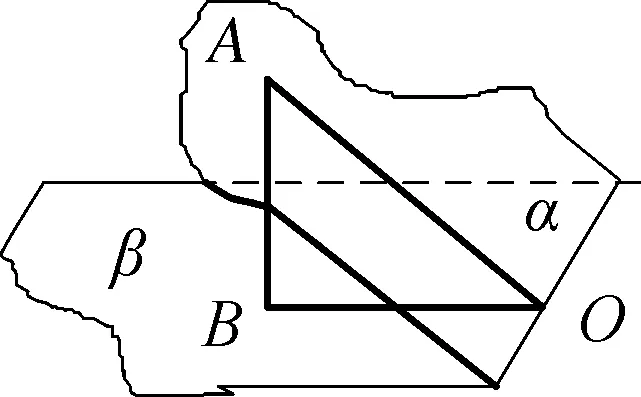
图1 “二面角”演示
师:直直的插在两个半平面的交线处,能不能用数学化的语言描述?
生:使得三角板ABO的两条边BO、AO都垂直于两个半平面的交线.

图2 “二面角”的平面角的求法
师:三角板ABO的两条边BO、AO都垂直于两个半平面的交线,和“开门”“打开书本”“打开笔记本电脑”使得两个半平面的二面角为45°有什么区别与联系吗?
生:要让“开门”“打开书本”“打开笔记本电脑”这样两个半平面的二面角为45°,也可以把三角板ABO的两条边BO、AO都垂直于两个半平面的交线.这个过程是一样的,没有区别.
师:如果没有三角板,比如我想得到这张不规则的纸片,折成两个半平面的二面角为15°?你们能得到吗?
生:那我可不能保证,但是我可以像插入三角板一样用线段画出这个角来求这两个半平面所成二面角.在两个半平面的交线上取一个点O,分别在两个半平面α、β内引垂线AO、BO都与两个半平面的交线垂直,∠AOB如果是15°这两个半平面所成二面角就是15°.
师:非常好,这就是两个半平面所成二面角平面角.这个不规则纸片折成的两个半平面可以代表任何情况下的两个半平面,所以在两个半平面的交线l上任取一个点O,分别在两个半平面α、β内引垂线AO、BO都与两个半平面的交线l垂直,∠AOB就是这两个半平面所成二面角的平面角.
观察表象世界的过程不应该浅尝辄止,我们的课堂教学不要舍不得花时间引领学生去探寻以现象背后的数学本质.一定要带领学生亲历从特殊到一般的探寻过程,真正做到对数学概念的理解.让每个学生都能真切感受到数学是源于生活的学科.
就像理解“夏天”不是在池塘边触摸一下荷叶就是夏天,我们还要感受蛙叫蝉鸣、烈日清风甚至蚊叮虫咬才能够认识真实的“夏天”.高中数学的课堂教学也是这样,我们不要害怕学生探究不到理想的答案,重要的是体悟世界的过程.
2 思考本质世界,亲历数学公理定理的发现
数学定理的证明过程蕴含着数学家们当初面对这一数学现象时的数学思想方法.数学课堂教学过程中我们要结合现象还原数学史,引领学生了解数学定理的来龙去脉以促进学生思维发展,感悟数学家们的探索和创新精神.数学定理是数学教学的重要内容,数学定理的教学应该立足于揭示定理本身的数学内涵、分析定理丰富的文化价值.尊重逻辑推理和定理的演变进程体悟数学推理的理性美、数学语言的简洁美.
2019人教A版教材必修二第六章“正弦定理”是解斜三角形的重要工具之一,将初中所学的直角三角形的边角关系延伸到斜三角形.教材中正弦定理的证明采用的“向量方法”是基于1748年数学家欧拉在其著作《无穷分析引论》中给出利用“三角形的高为辅助线”的结合第六章平面向量挖掘的证明方法,在证明的过程中能够帮助学生很好地感知平面向量是沟通几何与代数的工具性功能.


图3 欧拉的证明
美国数学教育家M.克莱因(M.Kline, 1908—1992)认为:“历史发展的顺序可以为数学教学指明方向,我们没有必要完完全全仿照知识的历史发展,但是如果大数学家们在提出某些概念或者定理时遇到困难,我们学生也是会遇到的.教师在建构性地教授数学时,运用发生原理是极为有益的.”
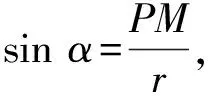
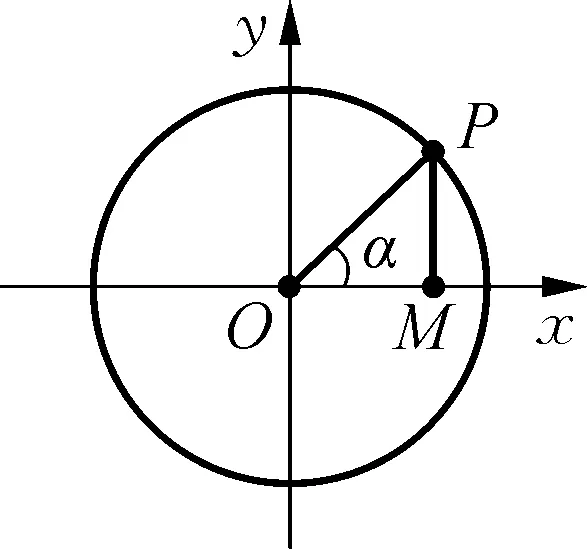
图4 正弦的定义
基于正弦的定义源于圆,十八世纪前,数学家们思考正弦定理的证明基本上都是通过构造圆的弦来实现的.如图5,作△ABC的外接圆O,从外接圆的外心O向AB、BC和CA作垂线,垂足分别为D、E和F.
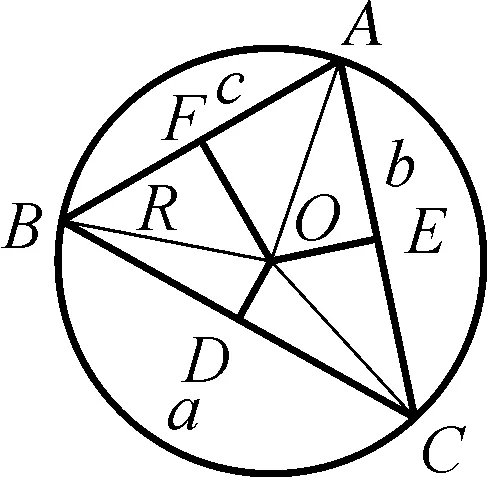
图5 韦达的证明
则∠BAC=∠BOD,∠ABC=∠AOE,∠ACB=∠AOF.
这是法国数学家韦达(F.Viete,1540—1603)在著作《数学法则》中证明了正弦定理的方法,与教材中的“向量证明法”和欧拉的“三角形高的证明方法”比较,这个证明方法完整的呈现出了正弦定理的几何意义.为今后在立体几何中理解外接球等相关问题做了较好的思维铺垫.
在教学过程中,教师可以请同学们思考能够思考出其他的证明方法?下面展示两种同学们思考的证明方法:
方法1:向量投影法——基于“欧拉的证明”结合向量的思考
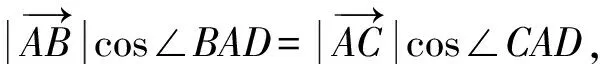

图6 向量投影证明

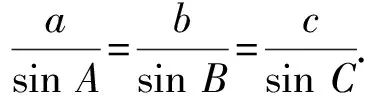
点评:巧妙地利用了向量投影的概念,可以说是欧拉证明方法的向量版本.与教材中提供的向量法证明比较,更为充分地体现了数学的简洁美!较好地体现了孩子们学以致用的学习精神!
方法2:三角函数定义法


图7 三角函数定义证明

点评:这是一个非常妙的证明!二次建系巧妙地运用了正弦的定义,真正认识到坐标系是沟通代数和几何的重要桥梁!为今后学习解析几何打下了思维基础,时代的进步赋予了当代中学生可以轻松地获取更多的知识,然而人类认识世界的方法自古以来几乎是一致的.只有不断地探索和思考,才能够迸发出创新思维的火花!
3 应用真实世界,做数学题的设计者
例题和习题是课堂教学的重要组成部分,是实现数学概念和数学定理等重要知识结构化、系统化的重要素材,也是学生感悟数学魅力的重要.“快乐的数学课堂教学”同样需要例题和习题,教材中的例题和习题都是编撰者结合学生的认知规律和思维发展规律精心设计的.在课堂教学中我们要用好这些例题和习题,同时也可以大胆地让学生自己设计例题和习题.
在课堂教学的过程中有意识地鼓励学生尝试扮演命题人的角色,从命题人的视角改编、创作出全新的数学问题,有利于培养学生思考如何将数学概念、公理定理应用于真实的世界.有利于问题意识的萌发、创新思维的促进、合作能力的提升等各方面能力的培养.

师:要判断两个函数是否为同一函数应该从哪些方面考虑?
生:定义域、值域和解析式要一致.
师:你能否列举两个函数定义域和值域一致,但是解析式不同的函数?
生1:y=2x和y=2x+1,所有的一次函数定义域和值域都一致,所有的反比例函数定义域和值域也一致,所有的二次函数定义域和值域也一致.
师:你能否列举两个函数解析式和值域一致,但是定义域不同的函数?
生2:y=1和y=x0?(表现略显迟疑,不是很肯定.)

生4:y=1和y=x0是值域和解析式相同,定义域不同的函数.满足值域和解析式相同,定义域不同的函数有很多,比如二次函数y=x2,x∈(-∞,0)和y=x2,x∈(0,+∞);y=2x2+1,x∈{1,2}和y=2x2+1,x∈{-2,-1,2}……这样的例子有很多.
师:你能否列举两个函数定义域和解析式一致,但是值域不同的函数?
生:如果两个函数定义域和解析式都一致,值域不会不同,就是同一个函数了.
师:所以要判断两个函数是否为同一函数,我们只需要从两个函数的定义域和解析式去判断.你能不能命制一道关于函数三要素这个知识点的考察的例题并进行讲解?
课堂上收获了很多关于判断函数是否为同一函数的习题,有一位同学命制了这样一道题:已知函数解析式为y=5-x2,值域为{1,4}的函数一共有多少个?讲解得也非常细致,获得了所有同学的掌声.这道题较好的引发了学生的思考,也从模仿走向了创新!在命制习题的过程中,每个学生都跃跃欲试,命制一道习题就如同在数学的版图中攻城掠地、开疆拓土般的快乐.切换为习题设计者帮助学生建立起自己是数学题的设计师掌控人的愉悦感,取代了一直是练习题的操控者的被奴役的痛苦.
4 结束语
基于现实世界的高中数学课堂教学坚持帮助学生观察以现象呈现的表象世界,分析思考本质世界的数学属性,应用本质世界的数学属性去解决真实世界的实际问题.当学生亲眼看见数学知识是如何从他们身边活泼的世界中产生并解决他们的困惑,自然就能够体会到数学的魅力,从而激发对数学学习的兴趣.深度思考和深度学习帮助他们建立起对数学学科的热爱,实现“愿意终生与数学交朋友”的目标.
在平时的教研活动中,我们要潜心研读教材,结合数学史的背景回溯数学概念、定理的源流,在课堂教学中引领学生亲历概念、定理的演变进程,帮助学生感同身受数学家们的困惑、思考和问题解决带来的快乐!尽可能地给学生机会命制习题,学会站在命题者的视角审视习题,尝试改编例题、创作习题享受数学的探索精神.将自主思考、合作探究的习惯融入到日常教学活动中.我们的数学课堂也可以像物理、化学课一样做拥有数学实验课,在实验探究中体悟数学家发现数学公理定理的探索之旅……数学这个天生丽质的美人,我们要引领学生从不同的维度去感受她的美!
