基于“三教”理念的“余弦定理”教学探索
2022-11-15陆娅君陈明万
陆娅君,靳 朋,陈明万
(贵州师范大学数学科学学院,贵州贵阳,550025)
贵州师范大学吕传汉教授于2014年提出教思考、教体验、教表达(以下简称“三教”)的教育理念,旨在引领课堂教学,培育学生的核心素养.主张:教思考,重在培养学生的数学思维;教体验,重在增进学生的数学感悟;教表达,重在强化学生的数学交流.数学教学要重在“教思考、教体验、教表达”,既是回应教育哲学对人成长的关切,又是回答核心素养如何走进课堂的疑问[1].在数学课堂教学中如何使“三教”理念落地,成为当前教学实践中亟待解决的问题.因此,本文根据“三教”理念分析“余弦定理”的教学,谈谈如何将“三教”理念贯穿于课堂教学中,进而培养学生的核心素养.
1 “三教”理念概述
“教思考”,主要是指学生在数学活动中从已有的关系或知识出发,通过数学思维活动,在教师的引导下发现和提出问题,寻求解决问题的思路,通过推理运算得到新的数学知识,领悟数学思想方法.
“教体验”,是指教师通过创设情境搭建起学生体验的平台,在数学活动中引导学生观察和分析、抽象和概括,使学生进一步获得数学学习、问题解决的过程性体验,累积从具体到抽象的经验.
“教表达”是指既包括提高学生的口头表达能力,也包括提高学生的书面表达能力,对于数学教学而言,主要是指培养学生用数学语言来讨论数学、表达数学问题、表达数学结论的能力[2].
2 “三教”理念对“余弦定理”的教学启示
2.1 创设情境,直观感悟
某隧道施工队为了开凿一条山地隧道,需要测算隧道通过这座山的长度.如图1,工程技术人员先在地面上选一适当位置A,量出A到山脚B、C的距离,分别是AC=5 km,AB=8 km,再利用经纬仪(测角仪)测出A对山脚BC的张角,∠BAC=60°,如何求出山脚的长度BC?
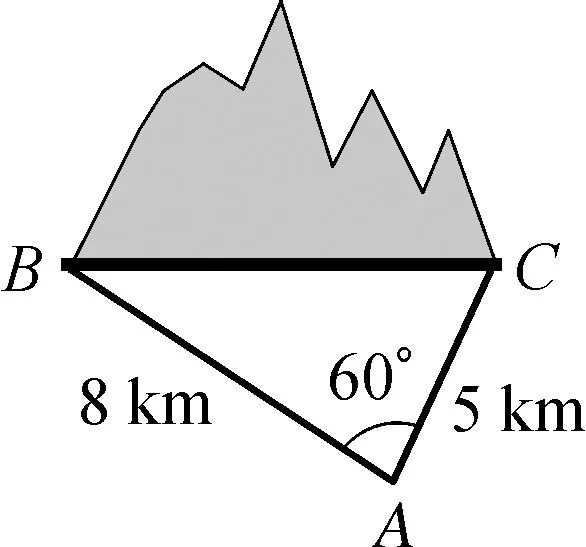
图1
问题1:上述实际问题可以数学化为什么问题?
问题2:已知三角形的两边及其夹角,能唯一确定第三边吗?
问题3:之前学习的正弦定理可以解决这个问题吗?为什么?
设计意图:学生能直观感悟出此隧道问题其实是三角形问题,进一步抽象出“三角形”模型,引导学生分析三角形中边、角之间的关系,学生经历观察、分析、抽象的过程,知道利用正弦定理无法解决此问题,从而寻求新的方式.在这个过程中,培养学生用数学的眼光发现与提出问题的能力.
2.2 问题驱动,探索新知
2.2.1 以问促思,推导定理
问题4:已知△ABC两边a、b及其夹角∠C,求第三边c.
(1)如图2,当∠C=90°时,求第三边c.
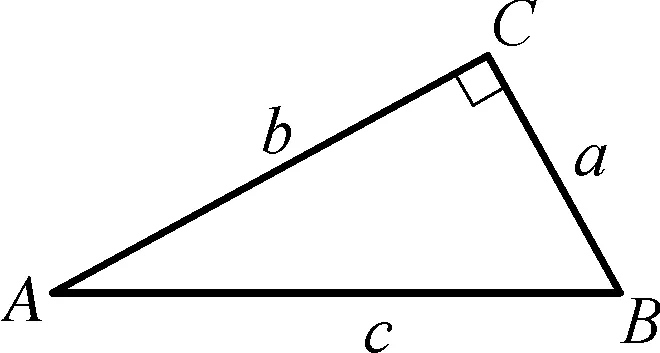
图2
生:用勾股定理,即c2=a2+b2.
(2)一般地,已知两边a、b及其夹角∠C,如何表示c2?
追问1:回顾之前探究正弦定理的经验,同学们有没有想到什么探究工具?可以用什么方法沟通三角形边与角之间的关系?能用同样的方法来探究吗?
追问2:如图3所示,已知两边a、b及其夹角∠C,如何用向量法表示第三边的平方?

图3
师:第三条边所对应的向量与已知的两条边所对应的向量具有怎样的关系?
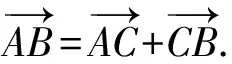
师:此时,如何求第三条边的平方?
生:两边平方.
师:边的平方也就是向量模的平方,即向量的平方.请同学们动笔计算,两边平方之后会得到怎样的结论?
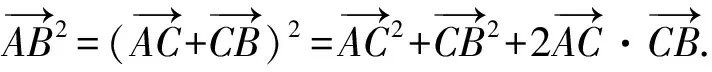
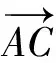
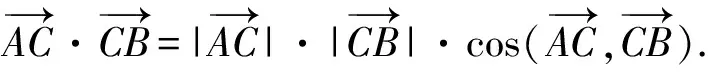
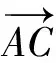
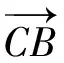
师:同学们还有不同的想法吗?
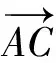
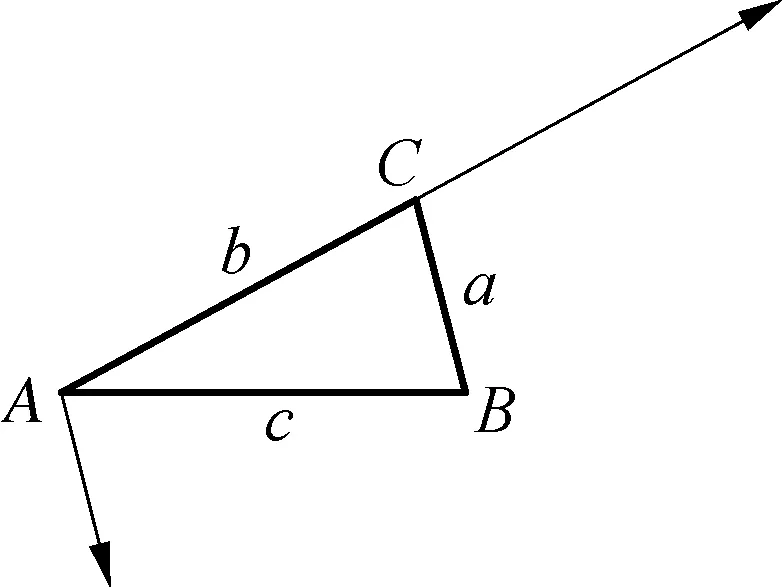
图4
生:互补.
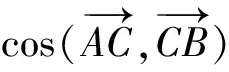
在教师的引导下,学生得出:c2=a2+b2-2abcos∠C.
问题5:已知两边b、c及其夹角∠A,第三边a与它们之间的关系?
a2=b2+c2-2bccos∠A.
问题6:已知两边a、c及其夹角∠B,第三边b与它们之间的关系?
b2=a2+c2-2accos∠B.
余弦定理:三角形任意一边的平方,等于其他两边的平方和减去这两边与它们夹角余弦的积的2倍.
设计意图:在探究三角形三边的数量关系时,以层层递进的问题引导学生思考,经历由特殊的直角三角形到锐角三角形的探究过程.首先探究余弦定理的难点在于运用向量法,在学生“愤悱”时,以追问1引导学生深入思考怎么沟通三角形边与角之间的关系,此时“类比”的思想根植于学生心中,逐步教会学生用数学的思维去思考.通过向量法沟通了三角形的边与角之间的关系,再通过代数运算得到等式:c2=a2+b2-2abcos∠C,通过观察、分析、归纳与概括,最终推导出了余弦定理.
2.2.2 以问促思,明确几何意义
问题7:能否从形的角度解释余弦定理的意义?
情形1:直角三角形中余弦定理的几何意义是什么?当∠C=90°时,余弦定理c2=a2+b2-2abcos∠C变成了什么形式?
生:勾股定理,即c2=a2+b2.
师:也就是说,勾股定理是余弦定理的一种特殊情形,那么勾股定理的几何解释又是什么呢?在初中阶段是如何来证明勾股定理的?
生:以直角三角形的三边为边长向外做出了三个正方形,以c为边长的正方形的面积等于以a为边长的正方形的面积与以b为边长的正方形的面积之和,如图5所示.
情形2:其它三角形中余弦定理的几何意义是什么?(以锐角三角形为例)
问题8:余弦定理c2=a2+b2-2abcos∠C,其中c2表示以c为边长的正方形的面积,a2、b2分别表示另外两个正方形的面积(如图6所示),那2abcos∠C表示的是哪两块图形的面积?
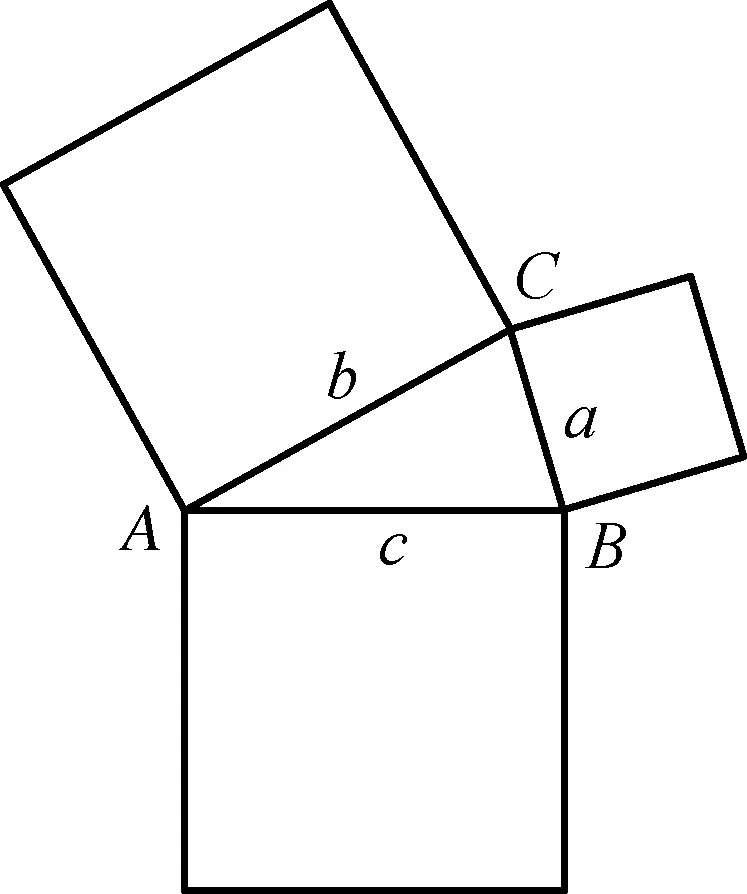
图6
追问1:abcos∠C可以表示为a·bcos∠C,也可以表示为b·acos∠C,那么bcos∠C、acos∠C分别表示什么?
追问2:过点A作BC边的垂线,垂足为E,bcos∠C表示的是什么?a又表示正方形的边长,此时a·bcos∠C表示的是什么?
追问3:类比刚才的作法,应该怎样作辅助线?acos∠C表示的是什么?b又表示正方形的边长,此时b·acos∠C表示的是什么?
如图7所示,锐角三角形中余弦定理的几何意义是:以c为边长的正方形的面积等于另外两个正方形的面积之和再减去两个矩形的面积(阴影部分),即正方形①的面积等于矩形②的面积与矩形③的面积之和.

图7
思考:对于钝角三角形而言,余弦定理的几何意义又是什么?
设计意图:为探究余弦定理的几何意义,从最简单的直角三角形入手,引导学生回顾初中阶段所学习的勾股定理的几何意义,并按照此思路进行类似的探究,渗透了从特殊到一般、类比的数学思想方法,逐步教会学生用数学的思维思考问题.将问题8分解为3个追问,以递进式问题启发思考,沟通数形之间的思维桥梁;追问1,通过对式子的适当变形,引导学生从不同的角度思考abcos∠C表示的是什么;追问2和追问3突破了如何用代数表示相应的图形,引导学生作辅助线、找关系,经历由数到形、再到数的推理过程.最后设置了思考环节,启发学生用类似的方法作进一步的探究,将分散的知识碎片整合联系起来,进而达到思维上质的飞跃.
2.3 总结升华,形成图式
2.3.1 回归情境,应用定理
问题9:情境中的隧道问题能抽象出怎样的数学模型?
问题10:如何应用余弦定理解决情境中的隧道问题?
问题11:已知条件有哪些,要求的是什么,如何用数学语言来表述?
问题12:观察一下余弦定理的这三个等式,请大家对这三个等式作一个变形,每个角的余弦值应该如何来表示?
问题13:变形后得到的公式可以解决什么样的问题?
设计意图:回归到实际问题中,引导学生经历应用余弦定理解决生活问题的过程,总结出解决问题的一般步骤:首先将情境问题抽象为数学问题,进而提炼出数学模型,再转化到三角形中进行研究,培养学生数学建模的素养;其次是分析清楚已知条件、要求解的问题,进而确定解题方案,即已知三角形的两边及其夹角,求第三边,需要列方程求解;最后设BC的长为x,根据余弦定理的等量关系列方程,进而求解出x的值.学生经历“抽象模型——表达模型——求解模型”的过程,培养学生的模型观念意识,提升学生用数学的语言表达问题的素养.
2.3.2 回顾整合,形成结构
问题14:通过本节课的学习,你收获了什么?
追问1:在推导余弦定理以及探究其几何意义的过程中,你认识到了哪些数学思想方法?
追问2:本节课是如何来探究的?
追问3:在探究的过程中,你联想到了哪些知识点?
设计意图:回顾整堂课所学,从中萃取精华,进而形成知识的整体结构和解决问题的一般思路,帮助学生对知识进行巩固与反思,提升学生用数学的语言表达问题的能力.
3 对教学设计的反思
以上关于余弦定理的教学探究,经历“创设情境、直观感悟;问题驱动、探索新知;总结升华,形成图式”三大环节,分别以实际问题为切入点、问题启发为着力点、形成图式为落脚点,每一环节都不同程度地体现了“三教”的教育理念,有利于学生理解数学本质、领悟数学思想方法以及发展核心素养.
3.1 以实际问题为切入点
在余弦定理教学中,以生活问题为切入点启发学生去观察,进而抽象出“三角形”模型,旨在让学生理解数学来源于生活,培养学生的数学应用意识;以数学的眼光抽象出三角形中边、角间的关系,引导学生寻求新的方式解决此问题,让学生明白学习余弦定理的必要性,激发学生探究问题的兴趣.
3.2 以问题启发为着力点
以递进式问题引领学生逐步深入探究,使学生的思维以螺旋上升式发展.在推导余弦定理以及探究其几何意义的过程中,都是从特殊的直角三角形入手,分别以一个大问题为核心,再逐步分解为递进式的问题串,满足学生的最近发展区,激发学生对锐角三角形中边、角关系以及余弦定理的几何意义等问题深度思考,在无形中渗透了从特殊到一般、数形结合的思想方法.这种递进式的问题串有助于学生推理能力的培养,启迪学生的思维,促进学生用数学的思维思考问题.
3.3 以形成图式为落脚点
在定理应用环节,不能仅停留在表层地解决问题上,应该学会归纳、表达建模步骤,形成知识的综合结构.在应用余弦定理解决问题之后,不仅要让学生学懂,还要融会贯通,只有对建模的思想和方法进行综合提炼,才能在下次运用时准确定位数学知识、方法和思想,培养学生的数学应用意识与数学建模的素养.
