见微知著:微专题教学的实践与思考
2022-11-15陈敏婕
陈敏婕
(南京师范大学附属中学邺城路初级中学,江苏南京,210019)
微专题教学是非常重要的一种教学形式,它立足教材又高于教材,教学设计灵活.其核心点在于“专”,落脚点在于“思”.指向学生对数学思想的抽象和应用,优化学生的数学思维,从而提高学生对于经验与方法的运用和迁移的能力,提升数学素养.下面以“函数图象视角下的方程、不等式”微专题教学设计为例,对此进行阐述.
1 教学目标与载体选取
1.1 教学目标
(1)知道函数与方程(组)、不等式(组)的关系.
(2)会用函数的图象,求相应方程(组)、不等式的近似解.
(3)通过两个函数图象解方程(组)的探索活动,感受函数与方程的辩证统一,感受函数图象与方程(组)、不等式的内在联系,体验知识的内在统一性与融合,感受数学在数学内部的应用是推动数学自身发展的动力之一.
1.2 载体选取
一次函数是学生最先接触的一类函数,也是最为熟悉的,它的图象呈直线样态.从一次函数的图象作为切入口,并且贯穿课堂始终,让学生充分感受数形结合思想.
通过问题串,串联各环节的教学组织,给予学生充分的时间和空间、思考与表达、总结与归纳,升华认知,感受三者内在的和谐与统一性.
2 教学过程
2.1 情境创设

图1
问题1:说说你对y=-x+3的认识.
设计意图:引导学生从两个不同的角度看同一个表达式,如果看成变量,它就是一次函数;如果看成未知数,它就是二元一次方程.
师生活动:
生:这是一个一次函数,y随x的增大而减小.
生:把-x移项到左边,可以看成是二元一次方程.
师:两位同学站在不同的角度,都对这个表达式就行了阐述.这里的x、y,如果看成变量,它就是一次函数;如果看成未知数,它就是二元一次方程.请同学们画出函数图象.
2.2 探索活动
问题2:一次函数y=-x+3图象上点的坐标与二元一次方程x+y-3=0的解有什么关系?
设计意图:引导学生发现一次函数与二元一次方程的内在联系,即一次函数图象上点的坐标就是二元一次方程的解;以二元一次方程的解为坐标的点都在一次函数的图象上.
师生活动:
师:你描的是哪些点?
生:(0,3),(3,0).
师:一次函数图象上点的坐标与二元一次方程的解有什么关系?
生:一次函数图象上点的坐标就是二元一次方程的解;以二元一次方程的解为坐标的点都在一次函数的图象上.
问题3:一次函数与一元一次方程有什么关系?
设计意图:引导学生发现一次函数与一元一次方程的内在联系,即当其中一个变量的值确定时,可以由相应的一元一次方程确定另一个变量的值.
师生活动:
师:再描一个点,已知它的横坐标是4,你是如何确定它的纵坐标的?
生:直接看图象,纵坐标是-1.
师:很好,同学们还有不同的方法吗?
生:代入函数表达式y=-x+3求解,y=-1.
师:刚才通过两种方式都得到了这个点的纵坐标.反过来,再找一个点,已知它的纵坐标是2,你又能得到什么?
生:这个点的横坐标是1,可以看图,或者代入函数表达式求.
师:当一次函数表达式中一个变量x或y确定时,它就变成了?
生:一元一次方程.
师:你觉得一次函数与一元一次方程有什么关系?
生:一次函数的表达式,当其中一个变量的值确定时,可以由相应的一元一次方程确定另一个变量的值.
问题4:一次函数与一元一次不等式有什么关系?
设计意图:引导学生发现一次函数与一元一次不等式的内在联系,即当其中一个变量的取值范围确定时,可以由相应的一元一次不等式确定另一个变量的取值范围.
师生活动:
师:一次函数除了与方程有着密切联系,从图象中你还能读出不等关系吗?
生:当y>0时,x<3.
师:你是怎么识图的,能分享下经验吗?
生:当y>0时,只要看图象上x轴上方的部分,此时对应的x<3.
师:类似的,请同学们尝试写出三个不同的不等关系.

图2
师:除了读图,你还有不同的方法得到“当y>0时,x<3”吗?
生:可以直接回看一次函数表达式当y>0时,也就是-x+3>0,解这个不等式.
师:你能说说一次函数与一元一次不等式有什么关系?
生:一次函数的表达式,当其中一个变量的取值范围确定时,可以由相应的一元一次不等式确定另一个变量的取值范围.
问题5:在原坐标系中再画一个函数y=2x的图象,结合刚刚的研究内容,你能提出一个问题吗?
追问1:如何求交点的坐标?
追问2:求关于x的不等式-x+3>2x的解集.
设计意图:引导学生发现两个一次函数图象的交点坐标,就是相应二元一次方程组的解.两个函数图象联系起来看,亦能看出不等关系.
师生活动:
师:如何求交点的坐标?
生:直接看图象,交点的坐标是(1,2).
师:你借助于图象的直观性,有同学利用不同的方式得到的吗?
生:通过联立两个函数表达式,解方程组.
师:大家通过两种方式得到了这个交点坐标,由此你有什么发现?
生:两个一次函数图象的交点,就是相应的二元一次方程组的解.
师:还有同学有不同的问题提出吗?
生:求等式-x+3>2x的解集.
生:我有两种方法,第一种直接求解不等式,第二种从图象上看,要满足y1>y2,也就是看图象上交点左边的部分,此时的x<1.
师:通过上面两个问题的研究,你有什么发现?
生:二元一次方程组和一元一次不等式,还可以借助于一次函数的图象直接读出结果.
2.3 拓展延伸
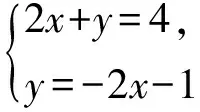
设计意图:引导学生从形的角度发现,两个一次函数图象平行时没有交点,相应的方程组无解.
师生活动:
生:方程组无解,两个函数的图象平行,没有交点,因为它们的k值是一样的.
问题7:求关于x的不等式-x+3>x2+1的解集.
设计意图:引导学生从多角度观察式子,提炼多种解法和思考路径.
师生活动:
师:你有哪些方法解决呢?
生1:画一次函数y=-x+3和二次函数y=x2+1的图象,从图象上看出解集.
生2:把这个不等式移项,整理得x2+x-2<0,画二次函数y=x2+x-2的图象,在x轴下方的图象部分对应x的值就是这个不等式的解集.
师:这个不等式,你想怎么命名?
生:一元二次不等式.
师:关于一元二次不等式,你还联想到什么?你有新的解法吗?

图3
生:我想到了一元二次方程,可以对式子x2+x-2因式分解得(x-1)(x+2),也就是(x-1)(x+2)<0,再根据异号两数相乘得负,得到这两个因式异号,分类讨论求解.
2.4 小结思考
问题8:通过今天的学习与研究,你对函数、方程、不等式有哪些新的认识?
追问:你还有新的问题提出吗?
设计意图:引导学生从整体上归纳、概括“函数、方程、不等式”的内在关联,进一步体会到通过“读图”常常可以为解决有关方程、不等式的问题提供方便;函数的图象直观,便于从“形”的特征解决方程、不等式的问题;“函数”是函数、方程、不等式三者关系中的主干这些深刻思想.
师生活动:
力争给学生充分的时间和空间,思考与表达,再整合归纳、提炼升华.
3 几点思考
3.1 主题遴选的整体意识
微专题的关键就是要选择有代表性的研究主题,聚焦于一些核心素材,确立合适的教学目标,通过设计有针对性的系列活动,从整体上看待知识之间的内在联系,旨在解决课堂教学中的一些典型问题.本专题正是基于以上考虑,抓住函数、方程、不等式三者之间一脉相承的关系,揭示知识的内在结构体系,实现其整体性和统一性.在教学过程中,突出了方法主线,不断地通过“数”与“形”的双向结合,让学生切身感受“数形结合”思想,以及图象解法的直观性、代数解法的精准性.正如华罗庚先生所言:“数缺形时少直观,形缺数时难入微”,本专题在“数”与“形”方面的整体处理意识,有效地促进了学生对知识方法的融会贯通.
3.2 问题设计的结构连贯
课堂顺利展开的有效纽带是问题,问题驱动的动力在于良好的问题结构,即环环相扣的结构性问题才能有效驱动课堂活动,诚如波利亚所指出的“良好组织的问题能使所提供的素材容易用上”.本微专题正是以8个结构性问题为驱动,由浅入深,逐步递进,体现了思维的连贯性与发展性.在问题的展开过程中,注意课堂中的充分“留白”,给予学生充足的思考时间与空间,启发学生从整体上看待知识间的内在联系,感受和谐统一的本质特征.其中问题1由函数引入,问题2~4分别将函数与方程以及不等式的关系串联起来,问题5通过再次引入一个函数图象,启发学生结合前面的研究经验,自主提出问题,问题6~8则是在内容拓展及深度思考上再加引导.
3.3 思考延展的深度取向
教学生学会思考应成为课堂教学的不懈追求,将知识的构建、方法的形成、能力的发展在学生深度思考的场域内自动生成.陈省身先生曾言:“数学是自己思考的产物.”学生思维素养的提升,主要依靠教师启迪、引导,激起学生自主探究的意识,而后自己及时反思、监控的思考行为.本专题正是基于以上的思考,确立了“教学生学会思考”的教学宗旨,着力为学生搭建深度思考的平台,帮助学生形成系统的知识和一般的数学研究方法.例如在核心问题的追问中,以及一些需要学生反思提问的活动环节中,都有效地激起了学生深度思考的兴致.
毋庸讳言,微专题的教学设计不同于新授课,新授课涵盖的知识点或涉及的思想方法可能并不系统,而微专题恰好可以弥补这方面的缺憾,从整体上把握核心知识及重要方法,起到“见微知著”之效.本文的探索只是个人教学实践中的“拙见”,后续尚有诸多问题有待探讨和完善.
