非规则V形表面织构化机械端面密封性能研究

赵文静，屠治荣，孟祥铠，江锦波，彭旭东

（浙江工业大学机械工程学院，浙江 杭州 310023）

引 言

密封端面织构化是一种有效提高机械密封摩擦学性能和密封性能的重要途径，它不仅有利于提高液膜刚度与承载能力，还能起到减磨、降低泄漏率和温升等的作用。密封端面表面织构的轮廓形状是提升织构性能的重要因素[1]。在织构轮廓形状的早期设计阶段，国内外学者主要关注于对比圆形、椭圆形、三角形等规则形状的摩擦学特性和密封性能。Etsion 等[2]采用数值模拟方法对球缺型面微孔织构的摩擦学性能进行了分析，但未考虑织构形状的多样性。Siripuram 等[3]对比分析了方形、菱形、圆形、六角形和三角形微凹坑织构和微凸体织构，发现凹凸体织构的截面尺寸对摩擦因数和泄漏率的影响较为显著；截面形状对摩擦因数影响较小，对泄漏率影响较大，且三角形微凸体的泄漏率最小，方形微凸体的泄漏率最大。彭旭东等[4]以最大液膜刚度为优化目标，获得了具有最优几何参数的矩形面、椭圆面、球缺面和抛物面，并指出矩形面微孔拥有最佳的综合性能。随后，又对比研究了圆形、正方形、正六边形、三角形的微凹坑织构和微凸体织构，发现同工况下微凹坑织构的密封性能优于微凸体织构，且三角形织构在高速低载工况下具有良好的摩擦学特性[5]。Yu等[6]对比分析了单个圆形、椭圆形与三角形织构在不同滑动方向上的摩擦学性能，发现微孔织构的方向性对承载能力具有重要的影响作用。Qiu 等[7]研究了不同织构对机械密封性能的影响，结果表明相比于圆形织构、长轴沿径向方向的椭圆形织构，长轴沿圆周方向的椭圆形织构更有利于降低密封端面的摩擦因数。随后，Qiu等[8-9]采用数值方法研究了单个球体、圆形、椭圆体、椭圆形、三角形、V 形织构对气体滑动轴承承载力、摩擦因数与轴承刚度的影响，指出椭圆体织构具有最高的承载力、最低的摩擦因数和最高的液膜刚度。Xie等[10]通过实验研究发现，相比于圆形织构和尖部逆着旋转方向的三角形织构，尖部顺着旋转方向的三角形织构更有利于降低密封端面的摩擦因数。同时，一些学者基于仿生工程也提出了非规则形状织构，分析了摩擦学特性。例如，Meng 等[11]根据硅藻壳设计了一种复合型织构，数值结果表明与简单的织构相比，复合型织构具有更大的承载力和更小的摩擦因数；李俊玲等[12]采用正交实验法确定了葫芦形织构的最优值，实验结果表明，相比于圆凹坑织构和光滑表面，葫芦形织构表面具有更低的摩擦因数；Uddin 等[13]设计了一种“星形”织构，数值结果表明，这种星形织构具有比椭圆形、人字形、三角形和圆形织构更低的摩擦因数。

近年来，一些研究者尝试对非规则织构形状进行参数化优化研究，即采用样条曲线或控制点来构造织构的几何轮廓，基于通用智能优化算法（如序列二次规划算法、遗传算法）寻优，获得了一些具有优良摩擦学性能的非规则织构形状。例如，Shen等[14]以最大承载力为目标函数，采用序列二次规划算法研究动压润滑单向和双向滑动条件下的最佳织构形状，结果表明在单向滑动下最佳形状类似V字形，双向滑动下最佳形状类似一副对称的“梯形”，在同一参数下，与圆形、椭圆形、方形、六边形与菱形相比，类似V 形织构具有较大的承载能力。随后，Shen 等[15]又对端面密封的单个织构形状进行了研究，并将V形织构与规则织构进行实验对比，得出不同面积比下最佳形状都类似V 字形；Zhang等[16-17]以摩擦因数为目标函数，采用遗传算法对处于往复运动和单向运动下的织构形状进行了研究，指出子弹形和鱼形织构适合于单向运动工况，往复运动最优织构形状类似椭圆形和纺锤形，且实验证明了在高速轻载工况下具有更低的摩擦因数；Wang等[18-19]基于多目标遗传算法对干气密封端面的表面织构形状进行了多目标优化，理论和实验结果表明：在相同的泄漏率下，相对于圆形、椭圆形、方形、三角形等规则形状而言，非对称V 字形织构具有较好的承载能力和密封性能。由此可见，通过形状优化获得的非规则V形织构比规则织构具有更优的摩擦学性能。

然而，上述尺寸优化和形状优化方法限于固定的拓扑结构，难以通过改变点线面的拓扑关系来进一步提升密封端面的摩擦学性能。据此，国内外学者引入拓扑优化方法来研究最佳织构形状以及织构深度分布规律。例如，Buscaglia 等[20]采用灵敏度分析和遗传算法研究表面织构的深度分布规律；Waseem 等[21-22]针对基于均化理论的双尺度模型，通过均匀化方法来优化织构结构，从而达到优化织构化表面宏观性能的目的；Codrignani 等[23]提出一种基于伴随方法的拓扑优化策略来研究满足质量守恒空化算法下织构深度分布规律。

水平集法作为一种拓扑优化算法，由于具备非参数描述曲线曲面、方便追踪拓扑关系的特征，广泛应用于结构拓扑优化领域[24-26]。本课题组[27]在前期研究中提出了一种基于水平集法的表面织构优化方法，以最大液膜承载力为优化目标获得了一种非规则V 形织构形状。由于前期的研究工作[27]仅研究了单个最佳织构，均布的V 形织构阵列是否有利于提升密封端面承载能力等性能有待进一步确认。据此，本文基于上述研究工作，通过多段三次贝塞尔曲线拟合上述V 形织构的轮廓边界，将其应用于机械密封端面，通过建立密封端面液膜的分析模型，研究非规则V 形表面织构几何参数及密封工况参数对密封性能的影响，并与三角形（特指等边三角形）和圆形织构密封端面进行对比，为进一步提高微织构化端面的密封性能提供支持。

1 理论模型

1.1 几何模型

图1(a)所示为织构化机械密封端面，在其静环的密封端面上采用激光技术加工出非规则V 形、三角形和圆形织构。由于织构沿密封端面周向呈现均匀分布，为方便研究，沿周向方向取一列织构作为研究对象，如图1(b)所示。图中ω为动环角速度，ri、ro分别为密封端面的内外半径，po、pi分别为密封端面外径处和内径处的压力，h0为密封间隙，hg为微织构深度。另外，周期列数为N，单列织构的径向开孔数目为Np。

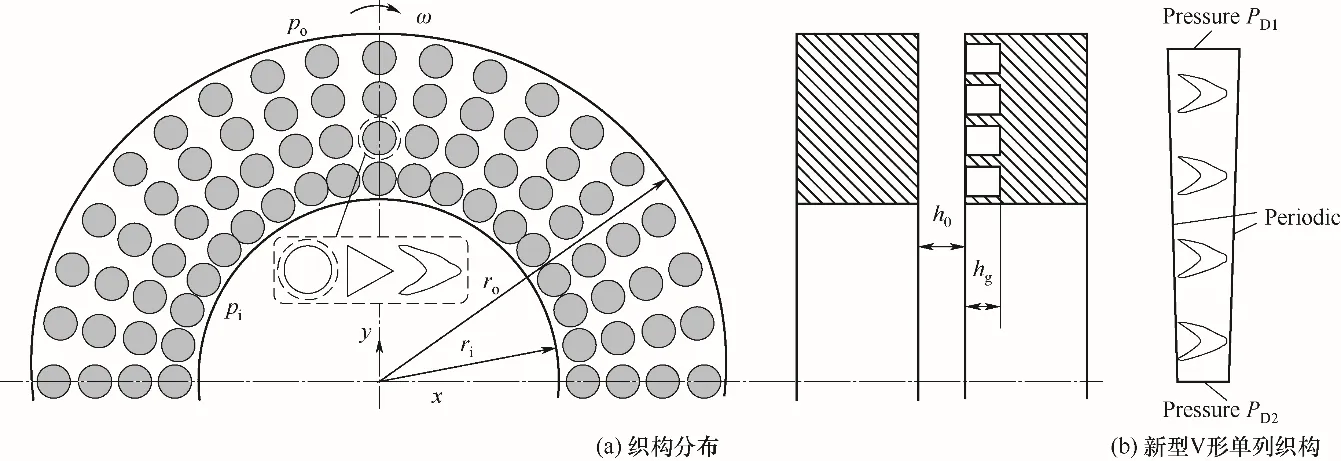
图1 表面织构化的机械密封示意图Fig.1 Schematic diagram of mechanical seal with textured surface

1.2 数学模型

假设密封端面间润滑液膜处于层流状态，充满着不可压缩牛顿流体，忽略密封端面粗糙度、表面变形、流体惯性及温升的影响，则液膜可由基于JFO(Jakobsson-Floberg-Olsson)空化算法的雷诺方程[28-29]描述，如式(1)和式(2)所示。

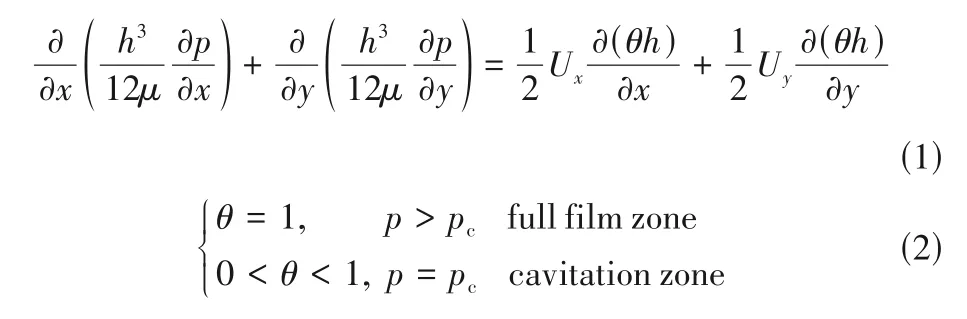
式中，h为液膜厚度；μ为液膜动力黏度；p为液膜压力；pc为密封介质的空化压力；Ux、Uy分别为动环沿x、y轴方向的滑动速度；密度比θ是液膜密度ρ与液膜液体状态下密度ρL的比值。

为了得到通用性规律，在本文中使用无量纲分析方法。对式(1)和式(2)进行无量纲化得到式(3)和式(4)。

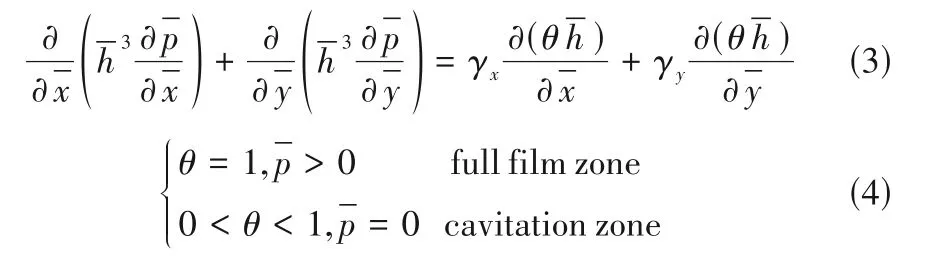
式中无量纲项定义如下。

式中，pa为大气压力；Λ为密封端面的特征数。

单列织构[图1(b)]除了周向上设置周期性压力边界条件外，还需在内外径处添加压力边界条件。内外径处的压力边界条件如式(6)所示。

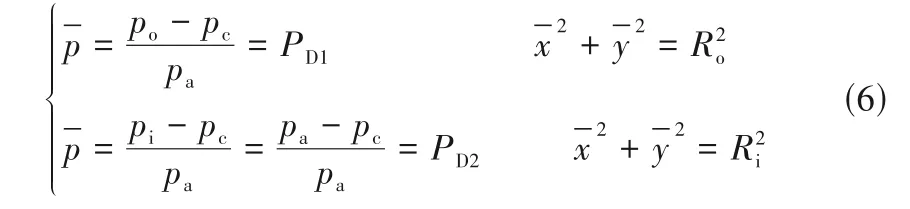
式中，PD1与PD2分别为无量纲外径与内径压力；Ri与Ro分别为无量纲内外半径。

采 用 SUPG (Streamline-Upwind∕Petrov-Galerkin) 有限元方法[28-29]求解上述无量纲方程，获得端面液膜压力分布与密度比后，密封的主要性能参数（承载力LCC、泄漏率Q、摩擦因数f和液膜刚度Kz）分别采用式（7）～式（10）求得，计算模型和方法已做了正确性验证。其中，摩擦因数f[式(9)]推导结果同文献[30]。

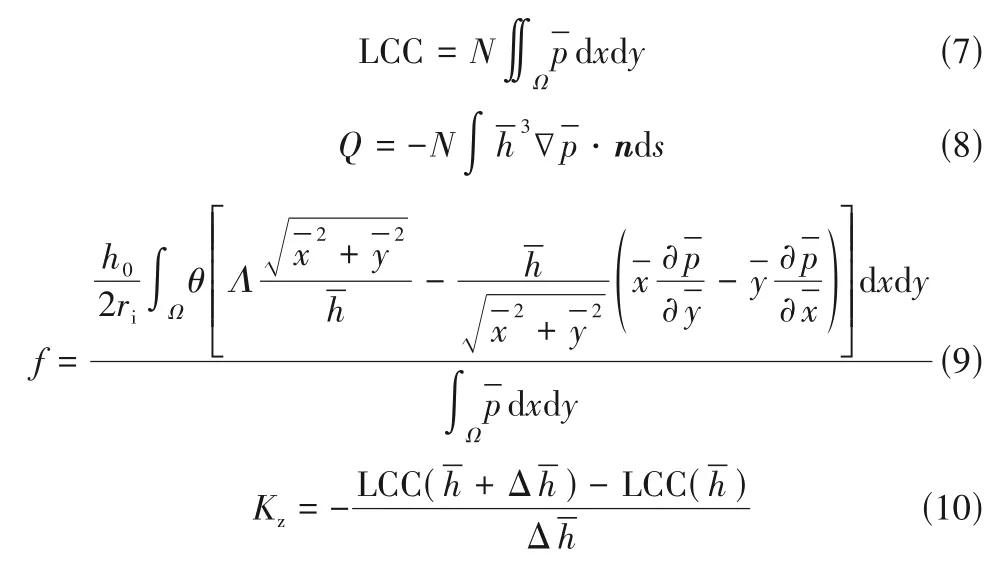
式中，Ω为一个周期单元的计算域；n为弧线上的外法线向量；s为一个周期单元的内径弧长；Δ-h为膜厚的微扰量。

2 结果与讨论

为了便于对比分析，在研究中选取以下结构参数和工况参数进行计算。

(1)结构参数

密封环端面内半径ri= 24 mm，外半径ro= 34 mm，基础膜厚h0=2.5 μm，孔深hg=5 μm，无量纲内半径Ri=1，无量纲外半径Ro=ro∕ri=1.417，织构深度比ζ=hg∕h0=2，周期列数N=120，单列织构的开孔数目Np=8，密封端面开孔的面积比AR=20%。

(2)工况参数

大气压力pa=0.1 MPa，空化压力值pc=0 MPa，密封内径处压力pi=0.1 MPa，密封外径处压力po=1 MPa，密封介质为水[动力黏度μ=1×10-3Pa·s(20℃)]，动环角速度ω=170 rad∕s，无量纲内径压力PD2=1，无量纲外径压力PD1=10，特征数Λ=942。

在下述分析参数对密封性能的影响研究中，除特别说明外，其他结构参数和工况参数均保持不变。

2.1 膜压分布

图2 所示为相同开孔数目和开孔面积比AR 下不同织构形状的液膜压力分布。由图可知，非规则V 形织构与三角形织构的无量纲压力峰值分别为11.8与11.5，位于织构的尖峰位置，而圆形织构的无量纲压力峰值为10.9，远小于V 形织构和三角形织构。这是由于在密封动环的周向剪切作用下，润滑液膜受到前两种织构两侧边界的导流作用，在织构尖部汇聚叠加而成，故无量纲压力峰值相对较大，尤其是非规则的V 形织构，其两侧的楔形几何构型的导流作用更强，因此其动压效应在三种织构中也是最强的。由液膜最低压力可见，圆形织构具有最低的液膜压力，非规则V形织构次之，而三角形织构最大。

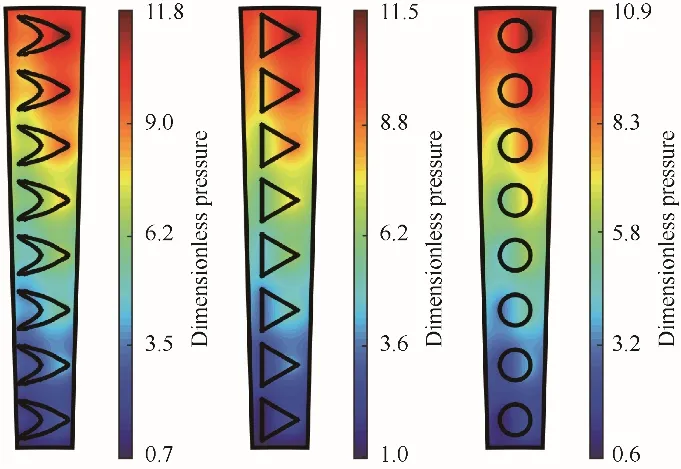
图2 不同织构形状的密封端面液膜压力分布Fig.2 Pressure distribution of seal face with different texture shapes

2.2 几何参数对密封性能的影响

2.2.1 开孔面积比的影响 开孔面积比AR 是微织构面积与一个周期单元面积的比值。图3所示为在不同织构形状下开孔面积比AR 对机械密封性能的影响，其中开孔面积比AR 的变化通过保持开孔数目不变，改变单个织构面积获得。值得注意的是，V形织构通过多段三次贝塞尔曲线拟合获得，其特征尺寸为贝塞尔曲线的控制点，通过控制点的坐标变换来实现V形织构面积的改变。

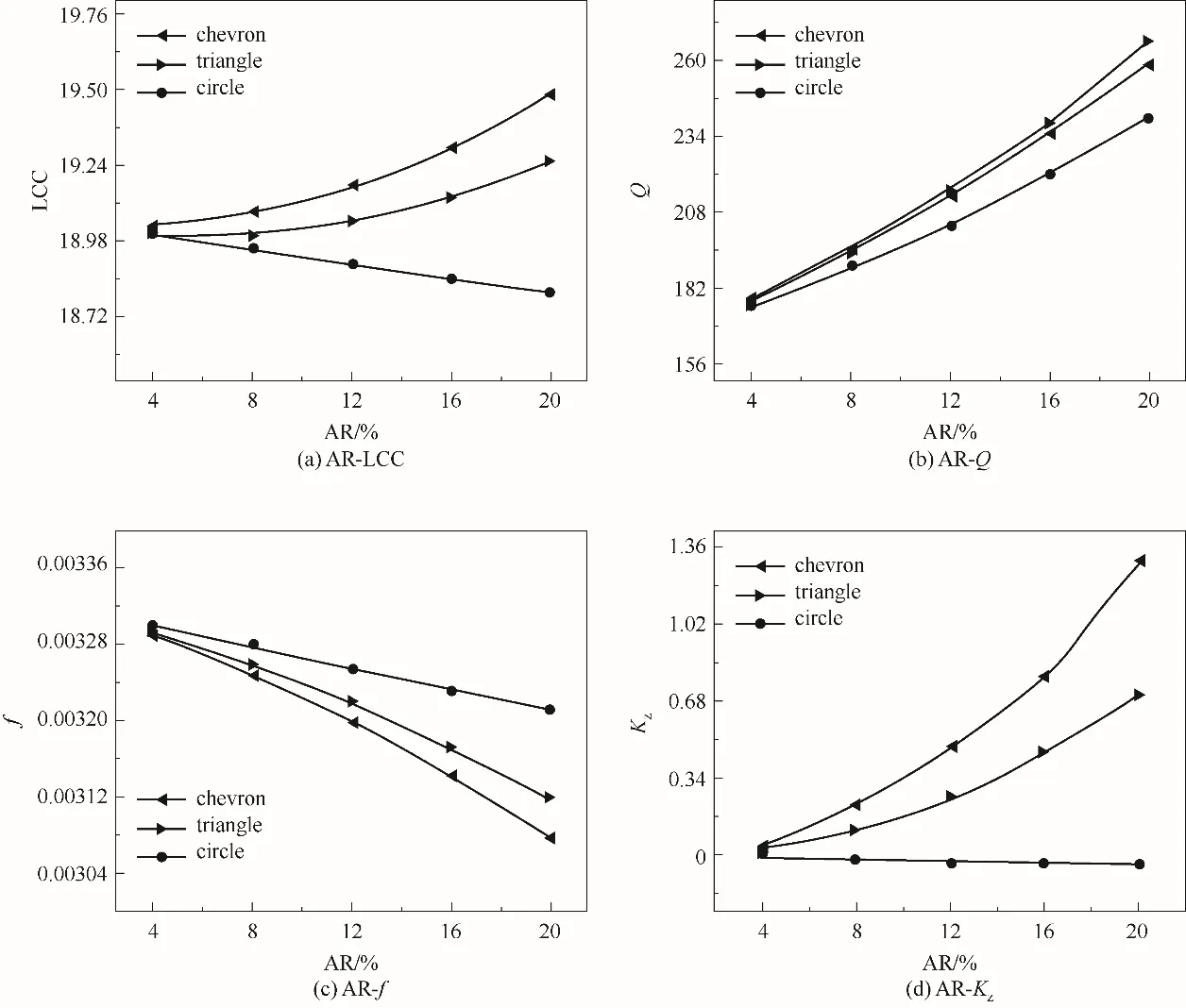
图3 开孔面积比对机械密封性能的影响Fig.3 Effect of area ratio on mechanical seal performance

由图3(a)可知，随着AR 的增大，V 形与三角形织构的承载力逐渐增大，而圆形织构的承载力呈缓慢下降的趋势，且下降幅度较小。同时，在同一AR下V形织构的承载力最大，三角形织构次之，圆形织构最小，这是因为V 形和三角形织构的尖部能汇聚流体，从而增强动压效应。当AR 大于10%时，承载力增大趋势较为显著。从图3(b)可得，三种织构的泄漏率均随着AR 的增大而增大，且在同一AR 下，泄漏率由大到小依次为三角形织构、V 形织构与圆形织构。当AR 小于10%时，V 形织构和三角形织构的泄漏率结果相差较小。由图3(c)可知，随着AR的增大，三种织构的摩擦因数均呈现下降的趋势，与泄漏率变化规律相反，这是因为承载力起主导作用，承载力越大，摩擦因数越小，且在同一AR 下圆形织构的摩擦因数最大，V形织构最小。比较而言，当AR 大于10%时，V 形织构的优势更为明显。由图3(d)可知，随着AR 的增大，V 形织构与三角形织构的液膜刚度均呈现上升的趋势，而圆形织构的液膜刚度基本保持不变，且在同一AR 下V 形织构的液膜刚度最大，圆形织构最小。这是因为液膜刚度反映了膜厚的微扰动对流体动压承载力的改变能力，受流体动压效应的影响，因而液膜刚度变化规律与承载力一致。综上所述，开孔面积比AR 的变化对V 形与三角形织构的密封性能影响较大，而对圆形织构的密封性能影响不大。当AR 一定时，三种织构中V 形织构的承载力、摩擦因数与液膜刚度均最优，且泄漏率略小于三角形织构，当AR 大于10%时这种效果更为明显。当AR 小于10%时，密封性能参数相差相对较小。

2.2.2 织构深度比的影响 图4为在不同织构形状下深度比ζ对机械密封性能的影响规律。

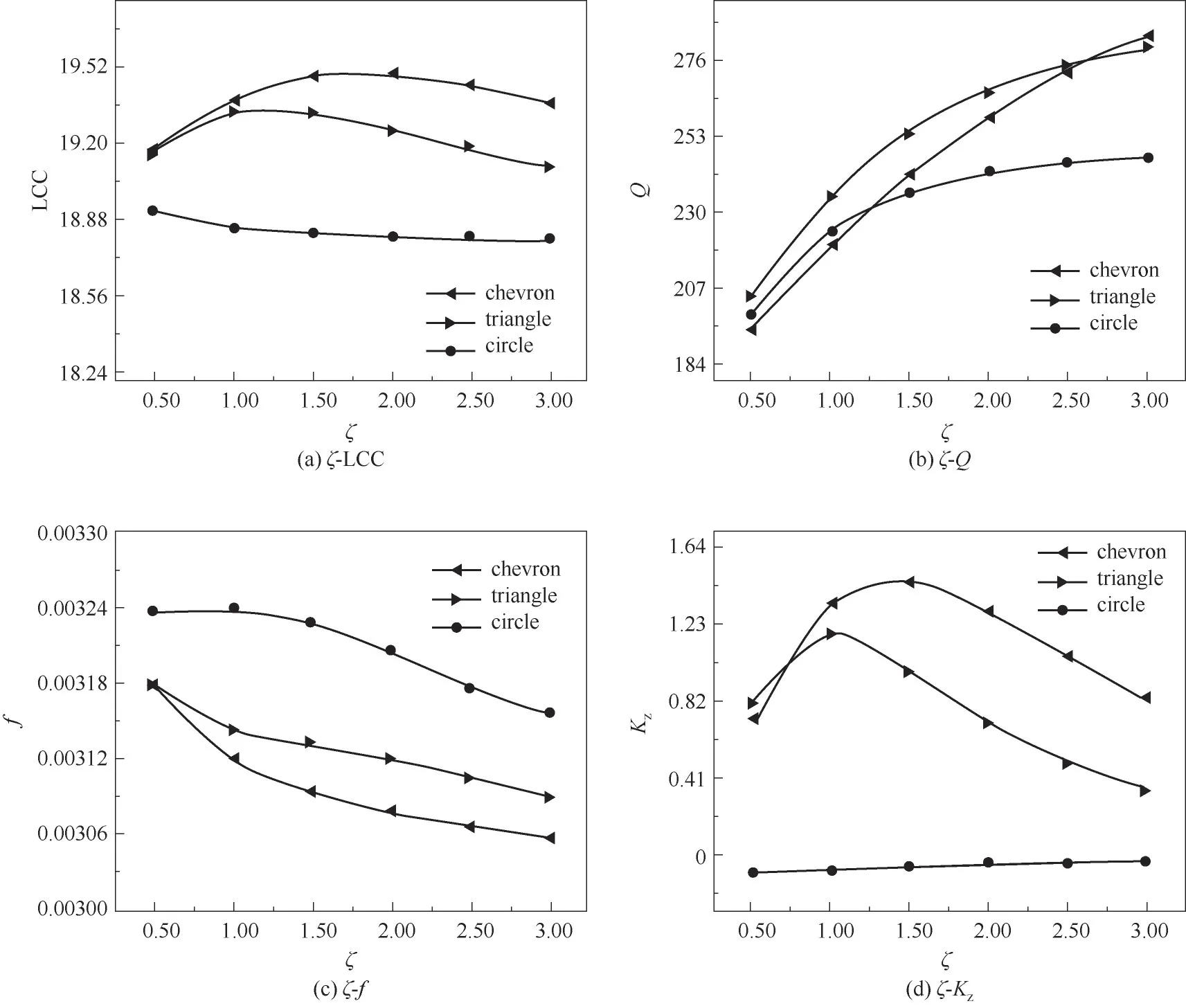
图4 深度比对机械密封性能的影响Fig.4 Effect of depth ratio on mechanical seal performance

由图4(a)可见，随着织构深度比ζ的增加，非规则V形与三角形织构的承载力均呈现先增大后减小的变化规律，且V形织构的承载力大于三角形织构，当ζ大于1.00 时，这种效果更为明显，在ζ约为1.77时，V形织构的承载力得到最大值，而圆形织构的承载力基本不变，这是因为在液膜未发生空化的条件下，具有对称性的织构不具有良好的动压效应，与流体动压效应强弱程度有关。由图4(b)可见，随着ζ的增大，三种织构的泄漏率均呈现增大的趋势，且V形织构的泄漏率增大程度远大于其他两种织构，圆形织构的增大程度最小。由图4(c)可见，随着ζ的增加，三种织构的摩擦因数均呈现缓慢减小的趋势，且在同一ζ下V 形织构的摩擦因数最小，而圆形织构的最大。由图4(d)可见，液膜刚度的变化规律与承载力变化规律类似，随着ζ的增加，V 形与三角形织构的液膜刚度均呈现先增大后减小的趋势，且V形织构的液膜刚度逐渐大于三角形织构，当ζ=1.50时，液膜刚度达到最大值，而圆形织构的液膜刚度随ζ的增加变化不大，在同一ζ下圆形织构的液膜刚度最小。综上可知，织构深度比的变化对V 形与三角形织构的密封性能影响较大，而对圆形织构影响不大，在同一深度比下，V 形织构的承载力、摩擦因数与液膜刚度均相对最优，且在ζ大于1.00 时，这种效果更为显著，但同时泄漏率亦呈现逐渐增大的趋势。

2.3 工况参数对密封性能的影响

2.3.1 特征数的影响 图5所示为不同织构形状下不同特征数Λ对机械密封性能的影响规律。特征数Λ是与密封转速正相关的无量纲数，转速越大，特征数越大。

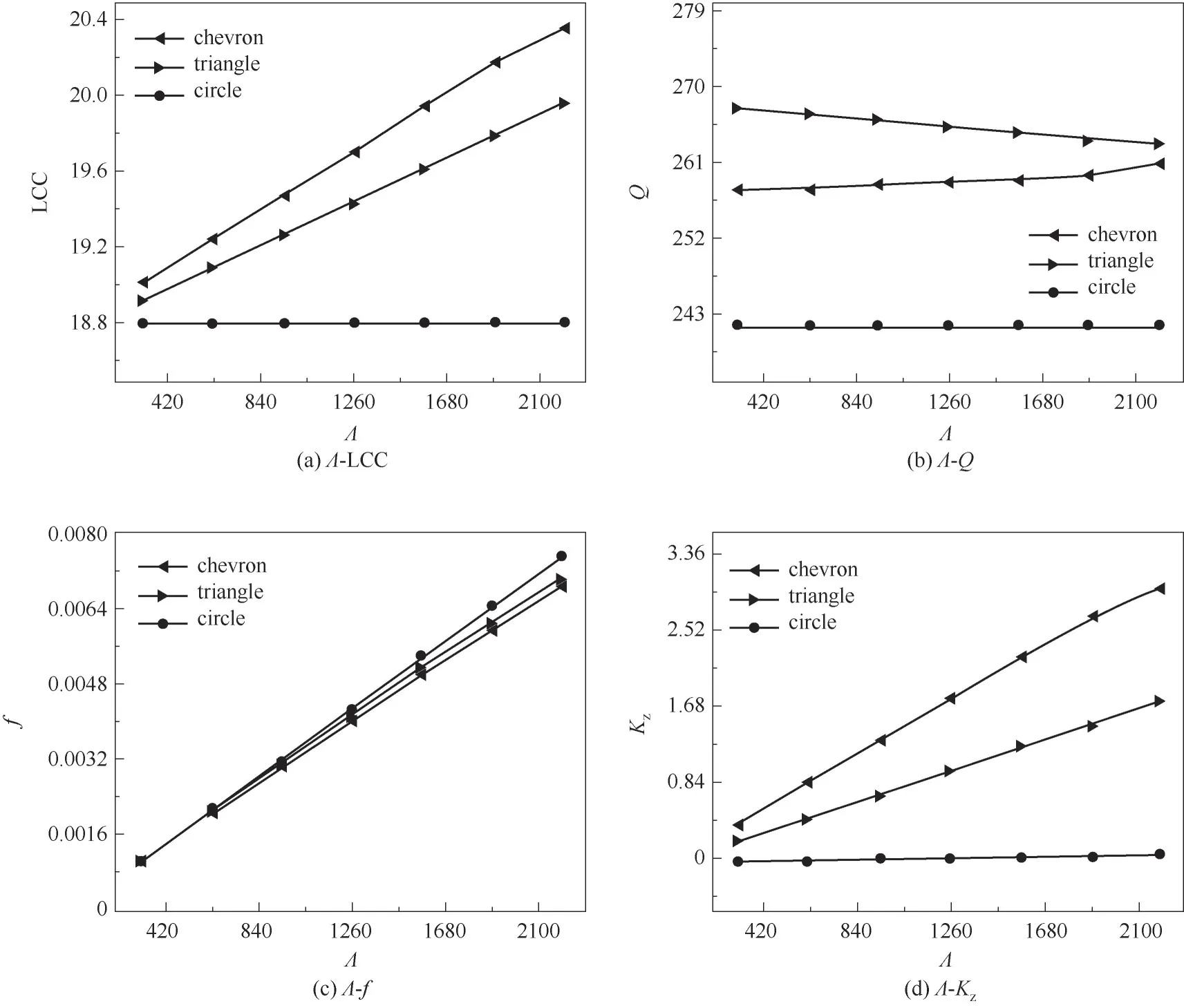
图5 特征数对机械密封性能的影响Fig.5 Effect of characteristic number on mechanical seal performance

由图5(a)可见，由于流体动压效应随着Λ的增大而持续增强，因此随着Λ的增大，V 形织构和三角形织构的承载力均呈现线性增大的变化规律，而圆形织构的承载力基本不变，且在同一Λ下V 形织构的承载力最大，圆形织构最小。由图5(b)可见，随着Λ的增大，三种织构的泄漏率变化趋势不同：V 形织构上升趋势非常缓慢，基本没有太大的变化，三角形织构呈现缓慢下降的趋势，而圆形织构基本保持不变。在同一Λ下，三角形织构的泄漏率最大，而圆形织构的泄漏率最小。由图5(c)可见，三种织构的摩擦因数随着Λ的增大而增大，且三种织构摩擦因数的变化曲线几乎一致。特征数Λ随着密封环角速度的改变而改变，由于转速增加，Λ增加，液膜的黏性剪切作用增强，故摩擦因数增大。同时，在同一Λ下，圆形织构的摩擦因数增长速度最大，V形织构最小，且随着Λ的增大，这种效果越显著。当Λ小于1260 时，三种织构的摩擦因数差别不大。由图5(d)可见，液膜刚度的变化规律与承载力的变化规律类似，随着Λ的增大，V 形与三角形织构的流体动压效应持续增强，其液膜刚度呈现线性增大的趋势，而圆形织构的液膜刚度基本保持不变，且在同一Λ下V 形织构的液膜刚度最大，圆形织构最小。综上可知，在相同的特征数Λ下，V 形织构的承载力、摩擦因数与液膜刚度最优，泄漏率虽呈现出缓慢增大的趋势，但增大趋势较小。

2.3.2 密封介质压力的影响 图6所示为不同织构形状下不同密封介质压力PD1对机械密封性能的影响。由图6(a)可见，随着PD1的增大，液膜流体的静压效应得到持续增强，三种织构的承载力呈现出线性增大的变化规律，且三种织构的变化曲线几乎一致。由图6(b)可见，随着PD1的增大，三种织构的泄漏率均持续线性增大。这是由于密封介质压力的增大使得密封端面内外半径的静压差增大，致使沿泄漏方向的压力梯度变大，从而导致泄漏率的增加。由图6(c)可见，随着PD1的增大，三种织构的摩擦因数均呈现出逐渐下降的趋势，这是因为承载力起主导作用，承载力越大，摩擦因数越小。由图6(d)可见，由于密封介质压力的变化增强了液膜的静压效应，因此随着PD1的增大，液膜刚度随密封介质压力的变化不大，三种织构的液膜刚度基本保持不变，但在同一PD1下，V 形织构的液膜刚度最大，约是三角形织构的2 倍，而圆形织构最小，基本保持在0 附近。综上可知，密封介质压力的变化对三种织构的机械密封性能影响较大，且在相同的介质压力条件下，三种织构的承载力、泄漏率和摩擦因数结果相差不大，但V 形织构的液膜刚度最优，约是三角形织构的2 倍，而圆形织构的液膜刚度最小。

图6 密封介质压力对机械密封性能的影响Fig.6 Effect of seal medium pressure on mechanical seal performance

3 结 论

本文采用有限元数值模拟方法研究了新型非规则V 形表面织构对机械密封性能的影响，探讨了不同几何参数和工况参数下承载力、泄漏率、摩擦因数和液膜刚度等密封性能参数的变化规律，并与三角形和圆形表面织构进行了对比优选分析，具体结论如下。

（1）相比于圆孔织构和三角形织构，新型非规则V形织构上下两侧的楔形结构具有明显的收集和汇聚液膜的作用，使其具有更强的动压效应和液膜承载力，开孔面积比、深度比、密封特征数和密封介质压力对V形织构与三角形表面织构的密封性能具有较大影响，而对圆形织构的密封性能影响不大。

（2）在研究几何和工况参数范围内，新型V形表面织构的机械密封性能相对较优，其承载力、摩擦因数与液膜刚度均略优于三角形织构，远优于圆形织构；对于泄漏率，虽然V形织构泄漏率略低于三角形织构，但呈现增长的趋势。

（3）当织构开孔面积比AR 大于10%、深度比ζ大于1.00 时，V 形织构具有比三角形织构和圆形织构更明显的优势，且在ζ约为1.77 和1.50 时，V 形织构的承载力和液膜刚度分别达到最大值；在不同密封压力下，V 形织构的液膜刚度可达三角形织构的2倍。