肋片和多孔介质强化梯级相变储热系统性能的对比研究
2022-11-13沈永亮张朋威刘淑丽
沈永亮,张朋威,刘淑丽
(北京理工大学机械与车辆学院,北京 100081)
引 言
相变材料(PCM)由于较高的潜热蓄热能力、恒定的固液相变温度和低成本等优点[1-2],已经被广泛应用于可再生能源或废热储热系统[3-5]。但PCM 通常具有较低的热导率,这强烈限制了其实际应用[6-8]。Farid 等[9]首次提出了梯级相变储能的概念,以增加传热流体(HTF)和PCM 之间的温差。在加热过程中,入口HTF 温度高于所有PCM 的相变温度,并且这些相变温度沿着HTF 流动方向逐渐降低。在放热过程中,HTF 的流动方向与加热过程相反[10-11]。基于这一传热原理,与单个PCM 储热系统相比,梯级相变储能系统在热性能方面的优势[12-14]包括:(1)均匀化传热温差来提高系统的传热速率;(2)降低HTF 出口与环境的温差,减少热量和损失;(3)实现不同温度范围内热量的梯级利用。为了获得更好的热性能,对梯级相变储能系统的性能进行了广泛的研究。大量研究表明,梯级相变储热技术在能源效率、效率和热效率方面具有优势[15]。此外,梯级PCM 系统的优势不仅在于热速率输出的增加,而且还具有减少PCM 质量、设备体积和经济投资的潜力[16]。
杨 兆 晟 等[17-18]设 计 了 以 EG-MgSO4·7H2O·KAl(SO4)2·12H2O 复合相变材料、硬脂酸、60 号石蜡作为三级的梯级相变储热器,相比于单级相变储热器的储热量、蓄放热时间、储热效率以及热回收效率均有较大提高。Mahdi 等[19]研究了使用梯级PCMs、具有纳米颗粒的梯级PCMs 和具有金属泡沫的梯级PCMs 的不同排列对相变凝固演化的影响。结果表明:与单PCM 应用相比,双PCMs 和三PCMs应用的固化过程分别加快了5.2% 和8.7%;平均温度随着多相PCMs 数量的增加而降低;引入纳米颗粒和金属泡沫显著增强了传热过程,节省了凝固时间。Mahdi 等[20]在三级相变储能中采用新型肋片实现了更高的PCM 熔化速率。
在目前的研究中,组合强化传热后的梯级相变储能系统研究仍然缺乏。此外,二维相变换热数值模拟研究较多,三维尺度梯级相变储能系统层面的数值模拟研究工作缺乏,无法真实反映翅片等技术对系统的强化作用。本文通过对梯级相变储能系统的放热过程进行三维数值模拟仿真研究,建立无肋片和多孔介质、无肋片有多孔介质、有肋片无多孔介质、有肋片和多孔介质四种三维数值模型,分析比较不同方法对放热过程的强化作用。对三种相变材料孔隙率进行梯级布置,研究比较正梯度、无梯度和负梯度三种情况下梯级相变储能系统的放热性能。
1 数值模型建立与实验验证
1.1 材料
本文研究中月桂酸、石蜡和硬脂酸被选作梯级相变储能系统的PCM,差示扫描量热仪(DSC)测试结果如图1 所示。月桂酸的相变温度约为44 ℃,相变焓值为187740 J∕kg;石蜡的相变温度约为58 ℃,相变焓值为182240 J∕kg;硬脂酸的相变温度约为68 ℃,相变焓值为227160 J∕kg。此外,本文还考虑了多孔复合相变材料对系统性能的影响,多孔介质和三种PCM的具体参数如表1所示。
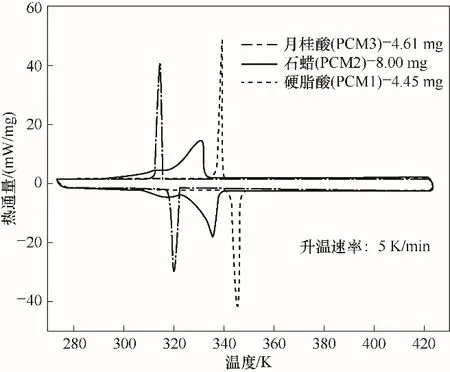
图1 相变材料的DSC曲线Fig.1 DSC curves of phase change materials
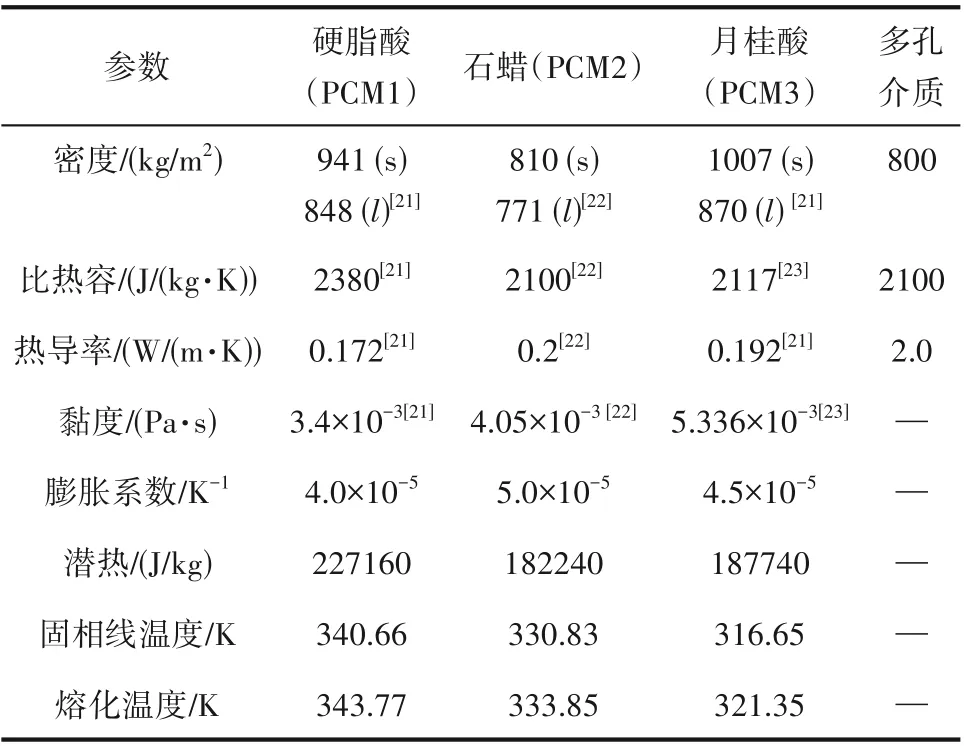
表1 相变材料与多孔介质的物性参数Table 1 Physical parameters of PCMs and porous media
1.2 物理模型
设计了一种梯级相变储能系统,由三级串联的肋片增强型三管壳式储热器构成。储热器的结构如图2 所示,内管和外管为传热流体(HTF),中管为PCM 腔体,矩形肋片与内外管道均匀连接。为了使得传热流体与PCM 换热时达到稳定流动状态,在储热器的两端设置了密封盖,几何参数如表2所示。
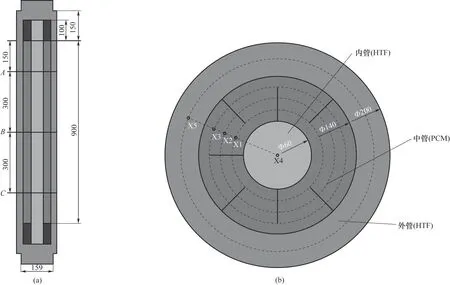
图2 相变储热器结构示意图(单位:mm)Fig.2 Schematic diagram of the latent heat storage unit
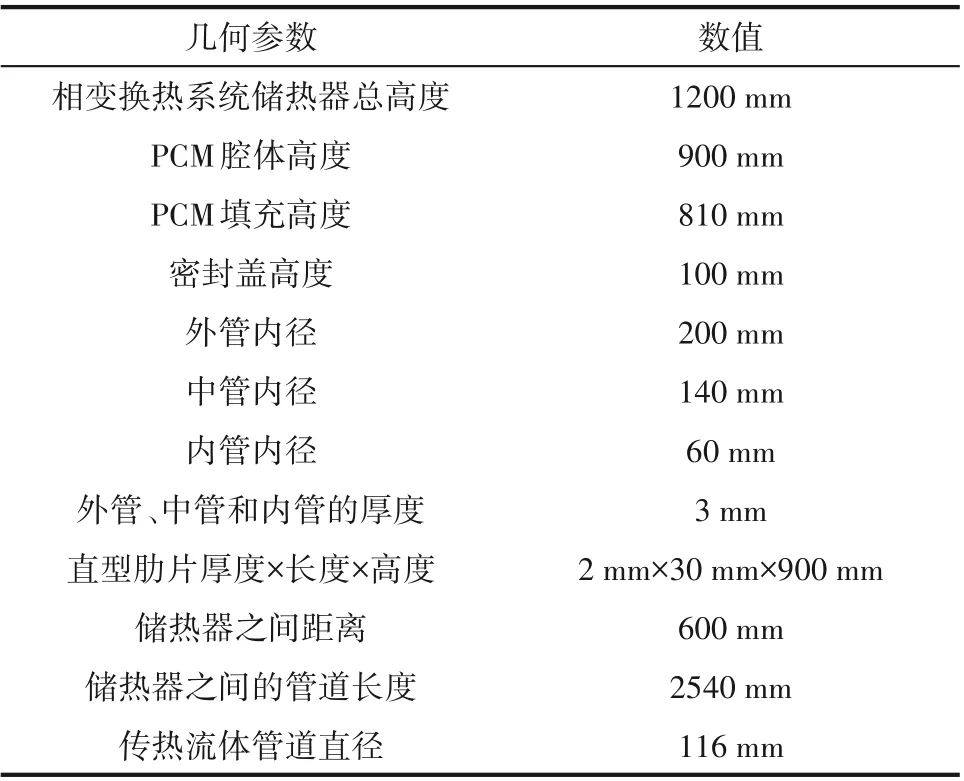
表2 相变储热器物理模型的具体几何尺寸参数Table 2 The specific geometric parameters of the physical model of the latent heat storage unit
建立了三维仿真物理模型,考虑到物理模型结构较为复杂且存在多域计算,采用非结构化混合型网格(图3),内外直肋片和相变区域做加密处理保证计算结果更加准确,对各类边界和几何体进行命名,边界层设置为5 层平滑过渡,网格增长率为1.2,过渡比为0.2。此外,相同区域的接触面进行组合处理,便于后期FLUENT 求解器中边界条件的耦合设置。
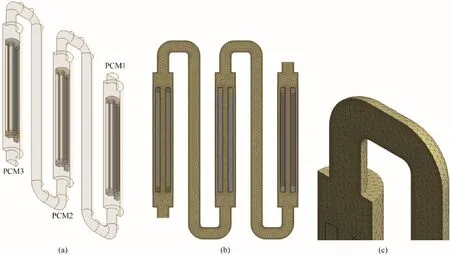
图3 梯级相变储热系统物理模型和网格结构Fig.3 Physical model and mesh grids of cascaded latent heat storage system
1.3 数学模型
对三维传热模型做出了以下假设[24-26]:
①各级相变材料相变温度稳定,多次工作循环后热物性参数不发生改变;
②液态相变材料为牛顿型不可压缩流体;
③多孔介质被认为是均匀的和各向同性的;
④忽略相变过程中的体积变化,密度采用Boussinesq假设,考虑浮升力作用;
⑤认为相变材料相变状态始终处于局部热平衡状态,忽略黏性耗散;
⑥储热器外壁面绝热,忽略储热器对外部环境散热产生的热损失。
求解区域可以分为传热流体区域和相变材料区域,两个控制区域内的流动传热受质量守恒、动量守恒以及能量守恒三大定律共同作用。方程的具体形式如下所示。

式中,V为速度矢量,m∕s;μf为热流体动力黏度,Pa·s;λf为传热流体热导率,W∕(m·K);CPf为热流体比定压热容,J∕(kg·K);ρf为热流体密度,kg∕m3;T为储热器内热流体温度,K。
(2)相变材料区域

式中,ε为随机小数(小于0.0001,防止出现分母为0 的情况);Amush为糊状区常数(理想值介于10-5和10-6,此处取10-5);μ为相变材料的动力黏度,Pa·s;Ci为惯性常数;K为渗透率;β为PCM的液相率。
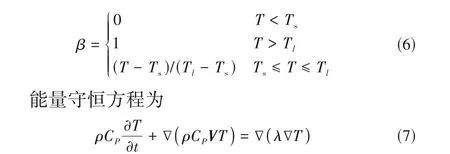
式中,λ是PCM 的热导率,W∕(m·K);对于多孔复合相变材料,多孔介质影响的有效热导率与孔隙率ϕ有关,按照式(8)计算得到[28-30];CP为相变材料的等效热容,可以通过式(10)得到[28]。

式中,λfin为金属肋片的热导率,W∕(m·K);ρfin为金属肋片的密度,kg ∕m3;CP,fin为金属肋片的比热容,J ∕(kg·K);TPCM为相变材料的温度,K;Tfin为金属肋片的温度,K。
1.4 边界条件设置
根据梯级相变实验系统的运行情况,三维数值模型的进口边界条件为恒定进口温度和流速,为

1.5 放热特性
PCMs的放热量表示为
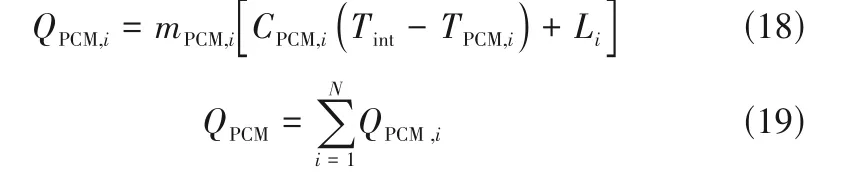
式中,i表示第i级PCM;mPCM为相变材料质量,kg;CPCM,i为相变材料的比热容,J∕(kg·K);L为相变材料的潜热,J∕kg;下角标int表示初始状态。
因此,PCMs 的放热速率可以写成式(20)和式(21)。

因此,PCM 放热过程中的能量效率可以定义为PCM 释放的能量与HTF 吸收的能量之比,如式(24)和式(25)所示。

2 数值计算方法和模型验证
2.1 数值计算方法
根据传热流体的流速和管径确定传热流体处于湍流状态,因此计算模型中传热流体使用k-ε湍流模型,Solidification∕Melting 模型用于处理PCM 的相变过程。求解方法采用压力和速度耦合方式选择Coupled 算法,压力修正方程采用PRESTO 方案,其他各项方程离散方式均使用二阶迎风格式。压力、密度、速度、液相分数、能量亚松弛因子分别设为0.3、0.5、0.7、0.8和0.9。
2.2 无关性验证和模型验证
在本次模拟中,根据网格数2倍递增原则,保证计算精度的同时划分了四组网格,网格数分别为428198、922625、2143483、3149660 个。在相同的求解器参数设置前提下,分别对以上四种网格数的数值模型进行计算,采用相变区域体积加权平均方法来表示相变区域的相变情况,得到了不同网格数下PCM1 的液相率随温度的变化情况。为了确定数值模拟的时间步长,选择了三种时间步长进行验证,分别为0.1、0.5 和1.0 s,比较了三种时间步长PCM的液相率变化情况。为了验证数值模型的准确性,搭建了与物理模型完全一致的实验系统(图4),在进口温度为373.15 K,进口流速为4.8 m∕s 条件下对数值模型的加热和放热过程进行验证。

图4 梯级相变储热实验系统的示意图和实物图Fig.4 Schematic and physical diagram of the experimental cascaded latent heat storage system
如图5(a) 所示,由网格数922625 个向2143483个过渡时,液相率达到1时的时间变化明显,而网格数继续增长到3149660 个后时间则几乎没有变化,认为此时已经达到了网格无关要求,最终确定最优网格数为2143483 个。时间步长无关性验证如图5(b)所示,时间步长分别为0.1、0.5 和1.0 s 时,PCM 的液相率变化几乎相同,为了节约计算时间成本,选择1.0 s 作为数值模拟的时间步长。实验数据与模拟数据的温度变化趋势如图5(c)所示。可以看出,两组数据能够较好地吻合,证明数值模型以及求解方法的正确性。实验数据平均温度(337.35 K)与模拟数据平均温度(339.77 K)的偏差约为2.4 K,在允许误差范围内。
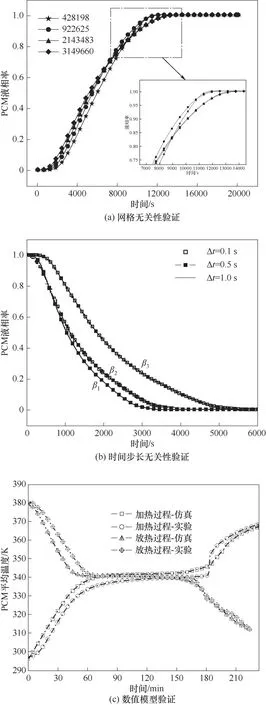
图5 网格无关性验证和数值模型验证Fig.5 Mesh independence and numerical model verification
3 数值仿真结果与讨论
3.1 肋片和多孔介质对放热过程的影响
对添加肋片和多孔介质的梯级相变储能系统放热过程进行数值模拟,分别进行四种情况下的模拟仿真:(1)无肋片无多孔介质组;(2)有肋片无多孔介质组;(3)无肋片有多孔介质组;(4)有肋片有多孔介质组。传热流体设置为水,进口流速为0.4 m∕s,进口温度为300.00 K,储热器内PCMs的初始温度均为373.00 K,PCMs的孔隙率均为0.9。
图6为相变放热过程中四种添加肋片和多孔介质情况下PCMs 的平均温度和液相率变化规律。从图6(a)~(c) 中可以看出肋片和多孔介质对PCMs 的凝固过程影响较大,无肋片无多孔介质情况下整体的放热速率较慢,此时PCMs 只能通过套管壁面与热流体进行换热。分别添加肋片和多孔介质后放热性能显著提高,放热时间明显缩短,说明添加肋片和多孔介质都能有效提高系统整体的换热速率,同时添加肋片和多孔介质,系统放热时间进一步缩短,此种情况下梯级相变系统具有最优的放热性能。
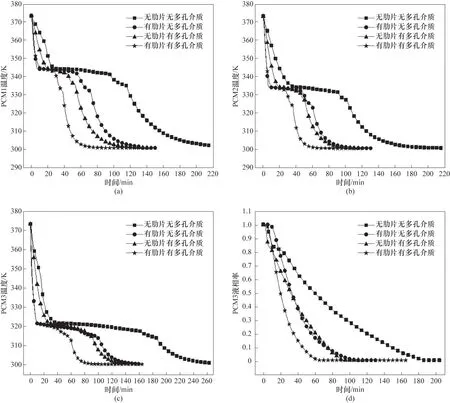
图6 肋片和多孔介质对PCMs放热过程的影响Fig.6 Effects of fins and porous media on the discharging process of PCMs
肋片对整体强化传热增强作用贯穿三个阶段,三个阶段放热时间均有缩短,在液态显热放热阶段,有肋片的两种情况表现出一致的降温速率,且比添加多孔介质的下降速率大,在固态显热放热阶段也表现出近似相同的降温速率,说明肋片的增强传热作用虽然会贯穿整个放热过程,但在显热放热段强化传热作用更具优势。而添加多孔介质的增强传热作用也会体现在整个放热过程中,三个阶段放热时间均有缩短,但在显热放热段强化传热作用略差于添加肋片结构,在潜热放热段具有更强的强化传热能力,整个放热过程只加入多孔介质比只加入肋片情况整体上表现出更好的放热性能。除此之外,添加肋片和多孔介质对PCM3 的强化换热作用要比PCM2 和PCM1 强烈,由于PCM3 本身就具有较长的放热时间,因此同时添加肋片和多孔介质能缩短系统整体放热时间,提高系统的放热效率。
四种情况下PCM3 的放热时间最长,因此可用PCM3 放热时间来代表整个梯级系统的放热时长,图6(d)为四种情况下PCM3的液相率变化规律,从图中可以看到液相率下降早期,无肋片的两组液相率表现出较快的下降速率,因为肋片的加入在一定程度上会减弱内部固液材料的对流换热作用。随着放热过程的进行,同时添加肋片和多孔介质的PCM3 在60 min 时率先完成凝固过程,单独添加肋片和多孔介质完全凝固所需时间近似相同,约为100 min,而无肋片无多孔介质时PCM3 完全凝固时间明显增长,在190 min 时液相率才降至0。同时添加肋片和多孔介质的情况下,PCM 完全凝固时间缩短了40%。
通过四种添加肋片和多孔介质情况的放热模拟数据可以看出,肋片和多孔介质的强化传热作用在整个放热过程均有体现,但在显热放热阶段肋片的增强作用更强,在潜热放热阶段多孔介质的增强作用更显著,对于整个放热过程,肋片和多孔介质增强作用在PCM2 和PCM3 中差别较小,在PCM1 中差异明显,原因是PCM1 的凝固温度较高,温差较大,能够充分体现其差异性。此外同时添加肋片和多孔介质时,系统的放热时间得到了较大的缩短,在整体放热量差别不大的情况下,能反映出该情况具有较高的换热速率和换热效率,此时梯级相变系统具有较好的放热性能。
3.2 材料孔隙率梯度对放热过程的影响
通过3.1 节的数值研究发现添加肋片和多孔介质可以有效缩短梯级相变放热过程所耗时间,显著提高换热速率,但是各级储热器的放热时间也相差很大,PCM3 严重滞后了系统的相变放热时间。通过改变各级PCMs 的孔隙率进行放热过程数值模拟研究,共设置了三种孔隙率梯度,包括正孔隙率梯度、均匀孔隙率梯度和负孔隙率梯度,具体参数见表3。
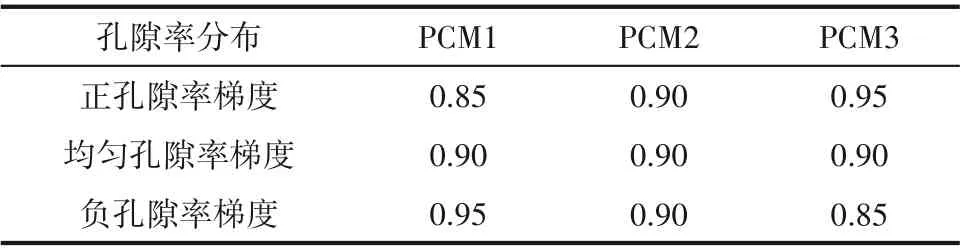
表3 三种孔隙率梯度分布情况Table 3 Three cases of gradient porosity of PCMs
三种梯度情况下PCM2 的孔隙率均为0.90,且数值仿真结果表明PCM2的变化极小,均在58.5 min左右结束放热,故选用PCM1和PCM3进行分析。图7 为三种孔隙率梯度对PCM1 和PCM3 放热过程平均温度的影响。从图7(a)中可以看出孔隙率梯度对PCM1的放热影响很明显,正梯度情况下PCM1孔隙率较小,多孔介质占比更多能充分扩大储热器内部固液材料的换热面积,增强内部的换热速率,表现为正梯度比均匀梯度具有更优良的放热性能。而负梯度情况则是相反,PCM1 材料增多,多孔介质减少,内部换热受到限制表现出比均匀梯度慢的换热速率,所以也较晚完成放热过程。图7(b) 为PCM3的温度变化规律,与PCM1 相反,负梯度时PCM3 内多孔介质占比更高,内部换热速率也提升明显,比均匀梯度更快完成放热阶段,而正梯度则会增多PCM3 而减少多孔介质,比均匀梯度更晚完成放热过程。总体上可以看出正梯度情况下PCM3 放热最慢,系统放热时间为115.0 min;均匀梯度情况下PCM3 放热最慢,系统放热时间为90.5 min;负梯度情况下PCM1放热最慢,系统放热时间为94.0 min。
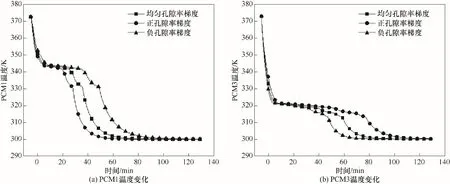
图7 孔隙率梯度对PCM1和PCM3放热温度的影响Fig.7 Effect of gradient porosity on temperature of PCM1 and PCM3
图8(a) 为PCM1 的液相率变化规律,能够较好反映相变潜热阶段的放热情况,可以看到孔隙率梯度的影响会贯穿整个潜热放热过程,从液相率下降初期就有了区别,且随着过程推进差异更加明显,可以看出正梯度更利于PCM1 完成相变潜热过程固液相的转变,该规律与温度变化规律一致。图8(b)为PCM3 的液相率变化规律,可以看出负梯度具有更高的液相率下降速率,能够较快完成液态PCM3的凝固。整体来说,无论是PCM1 还是PCM3,负梯度与均匀梯度的差异比正梯度与均匀梯度的差异小。此外,由于PCM3 放热时间更长,适当缩短PCM3的放热时间,提高PCM1的放热时间能更好实现各级储热器的均匀放热,有利于提高梯级系统放热过程的热性能。
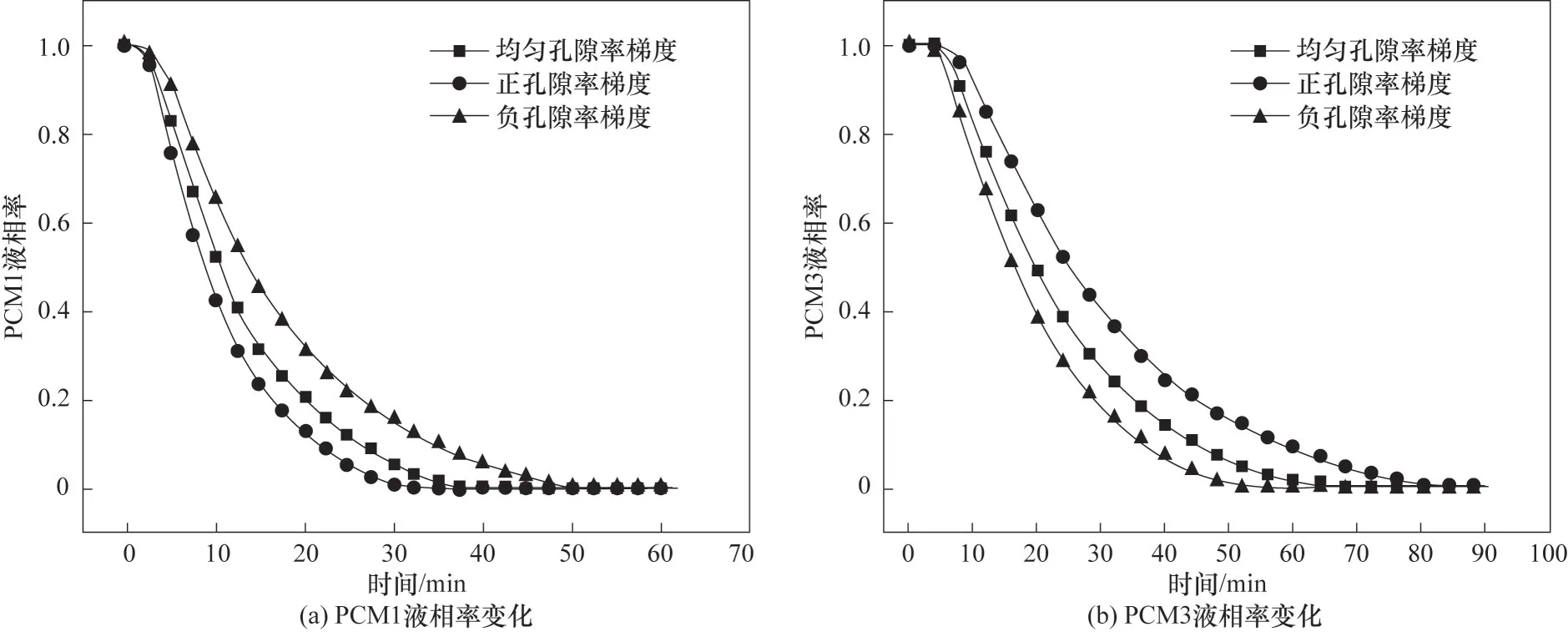
图8 孔隙率梯度对PCM1和PCM3液相率的影响Fig.8 Effect of gradient porosity on liquid fraction of PCM1 and PCM3
图9为三种孔隙率梯度情况下各储热器及梯级系统的放热速率与效率的对比,从图9(a)中可以看出正梯度情况下PCM1 的放热速率最大,为447.3 W,其次是PCM2,PCM3 放热速率最低;均匀梯度和负梯度情况下PCM2 的放热速率最大,为394.8 W,其次是PCM1,PCM3 放热速率最低。此外,随着孔隙率的降低,PCM1 的放热速率逐渐减小,而PCM3的放热速率逐渐增大,各级储热器的放热速率趋向于更加均匀。均匀梯度和负梯度情况下,梯级系统的放热速率接近,在负梯度情况下最大,为824.3 W,在正梯度情况下最低,仅为670.3 W。从图9(b)中看出正梯度情况下沿流体流动方向,PCM 放热效率逐渐增大,在第一级储热器最大,为78.3%;均匀梯度情况下流体吸热效率先增大后减小,在第二级储热器最大,为77.4%;负梯度情况下PCM放热效率逐渐减小,在第三级储热器最大,为78.3%。在三种孔隙率梯度情况下,系统的放热效率整体差异不大,均在75.0%左右。根据仿真数据结果可以看出,负梯度情况可以缩短系统放热时间,使各级储热器的放热速率更加均匀,提高系统整体的放热速率,梯级系统具有更好的放热性能。
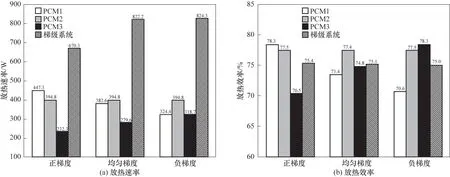
图9 孔隙率梯度对放热速率与效率的影响Fig.9 Effect of gradient porosity on discharging rate and efficiency
4 结 论
建立了梯级相变储能系统的三维数值仿真模型,并利用实验数据对模型进行了验证。利用数值方法研究对比了肋片和多孔介质对梯级相变储能系统放热性能的强化作用,对各级相变材料孔隙率梯度进行了深入研究,旨在提高系统整体换热性能,并得到以下结论。
(1)肋片在显热放热阶段强化传热作用更显著,而多孔介质在潜热放热阶段强化传热作用更显著。整个放热过程中,多孔介质比肋片的性能强化作用更明显。
(2)同时添加肋片和多孔介质时,梯级相变系统放热性能最优,PCM完全凝固时间缩短了40%。
(3)三种孔隙率梯度工况下,系统的放热效率无明显差异,但在负梯度孔隙率情况下,放热速率更高且更均匀。相比于正梯度孔隙率的情况,负梯度孔隙率具有更优的热性能。
符 号 说 明
C——比热容,J∕(kg·K)
H——焓值,J
L——相变材料的潜热,J∕kg
m——质量,kg
Q——热量,J
T——温度,K
V——速度,m∕s
β——相变材料的液相率
λ——热导率,W∕(m·K)
μ——动力黏度,Pa·s
ρ——密度,kg∕m3
ϕ——复合多孔相变材料孔隙率
下角标
f——传热流体
i——第i级相变储热器
in——入口边界
l——液态相变材料
out——出口边界
PCM——相变材料
s——固态相变材料
0——初始状态
